2.3设计轴对称图案 同步练习(含答案解析)
文档属性
| 名称 | 2.3设计轴对称图案 同步练习(含答案解析) | 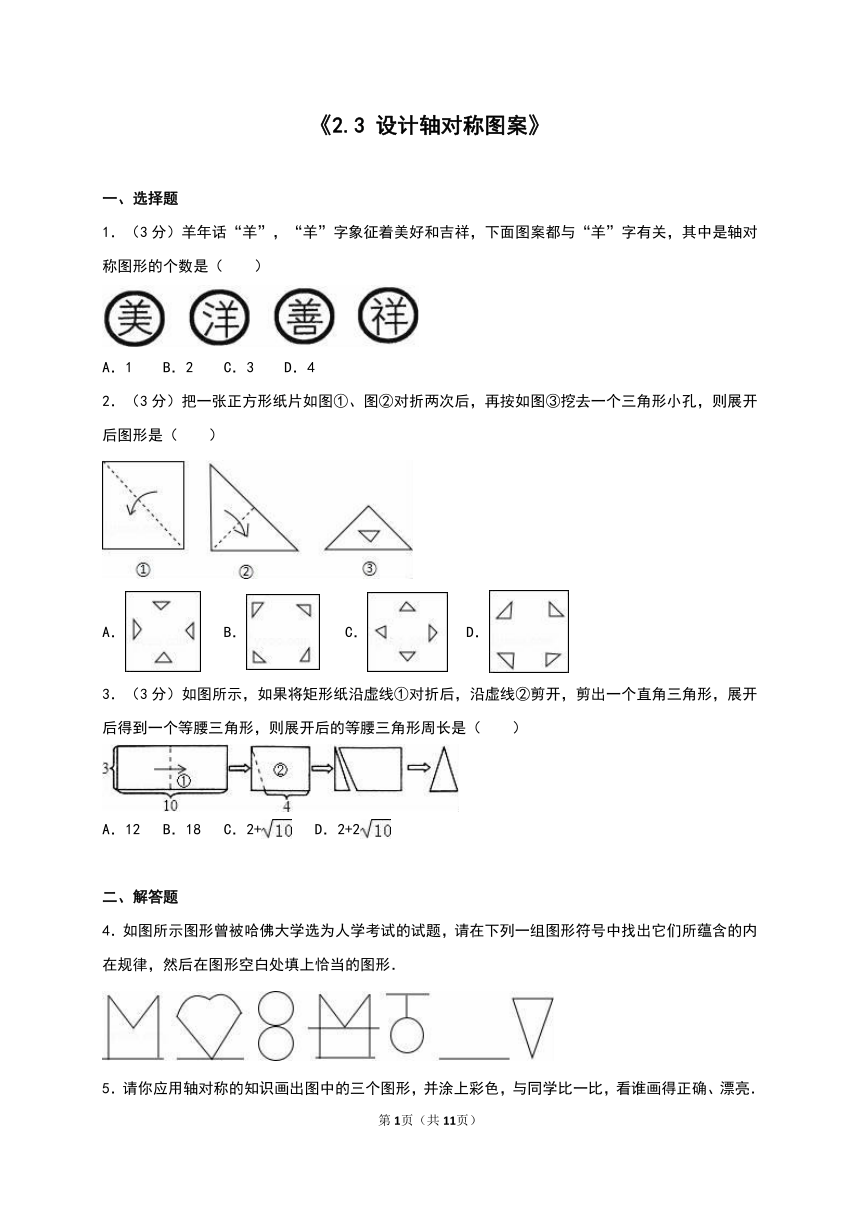 | |
| 格式 | zip | ||
| 文件大小 | 236.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-22 10:14:05 | ||
图片预览





文档简介
《2.3
设计轴对称图案》
一、选择题
1.(3分)羊年话“羊”,“羊”字象征着美好和吉祥,下面图案都与“羊”字有关,其中是轴对称图形的个数是( )
A.1
B.2
C.3
D.4
2.(3分)把一张正方形纸片如图①、图②对折两次后,再按如图③挖去一个三角形小孔,则展开后图形是( )
A.
B.
C.
D.
3.(3分)如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形,则展开后的等腰三角形周长是( )
A.12
B.18
C.2+
D.2+2
二、解答题
4.如图所示图形曾被哈佛大学选为人学考试的试题,请在下列一组图形符号中找出它们所蕴含的内在规律,然后在图形空白处填上恰当的图形.
5.请你应用轴对称的知识画出图中的三个图形,并涂上彩色,与同学比一比,看谁画得正确、漂亮.
6.用如图(1)所示的瓷砖拼成一个正方形,使拼成的图案成轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法.(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示)
7.以直线l为对称轴,画出图形的另一半.
8.利用如图设计出一个轴对称图案.
9.某居民小区搞绿化,要在一块矩形空地(如图)上建花坛,现征集设计方案,要求设计的图案由圆和正方形组成(圆与正方形的个数不限),并且使整个矩形场地成轴对称图形.请在如图矩形中画出你的设计方案.
10.如图的四个图案,都是轴对称图形,它们分别有着自己的含义,比如图(1)可以代表针织品、联通;图(2)可以代表法律、公正;图(3)可以代表航海、坚固;图(4)可以代表邮政、友谊等,请你自己也来设计一个轴对称图形,并请说明你所设计的轴对称图形的含义.
11.某市拟建造农民文化公园,将12个场馆排成6行,每行4个场馆,市政府将如图所示的设计图公布后,引起了一群初中生的浓厚兴趣,他们纷纷设计出许多精美的轴对称图形来,请你也设计一幅符合条件的图形.
12.仔细观察图(1)、图(2)、图(3)中阴影部分图案的共同特征,在图(4)、图(5)中再设计两幅具备上述特征的图案.(每小格面积为1)
13.如图,有两个7×4的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
(1)线段的一端点为梯形的顶点,另一个端点在梯形一边的格点上;
(2)将梯形分成两个图形,其中一个是轴对称图形;
(3)图1、图2中分成的轴对称图形不全等.
14.由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图).请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑,使它成为轴对称图形.
15.利用一条线段、一个圆、一个正三角形设计几个轴对称图案,并说明你要表达的意思.
《2.3
设计轴对称图案》
参考答案与试题解析
一、选择题
1.羊年话“羊”,“羊”字象征着美好和吉祥,下面图案都与“羊”字有关,其中是轴对称图形的个数是( )
A.1
B.2
C.3
D.4
【考点】轴对称图形.
【分析】根据轴对称图形的概念求解,看图形是不是关于直线对称.
【解答】解:美、善都是轴对称图形;而洋、祥都不是轴对称图形.
故选B.
【点评】轴对称图形的判断方法:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.
2.把一张正方形纸片如图①、图②对折两次后,再按如图③挖去一个三角形小孔,则展开后图形是( )
A.
B.
C.
D.
【考点】剪纸问题.
【专题】计算题.
【分析】结合空间思维,分析折叠的过程及剪三角形的位置,注意图形的对称性,易知展开的形状.
【解答】解:当正方形纸片两次沿对角线对折成为一直角三角形时,在直角三角形中间的位置上剪三角形,则直角顶点处完好,即原正方形中间无损,且三角形关于对角线对称,三角形的AB边平行于正方形的边.再结合C点位置可得答案为C.
故选C.
【点评】本题主要考查了学生的立体思维能力即操作能力.错误的主要原因是空间观念以及转化的能力不强,缺乏逻辑推理能力,需要在平时生活中多加培养.
3.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形,则展开后的等腰三角形周长是( )
A.12
B.18
C.2+
D.2+2
【考点】剪纸问题.
【分析】严格按照图的示意对折,裁剪后得到的是直角三角形,虚线①为矩形的对称轴,依据对称轴的性质虚线①平分矩形的长,即可得到沿虚线②裁下的直角三角形的短直角边为10÷2﹣4=1,虚线②为斜边,据勾股定理可得虚线②为,据等腰三角形底边的高平分底边的性质可以得到,展开后的等腰三角形的底边为2,故得到等腰三角形的周长.
【解答】解:根据题意,三角形的底边为2(10÷2﹣4)=2,腰的平方为32+12=10,
因此等腰三角形的腰为,
因此等腰三角形的周长为:2+2.
答:展开后等腰三角形的周长为2+2.
故选D.
【点评】本题主要考查了剪纸问题以及考查学生的动手能力和对相关性质的运用能力,只要亲自动手操作,答案就会很容易得出来.
二、解答题
4.如图所示图形曾被哈佛大学选为人学考试的试题,请在下列一组图形符号中找出它们所蕴含的内在规律,然后在图形空白处填上恰当的图形.
【考点】规律型:图形的变化类.
【分析】仔细观察会发现它们都是轴对称图形,所以在空白处再画一个轴对称图形即可.
【解答】解:从图中可以发现所有的图形都是轴对称图形,而且图形从左到右分别是1﹣7的数字,
所以画一个轴对称图形且数字为6即可.
故答案为:.
【点评】本题是一道规律型的题,首先要从图中找出规律,然后再根据规律画图.但还是考查了轴对称图形的性质.
5.请你应用轴对称的知识画出图中的三个图形,并涂上彩色,与同学比一比,看谁画得正确、漂亮.
【考点】利用轴对称设计图案.
【分析】根据轴对称图形的定义:沿一条直线折叠,直线两旁的部分能够互相重合的图形涂色即可.
【解答】解:如图所示:
.
【点评】此题主要考查了利用轴对称设计图案,关键是掌握轴对称图形的定义.
6.用如图(1)所示的瓷砖拼成一个正方形,使拼成的图案成轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法.(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示)
【考点】图形的剪拼;利用轴对称设计图案.
【分析】根据轴对称图形的法则去画即可,有多种图形.
【解答】解:(1)所作图形如下所示:
【点评】此题是图形的剪拼,主要考查学生对轴对称图形的理解以及操作能力.
7.以直线l为对称轴,画出图形的另一半.
【考点】作图-轴对称变换.
【分析】直接利用轴对称图形的性质得出对应点位置进而得出答案.
【解答】解:如图所示:
【点评】此题主要考查了作轴对称变换,正确得出对应点位置是解题关键.
8.利用如图设计出一个轴对称图案.
【考点】利用轴对称设计图案.
【分析】根据轴对称图形的定义:沿一条直线折叠,直线两旁的部分能够互相重合的图形涂色即可.
【解答】解:如图所示:
.
【点评】此题主要考查了利用轴对称设计图案,关键是掌握轴对称图形的定义.
9.某居民小区搞绿化,要在一块矩形空地(如图)上建花坛,现征集设计方案,要求设计的图案由圆和正方形组成(圆与正方形的个数不限),并且使整个矩形场地成轴对称图形.请在如图矩形中画出你的设计方案.
【考点】利用轴对称设计图案.
【专题】方案型;开放型.
【分析】根据轴对称图形的定义设计.即图形沿某一直线对折,图形能完全重合.
【解答】解:
【点评】本题主要考查了轴对称图形的性质.
10.如图的四个图案,都是轴对称图形,它们分别有着自己的含义,比如图(1)可以代表针织品、联通;图(2)可以代表法律、公正;图(3)可以代表航海、坚固;图(4)可以代表邮政、友谊等,请你自己也来设计一个轴对称图形,并请说明你所设计的轴对称图形的含义.
【考点】轴对称图形.
【分析】结合轴对称图形的概念进行解答即可.
【解答】解:.(答案不唯一).
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
11.某市拟建造农民文化公园,将12个场馆排成6行,每行4个场馆,市政府将如图所示的设计图公布后,引起了一群初中生的浓厚兴趣,他们纷纷设计出许多精美的轴对称图形来,请你也设计一幅符合条件的图形.
【考点】利用轴对称设计图案.
【分析】只要满足12个场馆排成6排,且形成的图形是轴对称图形即可.
【解答】解:如图所示:
.
【点评】本题考查了利用轴对称设计图案的知识,属于开放型题目,答案不唯一.
12.仔细观察图(1)、图(2)、图(3)中阴影部分图案的共同特征,在图(4)、图(5)中再设计两幅具备上述特征的图案.]
(答案不唯一)
【点评】本题考查轴对称图形的特点:沿某条直线折叠,直线两旁的部分能够互相重合.
14.由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图).请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑,使它成为轴对称图形.
【考点】利用轴对称设计图案.
【分析】根据轴对称图形的概念作图.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形.这条直线叫做对称轴,以16个相同的小正方形构成的大正方形的对称轴作出图形即可.
【解答】解:作图如下:
【点评】此题考查了轴对称图形和轴对称的作图方法.轴对称图形要找对称轴,轴对称要找关于对称轴对应的点.
15.利用一条线段、一个圆、一个正三角形设计几个轴对称图案,并说明你要表达的意思.
【考点】利用轴对称设计图案;等边三角形的性质.
【分析】根据轴对称轴图形的定义,画出图形即可.
【解答】解:如图所示,①表示劳动工具,②电灯泡,③路标.
【点评】本题考查对称轴图形的定义、等边三角形的性质等知识,解题的关键是理解题意,属于创新题目.
第4页(共12页)
设计轴对称图案》
一、选择题
1.(3分)羊年话“羊”,“羊”字象征着美好和吉祥,下面图案都与“羊”字有关,其中是轴对称图形的个数是( )
A.1
B.2
C.3
D.4
2.(3分)把一张正方形纸片如图①、图②对折两次后,再按如图③挖去一个三角形小孔,则展开后图形是( )
A.
B.
C.
D.
3.(3分)如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形,则展开后的等腰三角形周长是( )
A.12
B.18
C.2+
D.2+2
二、解答题
4.如图所示图形曾被哈佛大学选为人学考试的试题,请在下列一组图形符号中找出它们所蕴含的内在规律,然后在图形空白处填上恰当的图形.
5.请你应用轴对称的知识画出图中的三个图形,并涂上彩色,与同学比一比,看谁画得正确、漂亮.
6.用如图(1)所示的瓷砖拼成一个正方形,使拼成的图案成轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法.(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示)
7.以直线l为对称轴,画出图形的另一半.
8.利用如图设计出一个轴对称图案.
9.某居民小区搞绿化,要在一块矩形空地(如图)上建花坛,现征集设计方案,要求设计的图案由圆和正方形组成(圆与正方形的个数不限),并且使整个矩形场地成轴对称图形.请在如图矩形中画出你的设计方案.
10.如图的四个图案,都是轴对称图形,它们分别有着自己的含义,比如图(1)可以代表针织品、联通;图(2)可以代表法律、公正;图(3)可以代表航海、坚固;图(4)可以代表邮政、友谊等,请你自己也来设计一个轴对称图形,并请说明你所设计的轴对称图形的含义.
11.某市拟建造农民文化公园,将12个场馆排成6行,每行4个场馆,市政府将如图所示的设计图公布后,引起了一群初中生的浓厚兴趣,他们纷纷设计出许多精美的轴对称图形来,请你也设计一幅符合条件的图形.
12.仔细观察图(1)、图(2)、图(3)中阴影部分图案的共同特征,在图(4)、图(5)中再设计两幅具备上述特征的图案.(每小格面积为1)
13.如图,有两个7×4的网格,网格中每个小正方形的边长均为1,每个网格中各画有一个梯形.请在图1、图2中分别画出一条线段,同时满足以下要求:
(1)线段的一端点为梯形的顶点,另一个端点在梯形一边的格点上;
(2)将梯形分成两个图形,其中一个是轴对称图形;
(3)图1、图2中分成的轴对称图形不全等.
14.由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图).请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑,使它成为轴对称图形.
15.利用一条线段、一个圆、一个正三角形设计几个轴对称图案,并说明你要表达的意思.
《2.3
设计轴对称图案》
参考答案与试题解析
一、选择题
1.羊年话“羊”,“羊”字象征着美好和吉祥,下面图案都与“羊”字有关,其中是轴对称图形的个数是( )
A.1
B.2
C.3
D.4
【考点】轴对称图形.
【分析】根据轴对称图形的概念求解,看图形是不是关于直线对称.
【解答】解:美、善都是轴对称图形;而洋、祥都不是轴对称图形.
故选B.
【点评】轴对称图形的判断方法:如果一个图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形.
2.把一张正方形纸片如图①、图②对折两次后,再按如图③挖去一个三角形小孔,则展开后图形是( )
A.
B.
C.
D.
【考点】剪纸问题.
【专题】计算题.
【分析】结合空间思维,分析折叠的过程及剪三角形的位置,注意图形的对称性,易知展开的形状.
【解答】解:当正方形纸片两次沿对角线对折成为一直角三角形时,在直角三角形中间的位置上剪三角形,则直角顶点处完好,即原正方形中间无损,且三角形关于对角线对称,三角形的AB边平行于正方形的边.再结合C点位置可得答案为C.
故选C.
【点评】本题主要考查了学生的立体思维能力即操作能力.错误的主要原因是空间观念以及转化的能力不强,缺乏逻辑推理能力,需要在平时生活中多加培养.
3.如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形,则展开后的等腰三角形周长是( )
A.12
B.18
C.2+
D.2+2
【考点】剪纸问题.
【分析】严格按照图的示意对折,裁剪后得到的是直角三角形,虚线①为矩形的对称轴,依据对称轴的性质虚线①平分矩形的长,即可得到沿虚线②裁下的直角三角形的短直角边为10÷2﹣4=1,虚线②为斜边,据勾股定理可得虚线②为,据等腰三角形底边的高平分底边的性质可以得到,展开后的等腰三角形的底边为2,故得到等腰三角形的周长.
【解答】解:根据题意,三角形的底边为2(10÷2﹣4)=2,腰的平方为32+12=10,
因此等腰三角形的腰为,
因此等腰三角形的周长为:2+2.
答:展开后等腰三角形的周长为2+2.
故选D.
【点评】本题主要考查了剪纸问题以及考查学生的动手能力和对相关性质的运用能力,只要亲自动手操作,答案就会很容易得出来.
二、解答题
4.如图所示图形曾被哈佛大学选为人学考试的试题,请在下列一组图形符号中找出它们所蕴含的内在规律,然后在图形空白处填上恰当的图形.
【考点】规律型:图形的变化类.
【分析】仔细观察会发现它们都是轴对称图形,所以在空白处再画一个轴对称图形即可.
【解答】解:从图中可以发现所有的图形都是轴对称图形,而且图形从左到右分别是1﹣7的数字,
所以画一个轴对称图形且数字为6即可.
故答案为:.
【点评】本题是一道规律型的题,首先要从图中找出规律,然后再根据规律画图.但还是考查了轴对称图形的性质.
5.请你应用轴对称的知识画出图中的三个图形,并涂上彩色,与同学比一比,看谁画得正确、漂亮.
【考点】利用轴对称设计图案.
【分析】根据轴对称图形的定义:沿一条直线折叠,直线两旁的部分能够互相重合的图形涂色即可.
【解答】解:如图所示:
.
【点评】此题主要考查了利用轴对称设计图案,关键是掌握轴对称图形的定义.
6.用如图(1)所示的瓷砖拼成一个正方形,使拼成的图案成轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法.(要求三种拼法各不相同,所画图案中的阴影部分用斜线表示)
【考点】图形的剪拼;利用轴对称设计图案.
【分析】根据轴对称图形的法则去画即可,有多种图形.
【解答】解:(1)所作图形如下所示:
【点评】此题是图形的剪拼,主要考查学生对轴对称图形的理解以及操作能力.
7.以直线l为对称轴,画出图形的另一半.
【考点】作图-轴对称变换.
【分析】直接利用轴对称图形的性质得出对应点位置进而得出答案.
【解答】解:如图所示:
【点评】此题主要考查了作轴对称变换,正确得出对应点位置是解题关键.
8.利用如图设计出一个轴对称图案.
【考点】利用轴对称设计图案.
【分析】根据轴对称图形的定义:沿一条直线折叠,直线两旁的部分能够互相重合的图形涂色即可.
【解答】解:如图所示:
.
【点评】此题主要考查了利用轴对称设计图案,关键是掌握轴对称图形的定义.
9.某居民小区搞绿化,要在一块矩形空地(如图)上建花坛,现征集设计方案,要求设计的图案由圆和正方形组成(圆与正方形的个数不限),并且使整个矩形场地成轴对称图形.请在如图矩形中画出你的设计方案.
【考点】利用轴对称设计图案.
【专题】方案型;开放型.
【分析】根据轴对称图形的定义设计.即图形沿某一直线对折,图形能完全重合.
【解答】解:
【点评】本题主要考查了轴对称图形的性质.
10.如图的四个图案,都是轴对称图形,它们分别有着自己的含义,比如图(1)可以代表针织品、联通;图(2)可以代表法律、公正;图(3)可以代表航海、坚固;图(4)可以代表邮政、友谊等,请你自己也来设计一个轴对称图形,并请说明你所设计的轴对称图形的含义.
【考点】轴对称图形.
【分析】结合轴对称图形的概念进行解答即可.
【解答】解:.(答案不唯一).
【点评】本题考查了轴对称图形的概念,轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
11.某市拟建造农民文化公园,将12个场馆排成6行,每行4个场馆,市政府将如图所示的设计图公布后,引起了一群初中生的浓厚兴趣,他们纷纷设计出许多精美的轴对称图形来,请你也设计一幅符合条件的图形.
【考点】利用轴对称设计图案.
【分析】只要满足12个场馆排成6排,且形成的图形是轴对称图形即可.
【解答】解:如图所示:
.
【点评】本题考查了利用轴对称设计图案的知识,属于开放型题目,答案不唯一.
12.仔细观察图(1)、图(2)、图(3)中阴影部分图案的共同特征,在图(4)、图(5)中再设计两幅具备上述特征的图案.]
(答案不唯一)
【点评】本题考查轴对称图形的特点:沿某条直线折叠,直线两旁的部分能够互相重合.
14.由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑(如图).请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑,使它成为轴对称图形.
【考点】利用轴对称设计图案.
【分析】根据轴对称图形的概念作图.如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形.这条直线叫做对称轴,以16个相同的小正方形构成的大正方形的对称轴作出图形即可.
【解答】解:作图如下:
【点评】此题考查了轴对称图形和轴对称的作图方法.轴对称图形要找对称轴,轴对称要找关于对称轴对应的点.
15.利用一条线段、一个圆、一个正三角形设计几个轴对称图案,并说明你要表达的意思.
【考点】利用轴对称设计图案;等边三角形的性质.
【分析】根据轴对称轴图形的定义,画出图形即可.
【解答】解:如图所示,①表示劳动工具,②电灯泡,③路标.
【点评】本题考查对称轴图形的定义、等边三角形的性质等知识,解题的关键是理解题意,属于创新题目.
第4页(共12页)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
