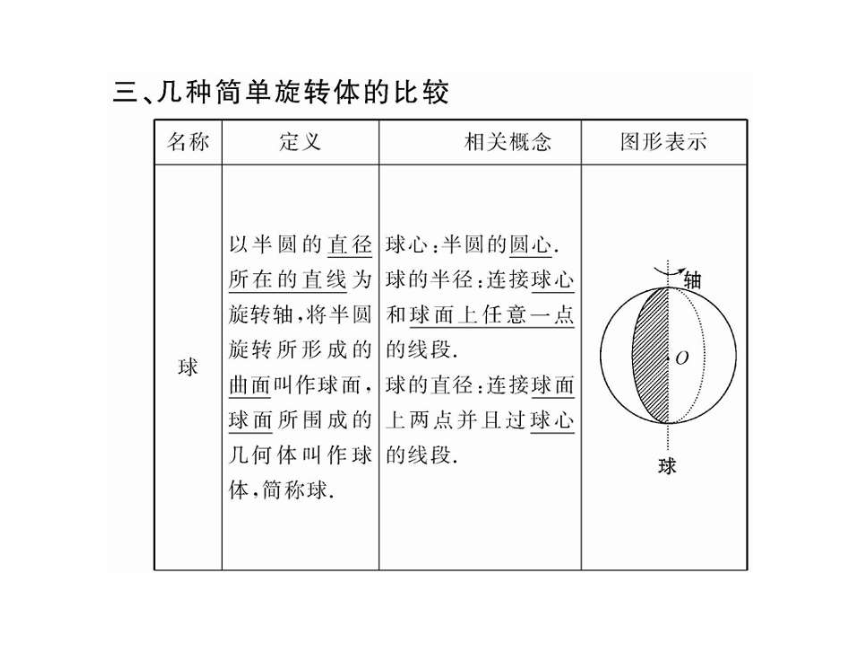
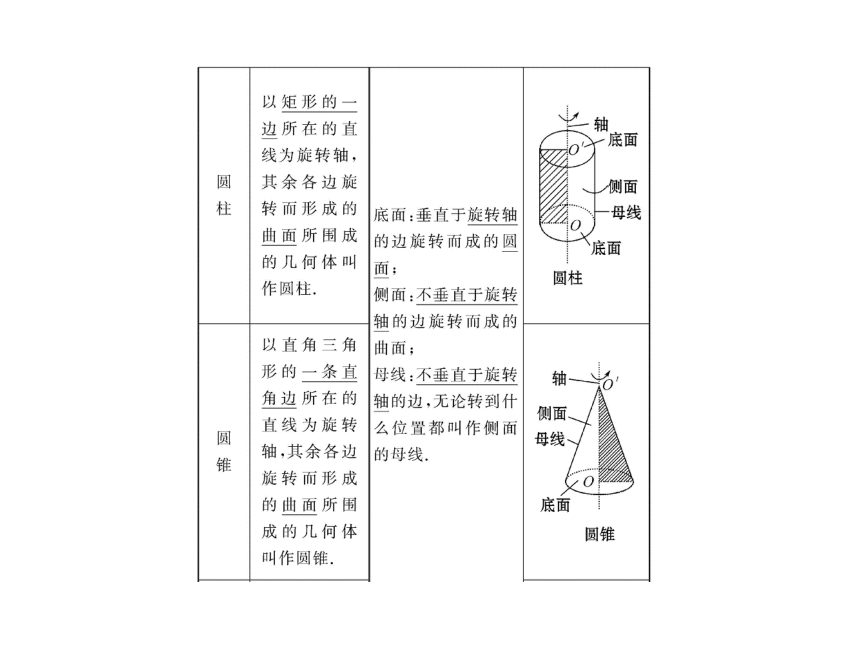
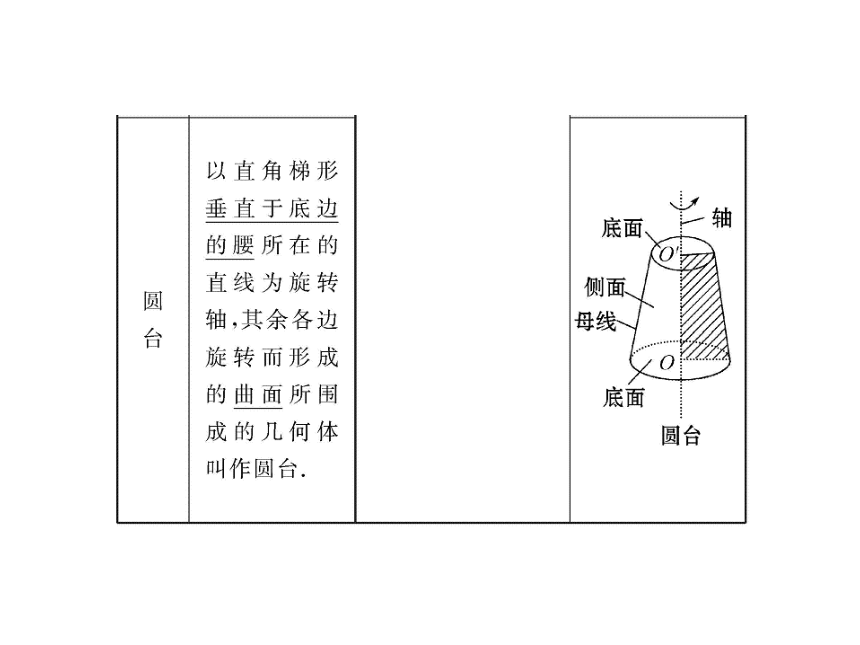
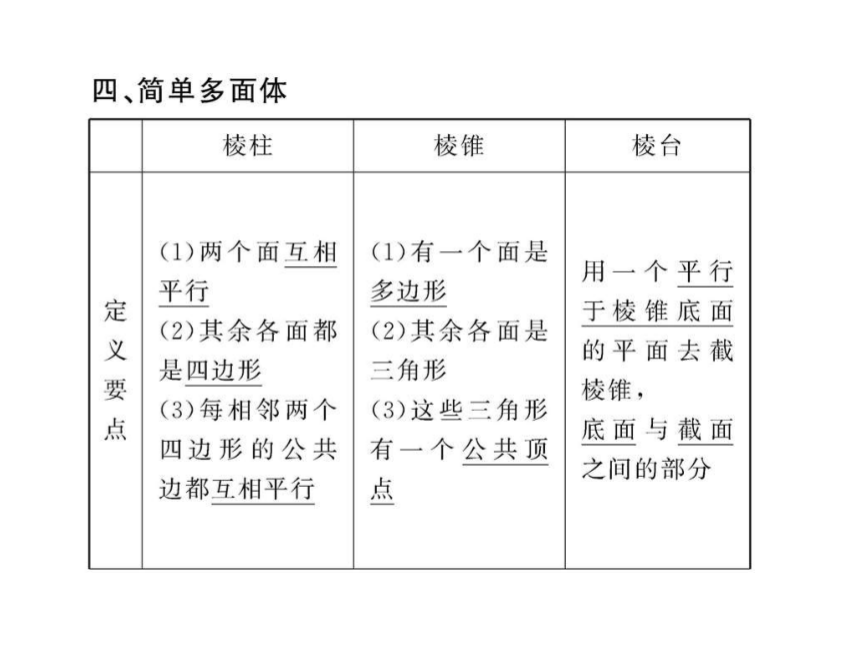
1.1 简单几何体 课件1
图片预览







文档简介
课件72张PPT。1.对简单旋转体形成过程的认识
(1)明确由哪个平面图形旋转而成.
(2)明确旋转轴是哪条直线.
(3)旋转必须形成封闭的曲面.简单旋转体的形成过程与性质2.注意简单旋转体的底面和截面的性质3.简单旋转体的轴截面的应用
(1)简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量.
(2)在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想. 【例1】下列说法中错误的是( )
(A)圆柱的轴截面是过母线的截面中面积最大的一个
(B)圆锥的轴截面是所有过顶点的截面中面积最大的一个
(C)圆台的所有平行于底面的截面都是圆面
(D)圆锥的所有轴截面都是全等的等腰三角形
【审题指导】本题中A、B较难判断,由于过圆柱母线的截面是矩形,过圆锥顶点的截面是三角形,可作图根据矩形、三角形面积的计算方法进行比较.【规范解答】选B.
A正确.如图①,A1B1>B1C1,而四边形ABB1A1和四边形BCC1B1
都是矩形,则
B错误.如图②,AB>BC,SO<SO′,∴△SAB的面积不一定比
△SBC的面积大.由轴截面特点知,C、D都正确.【变式训练】下列说法正确的是
( )
(A)平行于圆锥某一母线的截面是等腰三角形
(B)平行于圆台某一母线的截面是等腰梯形
(C)过圆锥顶点的截面是等腰三角形
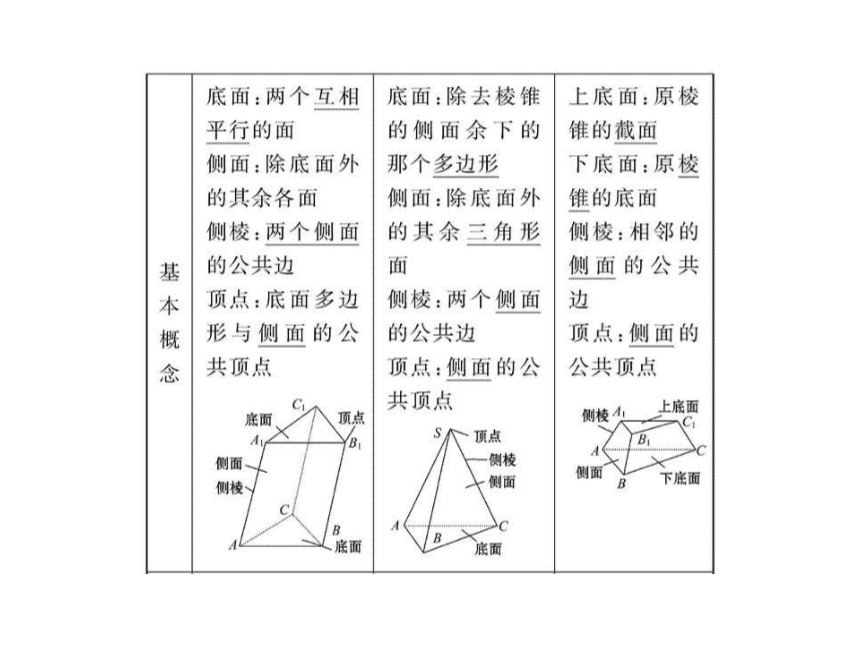
(D)过圆台上底面中心的截面是等腰梯形【解析】选C.只有当截面过圆锥的顶点时,所得三角形的两腰相等都是圆锥的母线,其余情况都可能不是等腰三角形.同理可知B、D错误.1.棱柱的结构特征
(1)底面:两个多边形全等且所在平面互相平行.
(2)侧面:都是平行四边形.
(3)侧棱:互相平行且相等.
(4)截面:
①平行于底面的截面是与底面全等的多边形.
②过不相邻的两条侧棱的截面是平行四边形.棱柱的结构特征2.特殊四棱柱之间的关系.
四棱柱是一类常见的简单多面体,正方体、长方体是特殊的四棱柱.它们之间的关系如图所示, 【例2】如图所示ABCD—A′B′C′D′
是长方体,当用平面BCFE把这个长方
体分成两部分后,各部分形成的多面
体还是棱柱吗?如果不是,请说明理
由;如果是,指出底面及侧棱.
【审题指导】判断多面体是否是棱柱,关键是寻找底面和侧面,并从这两个角度分析是否满足棱柱的定义,切忌只从摆放位置进行判断.【规范解答】截面BCFE右侧部分是棱柱,因为它满足棱柱的定义,它是三棱柱BEB′—CFC′,其中△BEB′和△CFC′是底面.EF,B′C′,BC是侧棱.截面BCFE左侧部分也是棱柱,它是四棱柱ABEA′—DCFD′,其中四边形ABEA′和四边形DCFD′是底面,A′D′,EF,BC,AD为侧棱.【变式训练】判断以下说法是否正确:
(1)有一个侧面是矩形的棱柱是直棱柱.
(2)棱柱的面中,至少有2个面互相平行.
(3)各侧面都是矩形的棱柱是长方体.
(4)一个n(n≥3)棱柱共有2n个顶点.
【解题提示】解答判断正误问题时,若要说明某种说法是错误的,只需举出一反例即可.而要说明某种说法是正确的,则需进行严格证明.【解析】(1)错误.反例如图所示三
棱柱ABC-A′B′C′中侧面BCC′B′
是矩形,但此三棱柱不是直棱柱.
(2)正确.棱柱的面中,至少有上
下两个底面平行,相对侧面也有
可能平行,如正六棱柱.(3)错误.例如直三棱柱各侧面都是矩形,但不是长方体.
(4)正确.棱柱的顶点是其底面多边形的顶点,n(n≥3)棱柱的底面是n边形有n个顶点,所以n(n≥3)棱柱上下两个底面共有2n个顶点.1.对几类特殊棱锥的认识
(1)三棱锥是面数最少的多面体,又称四面体.它的每一个面都可以作为底面.
(2)各棱都相等的四面体称为正四面体.
(3)正棱锥有以下性质:①侧面是全等的等腰三角形;②顶点与底面多边形中心的连线与底面垂直.棱锥、棱台的结构特征2.柱、锥、台之间的关系
在运动变化的观点下,柱、锥、台之间的关系可以用下图表示出来.
棱锥的侧棱所在的直线交于一点.【例3】判断以下说法是否正确:
(1)侧棱长都相等的棱锥是正棱锥.
(2)底面是正多边形,各侧面都是等腰三角形的棱锥是正棱锥.
(3)四面体的每一个面都可以作为棱锥的底面.
(4)棱锥的各侧棱长相等.
(5)正六棱锥的侧棱比底面正多边形的边长.
【审题指导】对于(1)(2)可根据正棱锥定义,从以下两个要点判断:①底面是正多边形;②各侧面全等.对于(3)要注意三棱锥也叫作四面体,对于(4)可举反例说明其错误.【规范解答】(1)错误.因为不知道底面是否为正多边形.
(2)错误.反例如图所示.
如图所示的三棱锥中有AB=AD=BD=BC=CD.
满足底面三角形BCD为等边三角形,三个
侧面△ABD,△ABC,△ACD都是等腰三角
形,但AC长度不定,三个侧面不一定全等.(3)正确.四面体是一个三棱锥,根据
棱锥的定义,三棱锥的每一个面都可
以作为底面.
(4)错误.棱锥的各侧棱长不一定相等.
如图所示四棱锥
P—ABCD各侧棱长不全相等.(5)正确.如图所示,正六棱锥中△OAB是等边三角形,OA=AB,△PAO是直角三角形,PA>OA,所以此说法正确.【互动探究】本例(1)改为“棱长都相等的三棱锥是正棱锥”正确吗?
【解析】正确.棱长都相等的三棱锥底面是正多边形,各侧面全等,是正三棱锥.【例】判断如图所示的几何体是不是台体,为什么?【审题指导】判断某几何体是否为台体,关键是看该几何体是否为相应的锥体用平行于底面的截面所截得的,否则不是台体.【规范解答】(1)(2)(3)不是台体,(1)中AA1,DD1相交于一点,而BB1,CC1交于另一点,不能还原成锥体,故不是台体.(2)中上、下两个底面不平行,故不是台体.(3)中⊙O与⊙O1不平行,故不是台体.(4)是一个台体.因为它是用平行于圆锥底面的平面截圆锥而得到的.【变式备选】判断如图所示几何体是不是棱台,为什么?
【解析】观察图形根据棱台的定义可以判断(2)(3)是棱台.(1)中几何体上下底面不平行故不是棱台.【典例】(12分)一个有30°角的直角三角板绕其各条边所在的直线旋转所得到的几何体是圆锥吗?如果以斜边上的高所在的直线为轴旋转180°得到什么图形?旋转360°又得到什么图形?
【审题指导】解题的关键是画出图形明确旋转轴的位置,借助常见简单旋转体的结构特征,判断旋转所得旋转体的形状.【规范解答】图(1)、(2)旋转一周得到的几何体是圆锥.
………………………………………………………4分
图(3)旋转一周所得几何体是两个圆锥拼接而成的几何体.
…………………………………………………… 8分
图(4)旋转180°是两个半圆锥的组合体;旋转360°,旋转轴左侧的直角三角形旋转得到的圆锥隐藏于右侧直角三角形旋转得到的圆锥内. …………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】如图,四边形ABCD为直
角梯形,分别以边AD、边AB、边CD所
在直线为旋转轴旋转,分析所形成的
三个几何体的结构特征.【解析】以边AD所在直线为旋转轴旋转,形成的几何体是圆台.如图以边AB所在直线为旋转轴旋转,形成的几何体是一个圆锥和一个圆柱拼接而成的几何体.如图以边CD所在直线为旋转轴旋转,形成的几何体是一个圆柱挖掉一个圆锥构成的几何体.如图1.将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )【解析】选C.由题意可知此直角梯形绕直线l旋转一周,得到圆台.2.下列几何体中是棱柱的有( )(A)②③⑤ (B)③⑤⑥
(C)②③④ (D)①③⑤
【解析】选D.根据棱柱的定义可知①③⑤是棱柱,与放置位置无关.3.四棱柱的顶点数、棱数、面数分别是( )
(A)8,12,6 (B)8,10,6
(C)6,9,5 (D)8,12,5
【解析】选A.根据四棱柱的结构特征可知四棱柱有8个顶点,12条棱,6个面.4.如图,将直角梯形ABCD绕AB边
所在的直线旋转一周,由此形成
的几何体是由____、_____等简单几何体构成的.
【解析】将直角梯形ABCD绕AB
边所在的直线旋转一周,形成
的几何体如图所示,是由圆
锥、圆柱构成的.
答案:圆锥 圆柱5.欣赏下列世博会场馆图片,结合所学知识说出这些建筑物主体部分给我们哪些几何体的形象?【解析】(1)主体部分为四棱台.
(2)有圆台、圆柱等.
(3)主体部分为三棱柱.
(4)主体部分为球.
(5)主体部分为圆台.
(6)主体部分为四棱柱.一、选择题(每题4分,共16分)
1.过正棱台两底面中心的截面一定是( )
(A)直角梯形 (B)等腰梯形
(C)一般梯形或等腰梯形 (D)矩形【解析】选C.如图所示,图(1)为一般梯形,图(2)为等腰梯形.2.下列关于棱柱的描述中,正确的是( )
(A)底面是正方形的四棱柱是正方体
(B)棱柱只有两个面互相平行
(C)棱柱所有的面都是平行四边形
(D)底面为六边形的棱柱是六棱柱【解析】选D.A错误,因为底面是正方形的四棱柱不一定是直棱柱,所以不一定是正方体.B错误,棱柱的侧面也有可能互相平行.C错误,棱柱的底面可以是任意多边形.根据棱柱的分类方式知D正确.3.下列说法正确的有( )
(1)在圆柱的上下底面圆周上各取一点,则这两点的连线是圆柱的母线;
(2)圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;
(3)在圆台上下底面的圆周上各取一点,则这两点的连线是圆台的母线;
(4)圆柱的任意两条母线所在的直线是互相平行的.
(A)1个 (B)2个 (C)3个 (D)4个【解析】选B.由圆柱、圆锥、圆台母线的定义可知(2)(4)正确.(1)(3)的反例如图所示.
【误区警示】解答本题时对圆台、圆柱母线的概念不清楚,容易导致错误.实际上圆台的母线可理解为:过圆台的上下底面圆的圆心的平面截圆台,这个平面和侧面的交线就是母线.圆柱的母线与此同理.4.若四棱柱的侧面是全等的矩形,则该棱柱是( )
(A)长方体 (B)正四棱柱
(C)正方体 (D)底面是菱形的直棱柱
【解析】选D.若四棱柱的侧面是全等的矩形,则可判定该四棱柱底面四条边相等,且侧棱垂直于底面,因此是底面为菱形的直棱柱.二、填空题(每题4分,共8分)
5.已知A={棱锥},B={正棱锥},C={正三棱锥},D={正四面体},写出这四个集合的包含关系_______(注:正四面体是各棱都相等的三棱锥)
【解析】正四面体各棱长都相等,各个面都是等边三角形,是特殊的正三棱锥.因此D C,至于A、B、C的关系则比较明显是C B A.
答案:D C B A6.已知长方体过同一个顶点的三个面的面积分别为
则它的体对角线长为__________.
【解析】设长方体的棱长分别为a,b,c,则
解之得 所以长方体的体对角线为
答案: 【方法技巧】巧化未知为已知
长方体棱长和体对角线长的关系公式为
此公式的推导利用了长方体中体对角线与棱构成的直角三
角形,体现了化立体几何问题为平面几何问题的思想方
法,这种思想方法对于解决立体几何问题是十分重要的.三、解答题(每题8分,共16分)
7.如图所示,AB⊥CD,CD∥AE,将五边形ABCDE绕AE所在的直线旋转一周,由此得到的几何体是由哪些几何体构成的?你能否画出这个几何体的大致形状? 【解题提示】解答本题应把握住AB⊥CD,CD∥AE, 这两个条件,同时应注意所围成的曲面的特征及简单旋转体的底面位置.
【解析】此几何体自上而
下依次为圆台、圆柱、圆锥.
如图所示8. 根据棱柱的结构特征思考以下三个问题:
(1)正六棱柱有多少对平行平面?能作为棱柱底面的有几对?
(2)棱柱的任何两个平行平面都可以作为棱柱的底面吗?
(3)不在同一个面上的两个顶点的连线叫作棱柱的体对角线.试写出正六棱柱ABCDEF-A′B′C′D′E′F′的体对角线.【解析】(1)如图所示,正六棱柱有四
对平行平面,其中只有一对可以作为
棱柱底面.
(2)由(1)知不是棱柱的任何两个平行平
面都可以作为棱柱的底面.
(3)如图所示,正六棱柱的体对角线有AC′,AD′,AE′, BD′,BE′,BF′,CE′,CF′,CA′,DF′,DA′,DB′, EA′,EB′,EC′,FB′,FC′,FD′,共有18条.【挑战能力】
(10分)在正四棱柱上任意选择4个顶点,试画图分析以下两个问题:
(1)这4个顶点可能是哪几种平面图形的顶点?
(2)这4个顶点可能是哪几种空间图形的顶点?【解析】(1)这4个顶点可能是以下平面图形的顶点:矩形;正方形.
(2)这4个顶点可能是以下空间图形的顶点:
有三个面为直角三角形,有一个面为等腰三角形其余面是直角三角形的四面体(如图1、2);每个面都是等腰三角形的四面体(如图3);每个面都是直角三角形的四面体(如图4).
(1)明确由哪个平面图形旋转而成.
(2)明确旋转轴是哪条直线.
(3)旋转必须形成封闭的曲面.简单旋转体的形成过程与性质2.注意简单旋转体的底面和截面的性质3.简单旋转体的轴截面的应用
(1)简单旋转体的轴截面中有底面半径、母线、高等体现简单旋转体结构特征的关键量.
(2)在轴截面中解决简单旋转体问题体现了化空间图形为平面图形的转化思想. 【例1】下列说法中错误的是( )
(A)圆柱的轴截面是过母线的截面中面积最大的一个
(B)圆锥的轴截面是所有过顶点的截面中面积最大的一个
(C)圆台的所有平行于底面的截面都是圆面
(D)圆锥的所有轴截面都是全等的等腰三角形
【审题指导】本题中A、B较难判断,由于过圆柱母线的截面是矩形,过圆锥顶点的截面是三角形,可作图根据矩形、三角形面积的计算方法进行比较.【规范解答】选B.
A正确.如图①,A1B1>B1C1,而四边形ABB1A1和四边形BCC1B1
都是矩形,则
B错误.如图②,AB>BC,SO<SO′,∴△SAB的面积不一定比
△SBC的面积大.由轴截面特点知,C、D都正确.【变式训练】下列说法正确的是
( )
(A)平行于圆锥某一母线的截面是等腰三角形
(B)平行于圆台某一母线的截面是等腰梯形
(C)过圆锥顶点的截面是等腰三角形
(D)过圆台上底面中心的截面是等腰梯形【解析】选C.只有当截面过圆锥的顶点时,所得三角形的两腰相等都是圆锥的母线,其余情况都可能不是等腰三角形.同理可知B、D错误.1.棱柱的结构特征
(1)底面:两个多边形全等且所在平面互相平行.
(2)侧面:都是平行四边形.
(3)侧棱:互相平行且相等.
(4)截面:
①平行于底面的截面是与底面全等的多边形.
②过不相邻的两条侧棱的截面是平行四边形.棱柱的结构特征2.特殊四棱柱之间的关系.
四棱柱是一类常见的简单多面体,正方体、长方体是特殊的四棱柱.它们之间的关系如图所示, 【例2】如图所示ABCD—A′B′C′D′
是长方体,当用平面BCFE把这个长方
体分成两部分后,各部分形成的多面
体还是棱柱吗?如果不是,请说明理
由;如果是,指出底面及侧棱.
【审题指导】判断多面体是否是棱柱,关键是寻找底面和侧面,并从这两个角度分析是否满足棱柱的定义,切忌只从摆放位置进行判断.【规范解答】截面BCFE右侧部分是棱柱,因为它满足棱柱的定义,它是三棱柱BEB′—CFC′,其中△BEB′和△CFC′是底面.EF,B′C′,BC是侧棱.截面BCFE左侧部分也是棱柱,它是四棱柱ABEA′—DCFD′,其中四边形ABEA′和四边形DCFD′是底面,A′D′,EF,BC,AD为侧棱.【变式训练】判断以下说法是否正确:
(1)有一个侧面是矩形的棱柱是直棱柱.
(2)棱柱的面中,至少有2个面互相平行.
(3)各侧面都是矩形的棱柱是长方体.
(4)一个n(n≥3)棱柱共有2n个顶点.
【解题提示】解答判断正误问题时,若要说明某种说法是错误的,只需举出一反例即可.而要说明某种说法是正确的,则需进行严格证明.【解析】(1)错误.反例如图所示三
棱柱ABC-A′B′C′中侧面BCC′B′
是矩形,但此三棱柱不是直棱柱.
(2)正确.棱柱的面中,至少有上
下两个底面平行,相对侧面也有
可能平行,如正六棱柱.(3)错误.例如直三棱柱各侧面都是矩形,但不是长方体.
(4)正确.棱柱的顶点是其底面多边形的顶点,n(n≥3)棱柱的底面是n边形有n个顶点,所以n(n≥3)棱柱上下两个底面共有2n个顶点.1.对几类特殊棱锥的认识
(1)三棱锥是面数最少的多面体,又称四面体.它的每一个面都可以作为底面.
(2)各棱都相等的四面体称为正四面体.
(3)正棱锥有以下性质:①侧面是全等的等腰三角形;②顶点与底面多边形中心的连线与底面垂直.棱锥、棱台的结构特征2.柱、锥、台之间的关系
在运动变化的观点下,柱、锥、台之间的关系可以用下图表示出来.
棱锥的侧棱所在的直线交于一点.【例3】判断以下说法是否正确:
(1)侧棱长都相等的棱锥是正棱锥.
(2)底面是正多边形,各侧面都是等腰三角形的棱锥是正棱锥.
(3)四面体的每一个面都可以作为棱锥的底面.
(4)棱锥的各侧棱长相等.
(5)正六棱锥的侧棱比底面正多边形的边长.
【审题指导】对于(1)(2)可根据正棱锥定义,从以下两个要点判断:①底面是正多边形;②各侧面全等.对于(3)要注意三棱锥也叫作四面体,对于(4)可举反例说明其错误.【规范解答】(1)错误.因为不知道底面是否为正多边形.
(2)错误.反例如图所示.
如图所示的三棱锥中有AB=AD=BD=BC=CD.
满足底面三角形BCD为等边三角形,三个
侧面△ABD,△ABC,△ACD都是等腰三角
形,但AC长度不定,三个侧面不一定全等.(3)正确.四面体是一个三棱锥,根据
棱锥的定义,三棱锥的每一个面都可
以作为底面.
(4)错误.棱锥的各侧棱长不一定相等.
如图所示四棱锥
P—ABCD各侧棱长不全相等.(5)正确.如图所示,正六棱锥中△OAB是等边三角形,OA=AB,△PAO是直角三角形,PA>OA,所以此说法正确.【互动探究】本例(1)改为“棱长都相等的三棱锥是正棱锥”正确吗?
【解析】正确.棱长都相等的三棱锥底面是正多边形,各侧面全等,是正三棱锥.【例】判断如图所示的几何体是不是台体,为什么?【审题指导】判断某几何体是否为台体,关键是看该几何体是否为相应的锥体用平行于底面的截面所截得的,否则不是台体.【规范解答】(1)(2)(3)不是台体,(1)中AA1,DD1相交于一点,而BB1,CC1交于另一点,不能还原成锥体,故不是台体.(2)中上、下两个底面不平行,故不是台体.(3)中⊙O与⊙O1不平行,故不是台体.(4)是一个台体.因为它是用平行于圆锥底面的平面截圆锥而得到的.【变式备选】判断如图所示几何体是不是棱台,为什么?
【解析】观察图形根据棱台的定义可以判断(2)(3)是棱台.(1)中几何体上下底面不平行故不是棱台.【典例】(12分)一个有30°角的直角三角板绕其各条边所在的直线旋转所得到的几何体是圆锥吗?如果以斜边上的高所在的直线为轴旋转180°得到什么图形?旋转360°又得到什么图形?
【审题指导】解题的关键是画出图形明确旋转轴的位置,借助常见简单旋转体的结构特征,判断旋转所得旋转体的形状.【规范解答】图(1)、(2)旋转一周得到的几何体是圆锥.
………………………………………………………4分
图(3)旋转一周所得几何体是两个圆锥拼接而成的几何体.
…………………………………………………… 8分
图(4)旋转180°是两个半圆锥的组合体;旋转360°,旋转轴左侧的直角三角形旋转得到的圆锥隐藏于右侧直角三角形旋转得到的圆锥内. …………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】如图,四边形ABCD为直
角梯形,分别以边AD、边AB、边CD所
在直线为旋转轴旋转,分析所形成的
三个几何体的结构特征.【解析】以边AD所在直线为旋转轴旋转,形成的几何体是圆台.如图以边AB所在直线为旋转轴旋转,形成的几何体是一个圆锥和一个圆柱拼接而成的几何体.如图以边CD所在直线为旋转轴旋转,形成的几何体是一个圆柱挖掉一个圆锥构成的几何体.如图1.将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )【解析】选C.由题意可知此直角梯形绕直线l旋转一周,得到圆台.2.下列几何体中是棱柱的有( )(A)②③⑤ (B)③⑤⑥
(C)②③④ (D)①③⑤
【解析】选D.根据棱柱的定义可知①③⑤是棱柱,与放置位置无关.3.四棱柱的顶点数、棱数、面数分别是( )
(A)8,12,6 (B)8,10,6
(C)6,9,5 (D)8,12,5
【解析】选A.根据四棱柱的结构特征可知四棱柱有8个顶点,12条棱,6个面.4.如图,将直角梯形ABCD绕AB边
所在的直线旋转一周,由此形成
的几何体是由____、_____等简单几何体构成的.
【解析】将直角梯形ABCD绕AB
边所在的直线旋转一周,形成
的几何体如图所示,是由圆
锥、圆柱构成的.
答案:圆锥 圆柱5.欣赏下列世博会场馆图片,结合所学知识说出这些建筑物主体部分给我们哪些几何体的形象?【解析】(1)主体部分为四棱台.
(2)有圆台、圆柱等.
(3)主体部分为三棱柱.
(4)主体部分为球.
(5)主体部分为圆台.
(6)主体部分为四棱柱.一、选择题(每题4分,共16分)
1.过正棱台两底面中心的截面一定是( )
(A)直角梯形 (B)等腰梯形
(C)一般梯形或等腰梯形 (D)矩形【解析】选C.如图所示,图(1)为一般梯形,图(2)为等腰梯形.2.下列关于棱柱的描述中,正确的是( )
(A)底面是正方形的四棱柱是正方体
(B)棱柱只有两个面互相平行
(C)棱柱所有的面都是平行四边形
(D)底面为六边形的棱柱是六棱柱【解析】选D.A错误,因为底面是正方形的四棱柱不一定是直棱柱,所以不一定是正方体.B错误,棱柱的侧面也有可能互相平行.C错误,棱柱的底面可以是任意多边形.根据棱柱的分类方式知D正确.3.下列说法正确的有( )
(1)在圆柱的上下底面圆周上各取一点,则这两点的连线是圆柱的母线;
(2)圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;
(3)在圆台上下底面的圆周上各取一点,则这两点的连线是圆台的母线;
(4)圆柱的任意两条母线所在的直线是互相平行的.
(A)1个 (B)2个 (C)3个 (D)4个【解析】选B.由圆柱、圆锥、圆台母线的定义可知(2)(4)正确.(1)(3)的反例如图所示.
【误区警示】解答本题时对圆台、圆柱母线的概念不清楚,容易导致错误.实际上圆台的母线可理解为:过圆台的上下底面圆的圆心的平面截圆台,这个平面和侧面的交线就是母线.圆柱的母线与此同理.4.若四棱柱的侧面是全等的矩形,则该棱柱是( )
(A)长方体 (B)正四棱柱
(C)正方体 (D)底面是菱形的直棱柱
【解析】选D.若四棱柱的侧面是全等的矩形,则可判定该四棱柱底面四条边相等,且侧棱垂直于底面,因此是底面为菱形的直棱柱.二、填空题(每题4分,共8分)
5.已知A={棱锥},B={正棱锥},C={正三棱锥},D={正四面体},写出这四个集合的包含关系_______(注:正四面体是各棱都相等的三棱锥)
【解析】正四面体各棱长都相等,各个面都是等边三角形,是特殊的正三棱锥.因此D C,至于A、B、C的关系则比较明显是C B A.
答案:D C B A6.已知长方体过同一个顶点的三个面的面积分别为
则它的体对角线长为__________.
【解析】设长方体的棱长分别为a,b,c,则
解之得 所以长方体的体对角线为
答案: 【方法技巧】巧化未知为已知
长方体棱长和体对角线长的关系公式为
此公式的推导利用了长方体中体对角线与棱构成的直角三
角形,体现了化立体几何问题为平面几何问题的思想方
法,这种思想方法对于解决立体几何问题是十分重要的.三、解答题(每题8分,共16分)
7.如图所示,AB⊥CD,CD∥AE,将五边形ABCDE绕AE所在的直线旋转一周,由此得到的几何体是由哪些几何体构成的?你能否画出这个几何体的大致形状? 【解题提示】解答本题应把握住AB⊥CD,CD∥AE, 这两个条件,同时应注意所围成的曲面的特征及简单旋转体的底面位置.
【解析】此几何体自上而
下依次为圆台、圆柱、圆锥.
如图所示8. 根据棱柱的结构特征思考以下三个问题:
(1)正六棱柱有多少对平行平面?能作为棱柱底面的有几对?
(2)棱柱的任何两个平行平面都可以作为棱柱的底面吗?
(3)不在同一个面上的两个顶点的连线叫作棱柱的体对角线.试写出正六棱柱ABCDEF-A′B′C′D′E′F′的体对角线.【解析】(1)如图所示,正六棱柱有四
对平行平面,其中只有一对可以作为
棱柱底面.
(2)由(1)知不是棱柱的任何两个平行平
面都可以作为棱柱的底面.
(3)如图所示,正六棱柱的体对角线有AC′,AD′,AE′, BD′,BE′,BF′,CE′,CF′,CA′,DF′,DA′,DB′, EA′,EB′,EC′,FB′,FC′,FD′,共有18条.【挑战能力】
(10分)在正四棱柱上任意选择4个顶点,试画图分析以下两个问题:
(1)这4个顶点可能是哪几种平面图形的顶点?
(2)这4个顶点可能是哪几种空间图形的顶点?【解析】(1)这4个顶点可能是以下平面图形的顶点:矩形;正方形.
(2)这4个顶点可能是以下空间图形的顶点:
有三个面为直角三角形,有一个面为等腰三角形其余面是直角三角形的四面体(如图1、2);每个面都是等腰三角形的四面体(如图3);每个面都是直角三角形的四面体(如图4).
