1.2 直观图 课件1
图片预览










文档简介
课件73张PPT。1.2 直观图 斜二测画法的作图技巧
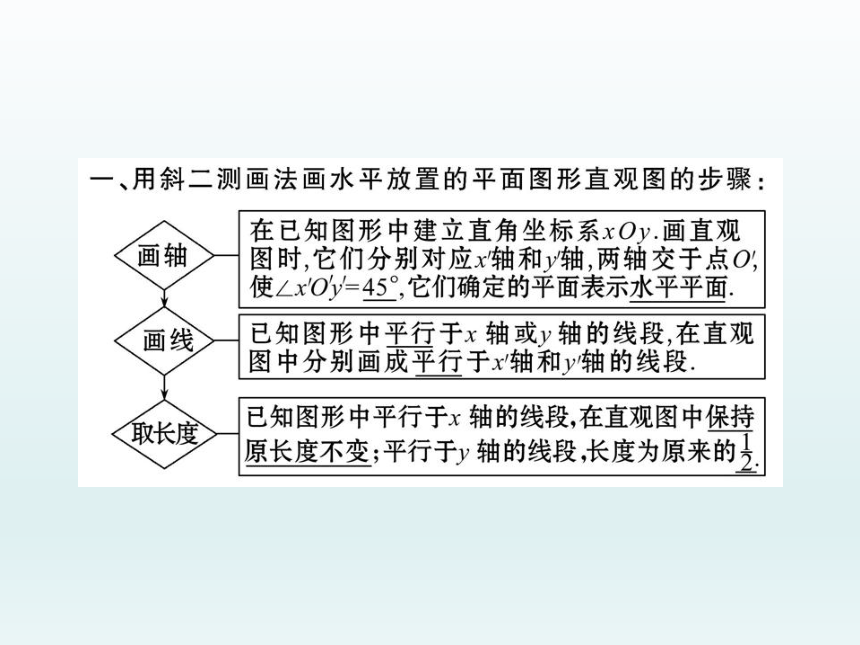
1.建立直角坐标系时,要让原平面图形的顶点尽可能多地落在坐标轴或与坐标轴平行的线段上.
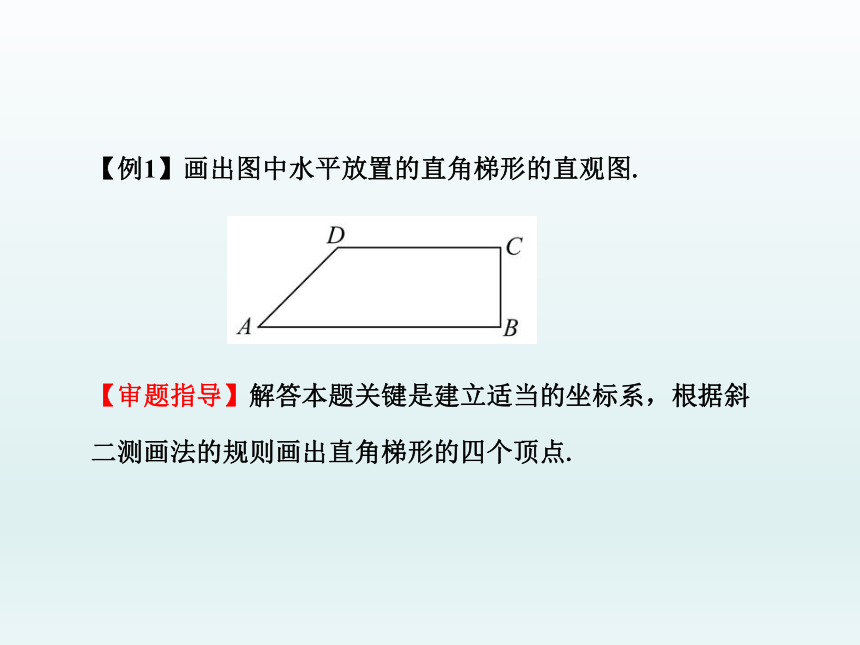
2.原图中不与x轴或y轴平行的线段,可以先作坐标轴的平行线为辅助线画出其端点,然后再连线.画水平放置的平面图形的直观图 水平放置的平面图形的直观图与原图形相比,平行关系是不变的,角的大小,线线垂直关系等都有可能变化.【例1】画出图中水平放置的直角梯形的直观图.
【审题指导】解答本题关键是建立适当的坐标系,根据斜二测画法的规则画出直角梯形的四个顶点.【规范解答】画法:
(1)在已知图形(直角梯形)所在平面上建立平面直角坐标系xOy.另选平面画直观图,先画x′轴和y′轴,使∠x′O′y′=45°.(2)将已知图形中平行于x轴或平行于y轴的线段在直观图中
分别画成平行于x′轴或平行于y′轴的线段,且已知图形
中平行于x轴的线段在直观图中保持原长度不变;平行于y
轴的线段,在直观图中长度为原来的(3)连线成图(擦去辅助线).【变式训练】画出图中四边形OABC的直观图(图中数据已给出).【解析】以O为原点,OB所在直线为x轴建立直角坐标系xOy,如图甲,如图乙,作∠x′O′y′=45°,其中O′B′=4,O′D′=3,
O′C′=1,过点D′作∠B′D′A′=135°,
使A′D′=1,顺次连接O′A′,A′B′,B′C′,擦去辅助线,所得四边形O′A′B′C′即为四边形OABC的直观图.【误区警示】解答本题容易在确定点A在直观图中的位置时
出错,出错原因一是不能根据AD∥y轴,通过画A′D′确定
点A′,二是忽视了1.画棱柱、棱锥的直观图可分以下四步:
(1)画轴:通常以高所在直线为z轴建系.
(2)画底面:根据平面图形的直观图画法确定底面.
(3)确定顶点:利用与z轴平行或在z轴上的线段确定有关顶点.
(4)连线成图.画立体图形的直观图2.画棱台的直观图可分以下四步:
(1)画轴:通常以高所在直线为z轴建系.
(2)画下底面.
(3)画高,画上底面.
(4)连线成图.
要注意最后对图形的修正:一要擦去辅助线,二要把被遮线画虚线.【例2】已知三棱锥P-ABC中PA与底面ABC垂直,四个面都
是直角三角形,且∠PAC=∠PAB=∠PBC=∠ABC=90°,
PA=1,AC=2, 试画此三棱锥的直观图.
【审题指导】解题的关键在于寻找此三棱锥的高,并以高所在的直线为z轴建系,画出底面的直观图,确定顶点P,连线成图.【规范解答】(1)画底面.(根据平面图形的直观图的画法)(如图1)(2)画z′轴(z′轴与x′轴的夹角为90°),并画高(即PA与原长相等),连线成图.(如图2)(3)擦去辅助线,被遮线画虚线.(如图3)【互动探究】本例中条件“已知三棱锥P-ABC中PA与底面ABC垂直,PA=1,AC=2”不变,其它条件改为“且∠PAC= ∠PAB=∠BAC=90°,AB=2”,则如何画此几何体的直观图.
【解题提示】解题时只要注意PA、AB、AC两两垂直,就可以建立恰当的坐标系画出直观图.【解析】(1)画底面.(根据平面图形的直观图的画法) (如图1)(2)画z′轴(z′轴与x′轴的交角为90°),并画高(即PA与原长相等),连线成图.(如图2)(3)擦去辅助线,被遮线画虚线.(如图3) 在斜二测画法中,直观图与原图的关系
(1)平行性不变.原图中互相平行的直线在直观图中仍然互相平行.
(2)共点、共线性不变.原图中相交于一点的直线,在直观图中仍然交于一点.原图中在一条直线上的点,在直观图中仍然在同一条直线上.
(3)平行线段的长度比不变.平面图形的直观图与原图形之间的关系 直观图的形状与原图相比有很大的变化,因此要借助斜二测画法的原理和有关公理定理,推断出原图的形状和性质,而不能只凭观察.【例3】在水平放置的平面α内有一边长为1的正
方形A′B′C′D′,如图,其中对角线A′C′水
平放置.已知该正方形是某个四边形用斜二测画
法画出的直观图,试画出该四边形的原图并求面积.
【审题指导】根据斜二测画法进行逆向思维,画出原图,再根据图中线的关系求面积.【规范解答】四边形ABCD的原图形如图所示.
∵A′C′水平放置,A′B′C′D′为正方形,
∴在四边形ABCD中,DA⊥AC.
∵DA=2D′A′=2,【变式训练】如图是△ABC利用斜二测画法得到的水平放置的直观图△A′B′C′,其中A′B′∥y′轴,B′C′∥x′轴,若△A′B′C′的面积是3,求△ABC的面积.【解析】由题意知△ABC为直角三角形,且AB⊥BC.
由斜二测画法的原理知AB=2A′B′,BC=B′C′,
又【例】如图所示,A′B′C′D′是
一个水平放置的平面图形的斜二测
直观图,已知A′B′C′D′是一个
直角梯形,A′B′∥C′D′,A′D′⊥C′D′且B′C′与y′轴平行,又A′B′=6,D′C′=4,A′D′=2,试求原图形ABCD的面积.【审题指导】解答本题的关键是首先根据斜二测画法的原理,判断出BC⊥AB,并计算线段BC、DC、AB的长度,然后再求原图形ABCD的面积.【规范解答】如图,由斜二测画法的原理知梯形A′B′C′D′的原图形ABCD为梯形,且BC⊥AB.
∵AB=A′B′=6,DC=D′C′=4,【变式备选】如图所示,△A′B′C′是水平放置的平面图形的斜二测直观图,将其恢复成原图形.【解析】画法:(1)画直角坐标系xOy,如图(2)所示,在x轴上取OA=O′A′,即CA=C′A′;
(2)在图(1)中,过B′作B′D′∥y′轴,交x′轴于D′,在x轴上取OD=O′D′,过D作DB∥y轴,并使DB=2D′B′.
(3)连接AB、BC,擦去辅助线,则△ABC即为△A′B′C′原来的图形,如图所示.【典例】(12分)已知等边三角形ABC的边长为a,试求△ABC的边AB水平放置时的直观图△A′B′C′的面积.
【审题指导】根据题目条件画出等边三角形ABC的实际图形和直观图,重点是分析底边长和高的变化情况.【规范解答】如图所示,作出等边三角形ABC的实际图形和直观图. …………………………………………………4分由图可知,A′B′=AB=a,………………………………6分
……………………………………8分
在图(2)中,作C′D′⊥A′B′于D′,
则 ………………………………10分
…………………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】等腰梯形ABCD中,上底边CD=1,
下底边AB=3,按平行于上、下底边取x轴,求该等腰梯形的直观图A′B′C′D′的面积.
【解析】等腰梯形ABCD的高为1,而直观图A′B′C′D′仍
为梯形,其高为 故面积为1.下面的说法正确的是( )
(A)水平放置的正方形的直观图可能是梯形
(B)两条相交的直线的直观图可能是平行直线
(C)互相垂直的两条直线的直观图仍然互相垂直
(D)水平放置的平行四边形的直观图仍是平行四边形
【解析】选D.水平放置的平面图形的直观图与原图形相比,平行关系是不变的,角的大小、线线垂直关系等都有可能变化,故选D.2.如图是用斜二测画法画某个图形
ABCDE的水平放置的直观图,则对
原图ABCDE,说法错误的是( )
(A)原图形ABCDE中∠CBA是直角
(B)原图形ABCDE中ED∥AB
(C)原图形ABCDE中∠EAB是直角
(D)原图形ABCDE中ED的长度小于AB的长度
【解析】选A.直观图中∠C′B′A′是直角,还原为原图形后是锐角,故错误.3.给出下列说法:
①水平放置的角的直观图一定是角;
②相等的角在直观图中仍相等;
③长度相等的线段在直观图中仍相等;
④如果一个三角形不是等腰三角形,那么该三角形水平放置的直观图一定不是等腰三角形.
其中叙述正确的个数是___________.【解析】水平放置的正方形的直观图是邻边不等的平行四边形,知②③错误.④错误.如下图所示Rt△OAB中OB=2OA, ∠AOB=90°,不是等腰三角形,但是该三角形水平放置的直观图是△O′A′B′,其中O′A′=O′B′是等腰三角形.
答案:14.如图为水平放置的正方形ABCO,它在直角坐标系xOy中点B的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为___________.【解析】
B′到x′轴的距离为
答案: 5.画如图放置的直角三角形的直观图.【解析】画法:(1)画x′轴和y′轴,使∠x′O′y′=45°.
(2)在原图中作BD⊥x轴,垂足为D.
(3)截取O′A′=OA,
O′D′=OD, 且B′D′∥y′轴.
(4)连线成图.(擦去辅助线)一、选择题(每题4分,共16分)
1.利用斜二测画法得到:①三角形的水平放置的直观图是三角形;②平行四边形的水平放置的直观图是平行四边形;③正方形的水平放置的直观图是正方形;④菱形的水平放置的直观图是菱形.以上结论正确的是( )
(A)①② (B)①
(C)③④ (D)①②③④【解析】选A.水平放置的平面图形的直观图与原图形相比,角的大小、线线垂直关系、线段的长度等都有可能变化,故③④错误.2如图,用斜二测画法
画一个水平放置的平面图形的直观图为一个正
方形,则原来图形的形状是( ) 【解题提示】先计算直观图中坐标轴上线段的长度,再根据斜二测画法的原则,从长度和平行关系两个方面判断,选出正确答案.
【解析】选A.根据斜二测画法知,在y轴上的线段长度为直观图中长度的2倍,可知A正确.3.如图,
Rt△O′A′B′是一平面图形的直观
图,直角边O′B′=1,则这个平面
图形的原图形的面积是( )【解析】选C.由斜二测画法原理知
△OAB中,OB=O′B′=1,
OA⊥OB,
∴△OAB的面积4. 如图矩形O′A′B′C′是水平
放置的一个平面图形的直观图,
其中O′A′=6,O′C′=2,则原
图形是( )
(A)正方形 (B)矩形
(C)菱形 (D)梯形【解析】选C.设B′C′与x′轴相交于点D′,还原的原图形如图所示,则
C′D′=O′C′=2,
CD=C′D′=2,
所以OC=OA,
又四边形OABC是平行四边形,
所以四边形OABC是菱形. 【方法技巧】巧断原图的形状和性质
在立体几何学习中,一定要逐步培养这样的能力“直观图
+概念 原图的形状和性质”.例如平行四边形、矩
形、菱形、正方形的水平放置的直观图都只保留下对边平
行且相等,所以只从直观图来看,无法全面准确地获取原
实物图形的性质,此时就需要结合有关概念进行推导,从
而准确判断原图的形状和性质.二、填空题(每题4分,共8分)
5.等腰直角三角形OAB的两条直
角边OA=AB=4,则它的直观图的
面积是___________.
【解析】在直观图中A′B′=2, 所以B′到x′轴的距离是
所以直观图的面积是
答案: 6一个四边形的斜二测直观图是一个底角为45°,腰和上底的长均为1的等腰梯形,那么原四边形的面积是__________.【解析】如图1所示,梯形O′A′B′C′中,O′C′=B′C′=1,∠A′O′C′=45°,
所以
根据斜二测画法的规则,原四边形OABC是直角梯形,且
OC=2O′C′=2,BC=B′C′=1.
所以原四边形的面积为
答案:三、解答题(每题8分,共16分)
7.如图所示,直角梯形ABCD中AB∥CD∥x轴,AD⊥AB,试画出此直角梯形水平放置的直观图.【解析】(1)过A作AE⊥x轴,垂足为E(如图(1)).另选平面
画直观图,先画x′轴和y′轴,使∠x′O′y′=45°.
(2)如图(2)在x′轴上截取O′E′=OE,过E′作E′A′∥y′
轴,截取 过A′作A′B′∥x′轴,截取A′B′= AB;过A′作A′D′∥y′轴,截取 过D′作D′C′∥x′轴,截取D′C′=DC.(3)连线成图(擦去辅助线)(如图(3))8.如图为水平放置的斜二测画法画出
的△ABO的直观图,试根据图中所给的
数据计算原三角形中BO、AB的长度.
【解析】由直观图可知:原三角形中BD⊥OA,OD=2,AD=1,BD=4.所以
【误区警示】解答本题时容易出现线段BD计算错误的情况,出错原因是忽视了斜二测画法画直观图时,与y轴平行的线段长度变为原来的一半.【挑战能力】
(10分)2010年海南省多灾并发、重
灾连发,尤其是国庆期间罕见的持
续强降雨,引发了特大的洪涝灾害
及山体滑坡等次生灾害,给人民群众生命财产造成了巨大损失.为帮助受灾群众早日重建家园,国家民政部迅速调拨支援海南省的4 000顶帐篷,于2010年10月14日晚到达海南省.救灾帐篷主体结构是四棱柱与三棱柱的组合体(如图),请用斜二测画法画出它的直观图.【解析】(1)画底面.(根据平面图形的直观图的画法)
(2)画z′轴(z′轴与x′轴的交角为90°),并画高(即PA与原长相等),连线成图.(3)擦去辅助线,被遮线画虚线.
1.建立直角坐标系时,要让原平面图形的顶点尽可能多地落在坐标轴或与坐标轴平行的线段上.
2.原图中不与x轴或y轴平行的线段,可以先作坐标轴的平行线为辅助线画出其端点,然后再连线.画水平放置的平面图形的直观图 水平放置的平面图形的直观图与原图形相比,平行关系是不变的,角的大小,线线垂直关系等都有可能变化.【例1】画出图中水平放置的直角梯形的直观图.
【审题指导】解答本题关键是建立适当的坐标系,根据斜二测画法的规则画出直角梯形的四个顶点.【规范解答】画法:
(1)在已知图形(直角梯形)所在平面上建立平面直角坐标系xOy.另选平面画直观图,先画x′轴和y′轴,使∠x′O′y′=45°.(2)将已知图形中平行于x轴或平行于y轴的线段在直观图中
分别画成平行于x′轴或平行于y′轴的线段,且已知图形
中平行于x轴的线段在直观图中保持原长度不变;平行于y
轴的线段,在直观图中长度为原来的(3)连线成图(擦去辅助线).【变式训练】画出图中四边形OABC的直观图(图中数据已给出).【解析】以O为原点,OB所在直线为x轴建立直角坐标系xOy,如图甲,如图乙,作∠x′O′y′=45°,其中O′B′=4,O′D′=3,
O′C′=1,过点D′作∠B′D′A′=135°,
使A′D′=1,顺次连接O′A′,A′B′,B′C′,擦去辅助线,所得四边形O′A′B′C′即为四边形OABC的直观图.【误区警示】解答本题容易在确定点A在直观图中的位置时
出错,出错原因一是不能根据AD∥y轴,通过画A′D′确定
点A′,二是忽视了1.画棱柱、棱锥的直观图可分以下四步:
(1)画轴:通常以高所在直线为z轴建系.
(2)画底面:根据平面图形的直观图画法确定底面.
(3)确定顶点:利用与z轴平行或在z轴上的线段确定有关顶点.
(4)连线成图.画立体图形的直观图2.画棱台的直观图可分以下四步:
(1)画轴:通常以高所在直线为z轴建系.
(2)画下底面.
(3)画高,画上底面.
(4)连线成图.
要注意最后对图形的修正:一要擦去辅助线,二要把被遮线画虚线.【例2】已知三棱锥P-ABC中PA与底面ABC垂直,四个面都
是直角三角形,且∠PAC=∠PAB=∠PBC=∠ABC=90°,
PA=1,AC=2, 试画此三棱锥的直观图.
【审题指导】解题的关键在于寻找此三棱锥的高,并以高所在的直线为z轴建系,画出底面的直观图,确定顶点P,连线成图.【规范解答】(1)画底面.(根据平面图形的直观图的画法)(如图1)(2)画z′轴(z′轴与x′轴的夹角为90°),并画高(即PA与原长相等),连线成图.(如图2)(3)擦去辅助线,被遮线画虚线.(如图3)【互动探究】本例中条件“已知三棱锥P-ABC中PA与底面ABC垂直,PA=1,AC=2”不变,其它条件改为“且∠PAC= ∠PAB=∠BAC=90°,AB=2”,则如何画此几何体的直观图.
【解题提示】解题时只要注意PA、AB、AC两两垂直,就可以建立恰当的坐标系画出直观图.【解析】(1)画底面.(根据平面图形的直观图的画法) (如图1)(2)画z′轴(z′轴与x′轴的交角为90°),并画高(即PA与原长相等),连线成图.(如图2)(3)擦去辅助线,被遮线画虚线.(如图3) 在斜二测画法中,直观图与原图的关系
(1)平行性不变.原图中互相平行的直线在直观图中仍然互相平行.
(2)共点、共线性不变.原图中相交于一点的直线,在直观图中仍然交于一点.原图中在一条直线上的点,在直观图中仍然在同一条直线上.
(3)平行线段的长度比不变.平面图形的直观图与原图形之间的关系 直观图的形状与原图相比有很大的变化,因此要借助斜二测画法的原理和有关公理定理,推断出原图的形状和性质,而不能只凭观察.【例3】在水平放置的平面α内有一边长为1的正
方形A′B′C′D′,如图,其中对角线A′C′水
平放置.已知该正方形是某个四边形用斜二测画
法画出的直观图,试画出该四边形的原图并求面积.
【审题指导】根据斜二测画法进行逆向思维,画出原图,再根据图中线的关系求面积.【规范解答】四边形ABCD的原图形如图所示.
∵A′C′水平放置,A′B′C′D′为正方形,
∴在四边形ABCD中,DA⊥AC.
∵DA=2D′A′=2,【变式训练】如图是△ABC利用斜二测画法得到的水平放置的直观图△A′B′C′,其中A′B′∥y′轴,B′C′∥x′轴,若△A′B′C′的面积是3,求△ABC的面积.【解析】由题意知△ABC为直角三角形,且AB⊥BC.
由斜二测画法的原理知AB=2A′B′,BC=B′C′,
又【例】如图所示,A′B′C′D′是
一个水平放置的平面图形的斜二测
直观图,已知A′B′C′D′是一个
直角梯形,A′B′∥C′D′,A′D′⊥C′D′且B′C′与y′轴平行,又A′B′=6,D′C′=4,A′D′=2,试求原图形ABCD的面积.【审题指导】解答本题的关键是首先根据斜二测画法的原理,判断出BC⊥AB,并计算线段BC、DC、AB的长度,然后再求原图形ABCD的面积.【规范解答】如图,由斜二测画法的原理知梯形A′B′C′D′的原图形ABCD为梯形,且BC⊥AB.
∵AB=A′B′=6,DC=D′C′=4,【变式备选】如图所示,△A′B′C′是水平放置的平面图形的斜二测直观图,将其恢复成原图形.【解析】画法:(1)画直角坐标系xOy,如图(2)所示,在x轴上取OA=O′A′,即CA=C′A′;
(2)在图(1)中,过B′作B′D′∥y′轴,交x′轴于D′,在x轴上取OD=O′D′,过D作DB∥y轴,并使DB=2D′B′.
(3)连接AB、BC,擦去辅助线,则△ABC即为△A′B′C′原来的图形,如图所示.【典例】(12分)已知等边三角形ABC的边长为a,试求△ABC的边AB水平放置时的直观图△A′B′C′的面积.
【审题指导】根据题目条件画出等边三角形ABC的实际图形和直观图,重点是分析底边长和高的变化情况.【规范解答】如图所示,作出等边三角形ABC的实际图形和直观图. …………………………………………………4分由图可知,A′B′=AB=a,………………………………6分
……………………………………8分
在图(2)中,作C′D′⊥A′B′于D′,
则 ………………………………10分
…………………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】等腰梯形ABCD中,上底边CD=1,
下底边AB=3,按平行于上、下底边取x轴,求该等腰梯形的直观图A′B′C′D′的面积.
【解析】等腰梯形ABCD的高为1,而直观图A′B′C′D′仍
为梯形,其高为 故面积为1.下面的说法正确的是( )
(A)水平放置的正方形的直观图可能是梯形
(B)两条相交的直线的直观图可能是平行直线
(C)互相垂直的两条直线的直观图仍然互相垂直
(D)水平放置的平行四边形的直观图仍是平行四边形
【解析】选D.水平放置的平面图形的直观图与原图形相比,平行关系是不变的,角的大小、线线垂直关系等都有可能变化,故选D.2.如图是用斜二测画法画某个图形
ABCDE的水平放置的直观图,则对
原图ABCDE,说法错误的是( )
(A)原图形ABCDE中∠CBA是直角
(B)原图形ABCDE中ED∥AB
(C)原图形ABCDE中∠EAB是直角
(D)原图形ABCDE中ED的长度小于AB的长度
【解析】选A.直观图中∠C′B′A′是直角,还原为原图形后是锐角,故错误.3.给出下列说法:
①水平放置的角的直观图一定是角;
②相等的角在直观图中仍相等;
③长度相等的线段在直观图中仍相等;
④如果一个三角形不是等腰三角形,那么该三角形水平放置的直观图一定不是等腰三角形.
其中叙述正确的个数是___________.【解析】水平放置的正方形的直观图是邻边不等的平行四边形,知②③错误.④错误.如下图所示Rt△OAB中OB=2OA, ∠AOB=90°,不是等腰三角形,但是该三角形水平放置的直观图是△O′A′B′,其中O′A′=O′B′是等腰三角形.
答案:14.如图为水平放置的正方形ABCO,它在直角坐标系xOy中点B的坐标为(2,2),则在用斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为___________.【解析】
B′到x′轴的距离为
答案: 5.画如图放置的直角三角形的直观图.【解析】画法:(1)画x′轴和y′轴,使∠x′O′y′=45°.
(2)在原图中作BD⊥x轴,垂足为D.
(3)截取O′A′=OA,
O′D′=OD, 且B′D′∥y′轴.
(4)连线成图.(擦去辅助线)一、选择题(每题4分,共16分)
1.利用斜二测画法得到:①三角形的水平放置的直观图是三角形;②平行四边形的水平放置的直观图是平行四边形;③正方形的水平放置的直观图是正方形;④菱形的水平放置的直观图是菱形.以上结论正确的是( )
(A)①② (B)①
(C)③④ (D)①②③④【解析】选A.水平放置的平面图形的直观图与原图形相比,角的大小、线线垂直关系、线段的长度等都有可能变化,故③④错误.2如图,用斜二测画法
画一个水平放置的平面图形的直观图为一个正
方形,则原来图形的形状是( ) 【解题提示】先计算直观图中坐标轴上线段的长度,再根据斜二测画法的原则,从长度和平行关系两个方面判断,选出正确答案.
【解析】选A.根据斜二测画法知,在y轴上的线段长度为直观图中长度的2倍,可知A正确.3.如图,
Rt△O′A′B′是一平面图形的直观
图,直角边O′B′=1,则这个平面
图形的原图形的面积是( )【解析】选C.由斜二测画法原理知
△OAB中,OB=O′B′=1,
OA⊥OB,
∴△OAB的面积4. 如图矩形O′A′B′C′是水平
放置的一个平面图形的直观图,
其中O′A′=6,O′C′=2,则原
图形是( )
(A)正方形 (B)矩形
(C)菱形 (D)梯形【解析】选C.设B′C′与x′轴相交于点D′,还原的原图形如图所示,则
C′D′=O′C′=2,
CD=C′D′=2,
所以OC=OA,
又四边形OABC是平行四边形,
所以四边形OABC是菱形. 【方法技巧】巧断原图的形状和性质
在立体几何学习中,一定要逐步培养这样的能力“直观图
+概念 原图的形状和性质”.例如平行四边形、矩
形、菱形、正方形的水平放置的直观图都只保留下对边平
行且相等,所以只从直观图来看,无法全面准确地获取原
实物图形的性质,此时就需要结合有关概念进行推导,从
而准确判断原图的形状和性质.二、填空题(每题4分,共8分)
5.等腰直角三角形OAB的两条直
角边OA=AB=4,则它的直观图的
面积是___________.
【解析】在直观图中A′B′=2, 所以B′到x′轴的距离是
所以直观图的面积是
答案: 6一个四边形的斜二测直观图是一个底角为45°,腰和上底的长均为1的等腰梯形,那么原四边形的面积是__________.【解析】如图1所示,梯形O′A′B′C′中,O′C′=B′C′=1,∠A′O′C′=45°,
所以
根据斜二测画法的规则,原四边形OABC是直角梯形,且
OC=2O′C′=2,BC=B′C′=1.
所以原四边形的面积为
答案:三、解答题(每题8分,共16分)
7.如图所示,直角梯形ABCD中AB∥CD∥x轴,AD⊥AB,试画出此直角梯形水平放置的直观图.【解析】(1)过A作AE⊥x轴,垂足为E(如图(1)).另选平面
画直观图,先画x′轴和y′轴,使∠x′O′y′=45°.
(2)如图(2)在x′轴上截取O′E′=OE,过E′作E′A′∥y′
轴,截取 过A′作A′B′∥x′轴,截取A′B′= AB;过A′作A′D′∥y′轴,截取 过D′作D′C′∥x′轴,截取D′C′=DC.(3)连线成图(擦去辅助线)(如图(3))8.如图为水平放置的斜二测画法画出
的△ABO的直观图,试根据图中所给的
数据计算原三角形中BO、AB的长度.
【解析】由直观图可知:原三角形中BD⊥OA,OD=2,AD=1,BD=4.所以
【误区警示】解答本题时容易出现线段BD计算错误的情况,出错原因是忽视了斜二测画法画直观图时,与y轴平行的线段长度变为原来的一半.【挑战能力】
(10分)2010年海南省多灾并发、重
灾连发,尤其是国庆期间罕见的持
续强降雨,引发了特大的洪涝灾害
及山体滑坡等次生灾害,给人民群众生命财产造成了巨大损失.为帮助受灾群众早日重建家园,国家民政部迅速调拨支援海南省的4 000顶帐篷,于2010年10月14日晚到达海南省.救灾帐篷主体结构是四棱柱与三棱柱的组合体(如图),请用斜二测画法画出它的直观图.【解析】(1)画底面.(根据平面图形的直观图的画法)
(2)画z′轴(z′轴与x′轴的交角为90°),并画高(即PA与原长相等),连线成图.(3)擦去辅助线,被遮线画虚线.
