1.3 三视图 课件3
图片预览










文档简介
课件30张PPT。1.3 三视图1.直观感受空间几何体的三视图形象.
2.会画简单的空间几何体(柱、锥、台、球及其组合)的三视图,能够识别三视图所描述的模型.
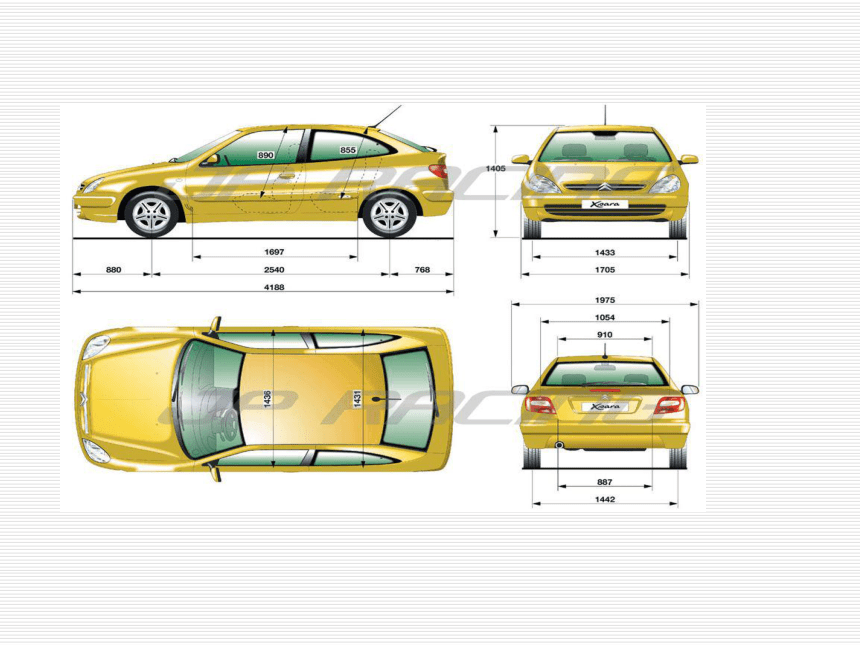
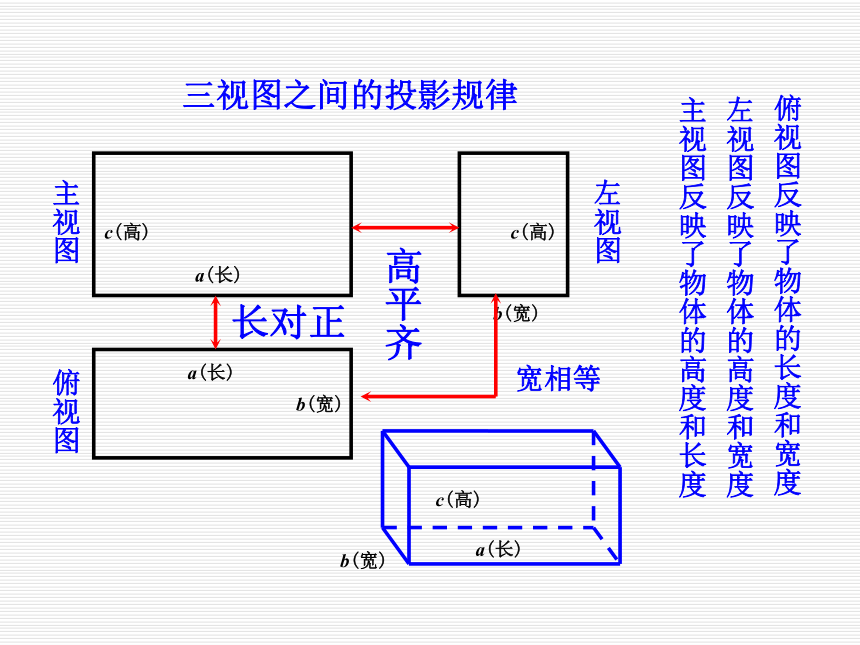
3.通过教学活动,逐步培养学生探索问题的精神.三视图欣赏 从不同的角度看同一物体,视觉的效果可能不同,要比较真实地反映出物体的特征,我们可从多角度观看物体.前面侧面上面1 从正前方研究物体的正投影图——2 从正左方研究物体的正投影图——3 从正上方研究物体的正投影图—— 几何体的主视图、左视图、俯视图合称为几何体的三视图.主视图(正视图)左视图(侧视图)俯视图在立体几何中,一般从三个方向研究物体思考1.三视图能反映物体真实的形状和长、宽、高吗?三个视图的长、宽、高之间有关系吗?主视图反映了物体的高度和长度 左视图反映了物体的高度和宽度 俯视图反映了物体的长度和宽度 主视图 左视图 俯视图 三视图之间的投影规律 思考2.如何具体画出一个空间几何体的三视图呢?有什么需要注意的细节问题吗?例1 画出正五棱锥的主视图.解 从主视方向看,该五棱锥有一条侧棱不可见,在主视图中,这条不可见侧棱用虚线画出.注意:在绘制三视图时,不可见边界轮廓线,用虚线画出.思考3.下面我们来看几组几何体,看一看它们有什么特征?(1)它们是将基本几何体拼接成的几何体.(2)它们是从基本几何体中切掉或挖掉部分构成的几何体. 一般地,由上述两种方式综合生成的几何体就是简单的组合体.简单组合体的三视图例2 画出右图所示物体的俯视图.解 该物体可以看作是由两个长方体组合而成的,俯视有不可见边界轮廓线(用虚线表示),如下图所示.例3 画出右图所示物体的主视图.解: 该物体可以看作是从长方体中先切掉一部分(三棱柱)得到的组合体.例4 螺栓是棱柱和圆柱拼接成的组合体,如图1-31所示,画出它的三视图.解 该物体是由一个正六棱柱和一个圆柱拼接而成的,主视图反映正六棱柱的三个侧面和圆柱侧面,左视图反映正六棱柱的两个侧面和圆柱侧面,俯视图反映该物体投影后是一个正六边形和一个圆(中心重合).主视图A俯视图左视图CDB例5 画出图1-33所示组合体的三视图.解 这是一个轴承架的模型(有轴承孔),它是由两个长方体和一个半圆柱体拼接而成,并挖去了一个与该半圆柱同心的圆柱(形成圆孔),在主视图和俯视图中为不可见轮廓线,用虚线画出,它的三视图为图1-34.绘制三视图时,要注意:1. 主、俯视图长对正;主、左视图高平齐;俯、左视图宽相等,前后对应.2. 在三视图中,需要画出所有的轮廓线,其中,视线所见的轮廓线画实线,看不见的轮廓线画虚线.3. 同一物体放置的位置不同,所画的三视图可能不同.4. 清楚简单组合体是由哪几个基本几何体组成的,并注意它们的组成方式,特别是它们的交线位置.思考4:我们由实物图可以画出它的三视图,实际生产中,工人要根据三视图加工零件,需要将三视图还原成实物,你能做到吗?四棱锥例6 一个几何体的三视图如下,你能说出它是什么立体图形吗? 例7 图1-35是4个三视图和4个实物图,请将三视图和实物图正确配对.解 (1)的实物图形是C;由(3)和(4)的俯视图可以看出:(3)(4)分别对应 B,A,于是(2)对应D.1、请同学们试试画出立白洗洁精塑料瓶的三视图.主视图左视图俯视图2、根据三视图判断几何体主视图左视图俯视图 3、想象下图所表示的实际物体.三通水管4、根据下列三视图,想象对应的几何体.三棱柱圆台四棱柱四棱柱与圆柱组成的简单组合体2、画几何体的三视图时,能看得见的轮廓线或棱用实线表示,不能看得见的轮廓线或棱用虚线表示.1、三视图之间的投影规律:
主视图与俯视图------长对正.
主视图与左视图------高平齐.
俯视图与左视图------宽相等. 3、培养空间想象能力,逆向思维能力.
2.会画简单的空间几何体(柱、锥、台、球及其组合)的三视图,能够识别三视图所描述的模型.
3.通过教学活动,逐步培养学生探索问题的精神.三视图欣赏 从不同的角度看同一物体,视觉的效果可能不同,要比较真实地反映出物体的特征,我们可从多角度观看物体.前面侧面上面1 从正前方研究物体的正投影图——2 从正左方研究物体的正投影图——3 从正上方研究物体的正投影图—— 几何体的主视图、左视图、俯视图合称为几何体的三视图.主视图(正视图)左视图(侧视图)俯视图在立体几何中,一般从三个方向研究物体思考1.三视图能反映物体真实的形状和长、宽、高吗?三个视图的长、宽、高之间有关系吗?主视图反映了物体的高度和长度 左视图反映了物体的高度和宽度 俯视图反映了物体的长度和宽度 主视图 左视图 俯视图 三视图之间的投影规律 思考2.如何具体画出一个空间几何体的三视图呢?有什么需要注意的细节问题吗?例1 画出正五棱锥的主视图.解 从主视方向看,该五棱锥有一条侧棱不可见,在主视图中,这条不可见侧棱用虚线画出.注意:在绘制三视图时,不可见边界轮廓线,用虚线画出.思考3.下面我们来看几组几何体,看一看它们有什么特征?(1)它们是将基本几何体拼接成的几何体.(2)它们是从基本几何体中切掉或挖掉部分构成的几何体. 一般地,由上述两种方式综合生成的几何体就是简单的组合体.简单组合体的三视图例2 画出右图所示物体的俯视图.解 该物体可以看作是由两个长方体组合而成的,俯视有不可见边界轮廓线(用虚线表示),如下图所示.例3 画出右图所示物体的主视图.解: 该物体可以看作是从长方体中先切掉一部分(三棱柱)得到的组合体.例4 螺栓是棱柱和圆柱拼接成的组合体,如图1-31所示,画出它的三视图.解 该物体是由一个正六棱柱和一个圆柱拼接而成的,主视图反映正六棱柱的三个侧面和圆柱侧面,左视图反映正六棱柱的两个侧面和圆柱侧面,俯视图反映该物体投影后是一个正六边形和一个圆(中心重合).主视图A俯视图左视图CDB例5 画出图1-33所示组合体的三视图.解 这是一个轴承架的模型(有轴承孔),它是由两个长方体和一个半圆柱体拼接而成,并挖去了一个与该半圆柱同心的圆柱(形成圆孔),在主视图和俯视图中为不可见轮廓线,用虚线画出,它的三视图为图1-34.绘制三视图时,要注意:1. 主、俯视图长对正;主、左视图高平齐;俯、左视图宽相等,前后对应.2. 在三视图中,需要画出所有的轮廓线,其中,视线所见的轮廓线画实线,看不见的轮廓线画虚线.3. 同一物体放置的位置不同,所画的三视图可能不同.4. 清楚简单组合体是由哪几个基本几何体组成的,并注意它们的组成方式,特别是它们的交线位置.思考4:我们由实物图可以画出它的三视图,实际生产中,工人要根据三视图加工零件,需要将三视图还原成实物,你能做到吗?四棱锥例6 一个几何体的三视图如下,你能说出它是什么立体图形吗? 例7 图1-35是4个三视图和4个实物图,请将三视图和实物图正确配对.解 (1)的实物图形是C;由(3)和(4)的俯视图可以看出:(3)(4)分别对应 B,A,于是(2)对应D.1、请同学们试试画出立白洗洁精塑料瓶的三视图.主视图左视图俯视图2、根据三视图判断几何体主视图左视图俯视图 3、想象下图所表示的实际物体.三通水管4、根据下列三视图,想象对应的几何体.三棱柱圆台四棱柱四棱柱与圆柱组成的简单组合体2、画几何体的三视图时,能看得见的轮廓线或棱用实线表示,不能看得见的轮廓线或棱用虚线表示.1、三视图之间的投影规律:
主视图与俯视图------长对正.
主视图与左视图------高平齐.
俯视图与左视图------宽相等. 3、培养空间想象能力,逆向思维能力.
