1.4 空间图形基本关系与公理 课件1
图片预览


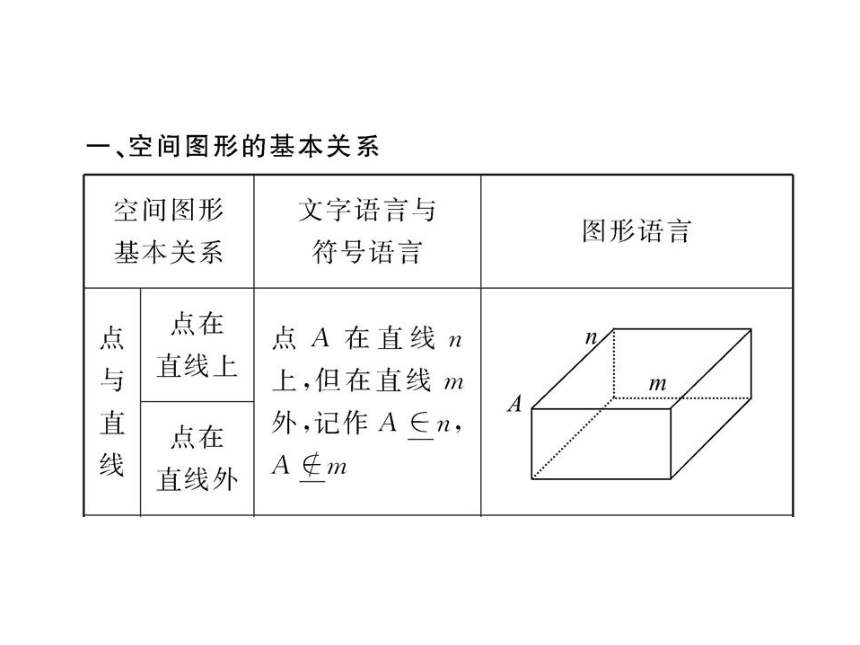
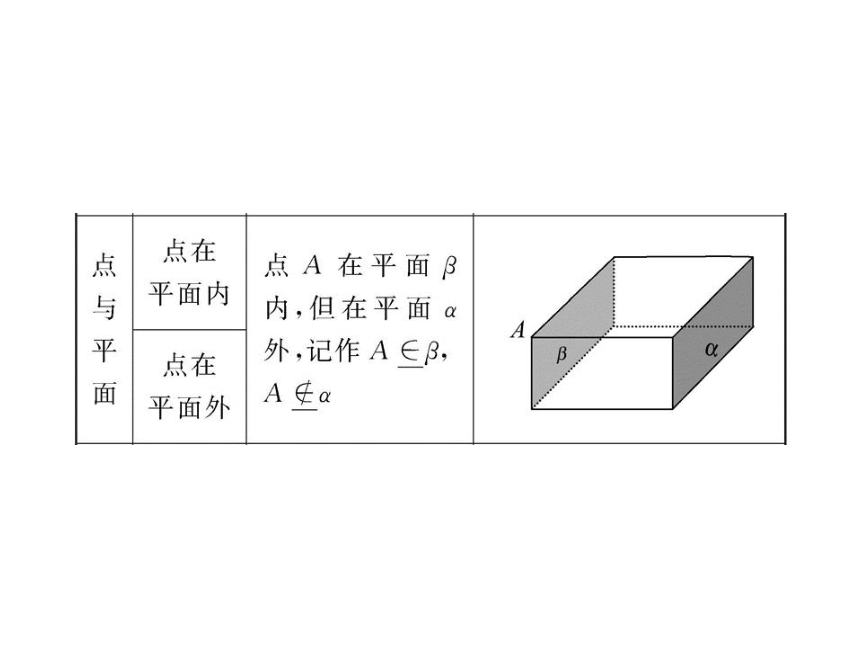

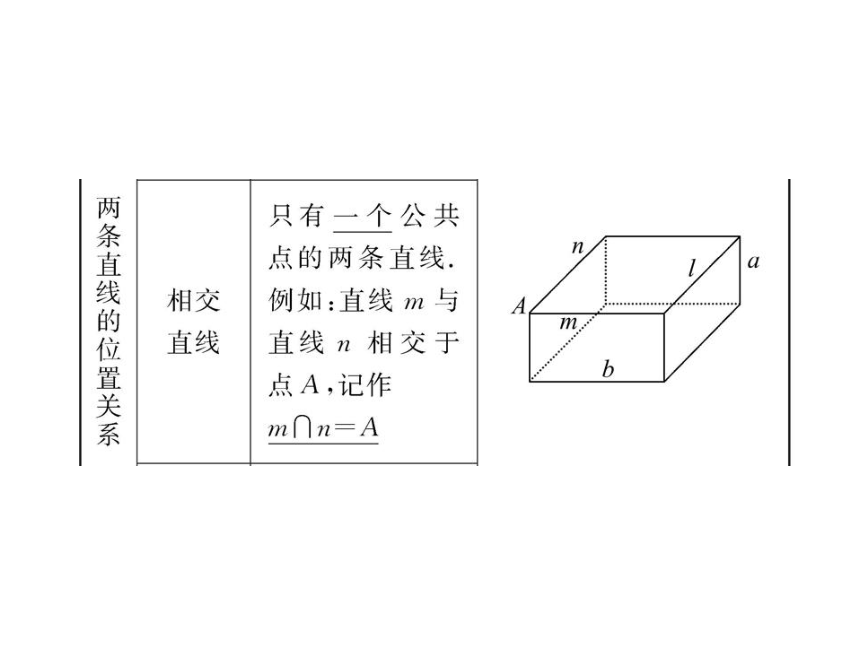


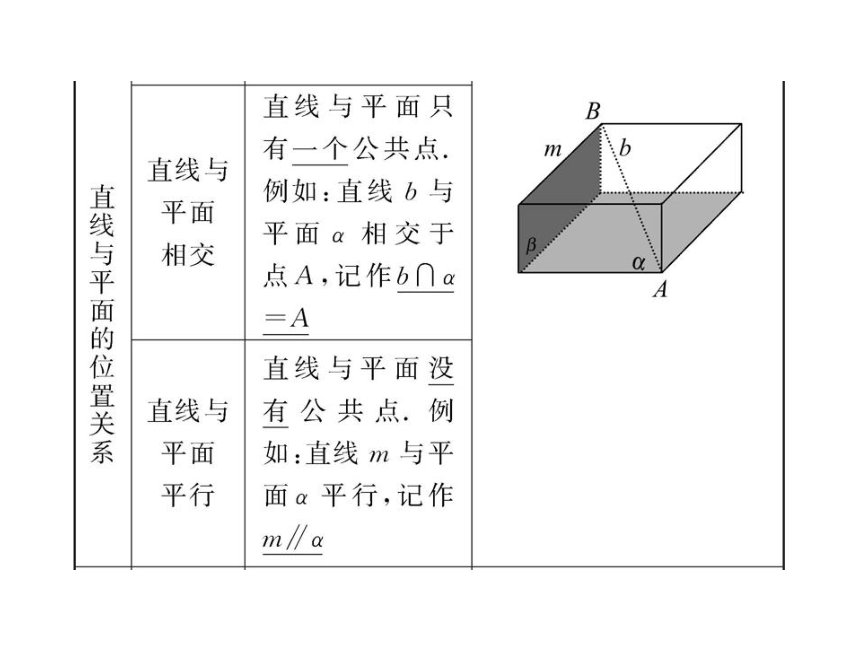

文档简介
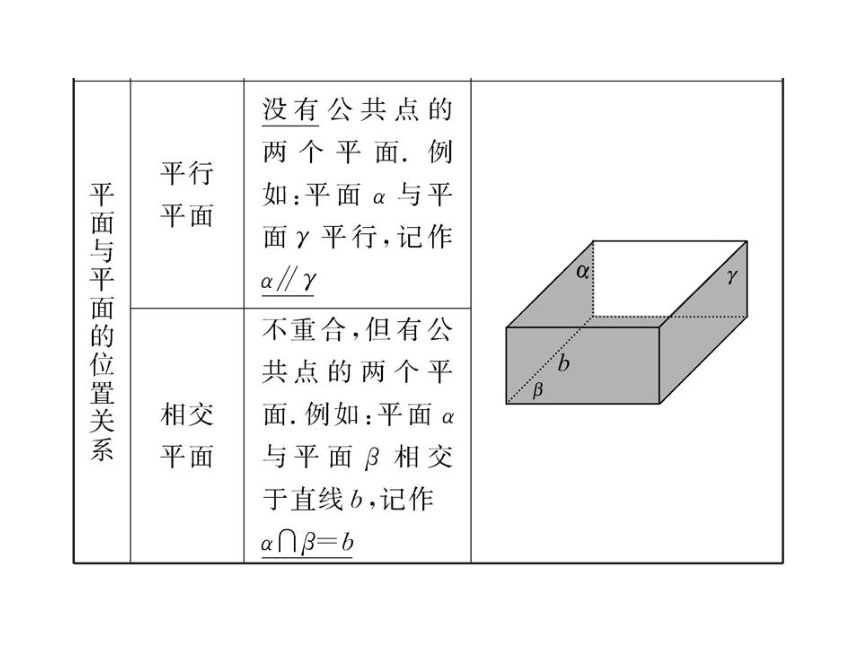
课件76张PPT。1.4.1 空间图形基本关系的认识 1.4.2 空间图形的公理(公理1、2、3) 文字语言、图形语言、符号语言的特点及相互关系
(1)符号语言简洁,层次感强,应用方便.
(2)文字语言比较自然、生动,它能将问题所研究的对象的含义更加明白地叙述出来,因此教科书中的概念、定理、公理等多以文字语言叙述.文字语言、图形语言、符号语
言的相互转化(3)图形语言易引起清晰的视觉形象,它能直观地表达概念、公理、定理的本质及相互关系,在抽象的数学思维面前起着具体化和加深理解的作用.【例1】依据下列数学符号语言画出图形:
(1)α∩β=l, m α ,n β , m∥l, n∥l;
(2)α∩β=l,直线PO α,直线PO∩直线l=O,直线
PA∩β=A,直线PB∩β=B;
(3)α∩β=a,△ABC的三个顶点满足条件A∈a,B∈α,
B a,C∈β,C a.
【审题指导】先从总体分析可知:三个小题中都有两个平面相交,再从局部分析两个平面交线及平面内点、线的位置,按由总体到局部的顺序作图.【规范解答】
(1)(2)
(3)【变式训练】试用数学符号语言表示下列图形中点、线、面之间的位置关系.【解析】(1)α∩β=m,n∩α=A,n∩β=B,A m,B m.
(2)α∩β=l,a α,b β,a∩l=P,b∩l=P.1.证明共面问题的依据
(1)公理2是确定平面的依据.它提供了把空间问题转化为平面问题的条件.共面问题(2)公理2的三个推论
推论1:经过一条直线和直线外的一点,有且只有一个平面;
推论2:经过两条相交直线,有且只有一个平面;
推论3:经过两条平行直线,有且只有一个平面.2.解决线共面问题的基本方法:
在空间图形中确定平面,把立体几何问题转化为平面几何问题,是解决立体几何问题的常用方法.【例2】已知A、B、C、D、E五点,A、B、C、D共面,B、C、D、E共面,则A、B、C、D、E五点一定共面吗?
【审题指导】本题是一个开放性问题,由A、B、C、D共面,B、C、D、E共面可考虑分B、C、D三点不共线和B、C、D三点共线两类讨论.【规范解答】(1)如果B、C、D三点不共线,则它们确定一个平面α.因为A、B、C、D共面,所以点A在平面α内.因为B、C、D、E共面,所以点E在平面α内,所以点A、E都在平面α内,即A、B、C、D、E五点一定共面.
(2)如果B、C、D三点共线于l,若A∈l,E∈l,则A、B、C、D、E五点一定共面.若A,E有且只有一个在l上,则A、B、C、D、E五点一定共面.若A,E都不在l上,则A、B、C、D、E五点可能不共面.【变式训练】已知:a∥b∥c,l∩a=A,l∩b=B,l∩c=C.
求证:直线a、b、c和l共面.
【解题提示】由a∥b知a和b确定一个平面,由b∥c知b和c确定另一个平面,这两个平面内都有直线l和直线b,由公理2的推论知这两个平面重合.【证明】∵a∥b,∴直线a与b确定一个平面,设为α,
∵l∩a=A,l∩b=B,
∴A∈a,B∈b,则A∈α,B∈α.
而A∈l,B∈l,∴由公理1可知:l α.
∵b∥c,∴直线b与c确定一个平面,设为β,
同理可知l β.∴平面α和平面β都包含直线b与l,
且l∩b=B.
又∵经过两条相交直线,有且只有一个平面,
∴平面α与平面β重合,
∴直线a,b,c和l共面.1.证明点共线与线共点的问题的理论依据
(1)证明点共线与线共点的实质都是要证明点在直线上.
(2)公理3是证明点在直线上的主要方法,其基本理论是把直线看作两平面的交线,点看作是两平面的公共点.可用数学符号表示为若α∩β=l,A∈α,A∈β,则A∈l.点共线与线共点的问题2.证明若干点共线的思路
找出两个平面的交线,然后证明各个点都是这两个平面的公共点.
3.证明若干直线共点的思路
先证两条直线交于一点,再证明其他直线经过该点,把问题转化为证明点在直线上的问题.【例3】如图,空间四边形ABCD中,
E、H分别是AB、AD的中点,F、G分
别是BC、CD上的点,且
求证:三条直线EF、GH、AC交于一
点.
【审题指导】要证三条直线EF、GH、AC交于一点,可先证直线EF与GH交于一点P,然后再证该交点P在直线AC上.【规范解答】∵E、H分别是AB、AD的中点,
∴EH∥BD,
∴EH∥GF且EH≠GF,
∴四边形EFGH为梯形,
∴两腰EF、GH交于一点P.∵EF 平面ABC,
∴P∈平面ABC,同理P∈平面ADC,
∴P在平面ADC和平面ABC的交线AC上,
∴三条直线EF、GH、AC交于一点.【变式训练】如图,已知在四边
形ABCD中,AB∥CD,AB、BC、CD、
DA所在直线分别与平面α交于E、
G、F、H,求证:E、G、F、H四点
共线.
【解题提示】证明本题可设法证明点E、F、G、H既在
平面α内又在直线AB和直线CD确定的平面内.【证明】∵AB∥CD,
∴AB与CD确定一个平面β.
∵点E、F、G、H分别在直线AB、CD、BC、AD上,
∴点E、F、G、H都在β内.
又∵点E、F、G、H都在α内,
∴点E、F、G、H在α与β的交线上.
又∵两个有公共点的不重合的平面有且只有一条交线,
故E、G、F、H四点共线.1.作两个平面的交线的基本思路
由公理3可知作两个平面的交线,只要确定这两个平面的两个公共点就可以解决了.
2.作某几何体的截面的基本思路
(1)利用公理2确定截面位置.
(2)利用公理3画截面与几何体表面的交线.截面及平面与平面交线的画法【例】如图所示,G是正方体ABCD-A1B1C1D1的棱DD1延长线上一点,E、F是棱AB、BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线.
(1)过点G及AC; (2)过三点E、F、D1.【审题指导】画截面的本质是确定截面与正方体表面的交线,也就是要确定截面与正方体表面的两个公共点.
【规范解答】(1)画法:连接GA交A1D1于点M,连接GC交C1D1于点N;连接MN、AC,则MA、CN、MN、AC为所求平面与正方体表面的交线.如图①所示.(2)画法:连接EF交DC的延长线于点P,交DA的延长线于点Q;连接D1P交CC1于点M,连接D1Q交AA1于点N;连接MF、NE,则D1M、MF、FE、EN、ND1为所求平面与正方体表面的交线.如图②所示.【变式备选】在正方体ABCD-A1B1C1D1中,E、F分别为CC1和AA1的中点,请你画出平面BED1F与平面ABCD的交线.【解析】画法:延长D1F,使D1F与DA的延长线交于点G,连接BG,BG即为平面ABCD与平面BED1F的
交线.
证明:在平面ADD1A1中,
∵AF∥DD1且
∴D1F与DA延长后应交于一点,
设为G,即有D1F∩DA=G.∵D1F 平面BED1F,G∈D1F,
∴G∈平面BED1F.
又DA 平面ABCD,G∈DA,∴G∈平面ABCD.
∴点G是平面ABCD与平面BED1F的公共点,
即点G在两个平面的交线上,从而可知直线BG是平面ABCD与平面BED1F的交线.【典例】(12分)如图所示,正方
体ABCD-A1B1C1D1中,M、N分别是
A1B1和B1C1的中点.问:
(1)AM和CN是否是异面直线?
(2)D1B和CC1是否是异面直线?
请说明理由.
【审题指导】根据异面直线的定义判定两条直线异面,比较困难.通常选取一个平面作为衬托,进行判断.【规范解答】(1)不是异面直线.理由如下:连接A1C1、AC、MN,……………………………………………………1分
∵在△A1B1C1中,M、N分别是A1B1和B1C1的中点,
∴MN是△A1B1C1的中位线,
∴MN∥A1C1. ………………………………………………2分又∵A1A∥D1D,A1A=D1D,D1D∥C1C,D1D=C1C,
∴A1A∥C1C,A1A=C1C,∴四边形A1ACC1是平行四边形,
……………………………………………………………4分
∴A1C1∥AC,得到MN∥AC,
∴A、M、N、C在同一个平面内,故AM、CN不是异面直线.
……………………………………………………………6分(2)是异面直线.理由如下:……………………………7分
∵直线CC 平面BB1C1C,………………………………8分
直线D1B∩平面BB1C1C=B, ……………………………10分
且B 直线CC1,
∴D1B与CC1是异面直线. ……………………………… 12分【误区警示】在解答本题时易犯的错误具体分析如下:【即时训练】如图,空间四边形ABCD中,
求证:对角线AC与BD为异面直线.
【证明】∵直线BC和直线CD相交,
可以确定一个平面,记此平面为α,
则直线BD α,
又∵直线AC∩α=C且C 直线BD,
∴AC与BD为异面直线.1.用符号表示“点A在直线l上,l在平面α外”,正确的是
( )
(A)A∈l,l α (B)A∈l,l α
(C)A l,l α (D)A l,l α
【解析】选A.集合观点下表示点、线、面的位置关系.点与线、点与面是元素与集合的关系,直线与平面是集合与集合的关系,故A正确.2.下列图形中不一定是平面图形的是( )
(A)三角形 (B)四边相等的四边形
(C)梯形 (D)平行四边形
【解析】选B.由互相平行的两条直线确定一个平面知C、D是平面图形,由相交的两条直线确定一个平面知A是平面图形,四边相等的四边形可能是空间四边形,故B不一定是平面图形.3.如图在四面体中,若直线EF和GH相交,
则它们的交点一定( )
(A)在直线DB上
(B)在直线AB上
(C)在直线CB上
(D)在直线AC上 【解析】选D.设直线EF∩直线GH=P,
则P∈直线EF 平面ABC,
P∈直线GH 平面ACD.
又平面ABC∩平面ACD=直线AC,
所以由公理3知P∈直线AC.4.对于结论“若a α且a∩b=P,则P∈α”,用文字语言
可以叙述为__________.
【解析】若直线a在平面α内且直线a与直线b相交于一点P,则点P一定在平面α内.
答案:若直线a与直线b相交于一点P且直线a在平面α内,则点P一定在平面α内5.画出满足下列条件的图形:
(1)三个平面:一个水平,一个竖直,一个倾斜;
(2)α∩β=l,直线AB α,AB∥l,E∈直线AB,直线
EF∩β=F,F l.【解析】(1)
(2) 一、选择题(每题4分,共16分)
1.下列叙述中错误的是( )
(A)若P∈α∩β且α∩β=l,则P∈l
(B)三点A,B,C只能确定一个平面
(C)若直线a∩b=A,则直线a与b能够确定一个平面
(D)若A∈l,B∈l且A∈α,B∈α,则l α
【解析】选B.只有不共线的三个点才能确定一个平面,因此B错误.由公理1知D正确,由两条相交直线可以确定一个平面的推论知C正确,由公理3知A正确.2.以下叙述正确的有( )
(1)若直线a、b共面,直线a、c共面,则直线b、c共面
(2)依次首尾相接的四条线段必共面.
(3)空间四点A、B、C、D共面但不共线,则AB、BC、CD、DA四条直线中总有两条直线平行.
(4)空间四点A、B、C、D共面但不共线,则AB与CD必相交.
(A)0个 (B)1个 (C)2个 (D)3个【解析】选A.(1)错误.因为共面不具有传递性.
(2)错误.依次首尾相接的四条线段可形成空间四边形,不一定共面.
(3)错误.若空间四点A、B、C、D共面但不共线,则AB,BC,CD,DA有可能两两相交.
(4)错误.若空间四点A、B、C、D共面但不共线,则AB与CD可以平行.3.下列说法正确的是( )
(A)平面α和平面β只有一个公共点
(B)两两相交的三条直线必共面
(C)不共面的四点中,任何三点不共线
(D)有三个公共点的两平面必重合【解析】选C.两平面若有公共点,则有无数个,故A错误;两两相交的三条直线若交于一点(如同一顶点正方体的三条棱),可能不共面,故B错误;C正确,因为四点中若有三点共线,则与第四个点确定一个平面,这与四点不共面矛盾;D错误,因为有三个公共点的平面可能相交.4.已知α,β,γ是平面,a,b,c是直线,α∩β=a,β∩γ=b,γ∩α=c,若a∩b=P,则( )
(A)P∈c (B)P c
(C)c∩a=? (D)c∩β=?
【解题提示】根据题目条件推断P∈α,P∈γ,进而由公理3推出P在α与γ的交线上.
【解析】选A.∵a∩b=P,∴P∈a且P∈b.
又∵a α,b γ,∴P∈α且P∈γ.
又∵α∩γ=c,∴P∈c. 二、填空题(每题4分,共8分)
5.如图,在正方体ABCD-A1B1C1D1中,
下列叙述正确的是____________.
(1)直线AC1 平面CC1B1B;
(2)设正方形ABCD与A1B1C1D1的中心
分别为O、O1,则平面AA1C1C∩平面BB1D1D=OO1;(3)点A、O、C只能确定一个平面;
(4)由点A、C1、B1确定的平面是ADC1B1;
(5)由点A、C1、B1确定的平面和由点A、C1、D确定的平面是同一平面.【解析】(1)错误.若直线AC1 平面CC1B1B,则A∈平面CC1B1B,这与正方体中A 平面CC1B1B矛盾;
(2)正确.因为O、O1是这两个平面的两个公共点;
(3)错误.因为点A、O、C在一条直线上;(4)正确.因为点A、C1、B1不共线,所以确定一个平面α.又因为AB1C1D是平行四边形,过AD与B1C1两平行线确定一个平面β,又α,β都过不共线三点A,C1,B1,所以α与β重合,所以点D∈平面AC1B1,即A、C1、B1确定的平面是ADC1B1;
(5)正确.原因类似(4).
答案: (2)(4)(5)6.将正方体纸盒展开(内表面如图所示),关于直线BM、ED、CN、DN、BE的叙述正确的是__________.
(1)BM与ED平行;
(2)CN与BM是异面直线;
(3)CN与BE是异面直线;
(4)DN与BM是异面直线.【解析】把平面图形还原为正方体
如图所示,正确的是(2)(4),观察
图形,根据两直线平行或异面的定
义可知,BM与ED是异面直线,CN与
BE平行,故(1)(3)错误.
答案:(2)(4) 【误区警示】解答本题容易出现以下错误:(1)还原为正方体时,各点在正方体中的位置出错.(2)对异面直线的判定方法不熟,而导致错误.三、解答题(每题8分,共16分)
7.如图,在
△ABC中,若AB、BC在平面α内,判
断AC是否在平面α内.
【解析】AC在平面α内,
∵AB在平面α内,∴A在平面α内,又∵BC在平面α内,
∴C在平面α内.∴点A、C都在平面α内,
∴直线AC在平面α内.8.已知,α∩β=m,b α,
C β,b∩m=A,c∥m,
求证: b,c是异面直线.【证明】假设b与c共面,则b∥c或b与c相交.
①若b∥c,由c∥m得m,b平行,这与m∩b=A矛盾.
②若b与c相交,不妨设c∩b=B,∵c β,b α,
故B∈β,B∈α,故B必在α、β的交线m上,即m与c相交
于点B,这与m∥c矛盾,故b与c不相交.
综合①②知,b与c是异面直线. 【方法技巧】巧证两条直线异面
(1)用定义证明:此时需要反证法,假设两条直线不异面,
根据空间两条直线的位置关系,这两条直线一定共面,即
这两条直线可能相交也可能平行,然后推导出矛盾,说明
相交和平行都不成立.
(2)用重要结论证明:用该法证明时,必须阐述清楚此结论
满足的条件:a α,A α,B∈α,B a,然后推导出
直线a与AB是异面直线.【挑战能力】
(10分)如图,定线段AB所在的直线与
定平面α相交,交点为O,P为定直线
外一点,P α,直线AP、BP与平面
α分别相交于A′,B′,试问,如果P
点任意移动,直线A′B′是否恒过一
定点,请说明理由.【解析】随着P点移动,直线A′B′恒过定点O,O为直线AB与平面α的交点.理由如下:
直线AB和直线外一点P可确定平面β,因为AP∩α=A′,BP∩α=B′,所以α∩β=A′B′,而AB∩α=O,所以O一定在交线A′B′上,即直线A′B′恒过定点O.
(1)符号语言简洁,层次感强,应用方便.
(2)文字语言比较自然、生动,它能将问题所研究的对象的含义更加明白地叙述出来,因此教科书中的概念、定理、公理等多以文字语言叙述.文字语言、图形语言、符号语
言的相互转化(3)图形语言易引起清晰的视觉形象,它能直观地表达概念、公理、定理的本质及相互关系,在抽象的数学思维面前起着具体化和加深理解的作用.【例1】依据下列数学符号语言画出图形:
(1)α∩β=l, m α ,n β , m∥l, n∥l;
(2)α∩β=l,直线PO α,直线PO∩直线l=O,直线
PA∩β=A,直线PB∩β=B;
(3)α∩β=a,△ABC的三个顶点满足条件A∈a,B∈α,
B a,C∈β,C a.
【审题指导】先从总体分析可知:三个小题中都有两个平面相交,再从局部分析两个平面交线及平面内点、线的位置,按由总体到局部的顺序作图.【规范解答】
(1)(2)
(3)【变式训练】试用数学符号语言表示下列图形中点、线、面之间的位置关系.【解析】(1)α∩β=m,n∩α=A,n∩β=B,A m,B m.
(2)α∩β=l,a α,b β,a∩l=P,b∩l=P.1.证明共面问题的依据
(1)公理2是确定平面的依据.它提供了把空间问题转化为平面问题的条件.共面问题(2)公理2的三个推论
推论1:经过一条直线和直线外的一点,有且只有一个平面;
推论2:经过两条相交直线,有且只有一个平面;
推论3:经过两条平行直线,有且只有一个平面.2.解决线共面问题的基本方法:
在空间图形中确定平面,把立体几何问题转化为平面几何问题,是解决立体几何问题的常用方法.【例2】已知A、B、C、D、E五点,A、B、C、D共面,B、C、D、E共面,则A、B、C、D、E五点一定共面吗?
【审题指导】本题是一个开放性问题,由A、B、C、D共面,B、C、D、E共面可考虑分B、C、D三点不共线和B、C、D三点共线两类讨论.【规范解答】(1)如果B、C、D三点不共线,则它们确定一个平面α.因为A、B、C、D共面,所以点A在平面α内.因为B、C、D、E共面,所以点E在平面α内,所以点A、E都在平面α内,即A、B、C、D、E五点一定共面.
(2)如果B、C、D三点共线于l,若A∈l,E∈l,则A、B、C、D、E五点一定共面.若A,E有且只有一个在l上,则A、B、C、D、E五点一定共面.若A,E都不在l上,则A、B、C、D、E五点可能不共面.【变式训练】已知:a∥b∥c,l∩a=A,l∩b=B,l∩c=C.
求证:直线a、b、c和l共面.
【解题提示】由a∥b知a和b确定一个平面,由b∥c知b和c确定另一个平面,这两个平面内都有直线l和直线b,由公理2的推论知这两个平面重合.【证明】∵a∥b,∴直线a与b确定一个平面,设为α,
∵l∩a=A,l∩b=B,
∴A∈a,B∈b,则A∈α,B∈α.
而A∈l,B∈l,∴由公理1可知:l α.
∵b∥c,∴直线b与c确定一个平面,设为β,
同理可知l β.∴平面α和平面β都包含直线b与l,
且l∩b=B.
又∵经过两条相交直线,有且只有一个平面,
∴平面α与平面β重合,
∴直线a,b,c和l共面.1.证明点共线与线共点的问题的理论依据
(1)证明点共线与线共点的实质都是要证明点在直线上.
(2)公理3是证明点在直线上的主要方法,其基本理论是把直线看作两平面的交线,点看作是两平面的公共点.可用数学符号表示为若α∩β=l,A∈α,A∈β,则A∈l.点共线与线共点的问题2.证明若干点共线的思路
找出两个平面的交线,然后证明各个点都是这两个平面的公共点.
3.证明若干直线共点的思路
先证两条直线交于一点,再证明其他直线经过该点,把问题转化为证明点在直线上的问题.【例3】如图,空间四边形ABCD中,
E、H分别是AB、AD的中点,F、G分
别是BC、CD上的点,且
求证:三条直线EF、GH、AC交于一
点.
【审题指导】要证三条直线EF、GH、AC交于一点,可先证直线EF与GH交于一点P,然后再证该交点P在直线AC上.【规范解答】∵E、H分别是AB、AD的中点,
∴EH∥BD,
∴EH∥GF且EH≠GF,
∴四边形EFGH为梯形,
∴两腰EF、GH交于一点P.∵EF 平面ABC,
∴P∈平面ABC,同理P∈平面ADC,
∴P在平面ADC和平面ABC的交线AC上,
∴三条直线EF、GH、AC交于一点.【变式训练】如图,已知在四边
形ABCD中,AB∥CD,AB、BC、CD、
DA所在直线分别与平面α交于E、
G、F、H,求证:E、G、F、H四点
共线.
【解题提示】证明本题可设法证明点E、F、G、H既在
平面α内又在直线AB和直线CD确定的平面内.【证明】∵AB∥CD,
∴AB与CD确定一个平面β.
∵点E、F、G、H分别在直线AB、CD、BC、AD上,
∴点E、F、G、H都在β内.
又∵点E、F、G、H都在α内,
∴点E、F、G、H在α与β的交线上.
又∵两个有公共点的不重合的平面有且只有一条交线,
故E、G、F、H四点共线.1.作两个平面的交线的基本思路
由公理3可知作两个平面的交线,只要确定这两个平面的两个公共点就可以解决了.
2.作某几何体的截面的基本思路
(1)利用公理2确定截面位置.
(2)利用公理3画截面与几何体表面的交线.截面及平面与平面交线的画法【例】如图所示,G是正方体ABCD-A1B1C1D1的棱DD1延长线上一点,E、F是棱AB、BC的中点.试分别画出过下列各点、直线的平面与正方体表面的交线.
(1)过点G及AC; (2)过三点E、F、D1.【审题指导】画截面的本质是确定截面与正方体表面的交线,也就是要确定截面与正方体表面的两个公共点.
【规范解答】(1)画法:连接GA交A1D1于点M,连接GC交C1D1于点N;连接MN、AC,则MA、CN、MN、AC为所求平面与正方体表面的交线.如图①所示.(2)画法:连接EF交DC的延长线于点P,交DA的延长线于点Q;连接D1P交CC1于点M,连接D1Q交AA1于点N;连接MF、NE,则D1M、MF、FE、EN、ND1为所求平面与正方体表面的交线.如图②所示.【变式备选】在正方体ABCD-A1B1C1D1中,E、F分别为CC1和AA1的中点,请你画出平面BED1F与平面ABCD的交线.【解析】画法:延长D1F,使D1F与DA的延长线交于点G,连接BG,BG即为平面ABCD与平面BED1F的
交线.
证明:在平面ADD1A1中,
∵AF∥DD1且
∴D1F与DA延长后应交于一点,
设为G,即有D1F∩DA=G.∵D1F 平面BED1F,G∈D1F,
∴G∈平面BED1F.
又DA 平面ABCD,G∈DA,∴G∈平面ABCD.
∴点G是平面ABCD与平面BED1F的公共点,
即点G在两个平面的交线上,从而可知直线BG是平面ABCD与平面BED1F的交线.【典例】(12分)如图所示,正方
体ABCD-A1B1C1D1中,M、N分别是
A1B1和B1C1的中点.问:
(1)AM和CN是否是异面直线?
(2)D1B和CC1是否是异面直线?
请说明理由.
【审题指导】根据异面直线的定义判定两条直线异面,比较困难.通常选取一个平面作为衬托,进行判断.【规范解答】(1)不是异面直线.理由如下:连接A1C1、AC、MN,……………………………………………………1分
∵在△A1B1C1中,M、N分别是A1B1和B1C1的中点,
∴MN是△A1B1C1的中位线,
∴MN∥A1C1. ………………………………………………2分又∵A1A∥D1D,A1A=D1D,D1D∥C1C,D1D=C1C,
∴A1A∥C1C,A1A=C1C,∴四边形A1ACC1是平行四边形,
……………………………………………………………4分
∴A1C1∥AC,得到MN∥AC,
∴A、M、N、C在同一个平面内,故AM、CN不是异面直线.
……………………………………………………………6分(2)是异面直线.理由如下:……………………………7分
∵直线CC 平面BB1C1C,………………………………8分
直线D1B∩平面BB1C1C=B, ……………………………10分
且B 直线CC1,
∴D1B与CC1是异面直线. ……………………………… 12分【误区警示】在解答本题时易犯的错误具体分析如下:【即时训练】如图,空间四边形ABCD中,
求证:对角线AC与BD为异面直线.
【证明】∵直线BC和直线CD相交,
可以确定一个平面,记此平面为α,
则直线BD α,
又∵直线AC∩α=C且C 直线BD,
∴AC与BD为异面直线.1.用符号表示“点A在直线l上,l在平面α外”,正确的是
( )
(A)A∈l,l α (B)A∈l,l α
(C)A l,l α (D)A l,l α
【解析】选A.集合观点下表示点、线、面的位置关系.点与线、点与面是元素与集合的关系,直线与平面是集合与集合的关系,故A正确.2.下列图形中不一定是平面图形的是( )
(A)三角形 (B)四边相等的四边形
(C)梯形 (D)平行四边形
【解析】选B.由互相平行的两条直线确定一个平面知C、D是平面图形,由相交的两条直线确定一个平面知A是平面图形,四边相等的四边形可能是空间四边形,故B不一定是平面图形.3.如图在四面体中,若直线EF和GH相交,
则它们的交点一定( )
(A)在直线DB上
(B)在直线AB上
(C)在直线CB上
(D)在直线AC上 【解析】选D.设直线EF∩直线GH=P,
则P∈直线EF 平面ABC,
P∈直线GH 平面ACD.
又平面ABC∩平面ACD=直线AC,
所以由公理3知P∈直线AC.4.对于结论“若a α且a∩b=P,则P∈α”,用文字语言
可以叙述为__________.
【解析】若直线a在平面α内且直线a与直线b相交于一点P,则点P一定在平面α内.
答案:若直线a与直线b相交于一点P且直线a在平面α内,则点P一定在平面α内5.画出满足下列条件的图形:
(1)三个平面:一个水平,一个竖直,一个倾斜;
(2)α∩β=l,直线AB α,AB∥l,E∈直线AB,直线
EF∩β=F,F l.【解析】(1)
(2) 一、选择题(每题4分,共16分)
1.下列叙述中错误的是( )
(A)若P∈α∩β且α∩β=l,则P∈l
(B)三点A,B,C只能确定一个平面
(C)若直线a∩b=A,则直线a与b能够确定一个平面
(D)若A∈l,B∈l且A∈α,B∈α,则l α
【解析】选B.只有不共线的三个点才能确定一个平面,因此B错误.由公理1知D正确,由两条相交直线可以确定一个平面的推论知C正确,由公理3知A正确.2.以下叙述正确的有( )
(1)若直线a、b共面,直线a、c共面,则直线b、c共面
(2)依次首尾相接的四条线段必共面.
(3)空间四点A、B、C、D共面但不共线,则AB、BC、CD、DA四条直线中总有两条直线平行.
(4)空间四点A、B、C、D共面但不共线,则AB与CD必相交.
(A)0个 (B)1个 (C)2个 (D)3个【解析】选A.(1)错误.因为共面不具有传递性.
(2)错误.依次首尾相接的四条线段可形成空间四边形,不一定共面.
(3)错误.若空间四点A、B、C、D共面但不共线,则AB,BC,CD,DA有可能两两相交.
(4)错误.若空间四点A、B、C、D共面但不共线,则AB与CD可以平行.3.下列说法正确的是( )
(A)平面α和平面β只有一个公共点
(B)两两相交的三条直线必共面
(C)不共面的四点中,任何三点不共线
(D)有三个公共点的两平面必重合【解析】选C.两平面若有公共点,则有无数个,故A错误;两两相交的三条直线若交于一点(如同一顶点正方体的三条棱),可能不共面,故B错误;C正确,因为四点中若有三点共线,则与第四个点确定一个平面,这与四点不共面矛盾;D错误,因为有三个公共点的平面可能相交.4.已知α,β,γ是平面,a,b,c是直线,α∩β=a,β∩γ=b,γ∩α=c,若a∩b=P,则( )
(A)P∈c (B)P c
(C)c∩a=? (D)c∩β=?
【解题提示】根据题目条件推断P∈α,P∈γ,进而由公理3推出P在α与γ的交线上.
【解析】选A.∵a∩b=P,∴P∈a且P∈b.
又∵a α,b γ,∴P∈α且P∈γ.
又∵α∩γ=c,∴P∈c. 二、填空题(每题4分,共8分)
5.如图,在正方体ABCD-A1B1C1D1中,
下列叙述正确的是____________.
(1)直线AC1 平面CC1B1B;
(2)设正方形ABCD与A1B1C1D1的中心
分别为O、O1,则平面AA1C1C∩平面BB1D1D=OO1;(3)点A、O、C只能确定一个平面;
(4)由点A、C1、B1确定的平面是ADC1B1;
(5)由点A、C1、B1确定的平面和由点A、C1、D确定的平面是同一平面.【解析】(1)错误.若直线AC1 平面CC1B1B,则A∈平面CC1B1B,这与正方体中A 平面CC1B1B矛盾;
(2)正确.因为O、O1是这两个平面的两个公共点;
(3)错误.因为点A、O、C在一条直线上;(4)正确.因为点A、C1、B1不共线,所以确定一个平面α.又因为AB1C1D是平行四边形,过AD与B1C1两平行线确定一个平面β,又α,β都过不共线三点A,C1,B1,所以α与β重合,所以点D∈平面AC1B1,即A、C1、B1确定的平面是ADC1B1;
(5)正确.原因类似(4).
答案: (2)(4)(5)6.将正方体纸盒展开(内表面如图所示),关于直线BM、ED、CN、DN、BE的叙述正确的是__________.
(1)BM与ED平行;
(2)CN与BM是异面直线;
(3)CN与BE是异面直线;
(4)DN与BM是异面直线.【解析】把平面图形还原为正方体
如图所示,正确的是(2)(4),观察
图形,根据两直线平行或异面的定
义可知,BM与ED是异面直线,CN与
BE平行,故(1)(3)错误.
答案:(2)(4) 【误区警示】解答本题容易出现以下错误:(1)还原为正方体时,各点在正方体中的位置出错.(2)对异面直线的判定方法不熟,而导致错误.三、解答题(每题8分,共16分)
7.如图,在
△ABC中,若AB、BC在平面α内,判
断AC是否在平面α内.
【解析】AC在平面α内,
∵AB在平面α内,∴A在平面α内,又∵BC在平面α内,
∴C在平面α内.∴点A、C都在平面α内,
∴直线AC在平面α内.8.已知,α∩β=m,b α,
C β,b∩m=A,c∥m,
求证: b,c是异面直线.【证明】假设b与c共面,则b∥c或b与c相交.
①若b∥c,由c∥m得m,b平行,这与m∩b=A矛盾.
②若b与c相交,不妨设c∩b=B,∵c β,b α,
故B∈β,B∈α,故B必在α、β的交线m上,即m与c相交
于点B,这与m∥c矛盾,故b与c不相交.
综合①②知,b与c是异面直线. 【方法技巧】巧证两条直线异面
(1)用定义证明:此时需要反证法,假设两条直线不异面,
根据空间两条直线的位置关系,这两条直线一定共面,即
这两条直线可能相交也可能平行,然后推导出矛盾,说明
相交和平行都不成立.
(2)用重要结论证明:用该法证明时,必须阐述清楚此结论
满足的条件:a α,A α,B∈α,B a,然后推导出
直线a与AB是异面直线.【挑战能力】
(10分)如图,定线段AB所在的直线与
定平面α相交,交点为O,P为定直线
外一点,P α,直线AP、BP与平面
α分别相交于A′,B′,试问,如果P
点任意移动,直线A′B′是否恒过一
定点,请说明理由.【解析】随着P点移动,直线A′B′恒过定点O,O为直线AB与平面α的交点.理由如下:
直线AB和直线外一点P可确定平面β,因为AP∩α=A′,BP∩α=B′,所以α∩β=A′B′,而AB∩α=O,所以O一定在交线A′B′上,即直线A′B′恒过定点O.
