1.4.2 空间图形的公理 课件1
图片预览


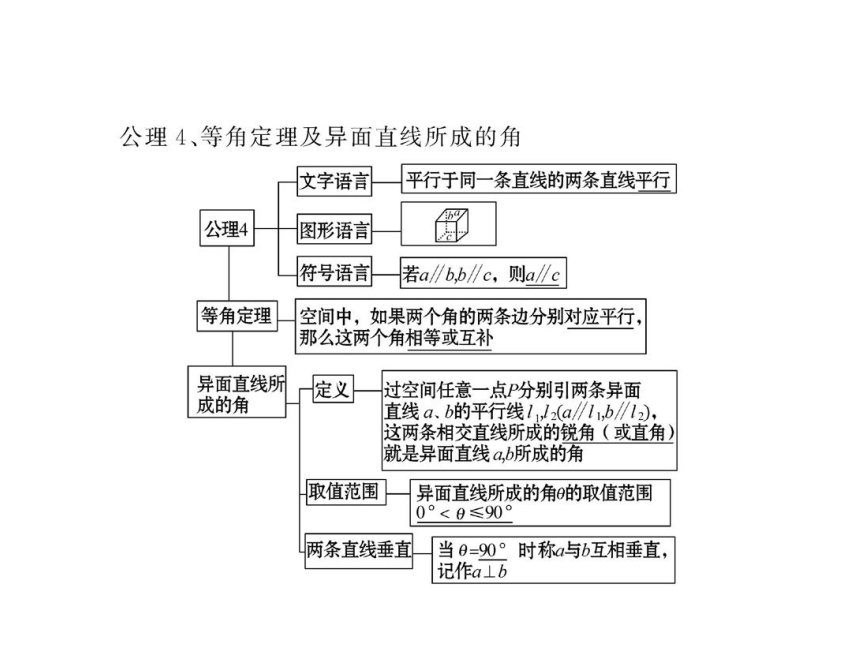









文档简介
课件74张PPT。1.4.2 空间图形的公理(公理4、定理) 对公理4的理解
(1)本质:表明了空间中线线平行的传递性.
(2)作用:公理4给出了空间两条直线平行的一种证明方法.它是论证平行问题的主要依据之一,也是研究空间两直线的位置关系、直线与平面位置关系的基础.公理4的应用(3)应用:“等角定理”的证明是公理4的直接应用.
(4)关键:寻找第三条直线分别与前两条直线平行是应用公理4证明线线平行的关键.也就是说,要证空间中的两直线平行,就要找一条与之平行的直线,利用传递性证明.
平面几何中的结论推广到空间之后,未必成立,其正确性是需要证明的,这一点在今后的学习中要特别注意.【例1】空间四边形ABCD中,E、F、G、
H分别为AB、BC、CD、AD上的点且
请回答并证明当空间
四边形ABCD的四条边及点G、H
(1)满足什么条件时,四边形EFGH为平行四边形?
(2)满足什么条件时,四边形EFGH为菱形?【审题指导】由 可想到利用平行线分线段成
比例定理证明EF∥AC;为使四边形EFGH为平行四边形,根
据公理4需证明GH AC;为使四边形EFGH为菱形,在(1)成
立的情况下,还需证明EH=EF,进一步可得AC、BD的关系.【规范解答】(1)当 时,四边形EFGH为平行四边形.
理由:
若
则HG∥AC且 ∴EF HG,
∴四边形EFGH为平行四边形.∥(2)当 且 时,
四边形EFGH为菱形.
理由:由(1)知,若
则四边形EFGH为平行四边形.
且
若 则
∴平行四边形EFGH为菱形.【互动探究】在本例中若条件不变,请回答下列问题并证明
(1)满足什么条件时,四边形EFGH为矩形;
(2)满足什么条件时,四边形EFGH为正方形.
【解题提示】解答本题一方面要应用公理4证明平行关系,另一方面要利用异面直线所成角的定义证明垂直关系.【解析】(1)当 且AC⊥BD时,四边形EFGH为矩形.
理由:由例题知 时,四边形EFGH为平行四边
形,
且EF∥HG∥AC,EH∥GF∥BD.
∴当AC⊥BD时,EF⊥EH,
∠HEF为90°.
∴四边形EFGH为矩形.(2)当 且AC⊥BD时,四边形EFGH为正方形.
理由:由例题(2)及上面所得(1)可知.
由 可知四边形EFGH为平行四边形.
由 及AC⊥BD得四边形EFGH为正方形.【例】如图,正方体ABCD-A1B1C1D1中,
AE=A1E1,AF=A1F1,P∈E1F1,(1)过P作
一条直线与棱CD平行,说明作法;
(2)求证:EF E1F1.
【审题指导】在空间中作已知直线的平行线,通常要考虑
用公理4;要证EF E1F1,只需证明四边形EFF1E1是平行四边形即可.【规范解答】(1)如图,
在平面A1B1C1D1内过P作
直线l∥C1D1,∵CD∥C1D1,
∴l∥CD,故l为所求作直线. (2)连接EE1,FF1.
∵AE A1E1,∴四边形AEE1A1为平行四边形,
∴AA1 E1E,同理AA1 F1F,
∴EE1 F1F,即四边形EFF1E1为平行四边形,
∴EF E1F1.【变式备选】如图所示,E、F分别是
长方体ABCD-A1B1C1D1的棱A1A、C1C的
中点.
求证:四边形B1EDF是平行四边形.【证明】设Q是DD1的中点,连接EQ,QC1,
∵E是AA1的中点,
∴EQ A1D1,
又在矩形A1B1C1D1中,A1D1 B1C1,
∴EQ B1C1,
∴四边形EQC1B1为平行四边形,
∴B1E C1Q.又∵Q、F分别是DD1、C1C两边的中点,
∴QD C1F.
∴四边形DQC1F为平行四边形,
∴C1Q DF.
又∵B1E C1Q,
∴B1E DF,
∴四边形B1EDF是平行四边形.【误区警示】证明此类问题时,同学们容易出现证明过程太简单,推理依据不充足,“想当然”地认为结论成立的情况,这种思维定势是学好立体几何的障碍之一. 对“等角定理”的理解
(1)本质:“等角定理”是平面几何中等角定理的类比推广.
(2)作用:①解决空间中角的平移的问题.②揭示空间中两条边对应平行的两个角的大小关系.“等角定理”的应用 (3)两个推论:
推论1 如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相同.
推论2 如果一个角的两边和另一个角的两边分别平行,并且有一组对边方向相同,另一组对边方向相反,那么这两个角互补.【例2】如图所示,在正方体ABCD
-A1B1C1D1 中,E、F、E1、F1分别
为所在边的中点.
求证:(1)EF E1F1;
(2)∠EA1F=∠E1CF1.
【审题指导】空间中证明线线平行,线段与线段长度相等,可以利用平行关系和线段长度关系的传递性,选择“中间线段”证明.空间中证明角与角相等,可以利用“等角定理”分别证明角的两条边分别平行,再结合图形得证.【规范解答】(1)连接BD、B1D1,
∵E、F分别为AD、AB的中点,
∴在△ABD中有EF∥BD,
且
∵E1 、F1分别为B1C1、C1D1的中点,∴在△C1D1B1中有E1F1∥B1D1且
而在正方体ABCD-A1B1C1D1 中,BB1 DD1,
∴四边形BB1D1D为平行四边形.
∴BD∥B1D1且BD=B1D1.
∴EF E1F1.(2)取A1B1的中点M,连接BM,F1M,则
又BF∥A1M,∴BF A1M,
∴四边形A1FBM为平行四边形.∴A1F∥BM.
而F1,M分别为C1D1,A1B1的中点,
则F1M C1B1,而C1B1 CB,
∴F1M∥BC且F1M=BC,
∴四边形F1MBC是平行四边形,
∴BM∥CF1,又BM∥A1F,∴A1F∥CF1.同理取A1D1的中点N,连接DN,E1N,则A1N DE,
∴四边形A1NDE是平行四边形,∴A1E∥DN.
易得E1N∥CD且E1N=CD,
∴四边形E1NDC是平行四边形.
∴DN∥CE1,∴A1E∥CE1,
∴∠EA1F与∠E1CF1的两边分别对应平行,
结合图形可知∠EA1F=∠E1CF1.【变式训练】如图,正方体ABCD
-A1B1C1D1中,E、F、G分别是棱CC1、
BB1、DD1的中点,
求证:∠BGC=∠FD1E.
【证明】∵E、F、G分别是棱CC1、
BB1、DD1的中点,∴CE GD1,BF GD1.
∴四边形CED1G与四边形BFD1G均是平行四边形.
∴GC∥D1E,GB∥D1F.
∴结合图形可知∠BGC=∠FD1E. 利用定义法求异面直线所成的角的一般步骤求异面直线所成的角 求异面直线所成的角的关键是“作角”,而“作角”的关键是恰当地利用平面几何中有关线线平行的结论作“辅助线”.【例3】如图,正方体ABCD-A1B1C1D1
中,E,F分别为A1B1,B1C1的中点,
求异面直线DB1与EF所成的角的大小.
【审题指导】求异面直线所成的角关
键在于“作角”,也就是利用平面几何知识作平行线,因此通常要把有关线段看作某三角形或平行四边形中的边.【规范解答】方法一:
如图,连接A1C1,B1D1,并设它
们相交于点O,取DD1的中点G,
连接OG.则OG∥B1D,EF∥A1C1
∴∠GOA1为异面直线DB1与EF所
成的角或其补角.
∵GA1=GC1,O为A1C1的中点,∴GO⊥A1C1,
∴异面直线DB1与EF所成的角为90°.方法二:如图,在原正方体的右侧补上一个全等的正方体,连接B1Q,则B1Q∥EF.于是,直线DB1与B1Q所成的较小的角就是异面直线DB1与EF所成的角,通过计算可知B1D2+B1Q2=DQ2,从而异面直线DB1与EF所成的角为90°.【变式训练】如图,棱长为2
的正方体ABCD-A1B1C1D1 中E、
F分别是A1B1、AB的中点,求
异面直线A1F与CE所成的角的正
切值.
【解题提示】解答本题可先在正方形AA1B1B中过点E作A1F的平行线,作出异面直线A1F与CE所成的角,然后在Rt△BCE中,计算所求角的正切值.【解析】连接BE,∵正方体ABCD-A1B1C1D1 中E、F分别是A1B1、AB的中点,
∴A1E∥BF,A1E=BF,
∴四边形A1EBF是平行四边形,
∴A1F∥BE,
∴∠BEC为异面直线A1F与CE所成的
角或其补角.
∵正方体ABCD-A1B1C1D1 的棱长为2,
BE⊥BC,∵BC=2,
∴∠BEC为异面直线A1F与CE所成的角,
∴异面直线A1F与CE所成的角的正切值为【典例】(12分)在正方体ABCD-
A1B1C1D1 中,点P在线段AD1上移动,
求异面直线CP与BA1所成的角θ的取
值范围.
【审题指导】由于线段CP的端点P在线段AD1上移动,所以应该过点C作辅助线平行直线A1B,作出异面直线CP与BA1所成的角θ,然后根据P点的变化,确定θ的取值范围.【规范解答】连接D1C,AC,
……………………2分
∵正方体ABCD-A1B1C1D1
中A1D1 AD BC,
∴四边形A1BCD1是平行
四边形,……………4分∴A1B∥CD1, ……………………………………………6分
∴异面直线CP与BA1所成的角θ即为∠D1CP,…………8分
由图可知CD1∥A1B,CA与A1B异面,当点P在线段AD1上移动时,0°<∠D1CP≤∠ACD1,
∴0°<θ≤60°. ………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】如图,空间四边形ABCD
中,两条对边AB=CD=3,E、F分别是
另外两条对边AD、BC上的点,且
求AB和CD所成
的角的大小.【解析】如图过E作EO∥AB,
交BD于点O.连接OF,
又
∴OF∥CD.
∴∠EOF(或其补角)是AB和CD所成的角.在△EOF中,
又
∴EF2=OE2+OF2,
∴∠EOF=90°.
即异面直线AB和CD所成的角为90°.1. a,b, c 为三条不重合的直线,如果 a ⊥c, b ⊥c ,则 a, b的位置关系必定是( )
(A)相交 (B)平行
(C)异面 (D)以上答案都不对
【解析】选D. 若a ⊥c, b ⊥c,则a与b相交,异面,平行都有可能. 2.在正方体ABCD-A1B1C1D1中,面对角线中与AD1成60°的有
( )
(A)4条 (B)6条
(C)8条 (D)10条【解析】选C.如图所示在正方体ABCD-
A1B1C1D1中,△AD1B1是等边三角形,故
B1D1,AB1与AD1所成的角是60°,同理
△ACD1也是等边三角形,AC,CD1与
AD1也成60°角,则在面对角线中,与
AC,CD1,B1D1,AB1分别平行的对角线与AD1也成60°角.3.如图,平面α与平面β相交于EF,
C∈EF,C′∈EF,AC α,
A′C′ α,BC β,B′C′ β
且AC∥A′C′, BC∥B′C′,
∠C=120°,∠C′=__________.
【解析】结合图形,AC∥A′C′,BC∥B′C′,根据等角定理,有∠C′=∠C=120°.
答案:120°4.在四棱锥P-ABCD中,PA⊥AB,底面ABCD是平行四边形,则PA与CD所成的角是___________.【解析】∵四边形ABCD是平行四边形,
∴ AB∥CD,
∴∠PAB是PA与CD所成的角.
又∵PA⊥AB,∴∠PAB=90°.
答案:90°5.如图,已知长方体ABCD-
EFGH中,
AE=2,
(1)求BC和EG所成的角.
(2)求AE和BG所成的角是多少度?【解析】(1)∵GF∥BC,
∴∠EGF(或其补角)为BC和EG所成的角.
在Rt△EFG中,易知∠EGF = 45°,
∴BC和EG所成的角是45°.
(2)∵BF∥AE ,
∴∠FBG(或其补角)为AE和BG所成的角.
在Rt△BFG中,易知∠FBG = 60°,
∴AE和BG所成的角是60°.一、选择题(每题4分,共16分)
1.已知a、b是异面直线,直线c∥直线a,那么c与b( )
(A)一定是异面直线 (B)一定是相交直线
(C)不可能是平行直线 (D)不可能是相交直线
【解析】选C.若c∥b,由公理4,∵c∥a,
∴a∥b,与a、b是异面直线矛盾.
∴c与b不可能平行.2.教室内有一把直尺,无论怎样放置,地面上总有这样的直线与该直尺所在直线( )
(A)平行 (B)垂直
(C)相交但不垂直 (D)异面
【解析】选B.直尺所在直线与地面有三种位置关系(1)直线与地面相交,A错,(2)直线与地面平行,C错,(3)直线在地面内,D错,这三种情况下地面上总有直线与直尺所在直线垂直.3.如图,
长方体ABCD-A′B′C′D′中截
去一部分,其中EH∥A′D′,
剩下的几何体是( )
(A)直五棱柱 (B)四棱台
(C)正五棱柱 (D)五棱锥 【解题提示】解答本题要紧扣棱柱、棱锥、棱台的定义判断,同时注意几何体观察角度的变化.
【解析】选A.把五边形ABFEA′和DCGHD′视为底面,由长方体的结构特征知剩余的几何体是直五棱柱.4.过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与棱AB,AD,AA1所在直线所成的角都相等,这样的直线l可以作( )
(A)1条 (B)2条
(C)3条 (D)4条【解析】选D.如图所示,AC1,AE,AF,AG都与棱AB,AD,AA1所成的角相等.二、填空题(每题4分,共8分)
5. 四面体PABC中,PA⊥BC,E、F分别为PC、AB上任一点,若EF与PA、BC所成的角分别为α、β,则α+β=_________.【解析】本题可利用特例法.如图,
若E、F分别为PC、AB中点时,
取AC中点M,连接EM、FM,
∴EM∥PA,FM∥BC.
∵PA⊥BC,∴∠FEM=α,
∠EFM=β,EM⊥FM,
∴α+β=90°.
答案:90°6.在四面体SABC中,SA⊥BC且 SA=BC,E, F分别为SC、AB 的中点,那么异面直线EF与SA 所成的角等于__________.【解析】取AC的中点D,连接DE、DF,
∵E, F分别为SC、AB 的中点,
∴DE∥SA,DF∥BC,
∴∠DEF为异面直线EF与SA 所成的角.
∵SA⊥BC,∴∠EDF=90°.
又∵SA=BC且∴DE=DF,∴△DEF是等腰直角三角形,
∴∠DEF=45°,即异面直线EF与SA 所成的角为45°.
答案:45° 【方法技巧】求异面直线所成角的诀窍
(1)平移方法:①中位线平移法.②平行四边形性质平移法.③补形平移法.
(2)平移直线是寻找两条异面直线所成角的过程,线的平移是在某个平面中进行的,该面的特点:①该平面包含其中一条异面直线,②该平面与另一条异面直线平行.
(3)求角或求角的三角函数值的一般步骤:①构造三角形,②解三角形求角或求角的三角函数值.三、解答题(每题8分,共16分)
7.如图所示,不共面的三条直线a、
b、c交于点O,在点O的同侧分别取点
A和A1,B和B1,C和C1,使得
求证:△ABC∽△A1B1C1.【证明】
∴A1B1∥AB.
∴B1C1∥BC.
结合图形,由等角定理可得∠A1B1C1=∠ABC.
同理可证∠B1A1C1=∠BAC.
∴△ABC∽△A1B1C1 .8.直三棱柱ABC-A1B1C1中∠ACB=90°,
D1,F1分别是A1B1,A1C1的中点.若
BC=CA=CC1=2,求异面直线BD1与
AF1所成的角.
【解题提示】解答本题可考虑过
点F1(或A)作BD1的平行线,构造三角形得到异面直线所成的角,通过判断三角形形状求角.【解析】方法一:取BC中点G,连接F1G,AG,则D1F1∥B1C1且
又∵B1C1 BC,G为BC的中点,
∴D1F1 BG,
∴四边形D1F1GB是平行四边形,
∴BD1∥F1G,
∴∠AF1G(或其补角)为异面直线BD1与AF1所成的角.在Rt△ACG中,
同理在Rt△BB1D1,Rt△A1AF1可求
又BD1= GF1,故△AGF1是等边三角形,∴∠AF1G=60°,
∴异面直线BD1 与AF1所成的角是60°.方法二:延展平面BAA1B1,
使A1E=D1A1,
易得BD1∥AE,∠EAF1(或其补角 )
即为BD1与AF1所成的角.与方法一
类似可证△AEF1是等边三角形,
得∠EAF1=60°.
即异面直线BD1与AF1所成的角是60°.【挑战能力】
(10分)在长方体ABCD-A1B1C1D1的面A1C1上有一点P(如图所示,其中P点不在对角线B1D1上).
(1)过P点在空间中作一直线l,
使l∥直线BD,应该如何作图?
并说明理由;
(2)过P点在平面A1C1内作一直线m,使m与直线BD成α角,其中0°<α≤90°,这样的直线有几条,应该如何作图?【解析】(1)连接B1D1,在平面A1C1内过P作直线l,
使l∥B1D1,则l即为所求作的直线.
∵B1D1∥BD,l∥B1D1,
∴l∥直线BD.(2)在平面A1C1内作直线m,
使直线m与B1D1相交成α角,
∵BD∥B1D1,∴直线m与直线BD也成α角,
即直线m为所求作的直线.
由图知m与BD是异面直线,
且m与BD所成的角0°<α≤90°.
当α=90°时,这样的直线m有且只有一条,
当α≠90°时,这样的直线m有两条.
(1)本质:表明了空间中线线平行的传递性.
(2)作用:公理4给出了空间两条直线平行的一种证明方法.它是论证平行问题的主要依据之一,也是研究空间两直线的位置关系、直线与平面位置关系的基础.公理4的应用(3)应用:“等角定理”的证明是公理4的直接应用.
(4)关键:寻找第三条直线分别与前两条直线平行是应用公理4证明线线平行的关键.也就是说,要证空间中的两直线平行,就要找一条与之平行的直线,利用传递性证明.
平面几何中的结论推广到空间之后,未必成立,其正确性是需要证明的,这一点在今后的学习中要特别注意.【例1】空间四边形ABCD中,E、F、G、
H分别为AB、BC、CD、AD上的点且
请回答并证明当空间
四边形ABCD的四条边及点G、H
(1)满足什么条件时,四边形EFGH为平行四边形?
(2)满足什么条件时,四边形EFGH为菱形?【审题指导】由 可想到利用平行线分线段成
比例定理证明EF∥AC;为使四边形EFGH为平行四边形,根
据公理4需证明GH AC;为使四边形EFGH为菱形,在(1)成
立的情况下,还需证明EH=EF,进一步可得AC、BD的关系.【规范解答】(1)当 时,四边形EFGH为平行四边形.
理由:
若
则HG∥AC且 ∴EF HG,
∴四边形EFGH为平行四边形.∥(2)当 且 时,
四边形EFGH为菱形.
理由:由(1)知,若
则四边形EFGH为平行四边形.
且
若 则
∴平行四边形EFGH为菱形.【互动探究】在本例中若条件不变,请回答下列问题并证明
(1)满足什么条件时,四边形EFGH为矩形;
(2)满足什么条件时,四边形EFGH为正方形.
【解题提示】解答本题一方面要应用公理4证明平行关系,另一方面要利用异面直线所成角的定义证明垂直关系.【解析】(1)当 且AC⊥BD时,四边形EFGH为矩形.
理由:由例题知 时,四边形EFGH为平行四边
形,
且EF∥HG∥AC,EH∥GF∥BD.
∴当AC⊥BD时,EF⊥EH,
∠HEF为90°.
∴四边形EFGH为矩形.(2)当 且AC⊥BD时,四边形EFGH为正方形.
理由:由例题(2)及上面所得(1)可知.
由 可知四边形EFGH为平行四边形.
由 及AC⊥BD得四边形EFGH为正方形.【例】如图,正方体ABCD-A1B1C1D1中,
AE=A1E1,AF=A1F1,P∈E1F1,(1)过P作
一条直线与棱CD平行,说明作法;
(2)求证:EF E1F1.
【审题指导】在空间中作已知直线的平行线,通常要考虑
用公理4;要证EF E1F1,只需证明四边形EFF1E1是平行四边形即可.【规范解答】(1)如图,
在平面A1B1C1D1内过P作
直线l∥C1D1,∵CD∥C1D1,
∴l∥CD,故l为所求作直线. (2)连接EE1,FF1.
∵AE A1E1,∴四边形AEE1A1为平行四边形,
∴AA1 E1E,同理AA1 F1F,
∴EE1 F1F,即四边形EFF1E1为平行四边形,
∴EF E1F1.【变式备选】如图所示,E、F分别是
长方体ABCD-A1B1C1D1的棱A1A、C1C的
中点.
求证:四边形B1EDF是平行四边形.【证明】设Q是DD1的中点,连接EQ,QC1,
∵E是AA1的中点,
∴EQ A1D1,
又在矩形A1B1C1D1中,A1D1 B1C1,
∴EQ B1C1,
∴四边形EQC1B1为平行四边形,
∴B1E C1Q.又∵Q、F分别是DD1、C1C两边的中点,
∴QD C1F.
∴四边形DQC1F为平行四边形,
∴C1Q DF.
又∵B1E C1Q,
∴B1E DF,
∴四边形B1EDF是平行四边形.【误区警示】证明此类问题时,同学们容易出现证明过程太简单,推理依据不充足,“想当然”地认为结论成立的情况,这种思维定势是学好立体几何的障碍之一. 对“等角定理”的理解
(1)本质:“等角定理”是平面几何中等角定理的类比推广.
(2)作用:①解决空间中角的平移的问题.②揭示空间中两条边对应平行的两个角的大小关系.“等角定理”的应用 (3)两个推论:
推论1 如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相同.
推论2 如果一个角的两边和另一个角的两边分别平行,并且有一组对边方向相同,另一组对边方向相反,那么这两个角互补.【例2】如图所示,在正方体ABCD
-A1B1C1D1 中,E、F、E1、F1分别
为所在边的中点.
求证:(1)EF E1F1;
(2)∠EA1F=∠E1CF1.
【审题指导】空间中证明线线平行,线段与线段长度相等,可以利用平行关系和线段长度关系的传递性,选择“中间线段”证明.空间中证明角与角相等,可以利用“等角定理”分别证明角的两条边分别平行,再结合图形得证.【规范解答】(1)连接BD、B1D1,
∵E、F分别为AD、AB的中点,
∴在△ABD中有EF∥BD,
且
∵E1 、F1分别为B1C1、C1D1的中点,∴在△C1D1B1中有E1F1∥B1D1且
而在正方体ABCD-A1B1C1D1 中,BB1 DD1,
∴四边形BB1D1D为平行四边形.
∴BD∥B1D1且BD=B1D1.
∴EF E1F1.(2)取A1B1的中点M,连接BM,F1M,则
又BF∥A1M,∴BF A1M,
∴四边形A1FBM为平行四边形.∴A1F∥BM.
而F1,M分别为C1D1,A1B1的中点,
则F1M C1B1,而C1B1 CB,
∴F1M∥BC且F1M=BC,
∴四边形F1MBC是平行四边形,
∴BM∥CF1,又BM∥A1F,∴A1F∥CF1.同理取A1D1的中点N,连接DN,E1N,则A1N DE,
∴四边形A1NDE是平行四边形,∴A1E∥DN.
易得E1N∥CD且E1N=CD,
∴四边形E1NDC是平行四边形.
∴DN∥CE1,∴A1E∥CE1,
∴∠EA1F与∠E1CF1的两边分别对应平行,
结合图形可知∠EA1F=∠E1CF1.【变式训练】如图,正方体ABCD
-A1B1C1D1中,E、F、G分别是棱CC1、
BB1、DD1的中点,
求证:∠BGC=∠FD1E.
【证明】∵E、F、G分别是棱CC1、
BB1、DD1的中点,∴CE GD1,BF GD1.
∴四边形CED1G与四边形BFD1G均是平行四边形.
∴GC∥D1E,GB∥D1F.
∴结合图形可知∠BGC=∠FD1E. 利用定义法求异面直线所成的角的一般步骤求异面直线所成的角 求异面直线所成的角的关键是“作角”,而“作角”的关键是恰当地利用平面几何中有关线线平行的结论作“辅助线”.【例3】如图,正方体ABCD-A1B1C1D1
中,E,F分别为A1B1,B1C1的中点,
求异面直线DB1与EF所成的角的大小.
【审题指导】求异面直线所成的角关
键在于“作角”,也就是利用平面几何知识作平行线,因此通常要把有关线段看作某三角形或平行四边形中的边.【规范解答】方法一:
如图,连接A1C1,B1D1,并设它
们相交于点O,取DD1的中点G,
连接OG.则OG∥B1D,EF∥A1C1
∴∠GOA1为异面直线DB1与EF所
成的角或其补角.
∵GA1=GC1,O为A1C1的中点,∴GO⊥A1C1,
∴异面直线DB1与EF所成的角为90°.方法二:如图,在原正方体的右侧补上一个全等的正方体,连接B1Q,则B1Q∥EF.于是,直线DB1与B1Q所成的较小的角就是异面直线DB1与EF所成的角,通过计算可知B1D2+B1Q2=DQ2,从而异面直线DB1与EF所成的角为90°.【变式训练】如图,棱长为2
的正方体ABCD-A1B1C1D1 中E、
F分别是A1B1、AB的中点,求
异面直线A1F与CE所成的角的正
切值.
【解题提示】解答本题可先在正方形AA1B1B中过点E作A1F的平行线,作出异面直线A1F与CE所成的角,然后在Rt△BCE中,计算所求角的正切值.【解析】连接BE,∵正方体ABCD-A1B1C1D1 中E、F分别是A1B1、AB的中点,
∴A1E∥BF,A1E=BF,
∴四边形A1EBF是平行四边形,
∴A1F∥BE,
∴∠BEC为异面直线A1F与CE所成的
角或其补角.
∵正方体ABCD-A1B1C1D1 的棱长为2,
BE⊥BC,∵BC=2,
∴∠BEC为异面直线A1F与CE所成的角,
∴异面直线A1F与CE所成的角的正切值为【典例】(12分)在正方体ABCD-
A1B1C1D1 中,点P在线段AD1上移动,
求异面直线CP与BA1所成的角θ的取
值范围.
【审题指导】由于线段CP的端点P在线段AD1上移动,所以应该过点C作辅助线平行直线A1B,作出异面直线CP与BA1所成的角θ,然后根据P点的变化,确定θ的取值范围.【规范解答】连接D1C,AC,
……………………2分
∵正方体ABCD-A1B1C1D1
中A1D1 AD BC,
∴四边形A1BCD1是平行
四边形,……………4分∴A1B∥CD1, ……………………………………………6分
∴异面直线CP与BA1所成的角θ即为∠D1CP,…………8分
由图可知CD1∥A1B,CA与A1B异面,当点P在线段AD1上移动时,0°<∠D1CP≤∠ACD1,
∴0°<θ≤60°. ………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】如图,空间四边形ABCD
中,两条对边AB=CD=3,E、F分别是
另外两条对边AD、BC上的点,且
求AB和CD所成
的角的大小.【解析】如图过E作EO∥AB,
交BD于点O.连接OF,
又
∴OF∥CD.
∴∠EOF(或其补角)是AB和CD所成的角.在△EOF中,
又
∴EF2=OE2+OF2,
∴∠EOF=90°.
即异面直线AB和CD所成的角为90°.1. a,b, c 为三条不重合的直线,如果 a ⊥c, b ⊥c ,则 a, b的位置关系必定是( )
(A)相交 (B)平行
(C)异面 (D)以上答案都不对
【解析】选D. 若a ⊥c, b ⊥c,则a与b相交,异面,平行都有可能. 2.在正方体ABCD-A1B1C1D1中,面对角线中与AD1成60°的有
( )
(A)4条 (B)6条
(C)8条 (D)10条【解析】选C.如图所示在正方体ABCD-
A1B1C1D1中,△AD1B1是等边三角形,故
B1D1,AB1与AD1所成的角是60°,同理
△ACD1也是等边三角形,AC,CD1与
AD1也成60°角,则在面对角线中,与
AC,CD1,B1D1,AB1分别平行的对角线与AD1也成60°角.3.如图,平面α与平面β相交于EF,
C∈EF,C′∈EF,AC α,
A′C′ α,BC β,B′C′ β
且AC∥A′C′, BC∥B′C′,
∠C=120°,∠C′=__________.
【解析】结合图形,AC∥A′C′,BC∥B′C′,根据等角定理,有∠C′=∠C=120°.
答案:120°4.在四棱锥P-ABCD中,PA⊥AB,底面ABCD是平行四边形,则PA与CD所成的角是___________.【解析】∵四边形ABCD是平行四边形,
∴ AB∥CD,
∴∠PAB是PA与CD所成的角.
又∵PA⊥AB,∴∠PAB=90°.
答案:90°5.如图,已知长方体ABCD-
EFGH中,
AE=2,
(1)求BC和EG所成的角.
(2)求AE和BG所成的角是多少度?【解析】(1)∵GF∥BC,
∴∠EGF(或其补角)为BC和EG所成的角.
在Rt△EFG中,易知∠EGF = 45°,
∴BC和EG所成的角是45°.
(2)∵BF∥AE ,
∴∠FBG(或其补角)为AE和BG所成的角.
在Rt△BFG中,易知∠FBG = 60°,
∴AE和BG所成的角是60°.一、选择题(每题4分,共16分)
1.已知a、b是异面直线,直线c∥直线a,那么c与b( )
(A)一定是异面直线 (B)一定是相交直线
(C)不可能是平行直线 (D)不可能是相交直线
【解析】选C.若c∥b,由公理4,∵c∥a,
∴a∥b,与a、b是异面直线矛盾.
∴c与b不可能平行.2.教室内有一把直尺,无论怎样放置,地面上总有这样的直线与该直尺所在直线( )
(A)平行 (B)垂直
(C)相交但不垂直 (D)异面
【解析】选B.直尺所在直线与地面有三种位置关系(1)直线与地面相交,A错,(2)直线与地面平行,C错,(3)直线在地面内,D错,这三种情况下地面上总有直线与直尺所在直线垂直.3.如图,
长方体ABCD-A′B′C′D′中截
去一部分,其中EH∥A′D′,
剩下的几何体是( )
(A)直五棱柱 (B)四棱台
(C)正五棱柱 (D)五棱锥 【解题提示】解答本题要紧扣棱柱、棱锥、棱台的定义判断,同时注意几何体观察角度的变化.
【解析】选A.把五边形ABFEA′和DCGHD′视为底面,由长方体的结构特征知剩余的几何体是直五棱柱.4.过正方体ABCD-A1B1C1D1的顶点A作直线l,使l与棱AB,AD,AA1所在直线所成的角都相等,这样的直线l可以作( )
(A)1条 (B)2条
(C)3条 (D)4条【解析】选D.如图所示,AC1,AE,AF,AG都与棱AB,AD,AA1所成的角相等.二、填空题(每题4分,共8分)
5. 四面体PABC中,PA⊥BC,E、F分别为PC、AB上任一点,若EF与PA、BC所成的角分别为α、β,则α+β=_________.【解析】本题可利用特例法.如图,
若E、F分别为PC、AB中点时,
取AC中点M,连接EM、FM,
∴EM∥PA,FM∥BC.
∵PA⊥BC,∴∠FEM=α,
∠EFM=β,EM⊥FM,
∴α+β=90°.
答案:90°6.在四面体SABC中,SA⊥BC且 SA=BC,E, F分别为SC、AB 的中点,那么异面直线EF与SA 所成的角等于__________.【解析】取AC的中点D,连接DE、DF,
∵E, F分别为SC、AB 的中点,
∴DE∥SA,DF∥BC,
∴∠DEF为异面直线EF与SA 所成的角.
∵SA⊥BC,∴∠EDF=90°.
又∵SA=BC且∴DE=DF,∴△DEF是等腰直角三角形,
∴∠DEF=45°,即异面直线EF与SA 所成的角为45°.
答案:45° 【方法技巧】求异面直线所成角的诀窍
(1)平移方法:①中位线平移法.②平行四边形性质平移法.③补形平移法.
(2)平移直线是寻找两条异面直线所成角的过程,线的平移是在某个平面中进行的,该面的特点:①该平面包含其中一条异面直线,②该平面与另一条异面直线平行.
(3)求角或求角的三角函数值的一般步骤:①构造三角形,②解三角形求角或求角的三角函数值.三、解答题(每题8分,共16分)
7.如图所示,不共面的三条直线a、
b、c交于点O,在点O的同侧分别取点
A和A1,B和B1,C和C1,使得
求证:△ABC∽△A1B1C1.【证明】
∴A1B1∥AB.
∴B1C1∥BC.
结合图形,由等角定理可得∠A1B1C1=∠ABC.
同理可证∠B1A1C1=∠BAC.
∴△ABC∽△A1B1C1 .8.直三棱柱ABC-A1B1C1中∠ACB=90°,
D1,F1分别是A1B1,A1C1的中点.若
BC=CA=CC1=2,求异面直线BD1与
AF1所成的角.
【解题提示】解答本题可考虑过
点F1(或A)作BD1的平行线,构造三角形得到异面直线所成的角,通过判断三角形形状求角.【解析】方法一:取BC中点G,连接F1G,AG,则D1F1∥B1C1且
又∵B1C1 BC,G为BC的中点,
∴D1F1 BG,
∴四边形D1F1GB是平行四边形,
∴BD1∥F1G,
∴∠AF1G(或其补角)为异面直线BD1与AF1所成的角.在Rt△ACG中,
同理在Rt△BB1D1,Rt△A1AF1可求
又BD1= GF1,故△AGF1是等边三角形,∴∠AF1G=60°,
∴异面直线BD1 与AF1所成的角是60°.方法二:延展平面BAA1B1,
使A1E=D1A1,
易得BD1∥AE,∠EAF1(或其补角 )
即为BD1与AF1所成的角.与方法一
类似可证△AEF1是等边三角形,
得∠EAF1=60°.
即异面直线BD1与AF1所成的角是60°.【挑战能力】
(10分)在长方体ABCD-A1B1C1D1的面A1C1上有一点P(如图所示,其中P点不在对角线B1D1上).
(1)过P点在空间中作一直线l,
使l∥直线BD,应该如何作图?
并说明理由;
(2)过P点在平面A1C1内作一直线m,使m与直线BD成α角,其中0°<α≤90°,这样的直线有几条,应该如何作图?【解析】(1)连接B1D1,在平面A1C1内过P作直线l,
使l∥B1D1,则l即为所求作的直线.
∵B1D1∥BD,l∥B1D1,
∴l∥直线BD.(2)在平面A1C1内作直线m,
使直线m与B1D1相交成α角,
∵BD∥B1D1,∴直线m与直线BD也成α角,
即直线m为所求作的直线.
由图知m与BD是异面直线,
且m与BD所成的角0°<α≤90°.
当α=90°时,这样的直线m有且只有一条,
当α≠90°时,这样的直线m有两条.
