1.5.1 平行关系的判定 课件2
图片预览





文档简介
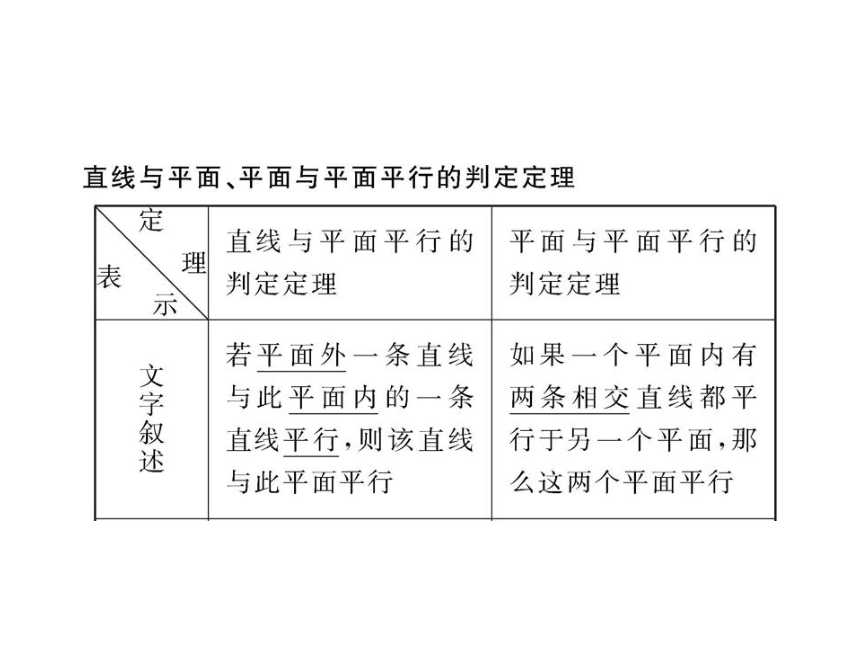
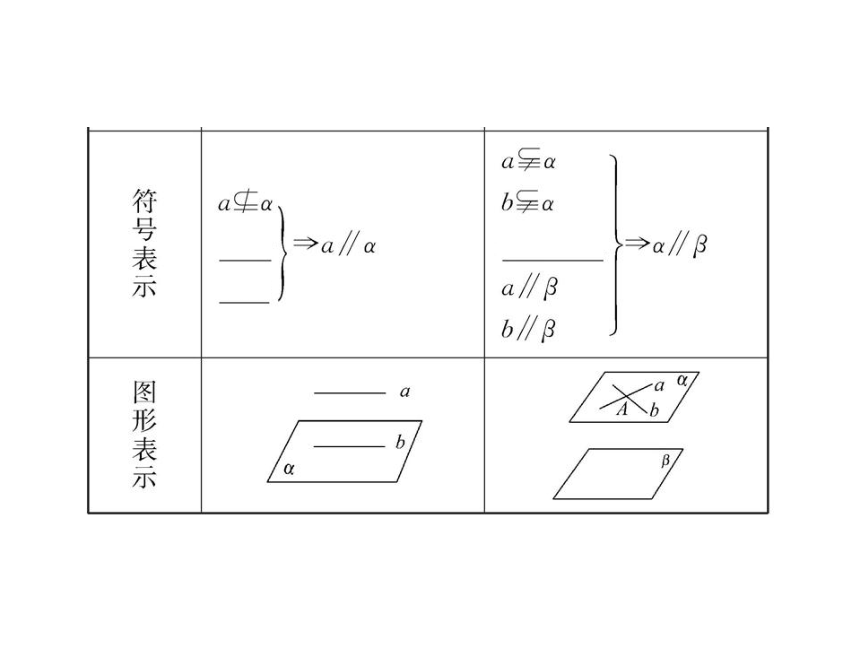
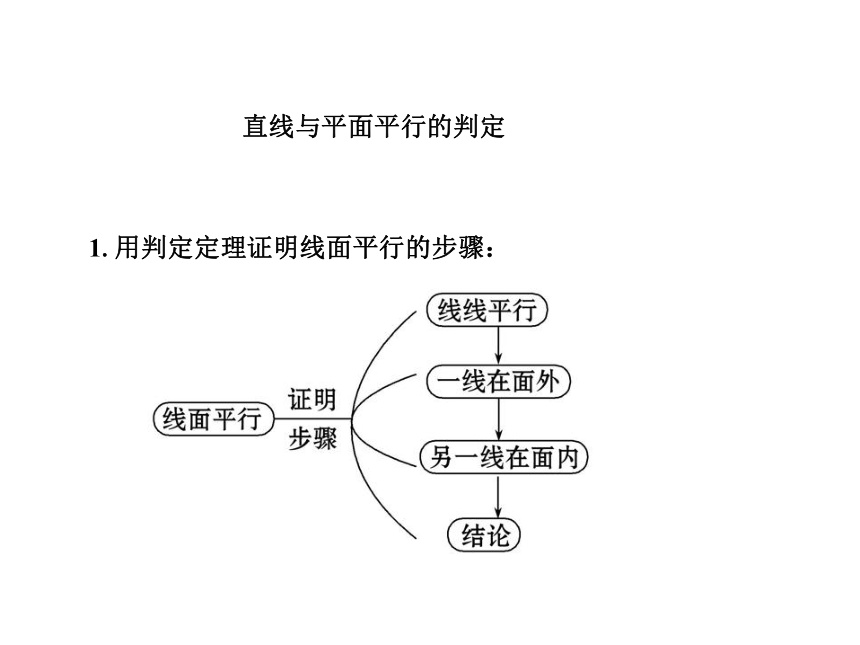
课件69张PPT。1.5.1 平行关系的判定 1.用判定定理证明线面平行的步骤:直线与平面平行的判定2.线面平行的判定定理在使用时三个条件缺一不可:
(1)直线a不在平面α内,即a α.
(2)直线b在平面α内,即b α.
(3)两条直线a、b平行,即a∥b.
要注意线面平行关系不具有传递性,即
如果a∥b,a∥α,那么b与α不一定平行.实际上,此时有
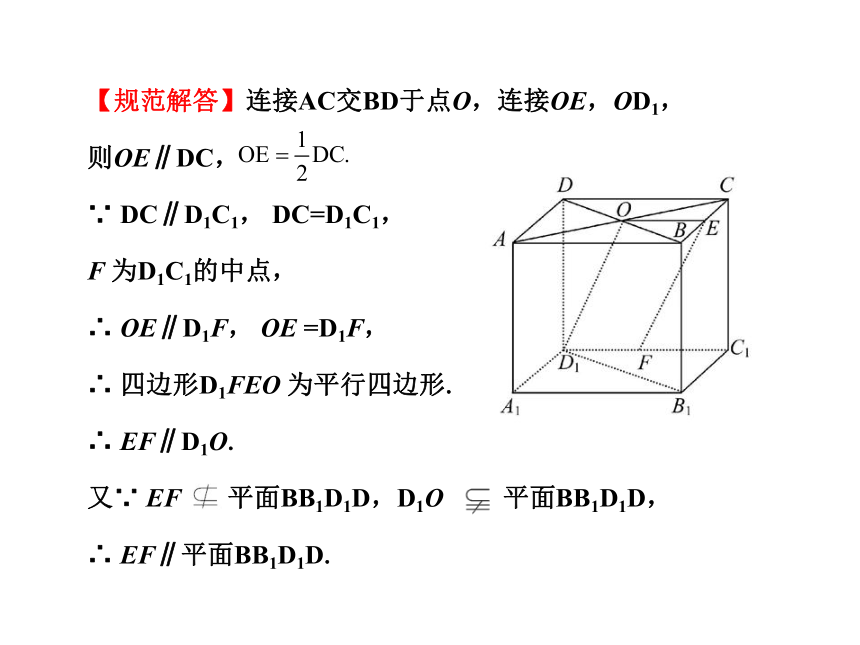
B α和b∥α两种情况.【例1】在正方体ABCD-A1B1C1D1中,
E、F 分别为棱BC、C1D1 的中点.
求证:EF∥平面BB1D1D.
【审题指导】在平面BB1D1D内找到一条直线与直线EF平行是证明本题的关键,根据图形中直线与平面的位置关系,可考虑用平行四边形的性质作辅助线证明.【规范解答】连接AC交BD于点O,连接OE,OD1,
则OE∥DC,
∵ DC∥D1C1, DC=D1C1,
F 为D1C1的中点,
∴ OE∥D1F, OE =D1F,
∴ 四边形D1FEO 为平行四边形.
∴ EF∥D1O.
又∵ EF 平面BB1D1D,D1O 平面BB1D1D,
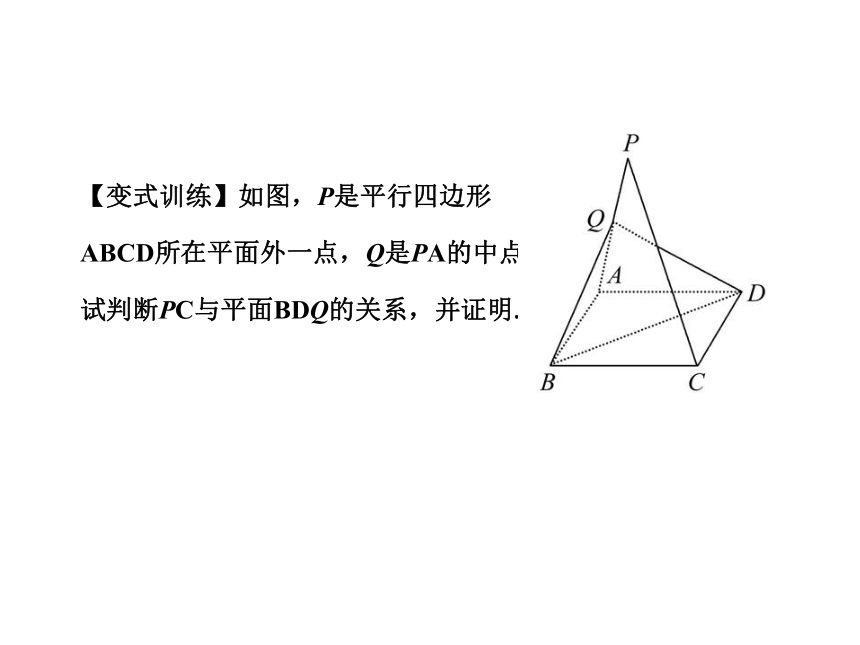
∴ EF∥平面BB1D1D.【变式训练】如图,P是平行四边形
ABCD所在平面外一点,Q是PA的中点,
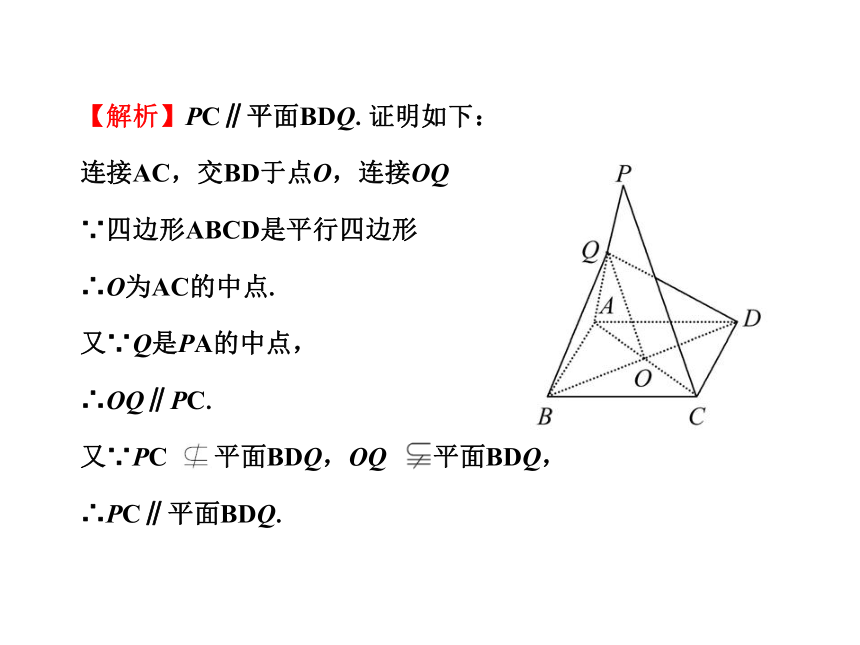
试判断PC与平面BDQ的关系,并证明.【解析】PC∥平面BDQ.证明如下:
连接AC,交BD于点O,连接OQ
∵四边形ABCD是平行四边形
∴O为AC的中点.
又∵Q是PA的中点,
∴OQ∥PC.
又∵PC 平面BDQ,OQ 平面BDQ,
∴PC∥平面BDQ. 【误区警示】解答本题的过程中易漏掉条件PC 平
面BDQ及OQ 平面BDQ,在利用线面平行的判定定理证明线
面平行时,定理中的三个条件缺一不可.【例】如图,四边形ABCD,ADEF都是
正方形,M∈BD,N∈AE,且BM=AN.
求证:MN∥平面CED.
【审题指导】要证MN∥平面CED,就要在平面CED内找一条直线与直线MN平行,可以用以下两个办法:(1)连接AM并延长与CD相交,在三角形中寻找线线平行;(2)分别过点M、N作AD的平行线,利用平行四边形的性质寻找线线平行.【规范解答】方法一:如图(1),连接
AM并延长交CD于点G,连接GE,
因为AB∥CD,所以
所以
即又因为BD=AE且AN=BM,
所以
所以MN∥GE,
又GE 平面CED,
MN 平面CED,
所以MN∥平面CED.方法二:如图(2),
过点M在平面ABCD中作MS∥AD交CD于点S,过点N在平面ADEF中作NT∥AD交DE于点T,连接ST.
因为MS∥AD,AD∥BC,
所以MS∥BC,
所以
因为BM=AN,BD=AE,所以BD-BM=AE-AN,即DM=EN.所以
又因为NT∥AD,
所以 所以
因为AD=BC,所以MS=NT.
又因为MS∥AD,NT∥AD,所以MS∥NT,
所以四边形MSTN为平行四边形,所以MN∥ST.
又因为MN 平面CED,ST 平面CED,
所以MN∥平面CED.【变式备选】
如图所示,三棱柱ABC—A1B1C1中,E是AC的中点,求证:AB1∥平面BEC1.【证明】连接B1C交BC1于O点,
则O为B1C的中点,连接EO,
平面AB1C∩平面BEC1=EO,
在△AB1C中,EO为△AB1C的
中位线,∴AB1∥EO,
又∵AB1 平面BEC1,
EO 平面BEC1,
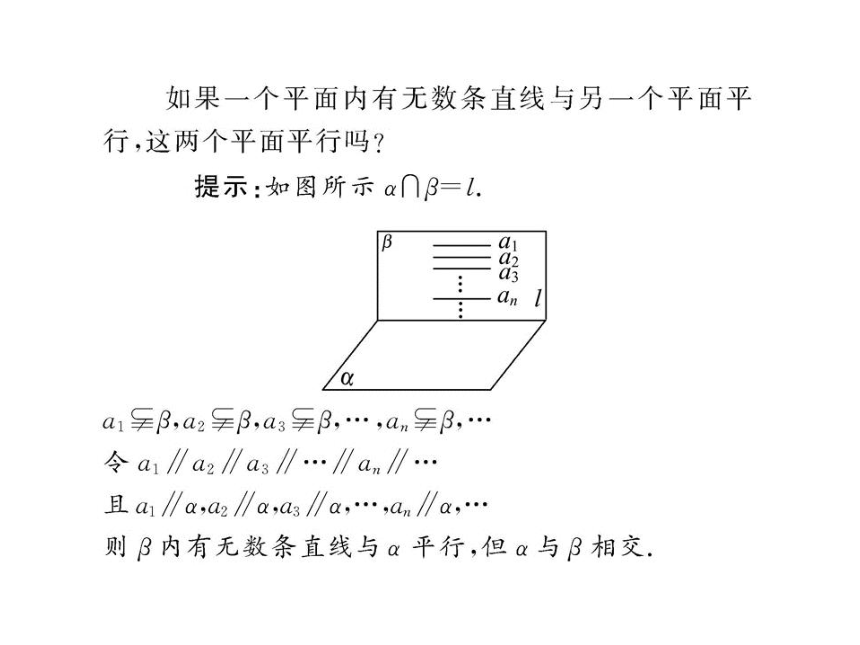
∴AB1∥平面BEC1.1.对面面平行判定定理的理解
(1)本质:证面面平行 证线面平行.
(2)核心问题“线不在多,两条就行”,也就是说要求一个平面内有两条相交直线与另一个平面平行,不是两条平行直线,也不是无数条直线.平面与平面平行的判定2.面面平行的其他证法
(1)一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行.
(2)如果两个平面同时平行于第三个平面,那么这两个平面平行.【例2】 如图所示,在正方体ABCD
-A1B1C1D1中,E、F、M、N分别是AB、
CC1、AA1、C1D1的中点,
求证:平面CEM∥平面BFN.
【审题指导】由题意,可知平面CEM和平面BFN与正方体的交线没有完全画出,易证ME∥NF,进一步可得ME∥平面BFN.因此,解答本题的关键是将平面BFN与正方体的交线画出,并证明EC∥平面BFN.【规范解答】如图,取A1B1的中点G,
连接GE、A1N、A1B、CD1,GC1
由题意,得NF∥CD1,又CD1∥A1B
∴NF∥A1B∴A1、N、F、B共面
又M、E分别为AA1、AB的中点,
∴ME∥A1B,∴ME∥NF
又ME 平面A1BFN,NF 平面A1BFN
∴ME∥平面A1BFN又GE∥CC1且GE=CC1,
∴四边形CC1GE是平行四边形,∴EC∥C1G.
又N、G分别为C1D1、A1B1的中点,∴ NC1 A1G,
∴四边形A1GC1N是平行四边形
∴A1N∥C1G,∴EC∥A1N
EC 平面A1BFN,A1N 平面A1BFN
∴EC∥平面A1BFN,又EC∩ME=E
∴ 平面A1BFN∥平面CEM
即平面CEM∥平面BFN.【变式训练】如图,在正方体ABCD-
A1B1C1D1中,E、F、G分别是CB、CD、
CC1的中点,求证:平面AB1D1∥平面
EFG.
【解题提示】解答本题可利用正方体的结构特征和平行四边形的性质证明EF∥平面AB1D1,EG∥平面AB1D1 .【证明】如图,连接BD.∵E、F分别为BC、CD的中点,
∴EF∥BD,又BD B1D1,
∴EF∥B1D1,
又∵EF? 平面AB1D1,
B1D1 平面AB1D1,
∴EF∥平面AB1D1,
同理可得EG∥平面AB1D1,
又∵EF∩EG=E,EF、EG 平面EFG,
∴平面EFG∥平面AB1D1.1. 对探索性问题的认识:
探索性问题常常需要由给定的题设条件去探索相应的结论,或由问题的结论去追溯相应的条件,要求在解题之前必须透过问题的表象去寻找、去发现规律性的东西.此类问题增加了许多可变的因素,思维指向不明显,解题时往往难以下手.探索性问题 2.探索性问题主要有以下几类:
(1)探索条件型问题:从给定的问题结论出发,追溯结论成立的条件;
(2)探索结论型问题:从给定的题设条件出发,探求相关的结论;
(3)探索存在型问题:从假设相关结论存在出发,从而肯定或否定这种结论存在性;
(4)探索综合型问题:从变更题设条件或问题的结论的某个部分出发,探究问题的相应变化.【例3】如图
所示,在正方体ABCD-A1B1C1D1中,E
是棱DD1的中点.在棱C1D1上是否存在
一点F,使B1F∥平面A1BE?证明你的
结论.
【审题指导】本题属于探索存在型问题,可以先假设在棱C1D1上存在一点F,使B1F∥平面A1BE,在此条件下根据线面平行的判定定理确定B1F与平面A1BE中哪条直线平行,进一步确定点F的位置.【规范解答】在棱C1D1上存在点F,
使B1F∥平面A1BE.
分别取C1D1和CD的中点F,G,
连接EG,BG,CD1,FG,B1F.因A1D1∥B1C1∥BC,且A1D1=BC,
所以四边形A1BCD1是平行四边形,
因此D1C∥A1B.又E,G分别为D1D,CD的中点,
所以EG∥D1C,从而EG∥A1B.这说明A1,B,G,E共面.所以BG 平面A1BE.
因四边形C1CDD1与B1BCC1都为正方形,
F,G分别为C1D1和CD的中点,所以FG∥C1C∥B1B,且FG=C1C=B1B,
因此四边形B1BGF是平行四边形,
所以B1F∥BG.而B1F 平面A1BE ,BG 平面A1BE,
故B1F∥平面A1BE.【变式训练】如图,在四棱锥P-
ABCD中,过BD且与PA平行的截面
是否存在?这样的截面有几个,
应如何作出?
【解题提示】解答本题的关键是选择恰当的平面,过恰当的点作直线PA的平行线.【解析】过BD有且只有一个与PA平行的截面.
画法:(1)连接AC交BD于点O
(2)在△PAC中,过点O作OE∥PA,交PC于点E
(3)连接BE、DE
△BDE即为所求作截面
(如图所示).
由画法中点E的唯一性知
这样的截面是唯一的.【典例】(12分)已知在△ABC中,
D、E分别为AC、AB的中点,沿DE
将△ADE折起,M是PB的中点.
求证:ME∥平面PCD.
【审题指导】由题意得DE∥BC且 在折叠后仍然成立,可以利用这一信息,在△PBC中过PB的中点M作出BC的平行线,构成平行四边形,在平面PCD中找到ME平行的直线.【规范解答】过M作MF∥BC,交PC于点F,
连接DF, …………………………………………………2分
又∵M为PB的中点,∴F为CP的中点,
……………………………………………4分
又∵D、E分别为AC、AB的中点,
∴DE∥BC且 …………………………………6分
∴DE∥MF且DE=MF,∴四边形DEMF是平行四边形, ……………………………8分
∴ME∥FD. ………………………………………………10分
又∵ME 平面PCD,FD 平面PCD,
∴ME∥平面PCD. ………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】如图所示,已知四边形
ABCD是正方形,四边形ACEF是矩形,
AB=2,AF=1,M是线段EF的中点,
求证:AM∥平面BDE.【证明】记AC与BD的交点为O,连接OE.
∵O、M分别是AC、EF的中点,四边形ACEF是矩形
∴OA∥EM 且OA=EM
∴四边形AOEM是平行四边形.
∴AM∥OE
∵OE 平面BDE,
AM? 平面BDE
∴AM∥平面BDE.1.能保证直线a与平面α平行的条件是( )
(A) a? α,b α,a∥b
(B) B α,a∥b
(C) b α,c α,a∥c且a∥b
(D) B α,A∈a,B∈a,C∈b,D∈b,且AC=BD
【解析】选A.根据线面平行的判定定理可知A正确.
对于B、C都有a α的可能. 对于D有可能A、B在平面α的
异侧.2.a,b α,a∥β,b∥β, 下列说法正确的是( )
(A)若a与b相交,则α与β相交
(B)若a与b相交,则α∥β
(C)若a∥b,则α与β相交
(D)若a∥b,则α∥β
【解析】选B.根据面面平行的判定定理可知B正确.3.正六棱柱的底面和侧面中互相平行的面有( )
(A)1对 (B)2对 (C)3对 (D)4对
【解析】选D.正六棱柱中除了两个底面平行外,侧面中有3对互相平行的平面.4.如图所示,在正方体ABCD-A1B1C1D1
中 ,E是AB的中点,则和平面C1D1E
平行的棱为__________.
【解析】在正方体ABCD-A1B1C1D1 中 ,
因为CD∥C1D1且CD 平面C1D1E,所以CD∥平面C1D1E,同理可得A1B1∥平面C1D1E.
答案:CD和A1B15.如图,在长方体ABCD-
A′B′C′D′中,
(1)与直线CD平行的平面
是_______________
(2)与直线CC′平行的平面是______________
(3)与直线CB平行的平面是_______________
(4)与直线AC平行的平面是_______________
(5)与直线AD′平行的平面是_______________
(6)与直线AB′平行的平面是_______________【解析】利用长方体的性质和线面平行的判定定理解答.
答案:(1)平面A′C′,平面A′B
(2)平面A′B,平面A′D
(3)平面A′D,平面A′C′
(4)平面A′C′
(5)平面BC′
(6)平面C′D6.如图 ,在几何体ABC –
A′B′C′中,∠1+∠2= 180°,
∠3+∠4= 180°,求证:平面ABC ∥
平面A′B′C′.【证明】在四边形ABB′A′中,
∵∠1+∠2=180°,
∴A′B′∥AB.
又∵A′B′? 平面ABC,AB 平面ABC ,
∴A′B′∥平面ABC.
同理可证B′C′∥平面ABC.
又∵A′B′∩B′C′=B′,
∴平面ABC∥平面A′B′C′.一、选择题(每题4分,共16分)
1.若直线l不平行于平面α,且l α,则( )
(A)α内的所有直线与l异面
(B)α内不存在与l平行的直线
(C)α内存在唯一的直线与l平行
(D)α内的直线与l都相交【解析】选B.由题意可得直线l与平面α相交,如图:对A,由于α内的所有不过交点的直线与l异面,故A错误;对B,如果α内存在与l平行的直线,则直线l与α平行,故直线不存在,故B正确;对C,可得直线l与α平行,与题设不符,故C错误;对D,α内的所有不过交点的直线与l异面,故D错误.2.平面α与平面β平行的条件可以是( )
(A)α内有无穷多条直线都与β平行
(B)直线a∥α,a∥β,且直线a不在α与β内
(C)直线a α,直线b β,且b∥α,a∥β
(D)α内的任何直线都与β平行【解析】选D.对于A项,若α与β相交时,α内也有无数条直线都与交线平行,即α内有无数条直线与β平行,故A错.
对于B项,若a平行于α与β的交线时,也能满足,但此时α与β相交,故B错.
对于C项,若a和b都与α与β的交线平行时,也能满足,但此时α与β相交,故C错.
对于D项,α内的任何直线都与β平行,故在一个平面内存在两条相交直线平行于另一个平面,故D正确.3.在正方体ABCD-A1B1C1D1 中,下列四对截面中彼此平行的一对截面是( )
(A)A1BC1与ACD1 (B)BDC1与B1D1C
(C)B1D1D与BDA1 (D)ADC1与AD1C【解析】选A.如图所示,平面A1BC1与平面ACD1平行.4.正方体ABCD-A1B1C1D1的棱长为1,
E是AB的中点,点F在BC上,则BF等
于多少时,EF∥平面A1C1D.( )【解析】选B.当点F是BC的中点时,即
有EF∥平面A1C1D.
∵EF∥AC,AC∥A1C1,
∴EF∥A1C1,
又∵EF? 平面A1C1D,A1C1 平面A1C1D,
∴EF∥平面A1C1D.二、填空题(每题4分,共8分)
5. 如图,在空间四边形ABCD中,M∈AB,
N∈AD, 若 则直线MN与平面
BDC的位置关系是__________.
【解析】在平面ABD内,
∴MN∥BD.
又MN ?平面BCD,BD 平面BCD,
∴MN∥平面BCD.
答案:平行6. 若直线a, b相交,且a∥α ,则b与平面α的位置关系是__________.
【解析】b与平面α相交或平行
答案:相交或平行三、解答题(每题8分,共16分)
7.如图所示,已知A1B1C1-ABC
是正三棱柱,E、E1分别是AC、
A1C1的中点,求证:平面AB1E1
∥平面BEC1.
【解题提示】先证明四边形BB1E1E、AEC1E1是平行四边形,再证明BE∥平面AB1E1,C1E∥平面AB1E1,最后用面面平行的判定定理证明平面AB1E1∥平面BEC1.【证明】连接EE1,
∵四边形AA1C1C是矩形且点E、E1分别是AC、A1C1的中点,
∴EC∥E1C1且EC=E1C1,
∴四边形ECC1E1是平行四边形,
∴EE1∥CC1且EE1=CC1,
又BB1∥CC1且BB1=CC1,
∴四边形BB1E1E是平行四边形,
∴BE∥B1E1,又BE 平面AB1E1,B1E1 平面AB1E1,
∴BE∥平面AB1E1.
∵四边形AEC1E1是平行四边形,
∴C1E∥AE1,
又C1E 平面AB1E1,AE1 平面AB1E1,
∴C1E∥平面AB1E1,
又BE∩C1E=E,
∴平面AB1E1∥平面BEC1.8.如图是一几何体的直观图,主视图和俯视图.(1)在主视图右侧,按照画三视图的要求画出该几何体的左视图;
(2)在所给直观图中连接BD,证明:BD∥面PEC;【解析】(1)如图所示(2)取PC的中点M,设AC与BD的交点为N,
连接MN,ME,
∵PM=CM,AN=CN,
MN∥PA,
∴MN=EB,MN∥EB.
故BEMN是平行四边形,
∴EM∥BN,又EM 平面PEC,BD 平面PEC,
∴BD∥平面PEC. 【方法技巧】找线线平行的诀窍
用线面平行的判定定理证明线面平行时,关键是找“线线平行”,即找平面内一条直线与平面外一条直线平行.找线线平行的常用方法有如下几种:
(1)用空间直线平行关系的传递性
(2)用三角形中位线的性质
(3)用平行四边形对边平行的性质
(4)用平行线分线段成比例定理的有关知识【挑战能力】
(10分)如图:在四棱锥P-ABCD中,
底面ABCD是平行四边形,点M、N
分别为BC、PA的中点,在线段PD
上是否存在一点E,使得NM∥平面
ACE;若存在,说明点E的位置;
若不存在,说明理由.【解析】存在.取PD的中点E,
连接NE,EC,AE,因为N、E分
别为PA,PD的中点,所以NE∥AD
且 又在平行四边形ABCD
中,CM∥AD且
所以NE MC,即四边形MCEN是平行四边形,所以NM∥EC,
又EC 平面ACE,NM 平面ACE,所以MN∥平面ACE,
即在PD上存在一点E,使得NM∥平面ACE,
此时
(1)直线a不在平面α内,即a α.
(2)直线b在平面α内,即b α.
(3)两条直线a、b平行,即a∥b.
要注意线面平行关系不具有传递性,即
如果a∥b,a∥α,那么b与α不一定平行.实际上,此时有
B α和b∥α两种情况.【例1】在正方体ABCD-A1B1C1D1中,
E、F 分别为棱BC、C1D1 的中点.
求证:EF∥平面BB1D1D.
【审题指导】在平面BB1D1D内找到一条直线与直线EF平行是证明本题的关键,根据图形中直线与平面的位置关系,可考虑用平行四边形的性质作辅助线证明.【规范解答】连接AC交BD于点O,连接OE,OD1,
则OE∥DC,
∵ DC∥D1C1, DC=D1C1,
F 为D1C1的中点,
∴ OE∥D1F, OE =D1F,
∴ 四边形D1FEO 为平行四边形.
∴ EF∥D1O.
又∵ EF 平面BB1D1D,D1O 平面BB1D1D,
∴ EF∥平面BB1D1D.【变式训练】如图,P是平行四边形
ABCD所在平面外一点,Q是PA的中点,
试判断PC与平面BDQ的关系,并证明.【解析】PC∥平面BDQ.证明如下:
连接AC,交BD于点O,连接OQ
∵四边形ABCD是平行四边形
∴O为AC的中点.
又∵Q是PA的中点,
∴OQ∥PC.
又∵PC 平面BDQ,OQ 平面BDQ,
∴PC∥平面BDQ. 【误区警示】解答本题的过程中易漏掉条件PC 平
面BDQ及OQ 平面BDQ,在利用线面平行的判定定理证明线
面平行时,定理中的三个条件缺一不可.【例】如图,四边形ABCD,ADEF都是
正方形,M∈BD,N∈AE,且BM=AN.
求证:MN∥平面CED.
【审题指导】要证MN∥平面CED,就要在平面CED内找一条直线与直线MN平行,可以用以下两个办法:(1)连接AM并延长与CD相交,在三角形中寻找线线平行;(2)分别过点M、N作AD的平行线,利用平行四边形的性质寻找线线平行.【规范解答】方法一:如图(1),连接
AM并延长交CD于点G,连接GE,
因为AB∥CD,所以
所以
即又因为BD=AE且AN=BM,
所以
所以MN∥GE,
又GE 平面CED,
MN 平面CED,
所以MN∥平面CED.方法二:如图(2),
过点M在平面ABCD中作MS∥AD交CD于点S,过点N在平面ADEF中作NT∥AD交DE于点T,连接ST.
因为MS∥AD,AD∥BC,
所以MS∥BC,
所以
因为BM=AN,BD=AE,所以BD-BM=AE-AN,即DM=EN.所以
又因为NT∥AD,
所以 所以
因为AD=BC,所以MS=NT.
又因为MS∥AD,NT∥AD,所以MS∥NT,
所以四边形MSTN为平行四边形,所以MN∥ST.
又因为MN 平面CED,ST 平面CED,
所以MN∥平面CED.【变式备选】
如图所示,三棱柱ABC—A1B1C1中,E是AC的中点,求证:AB1∥平面BEC1.【证明】连接B1C交BC1于O点,
则O为B1C的中点,连接EO,
平面AB1C∩平面BEC1=EO,
在△AB1C中,EO为△AB1C的
中位线,∴AB1∥EO,
又∵AB1 平面BEC1,
EO 平面BEC1,
∴AB1∥平面BEC1.1.对面面平行判定定理的理解
(1)本质:证面面平行 证线面平行.
(2)核心问题“线不在多,两条就行”,也就是说要求一个平面内有两条相交直线与另一个平面平行,不是两条平行直线,也不是无数条直线.平面与平面平行的判定2.面面平行的其他证法
(1)一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行.
(2)如果两个平面同时平行于第三个平面,那么这两个平面平行.【例2】 如图所示,在正方体ABCD
-A1B1C1D1中,E、F、M、N分别是AB、
CC1、AA1、C1D1的中点,
求证:平面CEM∥平面BFN.
【审题指导】由题意,可知平面CEM和平面BFN与正方体的交线没有完全画出,易证ME∥NF,进一步可得ME∥平面BFN.因此,解答本题的关键是将平面BFN与正方体的交线画出,并证明EC∥平面BFN.【规范解答】如图,取A1B1的中点G,
连接GE、A1N、A1B、CD1,GC1
由题意,得NF∥CD1,又CD1∥A1B
∴NF∥A1B∴A1、N、F、B共面
又M、E分别为AA1、AB的中点,
∴ME∥A1B,∴ME∥NF
又ME 平面A1BFN,NF 平面A1BFN
∴ME∥平面A1BFN又GE∥CC1且GE=CC1,
∴四边形CC1GE是平行四边形,∴EC∥C1G.
又N、G分别为C1D1、A1B1的中点,∴ NC1 A1G,
∴四边形A1GC1N是平行四边形
∴A1N∥C1G,∴EC∥A1N
EC 平面A1BFN,A1N 平面A1BFN
∴EC∥平面A1BFN,又EC∩ME=E
∴ 平面A1BFN∥平面CEM
即平面CEM∥平面BFN.【变式训练】如图,在正方体ABCD-
A1B1C1D1中,E、F、G分别是CB、CD、
CC1的中点,求证:平面AB1D1∥平面
EFG.
【解题提示】解答本题可利用正方体的结构特征和平行四边形的性质证明EF∥平面AB1D1,EG∥平面AB1D1 .【证明】如图,连接BD.∵E、F分别为BC、CD的中点,
∴EF∥BD,又BD B1D1,
∴EF∥B1D1,
又∵EF? 平面AB1D1,
B1D1 平面AB1D1,
∴EF∥平面AB1D1,
同理可得EG∥平面AB1D1,
又∵EF∩EG=E,EF、EG 平面EFG,
∴平面EFG∥平面AB1D1.1. 对探索性问题的认识:
探索性问题常常需要由给定的题设条件去探索相应的结论,或由问题的结论去追溯相应的条件,要求在解题之前必须透过问题的表象去寻找、去发现规律性的东西.此类问题增加了许多可变的因素,思维指向不明显,解题时往往难以下手.探索性问题 2.探索性问题主要有以下几类:
(1)探索条件型问题:从给定的问题结论出发,追溯结论成立的条件;
(2)探索结论型问题:从给定的题设条件出发,探求相关的结论;
(3)探索存在型问题:从假设相关结论存在出发,从而肯定或否定这种结论存在性;
(4)探索综合型问题:从变更题设条件或问题的结论的某个部分出发,探究问题的相应变化.【例3】如图
所示,在正方体ABCD-A1B1C1D1中,E
是棱DD1的中点.在棱C1D1上是否存在
一点F,使B1F∥平面A1BE?证明你的
结论.
【审题指导】本题属于探索存在型问题,可以先假设在棱C1D1上存在一点F,使B1F∥平面A1BE,在此条件下根据线面平行的判定定理确定B1F与平面A1BE中哪条直线平行,进一步确定点F的位置.【规范解答】在棱C1D1上存在点F,
使B1F∥平面A1BE.
分别取C1D1和CD的中点F,G,
连接EG,BG,CD1,FG,B1F.因A1D1∥B1C1∥BC,且A1D1=BC,
所以四边形A1BCD1是平行四边形,
因此D1C∥A1B.又E,G分别为D1D,CD的中点,
所以EG∥D1C,从而EG∥A1B.这说明A1,B,G,E共面.所以BG 平面A1BE.
因四边形C1CDD1与B1BCC1都为正方形,
F,G分别为C1D1和CD的中点,所以FG∥C1C∥B1B,且FG=C1C=B1B,
因此四边形B1BGF是平行四边形,
所以B1F∥BG.而B1F 平面A1BE ,BG 平面A1BE,
故B1F∥平面A1BE.【变式训练】如图,在四棱锥P-
ABCD中,过BD且与PA平行的截面
是否存在?这样的截面有几个,
应如何作出?
【解题提示】解答本题的关键是选择恰当的平面,过恰当的点作直线PA的平行线.【解析】过BD有且只有一个与PA平行的截面.
画法:(1)连接AC交BD于点O
(2)在△PAC中,过点O作OE∥PA,交PC于点E
(3)连接BE、DE
△BDE即为所求作截面
(如图所示).
由画法中点E的唯一性知
这样的截面是唯一的.【典例】(12分)已知在△ABC中,
D、E分别为AC、AB的中点,沿DE
将△ADE折起,M是PB的中点.
求证:ME∥平面PCD.
【审题指导】由题意得DE∥BC且 在折叠后仍然成立,可以利用这一信息,在△PBC中过PB的中点M作出BC的平行线,构成平行四边形,在平面PCD中找到ME平行的直线.【规范解答】过M作MF∥BC,交PC于点F,
连接DF, …………………………………………………2分
又∵M为PB的中点,∴F为CP的中点,
……………………………………………4分
又∵D、E分别为AC、AB的中点,
∴DE∥BC且 …………………………………6分
∴DE∥MF且DE=MF,∴四边形DEMF是平行四边形, ……………………………8分
∴ME∥FD. ………………………………………………10分
又∵ME 平面PCD,FD 平面PCD,
∴ME∥平面PCD. ………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】如图所示,已知四边形
ABCD是正方形,四边形ACEF是矩形,
AB=2,AF=1,M是线段EF的中点,
求证:AM∥平面BDE.【证明】记AC与BD的交点为O,连接OE.
∵O、M分别是AC、EF的中点,四边形ACEF是矩形
∴OA∥EM 且OA=EM
∴四边形AOEM是平行四边形.
∴AM∥OE
∵OE 平面BDE,
AM? 平面BDE
∴AM∥平面BDE.1.能保证直线a与平面α平行的条件是( )
(A) a? α,b α,a∥b
(B) B α,a∥b
(C) b α,c α,a∥c且a∥b
(D) B α,A∈a,B∈a,C∈b,D∈b,且AC=BD
【解析】选A.根据线面平行的判定定理可知A正确.
对于B、C都有a α的可能. 对于D有可能A、B在平面α的
异侧.2.a,b α,a∥β,b∥β, 下列说法正确的是( )
(A)若a与b相交,则α与β相交
(B)若a与b相交,则α∥β
(C)若a∥b,则α与β相交
(D)若a∥b,则α∥β
【解析】选B.根据面面平行的判定定理可知B正确.3.正六棱柱的底面和侧面中互相平行的面有( )
(A)1对 (B)2对 (C)3对 (D)4对
【解析】选D.正六棱柱中除了两个底面平行外,侧面中有3对互相平行的平面.4.如图所示,在正方体ABCD-A1B1C1D1
中 ,E是AB的中点,则和平面C1D1E
平行的棱为__________.
【解析】在正方体ABCD-A1B1C1D1 中 ,
因为CD∥C1D1且CD 平面C1D1E,所以CD∥平面C1D1E,同理可得A1B1∥平面C1D1E.
答案:CD和A1B15.如图,在长方体ABCD-
A′B′C′D′中,
(1)与直线CD平行的平面
是_______________
(2)与直线CC′平行的平面是______________
(3)与直线CB平行的平面是_______________
(4)与直线AC平行的平面是_______________
(5)与直线AD′平行的平面是_______________
(6)与直线AB′平行的平面是_______________【解析】利用长方体的性质和线面平行的判定定理解答.
答案:(1)平面A′C′,平面A′B
(2)平面A′B,平面A′D
(3)平面A′D,平面A′C′
(4)平面A′C′
(5)平面BC′
(6)平面C′D6.如图 ,在几何体ABC –
A′B′C′中,∠1+∠2= 180°,
∠3+∠4= 180°,求证:平面ABC ∥
平面A′B′C′.【证明】在四边形ABB′A′中,
∵∠1+∠2=180°,
∴A′B′∥AB.
又∵A′B′? 平面ABC,AB 平面ABC ,
∴A′B′∥平面ABC.
同理可证B′C′∥平面ABC.
又∵A′B′∩B′C′=B′,
∴平面ABC∥平面A′B′C′.一、选择题(每题4分,共16分)
1.若直线l不平行于平面α,且l α,则( )
(A)α内的所有直线与l异面
(B)α内不存在与l平行的直线
(C)α内存在唯一的直线与l平行
(D)α内的直线与l都相交【解析】选B.由题意可得直线l与平面α相交,如图:对A,由于α内的所有不过交点的直线与l异面,故A错误;对B,如果α内存在与l平行的直线,则直线l与α平行,故直线不存在,故B正确;对C,可得直线l与α平行,与题设不符,故C错误;对D,α内的所有不过交点的直线与l异面,故D错误.2.平面α与平面β平行的条件可以是( )
(A)α内有无穷多条直线都与β平行
(B)直线a∥α,a∥β,且直线a不在α与β内
(C)直线a α,直线b β,且b∥α,a∥β
(D)α内的任何直线都与β平行【解析】选D.对于A项,若α与β相交时,α内也有无数条直线都与交线平行,即α内有无数条直线与β平行,故A错.
对于B项,若a平行于α与β的交线时,也能满足,但此时α与β相交,故B错.
对于C项,若a和b都与α与β的交线平行时,也能满足,但此时α与β相交,故C错.
对于D项,α内的任何直线都与β平行,故在一个平面内存在两条相交直线平行于另一个平面,故D正确.3.在正方体ABCD-A1B1C1D1 中,下列四对截面中彼此平行的一对截面是( )
(A)A1BC1与ACD1 (B)BDC1与B1D1C
(C)B1D1D与BDA1 (D)ADC1与AD1C【解析】选A.如图所示,平面A1BC1与平面ACD1平行.4.正方体ABCD-A1B1C1D1的棱长为1,
E是AB的中点,点F在BC上,则BF等
于多少时,EF∥平面A1C1D.( )【解析】选B.当点F是BC的中点时,即
有EF∥平面A1C1D.
∵EF∥AC,AC∥A1C1,
∴EF∥A1C1,
又∵EF? 平面A1C1D,A1C1 平面A1C1D,
∴EF∥平面A1C1D.二、填空题(每题4分,共8分)
5. 如图,在空间四边形ABCD中,M∈AB,
N∈AD, 若 则直线MN与平面
BDC的位置关系是__________.
【解析】在平面ABD内,
∴MN∥BD.
又MN ?平面BCD,BD 平面BCD,
∴MN∥平面BCD.
答案:平行6. 若直线a, b相交,且a∥α ,则b与平面α的位置关系是__________.
【解析】b与平面α相交或平行
答案:相交或平行三、解答题(每题8分,共16分)
7.如图所示,已知A1B1C1-ABC
是正三棱柱,E、E1分别是AC、
A1C1的中点,求证:平面AB1E1
∥平面BEC1.
【解题提示】先证明四边形BB1E1E、AEC1E1是平行四边形,再证明BE∥平面AB1E1,C1E∥平面AB1E1,最后用面面平行的判定定理证明平面AB1E1∥平面BEC1.【证明】连接EE1,
∵四边形AA1C1C是矩形且点E、E1分别是AC、A1C1的中点,
∴EC∥E1C1且EC=E1C1,
∴四边形ECC1E1是平行四边形,
∴EE1∥CC1且EE1=CC1,
又BB1∥CC1且BB1=CC1,
∴四边形BB1E1E是平行四边形,
∴BE∥B1E1,又BE 平面AB1E1,B1E1 平面AB1E1,
∴BE∥平面AB1E1.
∵四边形AEC1E1是平行四边形,
∴C1E∥AE1,
又C1E 平面AB1E1,AE1 平面AB1E1,
∴C1E∥平面AB1E1,
又BE∩C1E=E,
∴平面AB1E1∥平面BEC1.8.如图是一几何体的直观图,主视图和俯视图.(1)在主视图右侧,按照画三视图的要求画出该几何体的左视图;
(2)在所给直观图中连接BD,证明:BD∥面PEC;【解析】(1)如图所示(2)取PC的中点M,设AC与BD的交点为N,
连接MN,ME,
∵PM=CM,AN=CN,
MN∥PA,
∴MN=EB,MN∥EB.
故BEMN是平行四边形,
∴EM∥BN,又EM 平面PEC,BD 平面PEC,
∴BD∥平面PEC. 【方法技巧】找线线平行的诀窍
用线面平行的判定定理证明线面平行时,关键是找“线线平行”,即找平面内一条直线与平面外一条直线平行.找线线平行的常用方法有如下几种:
(1)用空间直线平行关系的传递性
(2)用三角形中位线的性质
(3)用平行四边形对边平行的性质
(4)用平行线分线段成比例定理的有关知识【挑战能力】
(10分)如图:在四棱锥P-ABCD中,
底面ABCD是平行四边形,点M、N
分别为BC、PA的中点,在线段PD
上是否存在一点E,使得NM∥平面
ACE;若存在,说明点E的位置;
若不存在,说明理由.【解析】存在.取PD的中点E,
连接NE,EC,AE,因为N、E分
别为PA,PD的中点,所以NE∥AD
且 又在平行四边形ABCD
中,CM∥AD且
所以NE MC,即四边形MCEN是平行四边形,所以NM∥EC,
又EC 平面ACE,NM 平面ACE,所以MN∥平面ACE,
即在PD上存在一点E,使得NM∥平面ACE,
此时
