1.5.2 平面与平面平行的性质 课件2
文档属性
| 名称 | 1.5.2 平面与平面平行的性质 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 784.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-22 14:13:10 | ||
图片预览



文档简介
课件18张PPT。1.5.2 平面与平面平行的性质1、使学生掌握平面与平面平行的性质,并会应用性质解决问题.
2、理解直线与直线、直线与平面、平面与平面之间的位置关系可以相互转化.
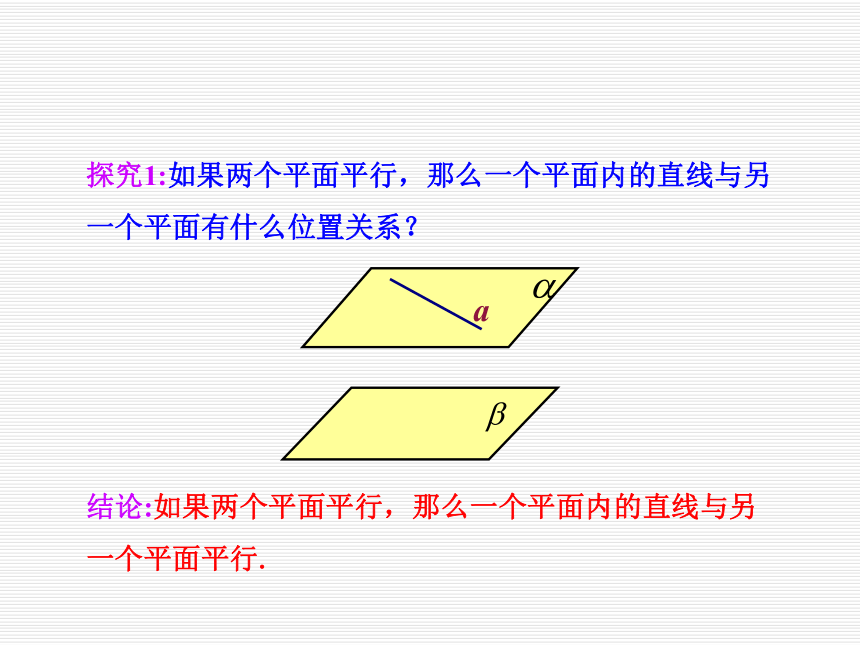
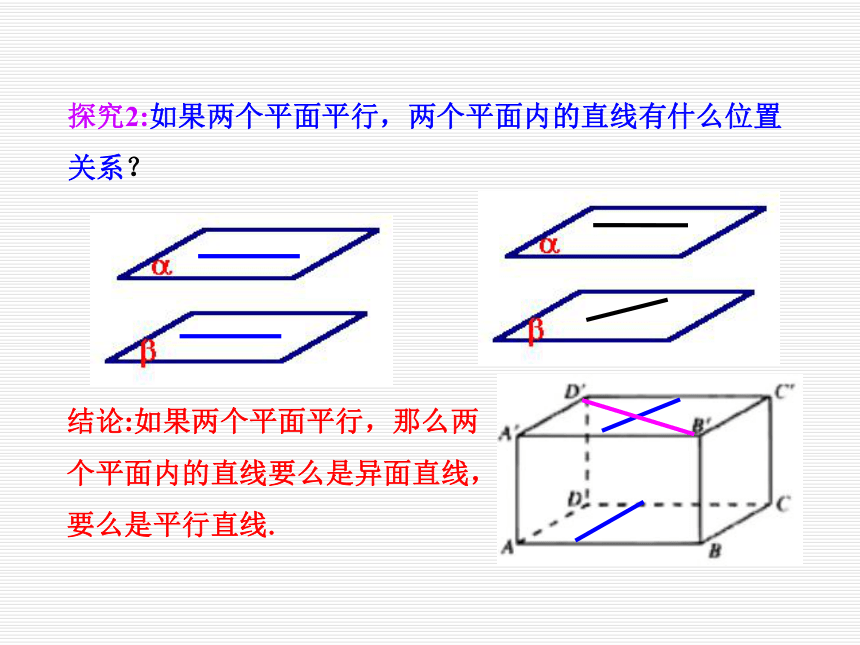
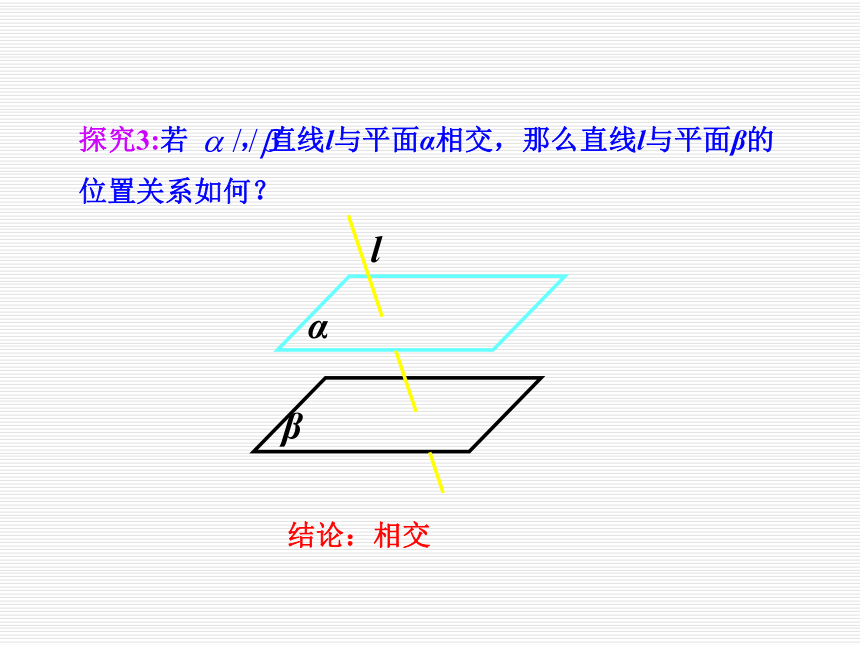
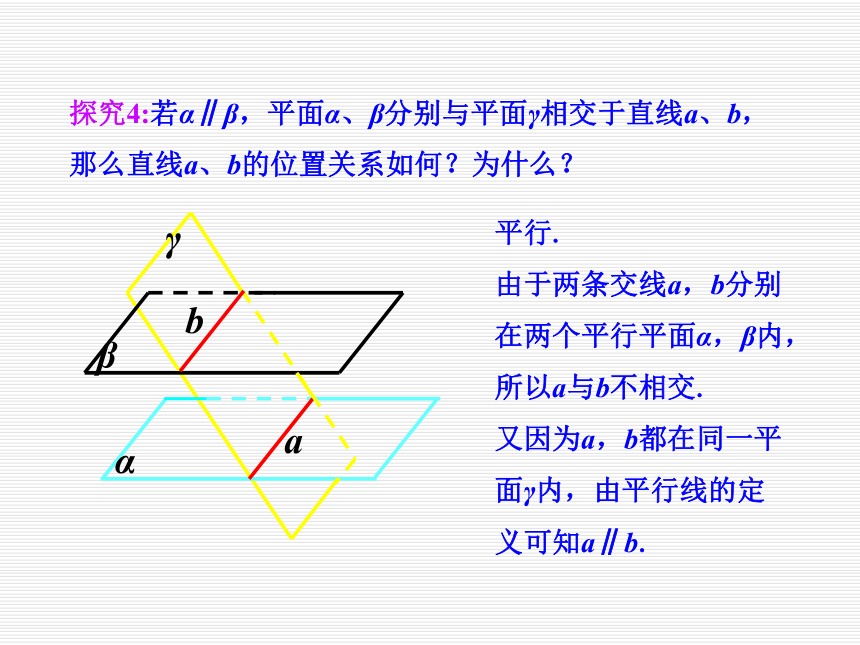
3、让学生在发现中学习,增强学习的积极性;让学生了解空间与平面互相转换的数学思想.回想一下,平面与平面的判定定理是什么? 平面与平面的判定定理解决了平面与平面平行的条件问题,反之,在平面与平面平行的条件下,可以得到什么结论呢?探究1:如果两个平面平行,那么一个平面内的直线与另一个平面有什么位置关系?结论:如果两个平面平行,那么一个平面内的直线与另一个平面平行.探究2:如果两个平面平行,两个平面内的直线有什么位置关系?结论:如果两个平面平行,那么两个平面内的直线要么是异面直线,要么是平行直线.探究3:若 ,直线l与平面α相交,那么直线l与平面β的位置关系如何?结论:相交探究4:若α∥β,平面α、β分别与平面γ相交于直线a、b,那么直线a、b的位置关系如何?为什么?平行.
由于两条交线a,b分别在两个平行平面α,β内,所以a与b不相交.
又因为a,b都在同一平面γ内,由平行线的定义可知a∥b.探究5:综上分析,在平面与平面平行的条件下可以得到什么结论?并用文字语言表述之. 定理5.4 如果两个平行平面同时和第三个平面相交,那么它们的交线平行. 上述定理通常称为平面与平面平行的性质定理,该定理用符号语言可怎样表述?a//b想一想:平面与平面平行的性质定理可简述为“面面平行,则线线平行”,在实际应用中它有何功能作用?功能作用:可以由平面与平面平行得出直线与直线平行.平面和平面平行的判定定理:直线与直线平行平面与平面平行平面和平面平行的性质定理结论:1、若两个平面互相平行,则其中一个平面中的直线必平行于另一个平面;
2、平行于同一平面的两平面平行;
3、过平面外一点有且只有一个平面与这个平面平行;
4、夹在两平行平面间的平行线段相等.例1.?求证:夹在两个平行平面间的平行线段相等.如图,α//β,AB//CD,且A∈α,
C∈α,B∈β,D∈β.
求证:AB=CD.证明 因为AB//CD,所以过AB,CD可作平面γ,且平面γ与平面α和β分别相交于AC和BD.因为α//β,所以BD//AC.因此,四边形ABDC是平行四边形.所以AB=CD.例2 如图,平面α,β,γ两两平行,且直线l与α,β,γ分别交于点A,B,C,直线m与α,β,γ分别交于点D,E,F,AB=6,BC=2,EF=3.求DE的长.解 当直线m与l共面时,该平面与α,β,γ分别交于直线AD,BE,CF,因为α,β,γ两两平行,所以AD∥BE
∥CF,故当直线m与l不共面时,连接DC.
设DC与β相交于点G,则平面ACD与α,β分别相交于直线AD,BG,平面DCF与β,γ分别交于直线GE,CF.因为α,β,γ两两平行,所以BG∥ AD,GE∥CF.
因此所以 又因为AB=6,BC=2,EF=3,所以,DE=9.1、设平面α∥平面β,A∈α,B∈β,C是AB的中点,当
A、B分别在α、β内运动时,那么所有的动点C( )A.不共面;
B.当且仅当A、B在两条相交直线上移动时才共面;
C.当且仅当A、B在两条给定的平行直线上移动时才共面;
D.不论A、B如何移动都共面.D2.过长方体ABCD-A1B1C1D1的任意两条棱的中点作直线,
其中能够与平面ACC1A1平行的直线有________条.【解析】如图,与AC平行的直线有4条,与AA1平行的直线有4条,连接MN,则MN∥面ACC1A1,这样的直线也有4条(包括MN).123.正方体ABCD-A1B1C1D1中,E、M、F为棱B1C1,C1D1和B1B的中点,试过E、M作一平面与平面A1FC平行.解 如图,取CC1中点G,连接B1G,取C1G中点H,连接EH.则EH∥B1G∥FC.
同理,连接MH.则MH∥A1F.
连接EM,
又MH∩EH=H,
∴面EMH∥面A1FC,
即面EHM为所求平面. 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.面面平行的判定定理面面平行的性质定理 如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
2、理解直线与直线、直线与平面、平面与平面之间的位置关系可以相互转化.
3、让学生在发现中学习,增强学习的积极性;让学生了解空间与平面互相转换的数学思想.回想一下,平面与平面的判定定理是什么? 平面与平面的判定定理解决了平面与平面平行的条件问题,反之,在平面与平面平行的条件下,可以得到什么结论呢?探究1:如果两个平面平行,那么一个平面内的直线与另一个平面有什么位置关系?结论:如果两个平面平行,那么一个平面内的直线与另一个平面平行.探究2:如果两个平面平行,两个平面内的直线有什么位置关系?结论:如果两个平面平行,那么两个平面内的直线要么是异面直线,要么是平行直线.探究3:若 ,直线l与平面α相交,那么直线l与平面β的位置关系如何?结论:相交探究4:若α∥β,平面α、β分别与平面γ相交于直线a、b,那么直线a、b的位置关系如何?为什么?平行.
由于两条交线a,b分别在两个平行平面α,β内,所以a与b不相交.
又因为a,b都在同一平面γ内,由平行线的定义可知a∥b.探究5:综上分析,在平面与平面平行的条件下可以得到什么结论?并用文字语言表述之. 定理5.4 如果两个平行平面同时和第三个平面相交,那么它们的交线平行. 上述定理通常称为平面与平面平行的性质定理,该定理用符号语言可怎样表述?a//b想一想:平面与平面平行的性质定理可简述为“面面平行,则线线平行”,在实际应用中它有何功能作用?功能作用:可以由平面与平面平行得出直线与直线平行.平面和平面平行的判定定理:直线与直线平行平面与平面平行平面和平面平行的性质定理结论:1、若两个平面互相平行,则其中一个平面中的直线必平行于另一个平面;
2、平行于同一平面的两平面平行;
3、过平面外一点有且只有一个平面与这个平面平行;
4、夹在两平行平面间的平行线段相等.例1.?求证:夹在两个平行平面间的平行线段相等.如图,α//β,AB//CD,且A∈α,
C∈α,B∈β,D∈β.
求证:AB=CD.证明 因为AB//CD,所以过AB,CD可作平面γ,且平面γ与平面α和β分别相交于AC和BD.因为α//β,所以BD//AC.因此,四边形ABDC是平行四边形.所以AB=CD.例2 如图,平面α,β,γ两两平行,且直线l与α,β,γ分别交于点A,B,C,直线m与α,β,γ分别交于点D,E,F,AB=6,BC=2,EF=3.求DE的长.解 当直线m与l共面时,该平面与α,β,γ分别交于直线AD,BE,CF,因为α,β,γ两两平行,所以AD∥BE
∥CF,故当直线m与l不共面时,连接DC.
设DC与β相交于点G,则平面ACD与α,β分别相交于直线AD,BG,平面DCF与β,γ分别交于直线GE,CF.因为α,β,γ两两平行,所以BG∥ AD,GE∥CF.
因此所以 又因为AB=6,BC=2,EF=3,所以,DE=9.1、设平面α∥平面β,A∈α,B∈β,C是AB的中点,当
A、B分别在α、β内运动时,那么所有的动点C( )A.不共面;
B.当且仅当A、B在两条相交直线上移动时才共面;
C.当且仅当A、B在两条给定的平行直线上移动时才共面;
D.不论A、B如何移动都共面.D2.过长方体ABCD-A1B1C1D1的任意两条棱的中点作直线,
其中能够与平面ACC1A1平行的直线有________条.【解析】如图,与AC平行的直线有4条,与AA1平行的直线有4条,连接MN,则MN∥面ACC1A1,这样的直线也有4条(包括MN).123.正方体ABCD-A1B1C1D1中,E、M、F为棱B1C1,C1D1和B1B的中点,试过E、M作一平面与平面A1FC平行.解 如图,取CC1中点G,连接B1G,取C1G中点H,连接EH.则EH∥B1G∥FC.
同理,连接MH.则MH∥A1F.
连接EM,
又MH∩EH=H,
∴面EMH∥面A1FC,
即面EHM为所求平面. 如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.面面平行的判定定理面面平行的性质定理 如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
