1.5.2 直线与平面平行的性质 课件3
文档属性
| 名称 | 1.5.2 直线与平面平行的性质 课件3 |

|
|
| 格式 | zip | ||
| 文件大小 | 767.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-22 00:00:00 | ||
图片预览




文档简介
课件20张PPT。1.5.2 直线与平面平行的性质1、使学生掌握直线与平面平行的性质,并会应用性质解决问题;
2、理解直线与平面的位置关系要转化为直线与直线的位置关系的转化思想;
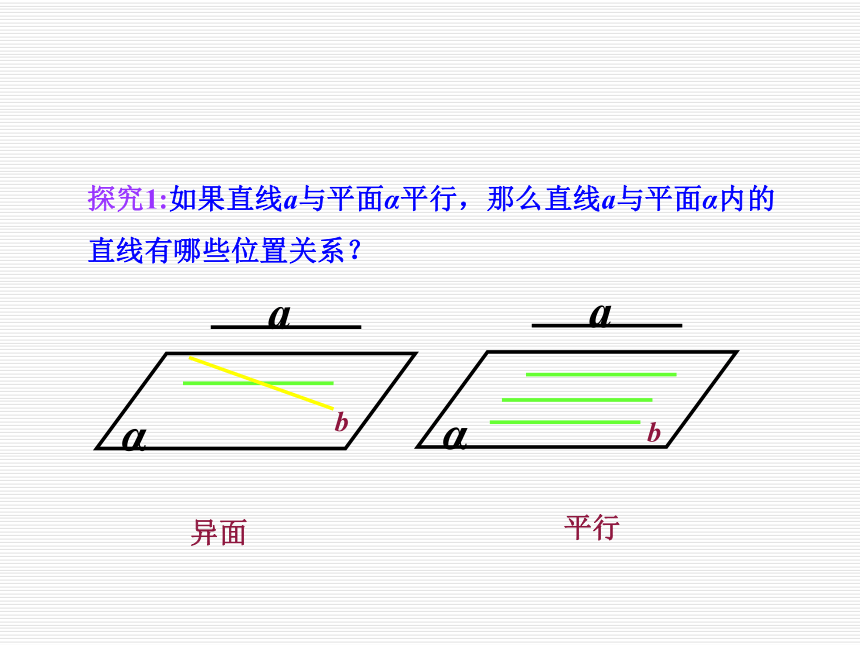
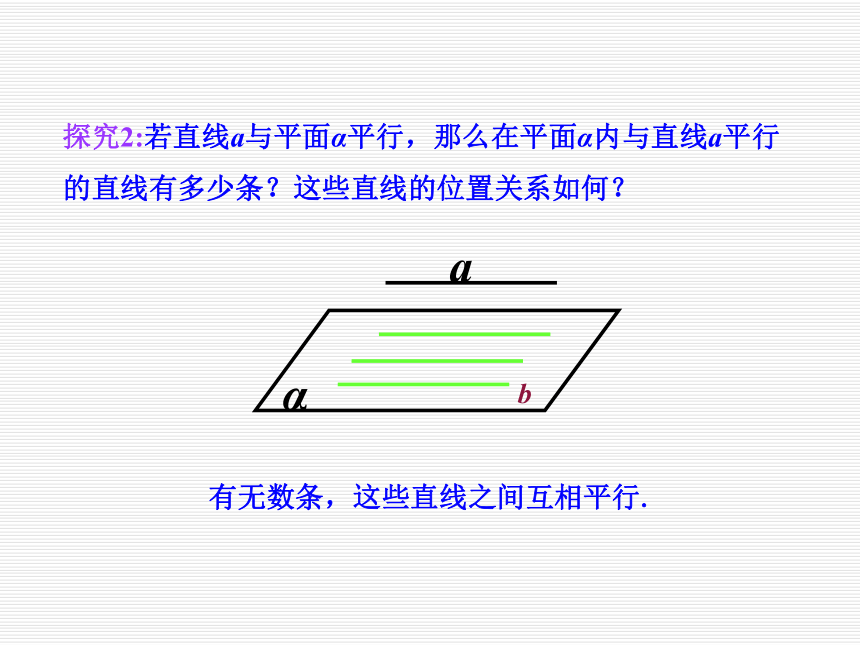
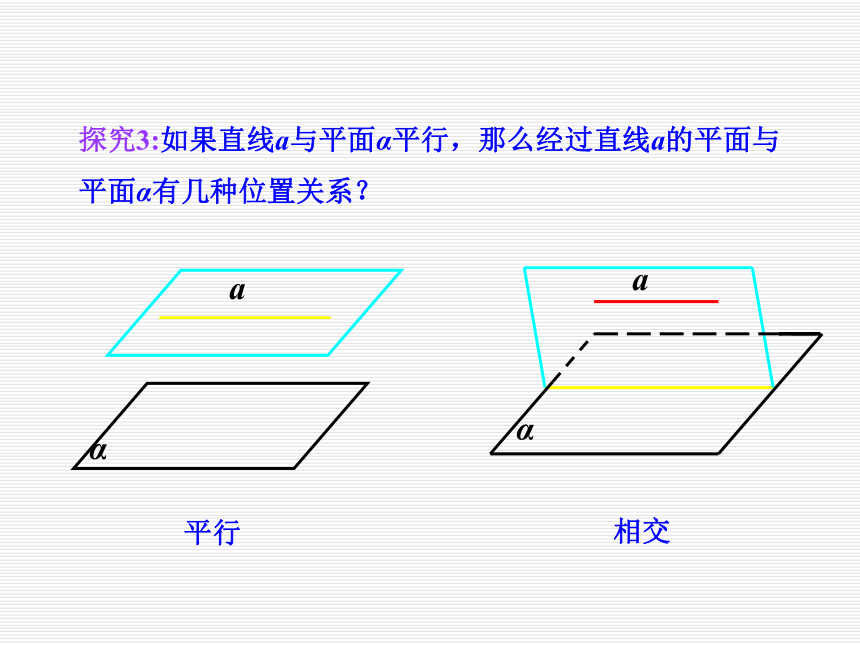
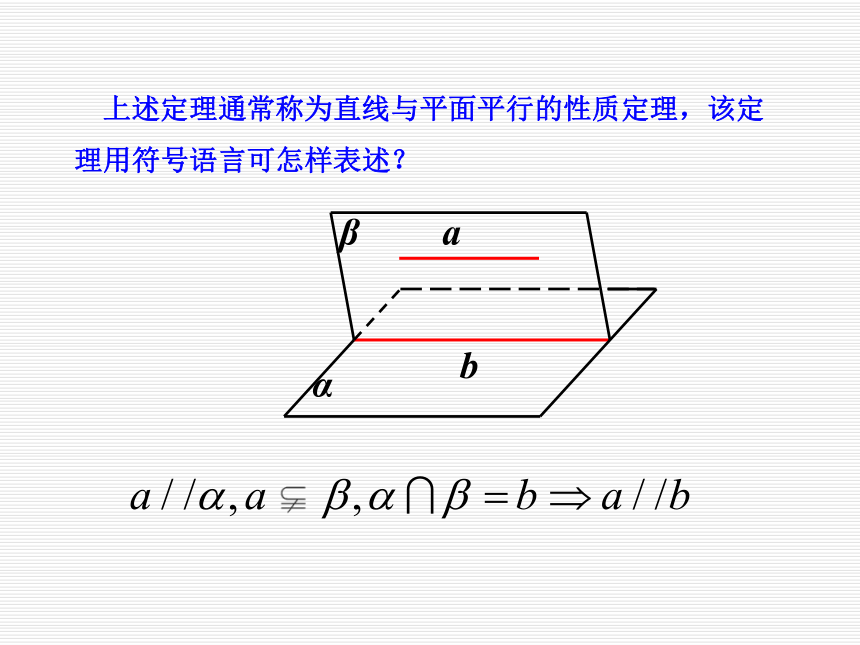
3、让学生在发现中学习,增强学习的积极性;让学生了解空间与平面互相转换的数学思想. 前面我们知道了如何来判断直线与平面平行,那么,已知直线和平面平行,我们又能有怎样的结论呢?探究1:如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?异面平行探究2:若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?有无数条,这些直线之间互相平行.探究3:如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?平行相交探究4:如果直线a与平面α平行,经过直线a的平面与平面α相交于直线b,那么直线a、b的位置关系如何?为什么?平行.
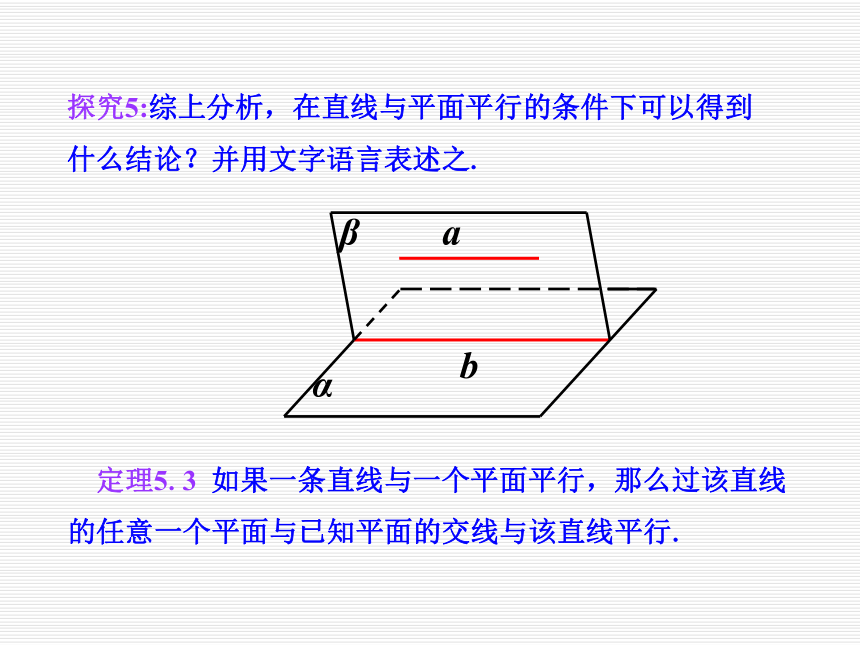
因为a∥α,所以a 和α没有公共点.
又因为b在α 内,所以b和α也没有公共点.
而a和b都在平面β内,又没有公共点,所以a∥b.探究5:综上分析,在直线与平面平行的条件下可以得到什么结论?并用文字语言表述之. 定理5.3 如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行. 上述定理通常称为直线与平面平行的性质定理,该定理用符号语言可怎样表述? 直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?提供了作平行线的方法,并且是判断线线平行的依据. 直线和平面平行的判定定理:直线与直线平行直线与平面平行直线和平面平行的性质定理.注意: 平面外的一条直线只要和平面内的任一条直线平行,则就可以得到这条直线和这个平面平行;但是若一条直线与一个平面平行,则这条直线并不是和平面内的任一条直线平行,它只与该平面内与它共面的直线平行.例1 如图A,B,C,D在同一平面内,AB∥平面α,AC∥BD,且AC,BD与α分别交于点C,D求证:AC=BD.证明 连接CD.
因为A,B,C,D在同一平面内,
AB∥平面α,所以AB∥CD.
又因为AC∥BD,所以四边形ABCD是平行四边形
因此 AC=BD.α例2 如下图,已知四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.
求证:AP∥GH.解 如右图,连结AC,设AC交BD于O,连结MO.又经过PA与点G的平面交平面BDM于GH,
∴AP∥GH.又∵MO 平面BDM,PA 平面BDM,
∴PA∥平面BDM.∵四边形ABCD是平行四边形,
∴O是AC的中点.
又∵M是PC的中点,∴MO∥PA.1、教室内的日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行? 答:只需由灯管两端向地面引两条平行线,过两条平行线与地面的交点的连线就是与灯管平行的直线.2.已知直线a、b和平面α、β,则在下列命题中,真
命题为( )
A.若a∥β,α∥β,则a∥α
B.若α∥β,a α,则a∥β
C.若α∥β,a α,b β,则a∥b
D.若a∥β,b∥α,α∥β,则a∥bB【解析】A中a可能在α内,C中a、b可能异面,D中a、b
可能异面,B中α∥β,a α,则a与β无公共点,∴a∥β.3.已知α∥β,a α,B∈β,则在β内过点B的所有直
线中( )
A.不一定存在与a平行的直线
B.只有两条与a平行的直线
C.存在无数条与a平行的直线
D.存在唯一一条与a平行的直线D【解析】因为a与B确定一个平面,该平面与β的交线即为符合条件的直线.C【解析】A中n与α可能相交,B中n与α可能平行,D中m、n可能相交,C中m即m、n所在平面与α的交线.4.对于直线m,n和平面α,下面命题中的真命题是( )
A.如果m?α,n α,m,n是异面直线,那么n∥α
B.如果m?α,n α,m,n是异面直线,那么n与α相交
C.如果m?α,n∥α,m,n共面,那么m∥n
D.如果m∥α,n∥α,m,n共面,那么m∥n5、如图,已知直线a,b,平面α,且a//b,a//α,a,b都在平面α外.求证:b//α.证明 过a作平面β,使它与平面α相交,交线为c.因为a//b,所以,b//c.
又因为c?α,?b??α,
所以?b//?α.因为a//α,a?β,α∩β=c,所以?a//?c.? 如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.线线平行 线面平行线面平行的判定定理线面平行的性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
2、理解直线与平面的位置关系要转化为直线与直线的位置关系的转化思想;
3、让学生在发现中学习,增强学习的积极性;让学生了解空间与平面互相转换的数学思想. 前面我们知道了如何来判断直线与平面平行,那么,已知直线和平面平行,我们又能有怎样的结论呢?探究1:如果直线a与平面α平行,那么直线a与平面α内的直线有哪些位置关系?异面平行探究2:若直线a与平面α平行,那么在平面α内与直线a平行的直线有多少条?这些直线的位置关系如何?有无数条,这些直线之间互相平行.探究3:如果直线a与平面α平行,那么经过直线a的平面与平面α有几种位置关系?平行相交探究4:如果直线a与平面α平行,经过直线a的平面与平面α相交于直线b,那么直线a、b的位置关系如何?为什么?平行.
因为a∥α,所以a 和α没有公共点.
又因为b在α 内,所以b和α也没有公共点.
而a和b都在平面β内,又没有公共点,所以a∥b.探究5:综上分析,在直线与平面平行的条件下可以得到什么结论?并用文字语言表述之. 定理5.3 如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行. 上述定理通常称为直线与平面平行的性质定理,该定理用符号语言可怎样表述? 直线与平面平行的性质定理可简述为“线面平行,则线线平行”,在实际应用中它有何功能作用?提供了作平行线的方法,并且是判断线线平行的依据. 直线和平面平行的判定定理:直线与直线平行直线与平面平行直线和平面平行的性质定理.注意: 平面外的一条直线只要和平面内的任一条直线平行,则就可以得到这条直线和这个平面平行;但是若一条直线与一个平面平行,则这条直线并不是和平面内的任一条直线平行,它只与该平面内与它共面的直线平行.例1 如图A,B,C,D在同一平面内,AB∥平面α,AC∥BD,且AC,BD与α分别交于点C,D求证:AC=BD.证明 连接CD.
因为A,B,C,D在同一平面内,
AB∥平面α,所以AB∥CD.
又因为AC∥BD,所以四边形ABCD是平行四边形
因此 AC=BD.α例2 如下图,已知四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.
求证:AP∥GH.解 如右图,连结AC,设AC交BD于O,连结MO.又经过PA与点G的平面交平面BDM于GH,
∴AP∥GH.又∵MO 平面BDM,PA 平面BDM,
∴PA∥平面BDM.∵四边形ABCD是平行四边形,
∴O是AC的中点.
又∵M是PC的中点,∴MO∥PA.1、教室内的日光灯管所在的直线与地面平行,如何在地面上作一条直线与灯管所在的直线平行? 答:只需由灯管两端向地面引两条平行线,过两条平行线与地面的交点的连线就是与灯管平行的直线.2.已知直线a、b和平面α、β,则在下列命题中,真
命题为( )
A.若a∥β,α∥β,则a∥α
B.若α∥β,a α,则a∥β
C.若α∥β,a α,b β,则a∥b
D.若a∥β,b∥α,α∥β,则a∥bB【解析】A中a可能在α内,C中a、b可能异面,D中a、b
可能异面,B中α∥β,a α,则a与β无公共点,∴a∥β.3.已知α∥β,a α,B∈β,则在β内过点B的所有直
线中( )
A.不一定存在与a平行的直线
B.只有两条与a平行的直线
C.存在无数条与a平行的直线
D.存在唯一一条与a平行的直线D【解析】因为a与B确定一个平面,该平面与β的交线即为符合条件的直线.C【解析】A中n与α可能相交,B中n与α可能平行,D中m、n可能相交,C中m即m、n所在平面与α的交线.4.对于直线m,n和平面α,下面命题中的真命题是( )
A.如果m?α,n α,m,n是异面直线,那么n∥α
B.如果m?α,n α,m,n是异面直线,那么n与α相交
C.如果m?α,n∥α,m,n共面,那么m∥n
D.如果m∥α,n∥α,m,n共面,那么m∥n5、如图,已知直线a,b,平面α,且a//b,a//α,a,b都在平面α外.求证:b//α.证明 过a作平面β,使它与平面α相交,交线为c.因为a//b,所以,b//c.
又因为c?α,?b??α,
所以?b//?α.因为a//α,a?β,α∩β=c,所以?a//?c.? 如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.线线平行 线面平行线面平行的判定定理线面平行的性质定理 如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.
