1.6.2 直线与平面垂直的性质 课件1
文档属性
| 名称 | 1.6.2 直线与平面垂直的性质 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 775.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-22 00:00:00 | ||
图片预览










文档简介
课件72张PPT。1.6.2 直线与平面垂直的性质1.平面内证明线线平行的方法
(1)两条直线被第三条直线所截,若同位角相等(或内错角相等或同旁内角互补),则两直线平行.
(2)三角形中位线、梯形中位线的性质.
(3)平行四边形对边平行的性质.
(4)平行线分线段成比例定理.线面垂直性质定理的应用 2.空间中证明线线平行的方法
(1)平行于同一条直线的两条直线互相平行.
(2)线面平行的性质定理:如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行.
(3)面面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
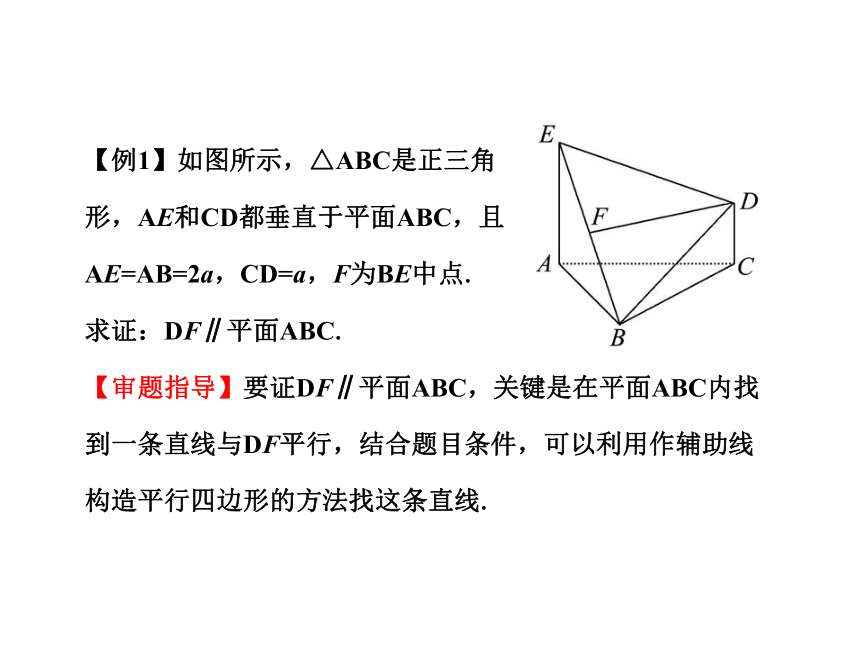
(4)线面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.【例1】如图所示,△ABC是正三角
形,AE和CD都垂直于平面ABC,且
AE=AB=2a,CD=a,F为BE中点.
求证:DF∥平面ABC.
【审题指导】要证DF∥平面ABC,关键是在平面ABC内找到一条直线与DF平行,结合题目条件,可以利用作辅助线构造平行四边形的方法找这条直线.【规范解答】取AB的中点G,连接FG、GC.
∵F为BE的中点,
∴FG∥AE且
而AE⊥平面ABC,
∴FG⊥平面ABC.
又∵CD⊥平面ABC,
∴FG∥CD且FG=CD=a.
∴四边形CDFG为平行四边形.
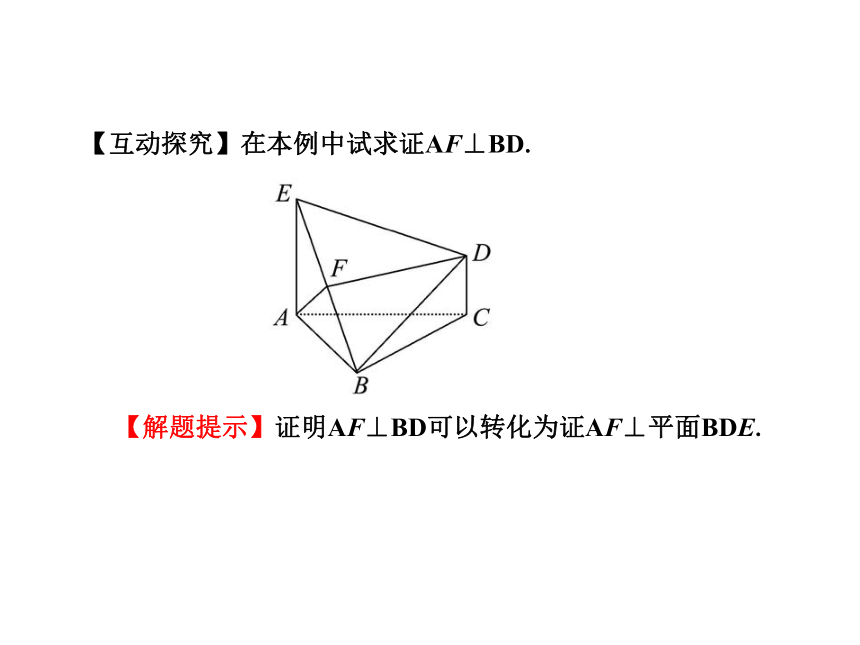
于是DF∥CG. 故DF∥平面ABC.【互动探究】在本例中试求证AF⊥BD.
【解题提示】证明AF⊥BD可以转化为证AF⊥平面BDE.【证明】取AB的中点G,连接FG、GC.
∵AE⊥平面ABC,CG 平面ABC,∴CG⊥AE.
又∵△ABC是正三角形,且G为AB的中点,
∴CG⊥AB.
又∵AE∩AB=A,∴CG⊥平面ABE.又∵AF 平面ABE,∴AF⊥CG.
由例题知DF∥CG. ∴AF⊥DF.
而EA=AB, F为BE中点.
∴AF⊥BE. 又BE∩DF=F,
∴AF⊥平面BDE ,∴AF⊥BD. 空间中证明线线垂直的方法
(1)共面直线垂直的证明方法:
①利用等腰三角形“三线合一”的性质证明.即等腰三角形底边上的中线(或顶角平分线)是底边上的高.
②利用矩形的四个角是直角证明.
③利用菱形的对角线互相垂直平分证明.
④利用直径所对的圆周角是直角证明.
⑤利用勾股定理的逆定理证明.由线面垂直证明线线垂直(2)异面直线垂直的证明方法:
①作异面直线所成的角,并计算其为90°.
②转化为证明线面垂直.也就是说,要证明线线垂直只要证明其中一条直线垂直于经过另外一条直线的平面即可.其证明过程通常如下: 在几何体的直观图中,互相垂直的两条直线,看上去可能已经不垂直,因此解题时一方面要注重逻辑推理,另一方面要注重转化思想的应用.【例2】 (2010·湖北高考改编)如图,
在四面体ABOC中,OC⊥OA,OC⊥OB,
∠AOB=120°,且OA=OB=OC=1.设P为AC
的中点,Q在AB上且AB=3AQ,
证明:PQ⊥OA.
【审题指导】要证PQ⊥OA可以有两种思路:一是证明PQ垂直于过OA的平面;二是证明OA垂直于过PQ的平面.本题中两种方法都不容易实现,可以转化为证明其中一条直线和另外一条直线的平行线垂直.【规范解答】在平面OAB内过O点作
ON⊥OA交AB于N,连接NC.
在等腰△AOB中,∠AOB=120°,
∴∠OAB=∠OBA=30°,
在Rt△AON中,∠OAN=30°,
在△ONB中∠NOB=120°-90°=30°=∠NBO,又∵AB=3AQ,∴Q为AN的中点.在△CAN中,
∵P,Q分别为AC,AN的中点,∴CN∥PQ.
由ON⊥OA,OC⊥OA知OA⊥平面ONC,
又∵NC 平面ONC,∴OA⊥NC,
由CN∥PQ知PQ⊥OA.【变式训练】如图,
在底面为平行四边形的四棱锥P-ABCD
中,AB⊥AC,PA⊥平面ABCD,点E是
PD的中点.
(1)求证:AC⊥PB.
(2)求证:PB∥平面AEC. 【解题提示】(1)要证AC⊥PB,只需证AC⊥平面PAB.
(2)要证PB∥平面AEC,只要利用平行四边形的性质,连接BD与AC相交,就可以在△PBD中证明线线平行,进而证明线面平行.【证明】(1)∵PA⊥平面ABCD,AC 平面ABCD,
∴PA⊥AC.
又∵AB⊥AC,PA∩AB=A,PA 平面PAB,
AB 平面PAB,∴AC⊥平面PAB,∴AC⊥PB.(2)连接BD交AC于点O,并连接EO.
∵四边形ABCD为平行四边形.
∴O为BD的中点.又∵E为PD的中点,
∴在△PDB中EO为中位线,EO∥PB.
∵PB 平面AEC,EO 平面AEC,
∴PB∥平面AEC .【例】如图所示,四边形ABCD为正方形,
SA⊥平面ABCD,过点A且垂直于SC的平面
分别交SB、SC、SD于点E、F、G.
求证:AE⊥SB.
【审题指导】证明本题的关键是要分析出由SA⊥平面ABCD及ABCD是正方形可证BC⊥平面SAB.【规范解答】∵SA⊥平面ABCD,BC? 平面ABCD,
∴SA⊥BC.
又∵BC⊥AB,SA∩AB=A,∴BC⊥平面SAB,
又∵AE 平面SAB,∴BC⊥AE.
∵SC⊥平面AEFG,AE 平面AEFG,∴SC⊥AE.
又∵BC∩SC=C,∴AE⊥平面SBC,
∴AE⊥SB.【变式备选】如图,已知矩形ABCD,
过点A作SA⊥平面ABC,再过点A作AE
⊥SB于点E,过点E作EF⊥SC于点F.
(1)求证:AF⊥SC;
(2)若平面AEF交SD于点G,求证:AG⊥SD.【证明】(1)∵SA⊥平面ABC,BC 平面ABC,
∴SA⊥BC.
∵四边形ABCD是矩形,∴AB⊥BC.
∵AB∩SA=A,∴BC⊥平面SAB.
∵AE 平面SAB,∴BC⊥AE.∵SB⊥AE,BC∩SB=B,
∴AE⊥平面SBC,∴AE⊥SC.
∵EF⊥SC,AE∩EF=E,
∴SC⊥平面AEF.
∵AF 平面AEF,∴AF⊥SC.(2)∵SA⊥平面ABC,DC 平面ABC,∴SA⊥DC.
∵四边形ABCD为矩形,
∵AD⊥DC,SA∩AD=A,∴DC⊥平面SAD.
∵AG 平面SAD,∴DC⊥AG.
由(1)可知SC⊥平面AEF,AG 平面AEF,
∴SC⊥AG.
∵SC∩DC=C,∴AG⊥平面SDC.
∵SD 平面SCD,∴SD⊥AG.1.直线与平面垂直的性质
(1)证明线线平行:若l⊥α,m⊥α,则l∥m.
(2)证明线线垂直:若l⊥α,m α,则l⊥m.
(3)证明面面平行:若l⊥α,l⊥β,则α∥β.
(4)证明线面垂直:①若l∥m,l⊥α,则m⊥α.
②若l⊥α,α∥β,则l⊥β.线面垂直性质的综合应用2.线面垂直与平行的相互转化
(1)空间中直线与直线垂直,直线与平面垂直,直线与平面平行,直线与直线平行可以相互转化,每一种垂直与平行的判定都是从某种垂直与平行开始转化为另一种垂直与平行,最终达到目的.
(2)转化关系
“平行关系”与“垂直关系”在特定条件下是可以相互转化的.【例3】如图,在
多面体ABCDEF中,四边形ABCD是正
方形,AB=2EF=2,EF∥AB,EF⊥FB,
∠BFC=90°,BF=FC,H为BC的中点,
(1)求证:FH∥平面EDB;
(2)求证:AC⊥平面EDB;
【审题指导】(1)可以根据EF∥AB作辅助线,在平面EDB中作直线与FH平行,(2)在(1)的基础上利用EF⊥FB,可以先推出EF⊥平面BFC,由此进一步思考如何证明AC⊥平面EDB.【规范解答】(1)连接AC与BD交于点G,则G为AC的中点,连
接EG、GH,由于H为BC的中点,故GH AB.
又∵EF AB,∴GH EF,
∴四边形EFHG为平行四边形.
∴EG∥FH,而EG 平面EDB,FH 平面EDB.
∴FH∥平面EDB.(2)由四边形ABCD为正方形知AB⊥BC,
又∵EF∥AB,∴EF⊥BC,而EF⊥FB,且BC∩FB=B,
∴EF⊥平面BFC,∴EF⊥FH,∴AB⊥FH.
∵BF=FC,H为BC的中点,
∴FH⊥BC,且BC∩AB=B,
∴FH⊥平面ABCD,∴FH⊥AC.
又∵FH∥EG,∴AC⊥EG.
又∵AC⊥BD,且EG∩BD=G,∴AC⊥平面EDB.【变式训练】如图所示的几何体是将高为
2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半
沿切面向右水平平移后得到的.A,A′,B,B′分别为CD,
的中点,O1,O1′,O2,O2′分别为CD,
C′D′,DE,D′E′的中点.(1)证明:O1′,A′,O2,B四点共面;
(2)设G为AA′中点,延长A′O1′到H′,使得O1′H′= A′O1′.
证明:BO2′⊥平面H′B′G′.【证明】(1)由已知得,O1′A′∥O2′B′,O2′B′∥O2B.
得O1′A′∥O2B,所以O1′A′与O2B确定一个平面α,且O1′,A′,O2,B都在平面α内,即O1′,A′,O2,B四点共面.(2)如图,延长AO1到I使AO1=O1I,连接IH′及IO1′,由已知可得H′B′⊥平面A′AIH′,从而H′B′⊥IO1′,又在矩形A′AIH ′中O1′、G分别为边A′H′与AA′的中点,所以IO1′⊥H′G,所以IO1′⊥平面H′B′G.
连接IB,则IBO2′O1′
为矩形,所以BO2′∥
IO1′,所以BO2′⊥平
面H′B′G.【典例】(12分)图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的主视图和左视图如图2所示.
(1)证明:AD⊥平面PBC;
(2)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.【审题指导】(1)由主视图和左视图可知PA=AC=4,D为PC的中点,进一步可得AD⊥PC.另一方面可通过证BC⊥平面PAC,得BC⊥AD;(2)将问题转化到直角三角形中,利用勾股定理求解.【规范解答】(1)因为PA⊥平面ABC,所以PA⊥BC,
又∵AC⊥BC,PA∩AC=A,∴BC⊥平面PAC,
……………………………………………………………2分∴BC⊥AD. ………………………………………………3分
由三视图可得,在△PAC中,PA=AC=4,
D为PC的中点,∴AD⊥PC,∵BC∩PC=C. ……………4分
∴AD⊥平面PBC. ………………………………………5分(2)取AB的中点O,连接CO并延长至Q,
使得CQ=2OC,点Q即为所求. …………………………6分
∵O为CQ的中点,连接PQ,OD,∴PQ∥OD,
∵PQ? 平面ABD,OD 平面ABD,
∴PQ∥平面ABD,………………………………………8分连接AQ,BQ,因为四边形ACBQ的对角线互相平分,
∴四边形ACBQ为平行四边形,所以AQ=4,
……………………………………………………………10分
又PA⊥平面ABC,AQ 平面ABC,∴PA⊥AQ,
∴在Rt△PAQ中,
…………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】四棱锥P-ABCD的三视图如图,四边形ABCD为正方形,E是侧棱PC上的动点,试问不论点E在何位置,是否都有BD⊥AE?证明你的结论.【解析】不论点E在何位置,都有BD⊥AE.
证明如下:连接AC.
∵四边形ABCD是正方形,∴BD⊥AC.
∵PC⊥底面ABCD且BD 平面ABCD,∴BD⊥PC.
又∵AC∩PC=C,∴BD⊥平面PAC.
∵不论点E在何位置,AE 平面PAC总成立,
∴都有BD⊥AE.1.正方体ABCD-A1B1C1D1中,E为A1C1的中点,则直线CE垂直于( )
(A)AC (B)BD
(C)A1D1 (D)A1A
【解析】选B.因为BD⊥平面AA1C1C,CE 平面AA1C1C,所以CE⊥BD.2.若a,b表示直线,α表示平面,下列说法正确的序号是__________.
①若a⊥α,b∥α,则a⊥b; ②若a⊥α,a⊥b,则b∥α;
③若a∥α,a⊥b,则b⊥α.
【解析】由线面垂直的性质知①正确.②中b可能满足
B α,故②错误;③中b可能与α相交(不垂直),也可能
与α平行,故③错误.
答案:①3.在Rt△ABC中,D是斜边AB的中点,AC=6,BC=8,EC⊥平面ABC,且EC=12,则ED=__________.
【解析】∵EC⊥平面ABC,∴EC⊥CD.
∵在Rt△ABC中, AC=6,BC=8,∴AB=10.
又∵D是斜边AB的中点,
∴在Rt△ECD中,
答案:134.地面上有两根旗杆,底端相距a米,它们的高分别是b米和c米(b>c),则它们顶端的距离为___________.
【解析】如图,由于两旗杆都与地面垂
直,故两旗杆AD与BC平行,且四边形
ABCD是直角梯形,AD=c,BC=b,过D作
DE⊥BC于E,则DE=a,CE=b-c,
答案: 5.在长方体ABCD-A1B1C1D1中,E∈平面ABCD,F∈平面A1B1C1D1,
且EF⊥平面ABCD,求证A1F AE.【证明】如图所示,由长方体的性质可知,AA1⊥平面ABCD.
又∵EF⊥平面ABCD,
∴EF∥AA1,故EF与AA1确定一个平面AEFA1.
∵平面AEFA1∩平面A1B1C1D1=A1F,
平面AEFA1∩平面ABCD=AE.
平面ABCD∥平面A1B1C1D1,∴A1F∥AE,
∴四边形AEFA1为平行四边形,
∴A1F AE.一、选择题(每题4分,共16分)
1.已知α,β是平面,m,n是直线,则下列说法中不正确的是( )
(A)若m∥n,m⊥α,则n⊥α
(B)若m∥α,α∩β=n,则m∥n
(C)若m⊥α,m⊥β,则α∥β
(D)若m⊥α,m β,则α⊥β【解析】选B.A正确,若m∥n,m⊥α,则n与平面α内的任意一条直线垂直,故n⊥α.B错误, 应该是当m∥α,α∩β=n,且m β时,m∥n. C正确,如图所示,过m作平面γ和平面δ,可证γ与α、β的交线都与m垂直,又都在同一平面内,故平行.同理δ与α、β的交线也互相平行,所以α∥β.D正确.2. 点A、B在平面α的同侧,点C
是线段AB的中点,过A、B、C三点
分别作AA1,BB1,CC1与平面α垂直,
垂足分别为A1,B1,C1,若AA1=3,
CC1=5,则BB1=( )
(A)1 (B)7
(C)1或7 (D)8【解析】选B.∵AA1⊥α,BB1⊥α,CC1⊥α,
∴AA1∥BB1∥CC1.
又AA1=3,CC1=5,
∴CC1是梯形AA1B1B的中位线,
∴BB1=2CC1-AA1=2×5-3=7.3.如图,△ABC中,∠ACB=90°,直线l
过点A且垂直于平面ABC,动点P∈l,
当点P逐渐远离点A时,∠PCB的大小
( )
(A)变大 (B)变小
(C)不变 (D)有时变大有时变小【解析】选C.∵l⊥平面ABC,∴BC⊥l.
∵∠ACB=90°,∴BC⊥AC.
又l∩AC=A,∴BC⊥平面PAC,
∴BC⊥PC,∴∠PCB=90°.4.如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BC,DD1上的点,如果B1E⊥平面ABF,则E、F满足的条件一定是
( )
(B)CE+DF=1
(C)CE+D1F=1
(D)E、F在棱BC、DD1上的任意位置【解析】选B.在平面BB1C1C内作BF′∥AF交CC1于点F′.
∵B1E⊥平面ABF,∴B1E⊥AF,
∴B1E⊥BF′,DF=CF′.
在正方形BB1C1C中,
由B1E⊥BF′得CE=C1F′=1-CF′,
∴CE+CF′=1,即CE+DF=1.二、填空题(每题4分,共8分)
5.如图,AB
是⊙O的直径,C是圆周上不同于A、
B的点,PA垂直于⊙O所在的平面,
AE⊥PB于E,AF⊥PC于F.因此
__________⊥平面PBC.(请填图上
的一条直线)【解析】∵PA垂直于⊙O所在的平面,BC在⊙O所在的平面内,∴PA⊥BC.
∵C是圆周上不同于A、B的点,∴BC⊥AC.
又PA∩AC=A,∴BC⊥平面PAC.
又AF 平面PAC,∴BC⊥AF.
∵AF⊥PC且BC∩PC=C,∴AF⊥平面PBC.
答案:AF6.如图,PA⊥平面ABC,∠ACB=90°,EF∥PA,则图中直角三角形的个数是__________.【解析】由PA⊥平面ABC,得PA⊥AB,PA⊥AC,PA⊥BC.
又∵BC⊥AC,AC∩PA=A,∴BC⊥平面PAC,∴BC⊥PC.
∵EF∥PA,PA⊥平面ABC,∴EF⊥平面ABC,∴EF⊥BE,EF⊥EC,
∴△PAB、△PAC、△ABC、△PBC、△EFC、△BEF均为直角三角形.
答案:6
【易错提醒】△PBC是直角三角形容易漏掉,原因是未分析出BC⊥平面PAC这一条件.三、解答题(每题8分,共16分)
7.如图,在直三棱柱ABC-A1B1C1中,
AC=9,BC=12,AB=15,AA1=12.
求证:AC⊥B1C.
【解题提示】要证明AC⊥B1C,根据题目条件只要证明
AC⊥平面BB1C1C.【证明】∵AC=9,BC=12,AB=15,
∴AB2=AC2+BC2,∴∠ACB=90°,AC ⊥BC.
∵CC1⊥平面ABC,AC 平面ABC.
∴AC⊥CC1,又CC1∩BC=C,
∴AC⊥平面BB1C1C .
∵B1C 平面BB1C1C, ∴AC⊥B1C.8.如图所示,在正方体ABCD-A1B1C1D1中,
M是AB上一点,N是A1C的中点,
MN⊥平面A1DC.
求证:(1)MN∥AD1;
(2)M是AB的中点.【证明】(1)∵ADD1A1为正方形,∴AD1⊥A1D.
又∵CD⊥平面ADD1A1,AD1 平面ADD1A1,
∴CD⊥AD1.
∵A1D∩CD=D,
∴AD1⊥平面A1DC.
又∵MN⊥平面A1DC,
∴MN∥AD1.(2)连接ON,在△A1DC中,
A1O=OD,A1N=NC.
∴ON CD AB,
∴ON∥AM.
又∵MN∥OA,∴四边形AMNO为平行四边形,
∴ON=AM.
∴M是AB的中点. 【方法技巧】解读线面垂直的性质的应用
学习线面垂直的性质的意义在于建立“平行关系”与“垂直关系”的相互转化意识.因此通过性质的学习,可以让我们对空间点、线、面的位置关系有一个更为全面、系统的认识.
在应用线面垂直的性质时,要注意尽量多地分析出题目条件中所隐含的线面垂直、线线平行、面面平行等位置关系,同时要根据题目所证结论设计证明思路.【挑战能力】
(10分)已知AA1⊥平面ABC,
AB=BC=AA1=CA,P为A1B上的点.
(1)当P为A1B中点时,求证:
AB⊥PC;
(2)当二面角P-AC-B的大小为60°时,
求 的值.【解析】(1)当 时,作PD∥AA1交AB于D,
连接CD.
由AA1⊥平面ABC,
知PD⊥平面ABC.
当P为A1B中点时,D为AB中点.
∵△ABC为正三角形,
∴CD⊥AB,∴AB⊥平面PCD,∴PC⊥AB.(2)过D作DE⊥AC于E,连接PE,则PE⊥AC,
∴∠DEP为二面角P-AC-B的平面角,即
∵PD∥A1A,AA1=AB,∴PD=BD,AA1=AB,
(1)两条直线被第三条直线所截,若同位角相等(或内错角相等或同旁内角互补),则两直线平行.
(2)三角形中位线、梯形中位线的性质.
(3)平行四边形对边平行的性质.
(4)平行线分线段成比例定理.线面垂直性质定理的应用 2.空间中证明线线平行的方法
(1)平行于同一条直线的两条直线互相平行.
(2)线面平行的性质定理:如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行.
(3)面面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.
(4)线面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.【例1】如图所示,△ABC是正三角
形,AE和CD都垂直于平面ABC,且
AE=AB=2a,CD=a,F为BE中点.
求证:DF∥平面ABC.
【审题指导】要证DF∥平面ABC,关键是在平面ABC内找到一条直线与DF平行,结合题目条件,可以利用作辅助线构造平行四边形的方法找这条直线.【规范解答】取AB的中点G,连接FG、GC.
∵F为BE的中点,
∴FG∥AE且
而AE⊥平面ABC,
∴FG⊥平面ABC.
又∵CD⊥平面ABC,
∴FG∥CD且FG=CD=a.
∴四边形CDFG为平行四边形.
于是DF∥CG. 故DF∥平面ABC.【互动探究】在本例中试求证AF⊥BD.
【解题提示】证明AF⊥BD可以转化为证AF⊥平面BDE.【证明】取AB的中点G,连接FG、GC.
∵AE⊥平面ABC,CG 平面ABC,∴CG⊥AE.
又∵△ABC是正三角形,且G为AB的中点,
∴CG⊥AB.
又∵AE∩AB=A,∴CG⊥平面ABE.又∵AF 平面ABE,∴AF⊥CG.
由例题知DF∥CG. ∴AF⊥DF.
而EA=AB, F为BE中点.
∴AF⊥BE. 又BE∩DF=F,
∴AF⊥平面BDE ,∴AF⊥BD. 空间中证明线线垂直的方法
(1)共面直线垂直的证明方法:
①利用等腰三角形“三线合一”的性质证明.即等腰三角形底边上的中线(或顶角平分线)是底边上的高.
②利用矩形的四个角是直角证明.
③利用菱形的对角线互相垂直平分证明.
④利用直径所对的圆周角是直角证明.
⑤利用勾股定理的逆定理证明.由线面垂直证明线线垂直(2)异面直线垂直的证明方法:
①作异面直线所成的角,并计算其为90°.
②转化为证明线面垂直.也就是说,要证明线线垂直只要证明其中一条直线垂直于经过另外一条直线的平面即可.其证明过程通常如下: 在几何体的直观图中,互相垂直的两条直线,看上去可能已经不垂直,因此解题时一方面要注重逻辑推理,另一方面要注重转化思想的应用.【例2】 (2010·湖北高考改编)如图,
在四面体ABOC中,OC⊥OA,OC⊥OB,
∠AOB=120°,且OA=OB=OC=1.设P为AC
的中点,Q在AB上且AB=3AQ,
证明:PQ⊥OA.
【审题指导】要证PQ⊥OA可以有两种思路:一是证明PQ垂直于过OA的平面;二是证明OA垂直于过PQ的平面.本题中两种方法都不容易实现,可以转化为证明其中一条直线和另外一条直线的平行线垂直.【规范解答】在平面OAB内过O点作
ON⊥OA交AB于N,连接NC.
在等腰△AOB中,∠AOB=120°,
∴∠OAB=∠OBA=30°,
在Rt△AON中,∠OAN=30°,
在△ONB中∠NOB=120°-90°=30°=∠NBO,又∵AB=3AQ,∴Q为AN的中点.在△CAN中,
∵P,Q分别为AC,AN的中点,∴CN∥PQ.
由ON⊥OA,OC⊥OA知OA⊥平面ONC,
又∵NC 平面ONC,∴OA⊥NC,
由CN∥PQ知PQ⊥OA.【变式训练】如图,
在底面为平行四边形的四棱锥P-ABCD
中,AB⊥AC,PA⊥平面ABCD,点E是
PD的中点.
(1)求证:AC⊥PB.
(2)求证:PB∥平面AEC. 【解题提示】(1)要证AC⊥PB,只需证AC⊥平面PAB.
(2)要证PB∥平面AEC,只要利用平行四边形的性质,连接BD与AC相交,就可以在△PBD中证明线线平行,进而证明线面平行.【证明】(1)∵PA⊥平面ABCD,AC 平面ABCD,
∴PA⊥AC.
又∵AB⊥AC,PA∩AB=A,PA 平面PAB,
AB 平面PAB,∴AC⊥平面PAB,∴AC⊥PB.(2)连接BD交AC于点O,并连接EO.
∵四边形ABCD为平行四边形.
∴O为BD的中点.又∵E为PD的中点,
∴在△PDB中EO为中位线,EO∥PB.
∵PB 平面AEC,EO 平面AEC,
∴PB∥平面AEC .【例】如图所示,四边形ABCD为正方形,
SA⊥平面ABCD,过点A且垂直于SC的平面
分别交SB、SC、SD于点E、F、G.
求证:AE⊥SB.
【审题指导】证明本题的关键是要分析出由SA⊥平面ABCD及ABCD是正方形可证BC⊥平面SAB.【规范解答】∵SA⊥平面ABCD,BC? 平面ABCD,
∴SA⊥BC.
又∵BC⊥AB,SA∩AB=A,∴BC⊥平面SAB,
又∵AE 平面SAB,∴BC⊥AE.
∵SC⊥平面AEFG,AE 平面AEFG,∴SC⊥AE.
又∵BC∩SC=C,∴AE⊥平面SBC,
∴AE⊥SB.【变式备选】如图,已知矩形ABCD,
过点A作SA⊥平面ABC,再过点A作AE
⊥SB于点E,过点E作EF⊥SC于点F.
(1)求证:AF⊥SC;
(2)若平面AEF交SD于点G,求证:AG⊥SD.【证明】(1)∵SA⊥平面ABC,BC 平面ABC,
∴SA⊥BC.
∵四边形ABCD是矩形,∴AB⊥BC.
∵AB∩SA=A,∴BC⊥平面SAB.
∵AE 平面SAB,∴BC⊥AE.∵SB⊥AE,BC∩SB=B,
∴AE⊥平面SBC,∴AE⊥SC.
∵EF⊥SC,AE∩EF=E,
∴SC⊥平面AEF.
∵AF 平面AEF,∴AF⊥SC.(2)∵SA⊥平面ABC,DC 平面ABC,∴SA⊥DC.
∵四边形ABCD为矩形,
∵AD⊥DC,SA∩AD=A,∴DC⊥平面SAD.
∵AG 平面SAD,∴DC⊥AG.
由(1)可知SC⊥平面AEF,AG 平面AEF,
∴SC⊥AG.
∵SC∩DC=C,∴AG⊥平面SDC.
∵SD 平面SCD,∴SD⊥AG.1.直线与平面垂直的性质
(1)证明线线平行:若l⊥α,m⊥α,则l∥m.
(2)证明线线垂直:若l⊥α,m α,则l⊥m.
(3)证明面面平行:若l⊥α,l⊥β,则α∥β.
(4)证明线面垂直:①若l∥m,l⊥α,则m⊥α.
②若l⊥α,α∥β,则l⊥β.线面垂直性质的综合应用2.线面垂直与平行的相互转化
(1)空间中直线与直线垂直,直线与平面垂直,直线与平面平行,直线与直线平行可以相互转化,每一种垂直与平行的判定都是从某种垂直与平行开始转化为另一种垂直与平行,最终达到目的.
(2)转化关系
“平行关系”与“垂直关系”在特定条件下是可以相互转化的.【例3】如图,在
多面体ABCDEF中,四边形ABCD是正
方形,AB=2EF=2,EF∥AB,EF⊥FB,
∠BFC=90°,BF=FC,H为BC的中点,
(1)求证:FH∥平面EDB;
(2)求证:AC⊥平面EDB;
【审题指导】(1)可以根据EF∥AB作辅助线,在平面EDB中作直线与FH平行,(2)在(1)的基础上利用EF⊥FB,可以先推出EF⊥平面BFC,由此进一步思考如何证明AC⊥平面EDB.【规范解答】(1)连接AC与BD交于点G,则G为AC的中点,连
接EG、GH,由于H为BC的中点,故GH AB.
又∵EF AB,∴GH EF,
∴四边形EFHG为平行四边形.
∴EG∥FH,而EG 平面EDB,FH 平面EDB.
∴FH∥平面EDB.(2)由四边形ABCD为正方形知AB⊥BC,
又∵EF∥AB,∴EF⊥BC,而EF⊥FB,且BC∩FB=B,
∴EF⊥平面BFC,∴EF⊥FH,∴AB⊥FH.
∵BF=FC,H为BC的中点,
∴FH⊥BC,且BC∩AB=B,
∴FH⊥平面ABCD,∴FH⊥AC.
又∵FH∥EG,∴AC⊥EG.
又∵AC⊥BD,且EG∩BD=G,∴AC⊥平面EDB.【变式训练】如图所示的几何体是将高为
2,底面半径为1的直圆柱沿过轴的平面切开后,将其中一半
沿切面向右水平平移后得到的.A,A′,B,B′分别为CD,
的中点,O1,O1′,O2,O2′分别为CD,
C′D′,DE,D′E′的中点.(1)证明:O1′,A′,O2,B四点共面;
(2)设G为AA′中点,延长A′O1′到H′,使得O1′H′= A′O1′.
证明:BO2′⊥平面H′B′G′.【证明】(1)由已知得,O1′A′∥O2′B′,O2′B′∥O2B.
得O1′A′∥O2B,所以O1′A′与O2B确定一个平面α,且O1′,A′,O2,B都在平面α内,即O1′,A′,O2,B四点共面.(2)如图,延长AO1到I使AO1=O1I,连接IH′及IO1′,由已知可得H′B′⊥平面A′AIH′,从而H′B′⊥IO1′,又在矩形A′AIH ′中O1′、G分别为边A′H′与AA′的中点,所以IO1′⊥H′G,所以IO1′⊥平面H′B′G.
连接IB,则IBO2′O1′
为矩形,所以BO2′∥
IO1′,所以BO2′⊥平
面H′B′G.【典例】(12分)图1,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的主视图和左视图如图2所示.
(1)证明:AD⊥平面PBC;
(2)在∠ACB的平分线上确定一点Q,使得PQ∥平面ABD,并求此时PQ的长.【审题指导】(1)由主视图和左视图可知PA=AC=4,D为PC的中点,进一步可得AD⊥PC.另一方面可通过证BC⊥平面PAC,得BC⊥AD;(2)将问题转化到直角三角形中,利用勾股定理求解.【规范解答】(1)因为PA⊥平面ABC,所以PA⊥BC,
又∵AC⊥BC,PA∩AC=A,∴BC⊥平面PAC,
……………………………………………………………2分∴BC⊥AD. ………………………………………………3分
由三视图可得,在△PAC中,PA=AC=4,
D为PC的中点,∴AD⊥PC,∵BC∩PC=C. ……………4分
∴AD⊥平面PBC. ………………………………………5分(2)取AB的中点O,连接CO并延长至Q,
使得CQ=2OC,点Q即为所求. …………………………6分
∵O为CQ的中点,连接PQ,OD,∴PQ∥OD,
∵PQ? 平面ABD,OD 平面ABD,
∴PQ∥平面ABD,………………………………………8分连接AQ,BQ,因为四边形ACBQ的对角线互相平分,
∴四边形ACBQ为平行四边形,所以AQ=4,
……………………………………………………………10分
又PA⊥平面ABC,AQ 平面ABC,∴PA⊥AQ,
∴在Rt△PAQ中,
…………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】四棱锥P-ABCD的三视图如图,四边形ABCD为正方形,E是侧棱PC上的动点,试问不论点E在何位置,是否都有BD⊥AE?证明你的结论.【解析】不论点E在何位置,都有BD⊥AE.
证明如下:连接AC.
∵四边形ABCD是正方形,∴BD⊥AC.
∵PC⊥底面ABCD且BD 平面ABCD,∴BD⊥PC.
又∵AC∩PC=C,∴BD⊥平面PAC.
∵不论点E在何位置,AE 平面PAC总成立,
∴都有BD⊥AE.1.正方体ABCD-A1B1C1D1中,E为A1C1的中点,则直线CE垂直于( )
(A)AC (B)BD
(C)A1D1 (D)A1A
【解析】选B.因为BD⊥平面AA1C1C,CE 平面AA1C1C,所以CE⊥BD.2.若a,b表示直线,α表示平面,下列说法正确的序号是__________.
①若a⊥α,b∥α,则a⊥b; ②若a⊥α,a⊥b,则b∥α;
③若a∥α,a⊥b,则b⊥α.
【解析】由线面垂直的性质知①正确.②中b可能满足
B α,故②错误;③中b可能与α相交(不垂直),也可能
与α平行,故③错误.
答案:①3.在Rt△ABC中,D是斜边AB的中点,AC=6,BC=8,EC⊥平面ABC,且EC=12,则ED=__________.
【解析】∵EC⊥平面ABC,∴EC⊥CD.
∵在Rt△ABC中, AC=6,BC=8,∴AB=10.
又∵D是斜边AB的中点,
∴在Rt△ECD中,
答案:134.地面上有两根旗杆,底端相距a米,它们的高分别是b米和c米(b>c),则它们顶端的距离为___________.
【解析】如图,由于两旗杆都与地面垂
直,故两旗杆AD与BC平行,且四边形
ABCD是直角梯形,AD=c,BC=b,过D作
DE⊥BC于E,则DE=a,CE=b-c,
答案: 5.在长方体ABCD-A1B1C1D1中,E∈平面ABCD,F∈平面A1B1C1D1,
且EF⊥平面ABCD,求证A1F AE.【证明】如图所示,由长方体的性质可知,AA1⊥平面ABCD.
又∵EF⊥平面ABCD,
∴EF∥AA1,故EF与AA1确定一个平面AEFA1.
∵平面AEFA1∩平面A1B1C1D1=A1F,
平面AEFA1∩平面ABCD=AE.
平面ABCD∥平面A1B1C1D1,∴A1F∥AE,
∴四边形AEFA1为平行四边形,
∴A1F AE.一、选择题(每题4分,共16分)
1.已知α,β是平面,m,n是直线,则下列说法中不正确的是( )
(A)若m∥n,m⊥α,则n⊥α
(B)若m∥α,α∩β=n,则m∥n
(C)若m⊥α,m⊥β,则α∥β
(D)若m⊥α,m β,则α⊥β【解析】选B.A正确,若m∥n,m⊥α,则n与平面α内的任意一条直线垂直,故n⊥α.B错误, 应该是当m∥α,α∩β=n,且m β时,m∥n. C正确,如图所示,过m作平面γ和平面δ,可证γ与α、β的交线都与m垂直,又都在同一平面内,故平行.同理δ与α、β的交线也互相平行,所以α∥β.D正确.2. 点A、B在平面α的同侧,点C
是线段AB的中点,过A、B、C三点
分别作AA1,BB1,CC1与平面α垂直,
垂足分别为A1,B1,C1,若AA1=3,
CC1=5,则BB1=( )
(A)1 (B)7
(C)1或7 (D)8【解析】选B.∵AA1⊥α,BB1⊥α,CC1⊥α,
∴AA1∥BB1∥CC1.
又AA1=3,CC1=5,
∴CC1是梯形AA1B1B的中位线,
∴BB1=2CC1-AA1=2×5-3=7.3.如图,△ABC中,∠ACB=90°,直线l
过点A且垂直于平面ABC,动点P∈l,
当点P逐渐远离点A时,∠PCB的大小
( )
(A)变大 (B)变小
(C)不变 (D)有时变大有时变小【解析】选C.∵l⊥平面ABC,∴BC⊥l.
∵∠ACB=90°,∴BC⊥AC.
又l∩AC=A,∴BC⊥平面PAC,
∴BC⊥PC,∴∠PCB=90°.4.如图,正方体ABCD-A1B1C1D1的棱长为1,E、F分别是BC,DD1上的点,如果B1E⊥平面ABF,则E、F满足的条件一定是
( )
(B)CE+DF=1
(C)CE+D1F=1
(D)E、F在棱BC、DD1上的任意位置【解析】选B.在平面BB1C1C内作BF′∥AF交CC1于点F′.
∵B1E⊥平面ABF,∴B1E⊥AF,
∴B1E⊥BF′,DF=CF′.
在正方形BB1C1C中,
由B1E⊥BF′得CE=C1F′=1-CF′,
∴CE+CF′=1,即CE+DF=1.二、填空题(每题4分,共8分)
5.如图,AB
是⊙O的直径,C是圆周上不同于A、
B的点,PA垂直于⊙O所在的平面,
AE⊥PB于E,AF⊥PC于F.因此
__________⊥平面PBC.(请填图上
的一条直线)【解析】∵PA垂直于⊙O所在的平面,BC在⊙O所在的平面内,∴PA⊥BC.
∵C是圆周上不同于A、B的点,∴BC⊥AC.
又PA∩AC=A,∴BC⊥平面PAC.
又AF 平面PAC,∴BC⊥AF.
∵AF⊥PC且BC∩PC=C,∴AF⊥平面PBC.
答案:AF6.如图,PA⊥平面ABC,∠ACB=90°,EF∥PA,则图中直角三角形的个数是__________.【解析】由PA⊥平面ABC,得PA⊥AB,PA⊥AC,PA⊥BC.
又∵BC⊥AC,AC∩PA=A,∴BC⊥平面PAC,∴BC⊥PC.
∵EF∥PA,PA⊥平面ABC,∴EF⊥平面ABC,∴EF⊥BE,EF⊥EC,
∴△PAB、△PAC、△ABC、△PBC、△EFC、△BEF均为直角三角形.
答案:6
【易错提醒】△PBC是直角三角形容易漏掉,原因是未分析出BC⊥平面PAC这一条件.三、解答题(每题8分,共16分)
7.如图,在直三棱柱ABC-A1B1C1中,
AC=9,BC=12,AB=15,AA1=12.
求证:AC⊥B1C.
【解题提示】要证明AC⊥B1C,根据题目条件只要证明
AC⊥平面BB1C1C.【证明】∵AC=9,BC=12,AB=15,
∴AB2=AC2+BC2,∴∠ACB=90°,AC ⊥BC.
∵CC1⊥平面ABC,AC 平面ABC.
∴AC⊥CC1,又CC1∩BC=C,
∴AC⊥平面BB1C1C .
∵B1C 平面BB1C1C, ∴AC⊥B1C.8.如图所示,在正方体ABCD-A1B1C1D1中,
M是AB上一点,N是A1C的中点,
MN⊥平面A1DC.
求证:(1)MN∥AD1;
(2)M是AB的中点.【证明】(1)∵ADD1A1为正方形,∴AD1⊥A1D.
又∵CD⊥平面ADD1A1,AD1 平面ADD1A1,
∴CD⊥AD1.
∵A1D∩CD=D,
∴AD1⊥平面A1DC.
又∵MN⊥平面A1DC,
∴MN∥AD1.(2)连接ON,在△A1DC中,
A1O=OD,A1N=NC.
∴ON CD AB,
∴ON∥AM.
又∵MN∥OA,∴四边形AMNO为平行四边形,
∴ON=AM.
∴M是AB的中点. 【方法技巧】解读线面垂直的性质的应用
学习线面垂直的性质的意义在于建立“平行关系”与“垂直关系”的相互转化意识.因此通过性质的学习,可以让我们对空间点、线、面的位置关系有一个更为全面、系统的认识.
在应用线面垂直的性质时,要注意尽量多地分析出题目条件中所隐含的线面垂直、线线平行、面面平行等位置关系,同时要根据题目所证结论设计证明思路.【挑战能力】
(10分)已知AA1⊥平面ABC,
AB=BC=AA1=CA,P为A1B上的点.
(1)当P为A1B中点时,求证:
AB⊥PC;
(2)当二面角P-AC-B的大小为60°时,
求 的值.【解析】(1)当 时,作PD∥AA1交AB于D,
连接CD.
由AA1⊥平面ABC,
知PD⊥平面ABC.
当P为A1B中点时,D为AB中点.
∵△ABC为正三角形,
∴CD⊥AB,∴AB⊥平面PCD,∴PC⊥AB.(2)过D作DE⊥AC于E,连接PE,则PE⊥AC,
∴∠DEP为二面角P-AC-B的平面角,即
∵PD∥A1A,AA1=AB,∴PD=BD,AA1=AB,
