1.7.1 简单几何体的侧面积 课件4
图片预览










文档简介
课件74张PPT。1.7.1 简单几何体的侧面积1.圆柱、圆锥、圆台的侧面积的求法
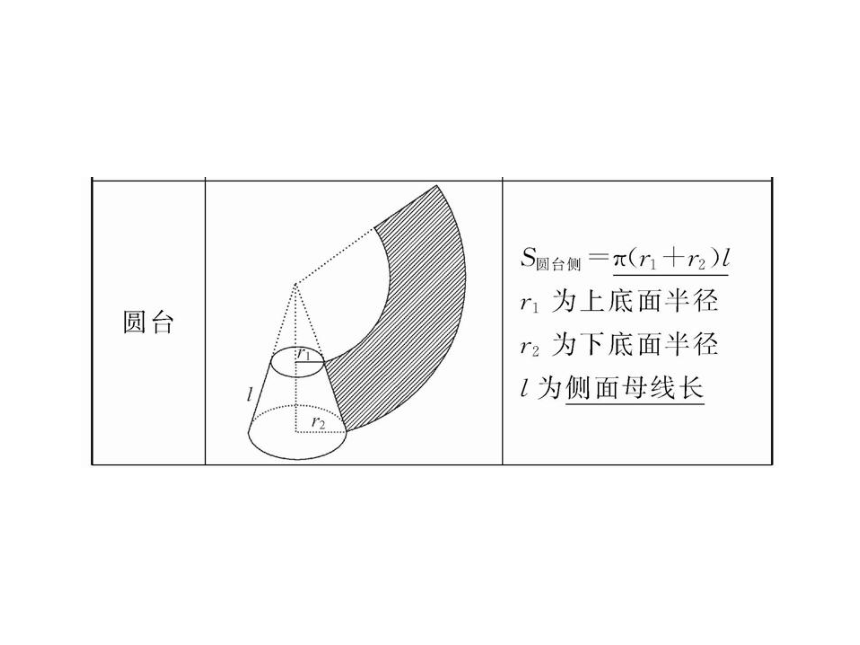
由圆柱的侧面积公式可知,要求其侧面积,必须已知(或能求出)它的底面圆的半径和它的母线长.
要求圆锥的侧面积应已知它的母线长和底面圆的半径.
要求圆台的侧面积应已知圆台的母线长和上、下两底面圆的半径.简单旋转体的侧面积 2.圆柱、圆锥、圆台的侧面积之间的关系
旋转体中轴截面可以将母线、底面半径、高等主要元素联系在一起,因此处理好轴截面中的边角关系是正确计算的关键.【例1】如图所示,为
了制作一个圆柱形灯笼,先要制作4个全
等的矩形骨架,总计耗用9.6米铁丝,再
用S平方米塑料片制成圆柱的侧面和下底
面(不安装上底面).
(1)当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米);
(2)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出灯笼的三视图(作图时,不需考虑骨架等因素).【审题指导】根据总计耗用9.6米铁丝可以推出圆柱的高与底面半径之间的关系,以及半径r的取值范围. 另外要注意到S是由圆柱的侧面和圆柱的一个底面组成的.【规范解答】(1)设圆柱形灯笼的高为h,则4(4r+2h)=9.6,
所以h=1.2-2r,
所以S=S底面+S侧面=πr2+2πrh
=πr2+2πr(1.2-2r)
=2.4πr-3πr2(0所以,当 (米)时S有最大值.
最大值为2.4π×0.4-3π×0.42≈1.51(平方米).(2)由(1)知r=0.3(米)时,h=0.6(米).其主视图与左视图均为边长是0.6米的正方形,俯视图是直径为0.6米的圆.如图:【变式训练】已知圆台的上、下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.
【解析】设圆台的母线长为l,则
S圆台侧=π(r1+r2)l=π(2+5)l=7πl.
两底面的面积之和为πr12+πr22=π×22+π×52=29π.
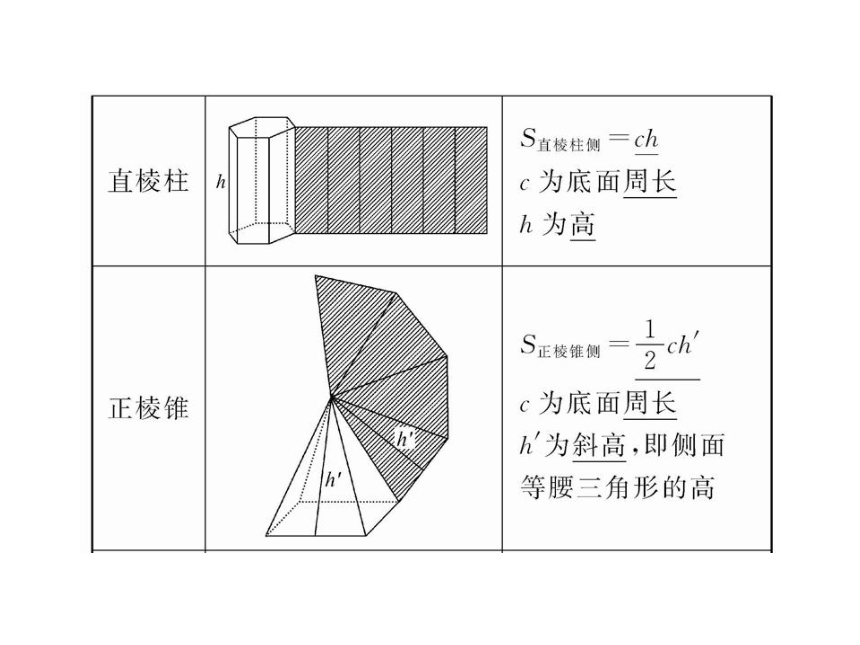
由题意知7πl=29π.1.正棱柱、正棱锥、正棱台的侧面积之间的关系简单多面体的表面积2.简单多面体的侧面积的求法
(1)关键:找到多面体的特征几何图形,如棱柱中的矩形,棱台中的直角梯形,棱锥中的直角三角形,它们是联系高与斜高、侧棱、底面边长间的桥梁,架起了求侧面积公式中未知量与条件中已知几何元素间的桥梁.(2)策略:①正棱柱、正棱锥、正棱台的所有侧面的面积都相等,因此求侧面积时,可先求一个侧面的面积,然后乘以侧面的个数.
②解决台体的问题,通常要补上截去的小棱锥,寻找上下底面之间的关系.
棱柱的侧面积不一定等于底面周长和侧棱长的乘积,只有直棱柱的侧面积等于底面周长与侧棱长的乘积.【例2】正四棱锥底面正方形的边长为4 cm,高与斜高的夹角为30°,求正四棱锥的侧面积和表面积.
【审题指导】审题时要画出正四棱锥的高、斜高、底面正方形的边心距组成的直角三角形,在此三角形中计算正四棱锥的关键量.【规范解答】如图,正棱锥的高PO、斜高PE、底面边心距OE组成Rt△POE.
∠OPE=30°.
又S底=42=16(cm2),
∴S表=S侧+S底=32+16=48(cm2).【互动探究】把本题中的条件“高与斜高的夹角为30°”改为“高与侧棱的夹角为30°”应如何解答?
【解题提示】△POB和△PBE都是直角三角形,通过解这两个三角形求出正四棱锥的斜高,进而计算侧面积和表面积.【解析】正棱锥的高PO、侧棱PB、底面线段OB组成Rt△POB.
其中
在Rt△PBE中,BE=2 (cm), ∠PEB=90°,1.求组合体的表面积的基本步骤
(1)首先要弄清楚它是由哪些基本几何体构成的,组成形式是什么.
(2)其次根据组合体的组成形式设计计算思路.
(3)最后根据公式计算求值.组合体的表面积 2.求组合体的表面积的解题策略
(1)对于由基本几何体拼接成的组合体,要注意拼接面重合对组合体表面积的影响.
(2)对于从基本几何体中切掉或挖掉的部分构成的组合体,要注意新产生的截面和原几何体的表面的变化.【例3】如图,△ABC中,AC=3,BC=4,AB=5,
以AB所在直线为轴,三角形面绕轴旋转一周形
成一旋转体,求此旋转体的表面积.
【审题指导】该旋转体是一个组合体,由两部
分组成,上部为圆锥,下部为与上部同底面的
另一圆锥.【规范解答】过C点作CD⊥AB,垂足为D.△ABC
以AB所在直线为轴旋转一周,所得到的旋转体
是两个底面重合的圆锥,如图所示,这两个圆
锥的高的和为AB=5,底面半径
故
即所得旋转体的表面积为 【变式训练】一个几何体的直观图如图,求该几何体的表面积.
【解题提示】此几何体的表面积等于下面长方体的全面积加上面圆柱的侧面积.【解析】由几何体的直观图可知,该几何体上面是一个圆柱,下面是一个长方体,其表面积等于下面长方体的全面积加上面圆柱的侧面积.其中下面的长方体的长、宽、高分别为8、8、4, 上面的圆柱的底面直径为4,高为8,所以该几何体的表面积为2(8×8+8×4+8×4)+π×4×8=256+32π. 展开图问题的解题方法
(1)基本思想:曲面上有关距离的问题,往往需根据侧面展开图来处理.
(2)基本方法:解答几何体表面上两点间最短线路问题,一般都是将几何体表面展开,转化为求平面内两点间线段的长.
(3)有关知识:两点之间线段最短;解直角三角形等有关知识.展开图问题【例】如图所示,长方体ABCD-
A1B1C1D1中,AB=a,BC=b,BB1=c,
并且a>b>c>0.求沿着长方体的
表面自A点到C1点的最短线路的长.
【审题指导】沿着长方体的表面自A点到C1点由以下三种可能:(1)沿平面AA1B1B、平面BB1C1C,(2)沿平面AA1B1B、平面A1B1C1D1,(3)沿平面ABCD、平面BB1C1C.【规范解答】将长方体相邻两个面展开有下列三种可能.如图所示图(1)、(2)、(3)中AC1的长分别为
∵a>b>c>0,∴ab>ac>bc>0,
故最短线路的长为 【变式备选】如图所示,在直三棱柱ABC-A1B1C1中,
∠ABC=90°,E、F分别为AA1、C1B1的中点,求沿棱柱的表面从E点到F点的最短路径的长度.【解析】将三棱柱的侧面、底面展开有三种情形,如图所示.在(1)中,
在(2)中,取B1B的中点G,连接EG,则EG⊥B1B,
故
在(3)中,作EG∥A1C1,FG∥A1A,交点为G,则易知EG⊥FG,故
比较后可知,如图(3)所示的E点到F点的路线最短.【典例】(12分)一个几何体的三视图如图所示,其中主视图中△ABC是边长为2的正三角形,俯视图为正六边形,求该几何体的表面积.【审题指导】审题时要注意以下信息:(1)几何体是正六棱锥;(2)正六棱锥的底面是正六边形,其边长为1,侧棱长为2.求该几何体的表面积时需先求底面积和侧面积,然后求和即可.【规范解答】由三视图可知该几何体是正六棱锥(如图),
其底面边长为 ……………………2分
侧棱长为AC=2, ……………………………………4分斜高
……………………………………………………………6分
…………………………8分
………………………… 10分
……………………………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】一个几何体的三视图如图,求该几何体的表面积.【解析】由几何体的三视图可知,该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的侧面积.其中下面长方体的
长、宽、高分别为8、10、2,
上面的长方体的长、宽、高分
别为6、2、8,所以该几何体的
表面积为2(8×10+8×2+10×
2)+2(6×8+2×8)=360.1.下图不是棱柱的展开图的是( )【解析】选C.观察可知选项C,不是棱柱的展开图.2.一个边长为a的正方体,切成27个全等的小正方体,则表面积增加了( )
(A)6a2 (B)12a2
(C)18a2 (D)24a2
【解析】选B.切成27个小正方体后,每个正方体的棱长为
故表面积为 而原来的表面积是
6a2,故增加了12a2.3.已知圆锥的母线长为5,底面半径为3,则圆锥侧面积为
( )
(A)15π (B)24π
(C)30π (D)39π
【解析】选A.S圆锥侧=π×3×5=15π.4.如图所示,一个圆柱的底面半径为3,
高为5,O、O′分别为上、下两个底面圆
的圆心,AA′、BB′为两条母线,用平
面AA′O′O,平面BB′O′O截此圆柱,
其中∠AOB=∠A′O′B′=60°,剩余几
何体的表面积为__________.
【解析】
答案:40π+305.圆台的较小底面半径为1,母线长为2,一条母线和底面的一条半径有交点且成60°,则圆台的侧面积为______.
【解析】由题意得,圆台的上、下底面半径r1=1,r2=2,母线l=2,S圆台侧=π(r1+r2)l=6π.
答案:6π6.如图所示,一个简单的空间几何体的主视图和左视图均是边长为2的正三角形,俯视图轮廓为正方形,试描述该几何体的特征,并求该几何体的表面积.【解析】该几何体为底面是边长为2的正方形,高为 的正四棱锥.
四棱锥的侧面是全等的等腰三角形,设其高为h′,
则
∴该几何体的表面积为12.一、选择题(每题4分,共16分)
1.某同学制作了一个对面图案
相同的正方体礼品盒(如图),
则这个正方体礼品盒的表面
展开图应该为( )
【解析】选A.观察可知B、
C、D选项不符合对面图案相同.2.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为( )
(A)1 (B)2
【解析】选B.设圆锥的底面半径为r,母线长为l,
则由题意得πl=2πr,∴l=2r,又∵πr2+πrl=3π,
∴3πr2=3π,∴r2=1,r=1(-1舍去).
∴圆锥的底面直径为2.3.圆柱的一个底面面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是( )
(A)πS (B)2πS
(C)4πS
【解析】选C.设圆柱的底面半径为r,则由题意得母线长为2πr,又∵πr2=S,∴S侧=(2πr)2=4πS.4.若一个底面是正三角形的三棱柱的主视图如图所示,则其侧面积等于( )
(A) (B)2 (C)2 (D)6
【解题提示】把三视图恢复成直观图,求出各个侧面的侧面积,进而求出总的侧面积.【解析】选D.三棱柱的直观图如图,其底面是边长为2的正三角形,侧棱长为1的正三棱柱,
∴S侧=(1×2)×3=6.二、填空题(每题4分,共8分)
5.已知一个几何体的三视图如图所示,则此几何体的表面积是__________.【解析】
S圆柱侧=2π×a×2a=4πa2,S底面=πa2,
∴S表面=S圆锥侧+S圆柱侧+S底面
答案: 6.正四棱台的高是12 cm,两底面边长相差10 cm,表面积是512 cm2,则正四棱台的侧面积为__________.【解析】如图所示,O′、O分别为
上、下底面中心,则O′O=12 cm,
分别取B′C′、BC的中点E′、E,
过点E′作E′F⊥OE于点F.
设上、下底面边长分别为a cm、
b cm,故b-a=10. ①在Rt△E′EF中,E′F=O′O=12 cm,
则斜高E′E=13 cm.
由
即有a2+b2+2(a+b)·13=512,结合①可得a=2,b=12,
则
答案:364 cm2 【方法技巧】棱锥、棱台中的重要图形
1.棱台中三个重要的直角梯形,如本题中的直角梯形O′E′EO、B′E′EB,O′B′BO,因为它们和台体的特征量(上下底边长、高、斜高)紧密相关,所以做此类题目时关键是要作出示意图,将与解题有关的特征量,转化到同一直角梯形中求解.2.正棱锥中几个重要的直角三角形
(1)侧棱、高、底面正多边形外接圆的半径构成的直角三角形;
(2)侧棱、斜高、底面边长的一半构成的直角三角形;
(3)斜高、高、边心距构成的直角三角形.三、解答题(每题8分,共16分)
7.直角梯形的一个底角为45°,下底长为上底长的 这
个梯形绕下底所在直线旋转一周所成的旋转体的表面积是
求这个旋转体的体积.
【解题提示】先根据表面积建立方程,求出计算体
积时所需的关键量,再求体积.【解析】如图所示,梯形ABCD中,
AB∥CD,∠A=90°,∠B=45°,
绕AB边旋转一周后形成一圆柱和一
圆锥的组合体.
设CD=x,则S表=S圆柱底+S圆柱侧+S圆锥侧=
π·AD2+2π·AD·CD+π·AD·BC
由题意得, 则x=2,
CD=2,AB=3.
V=V圆柱+V圆锥 【方法技巧】方程思想在几何体体积计算中的妙用
此类已知旋转体(或其他几何体)表面积(或体积)的问题,常利用方程思想,先通过分析题目条件选出与该几何体关键量联系最密切的量作为未知数.列方程求出各关键量的值.8.如图所示是某几何体的三视图,试根据三视图求该几何体的表面积.【解析】此几何体是四棱锥,作出其直观图,如图所示,
由三视图可知四棱锥P-ABCD中,底面四边形ABCD是矩形,
PO⊥平面ABCD,O是AD的中点.且AB=CD=2,AD=BC=6,PO=4.
易证PD⊥CD,PA⊥AB,取BC的中点E,连接OE、PE,则BC⊥平面POE,∴BC⊥PE.且
PD=PA=5,
同样得S△PCD=5,
S矩形ABCD=6×2=12,∴该几何体的表面积
【误区警示】解答本题容易出现以下两个错误:(1)误认为AB=AD=4,(2)△PBC底边BC上的高PE求错.【挑战能力】
(10分)如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D、E分别是CC1、BC的中点,AE=DE.
(1)求此正三棱柱的侧棱长.
(2)求正三棱柱ABC-A1B1C1的表面积.【解析】(1)设正三棱柱ABC-A1B1C1的侧棱长为x,
∵△ABC是正三角形,∴AE⊥BC.
又底面ABC⊥侧面BB1C1C,且交线为BC,
∴AE⊥侧面BB1C1C.
由AE=DE,在Rt△ECD中,得
解得 即正三棱柱的侧棱长为 (2)S=S侧+S底,
由圆柱的侧面积公式可知,要求其侧面积,必须已知(或能求出)它的底面圆的半径和它的母线长.
要求圆锥的侧面积应已知它的母线长和底面圆的半径.
要求圆台的侧面积应已知圆台的母线长和上、下两底面圆的半径.简单旋转体的侧面积 2.圆柱、圆锥、圆台的侧面积之间的关系
旋转体中轴截面可以将母线、底面半径、高等主要元素联系在一起,因此处理好轴截面中的边角关系是正确计算的关键.【例1】如图所示,为
了制作一个圆柱形灯笼,先要制作4个全
等的矩形骨架,总计耗用9.6米铁丝,再
用S平方米塑料片制成圆柱的侧面和下底
面(不安装上底面).
(1)当圆柱底面半径r取何值时,S取得最大值?并求出该最大值(结果精确到0.01平方米);
(2)若要制作一个如图放置的,底面半径为0.3米的灯笼,请作出灯笼的三视图(作图时,不需考虑骨架等因素).【审题指导】根据总计耗用9.6米铁丝可以推出圆柱的高与底面半径之间的关系,以及半径r的取值范围. 另外要注意到S是由圆柱的侧面和圆柱的一个底面组成的.【规范解答】(1)设圆柱形灯笼的高为h,则4(4r+2h)=9.6,
所以h=1.2-2r,
所以S=S底面+S侧面=πr2+2πrh
=πr2+2πr(1.2-2r)
=2.4πr-3πr2(0
最大值为2.4π×0.4-3π×0.42≈1.51(平方米).(2)由(1)知r=0.3(米)时,h=0.6(米).其主视图与左视图均为边长是0.6米的正方形,俯视图是直径为0.6米的圆.如图:【变式训练】已知圆台的上、下底面半径分别是2、5,且侧面面积等于两底面面积之和,求该圆台的母线长.
【解析】设圆台的母线长为l,则
S圆台侧=π(r1+r2)l=π(2+5)l=7πl.
两底面的面积之和为πr12+πr22=π×22+π×52=29π.
由题意知7πl=29π.1.正棱柱、正棱锥、正棱台的侧面积之间的关系简单多面体的表面积2.简单多面体的侧面积的求法
(1)关键:找到多面体的特征几何图形,如棱柱中的矩形,棱台中的直角梯形,棱锥中的直角三角形,它们是联系高与斜高、侧棱、底面边长间的桥梁,架起了求侧面积公式中未知量与条件中已知几何元素间的桥梁.(2)策略:①正棱柱、正棱锥、正棱台的所有侧面的面积都相等,因此求侧面积时,可先求一个侧面的面积,然后乘以侧面的个数.
②解决台体的问题,通常要补上截去的小棱锥,寻找上下底面之间的关系.
棱柱的侧面积不一定等于底面周长和侧棱长的乘积,只有直棱柱的侧面积等于底面周长与侧棱长的乘积.【例2】正四棱锥底面正方形的边长为4 cm,高与斜高的夹角为30°,求正四棱锥的侧面积和表面积.
【审题指导】审题时要画出正四棱锥的高、斜高、底面正方形的边心距组成的直角三角形,在此三角形中计算正四棱锥的关键量.【规范解答】如图,正棱锥的高PO、斜高PE、底面边心距OE组成Rt△POE.
∠OPE=30°.
又S底=42=16(cm2),
∴S表=S侧+S底=32+16=48(cm2).【互动探究】把本题中的条件“高与斜高的夹角为30°”改为“高与侧棱的夹角为30°”应如何解答?
【解题提示】△POB和△PBE都是直角三角形,通过解这两个三角形求出正四棱锥的斜高,进而计算侧面积和表面积.【解析】正棱锥的高PO、侧棱PB、底面线段OB组成Rt△POB.
其中
在Rt△PBE中,BE=2 (cm), ∠PEB=90°,1.求组合体的表面积的基本步骤
(1)首先要弄清楚它是由哪些基本几何体构成的,组成形式是什么.
(2)其次根据组合体的组成形式设计计算思路.
(3)最后根据公式计算求值.组合体的表面积 2.求组合体的表面积的解题策略
(1)对于由基本几何体拼接成的组合体,要注意拼接面重合对组合体表面积的影响.
(2)对于从基本几何体中切掉或挖掉的部分构成的组合体,要注意新产生的截面和原几何体的表面的变化.【例3】如图,△ABC中,AC=3,BC=4,AB=5,
以AB所在直线为轴,三角形面绕轴旋转一周形
成一旋转体,求此旋转体的表面积.
【审题指导】该旋转体是一个组合体,由两部
分组成,上部为圆锥,下部为与上部同底面的
另一圆锥.【规范解答】过C点作CD⊥AB,垂足为D.△ABC
以AB所在直线为轴旋转一周,所得到的旋转体
是两个底面重合的圆锥,如图所示,这两个圆
锥的高的和为AB=5,底面半径
故
即所得旋转体的表面积为 【变式训练】一个几何体的直观图如图,求该几何体的表面积.
【解题提示】此几何体的表面积等于下面长方体的全面积加上面圆柱的侧面积.【解析】由几何体的直观图可知,该几何体上面是一个圆柱,下面是一个长方体,其表面积等于下面长方体的全面积加上面圆柱的侧面积.其中下面的长方体的长、宽、高分别为8、8、4, 上面的圆柱的底面直径为4,高为8,所以该几何体的表面积为2(8×8+8×4+8×4)+π×4×8=256+32π. 展开图问题的解题方法
(1)基本思想:曲面上有关距离的问题,往往需根据侧面展开图来处理.
(2)基本方法:解答几何体表面上两点间最短线路问题,一般都是将几何体表面展开,转化为求平面内两点间线段的长.
(3)有关知识:两点之间线段最短;解直角三角形等有关知识.展开图问题【例】如图所示,长方体ABCD-
A1B1C1D1中,AB=a,BC=b,BB1=c,
并且a>b>c>0.求沿着长方体的
表面自A点到C1点的最短线路的长.
【审题指导】沿着长方体的表面自A点到C1点由以下三种可能:(1)沿平面AA1B1B、平面BB1C1C,(2)沿平面AA1B1B、平面A1B1C1D1,(3)沿平面ABCD、平面BB1C1C.【规范解答】将长方体相邻两个面展开有下列三种可能.如图所示图(1)、(2)、(3)中AC1的长分别为
∵a>b>c>0,∴ab>ac>bc>0,
故最短线路的长为 【变式备选】如图所示,在直三棱柱ABC-A1B1C1中,
∠ABC=90°,E、F分别为AA1、C1B1的中点,求沿棱柱的表面从E点到F点的最短路径的长度.【解析】将三棱柱的侧面、底面展开有三种情形,如图所示.在(1)中,
在(2)中,取B1B的中点G,连接EG,则EG⊥B1B,
故
在(3)中,作EG∥A1C1,FG∥A1A,交点为G,则易知EG⊥FG,故
比较后可知,如图(3)所示的E点到F点的路线最短.【典例】(12分)一个几何体的三视图如图所示,其中主视图中△ABC是边长为2的正三角形,俯视图为正六边形,求该几何体的表面积.【审题指导】审题时要注意以下信息:(1)几何体是正六棱锥;(2)正六棱锥的底面是正六边形,其边长为1,侧棱长为2.求该几何体的表面积时需先求底面积和侧面积,然后求和即可.【规范解答】由三视图可知该几何体是正六棱锥(如图),
其底面边长为 ……………………2分
侧棱长为AC=2, ……………………………………4分斜高
……………………………………………………………6分
…………………………8分
………………………… 10分
……………………………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】一个几何体的三视图如图,求该几何体的表面积.【解析】由几何体的三视图可知,该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的侧面积.其中下面长方体的
长、宽、高分别为8、10、2,
上面的长方体的长、宽、高分
别为6、2、8,所以该几何体的
表面积为2(8×10+8×2+10×
2)+2(6×8+2×8)=360.1.下图不是棱柱的展开图的是( )【解析】选C.观察可知选项C,不是棱柱的展开图.2.一个边长为a的正方体,切成27个全等的小正方体,则表面积增加了( )
(A)6a2 (B)12a2
(C)18a2 (D)24a2
【解析】选B.切成27个小正方体后,每个正方体的棱长为
故表面积为 而原来的表面积是
6a2,故增加了12a2.3.已知圆锥的母线长为5,底面半径为3,则圆锥侧面积为
( )
(A)15π (B)24π
(C)30π (D)39π
【解析】选A.S圆锥侧=π×3×5=15π.4.如图所示,一个圆柱的底面半径为3,
高为5,O、O′分别为上、下两个底面圆
的圆心,AA′、BB′为两条母线,用平
面AA′O′O,平面BB′O′O截此圆柱,
其中∠AOB=∠A′O′B′=60°,剩余几
何体的表面积为__________.
【解析】
答案:40π+305.圆台的较小底面半径为1,母线长为2,一条母线和底面的一条半径有交点且成60°,则圆台的侧面积为______.
【解析】由题意得,圆台的上、下底面半径r1=1,r2=2,母线l=2,S圆台侧=π(r1+r2)l=6π.
答案:6π6.如图所示,一个简单的空间几何体的主视图和左视图均是边长为2的正三角形,俯视图轮廓为正方形,试描述该几何体的特征,并求该几何体的表面积.【解析】该几何体为底面是边长为2的正方形,高为 的正四棱锥.
四棱锥的侧面是全等的等腰三角形,设其高为h′,
则
∴该几何体的表面积为12.一、选择题(每题4分,共16分)
1.某同学制作了一个对面图案
相同的正方体礼品盒(如图),
则这个正方体礼品盒的表面
展开图应该为( )
【解析】选A.观察可知B、
C、D选项不符合对面图案相同.2.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为( )
(A)1 (B)2
【解析】选B.设圆锥的底面半径为r,母线长为l,
则由题意得πl=2πr,∴l=2r,又∵πr2+πrl=3π,
∴3πr2=3π,∴r2=1,r=1(-1舍去).
∴圆锥的底面直径为2.3.圆柱的一个底面面积为S,侧面展开图是一个正方形,那么这个圆柱的侧面积是( )
(A)πS (B)2πS
(C)4πS
【解析】选C.设圆柱的底面半径为r,则由题意得母线长为2πr,又∵πr2=S,∴S侧=(2πr)2=4πS.4.若一个底面是正三角形的三棱柱的主视图如图所示,则其侧面积等于( )
(A) (B)2 (C)2 (D)6
【解题提示】把三视图恢复成直观图,求出各个侧面的侧面积,进而求出总的侧面积.【解析】选D.三棱柱的直观图如图,其底面是边长为2的正三角形,侧棱长为1的正三棱柱,
∴S侧=(1×2)×3=6.二、填空题(每题4分,共8分)
5.已知一个几何体的三视图如图所示,则此几何体的表面积是__________.【解析】
S圆柱侧=2π×a×2a=4πa2,S底面=πa2,
∴S表面=S圆锥侧+S圆柱侧+S底面
答案: 6.正四棱台的高是12 cm,两底面边长相差10 cm,表面积是512 cm2,则正四棱台的侧面积为__________.【解析】如图所示,O′、O分别为
上、下底面中心,则O′O=12 cm,
分别取B′C′、BC的中点E′、E,
过点E′作E′F⊥OE于点F.
设上、下底面边长分别为a cm、
b cm,故b-a=10. ①在Rt△E′EF中,E′F=O′O=12 cm,
则斜高E′E=13 cm.
由
即有a2+b2+2(a+b)·13=512,结合①可得a=2,b=12,
则
答案:364 cm2 【方法技巧】棱锥、棱台中的重要图形
1.棱台中三个重要的直角梯形,如本题中的直角梯形O′E′EO、B′E′EB,O′B′BO,因为它们和台体的特征量(上下底边长、高、斜高)紧密相关,所以做此类题目时关键是要作出示意图,将与解题有关的特征量,转化到同一直角梯形中求解.2.正棱锥中几个重要的直角三角形
(1)侧棱、高、底面正多边形外接圆的半径构成的直角三角形;
(2)侧棱、斜高、底面边长的一半构成的直角三角形;
(3)斜高、高、边心距构成的直角三角形.三、解答题(每题8分,共16分)
7.直角梯形的一个底角为45°,下底长为上底长的 这
个梯形绕下底所在直线旋转一周所成的旋转体的表面积是
求这个旋转体的体积.
【解题提示】先根据表面积建立方程,求出计算体
积时所需的关键量,再求体积.【解析】如图所示,梯形ABCD中,
AB∥CD,∠A=90°,∠B=45°,
绕AB边旋转一周后形成一圆柱和一
圆锥的组合体.
设CD=x,则S表=S圆柱底+S圆柱侧+S圆锥侧=
π·AD2+2π·AD·CD+π·AD·BC
由题意得, 则x=2,
CD=2,AB=3.
V=V圆柱+V圆锥 【方法技巧】方程思想在几何体体积计算中的妙用
此类已知旋转体(或其他几何体)表面积(或体积)的问题,常利用方程思想,先通过分析题目条件选出与该几何体关键量联系最密切的量作为未知数.列方程求出各关键量的值.8.如图所示是某几何体的三视图,试根据三视图求该几何体的表面积.【解析】此几何体是四棱锥,作出其直观图,如图所示,
由三视图可知四棱锥P-ABCD中,底面四边形ABCD是矩形,
PO⊥平面ABCD,O是AD的中点.且AB=CD=2,AD=BC=6,PO=4.
易证PD⊥CD,PA⊥AB,取BC的中点E,连接OE、PE,则BC⊥平面POE,∴BC⊥PE.且
PD=PA=5,
同样得S△PCD=5,
S矩形ABCD=6×2=12,∴该几何体的表面积
【误区警示】解答本题容易出现以下两个错误:(1)误认为AB=AD=4,(2)△PBC底边BC上的高PE求错.【挑战能力】
(10分)如图,已知正三棱柱ABC-A1B1C1的底面边长是2,D、E分别是CC1、BC的中点,AE=DE.
(1)求此正三棱柱的侧棱长.
(2)求正三棱柱ABC-A1B1C1的表面积.【解析】(1)设正三棱柱ABC-A1B1C1的侧棱长为x,
∵△ABC是正三角形,∴AE⊥BC.
又底面ABC⊥侧面BB1C1C,且交线为BC,
∴AE⊥侧面BB1C1C.
由AE=DE,在Rt△ECD中,得
解得 即正三棱柱的侧棱长为 (2)S=S侧+S底,
