1.7.3 球的表面积和体积 课件2
文档属性
| 名称 | 1.7.3 球的表面积和体积 课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 806.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-22 00:00:00 | ||
图片预览










文档简介
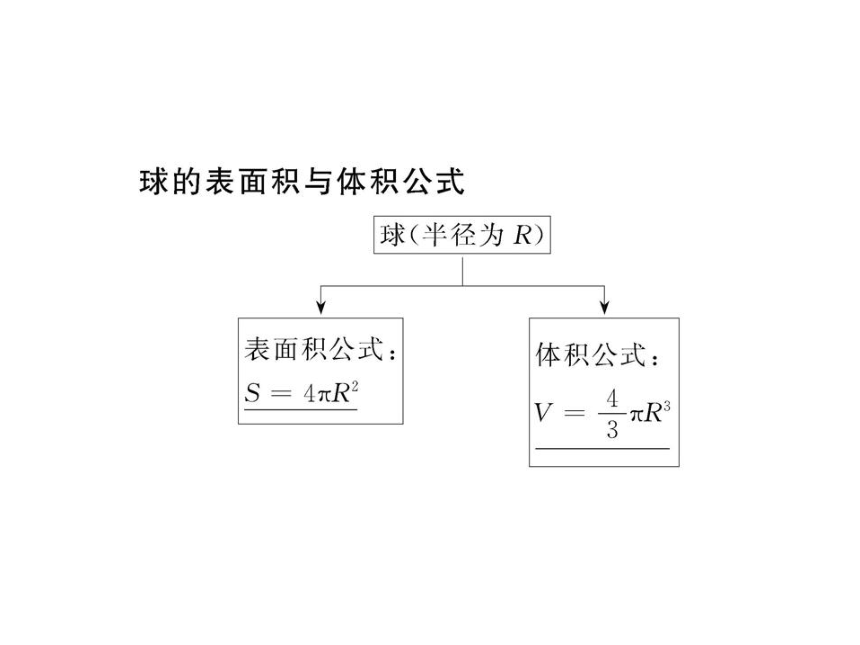
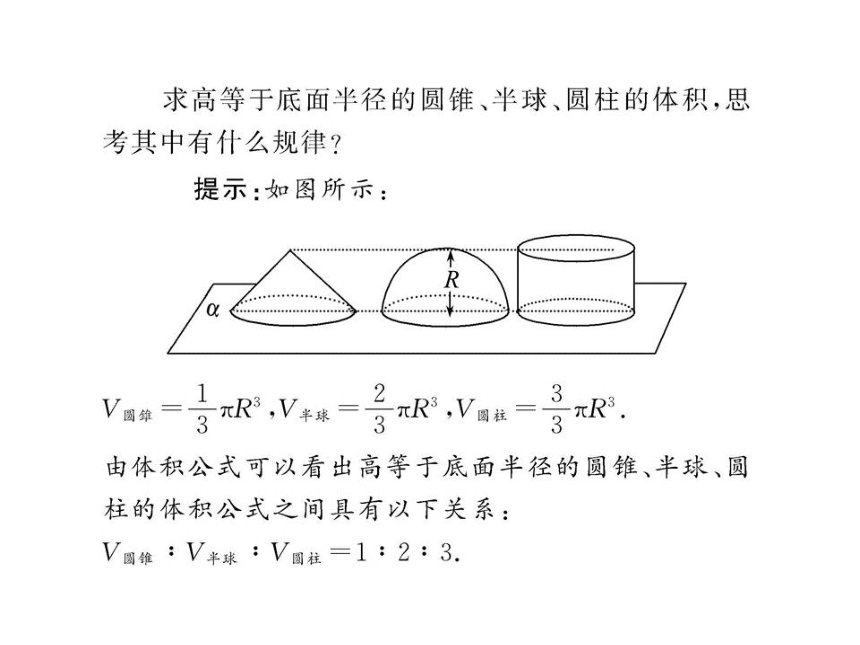
课件67张PPT。1. 计算球的表面积和体积时要注意的问题
(1)关键是计算球的半径,而计算半径的关键是寻找球心的位置.因此,在解题过程中要特别关注题目中所揭示的球心位置,球面上的点等信息.球的表面积和体积 (2)当球的半径增加为原来的2倍时,球的表面积增加为原来的4倍,球的体积增加为原来的8倍.
(3)注意公式的“双向”应用,也就是说当知道球的表面积或体积时,也可以求出球的半径.【例1】请用所学知识探求表面积相等的球和正方体,哪个体积更大.
【审题指导】由球和正方体的表面积相等可以得到球的半径与正方体的棱长之间的关系,将球的体积用正方体的棱长表示出来,就可以进行比较.【规范解答】设球的半径为r,正方体的棱长为a,依题意
得4πr2=6a2,所以
所以
又因为V正方体=a3,且
所以V球>V正方体.
即球的体积大于正方体的体积.【变式训练】若三个球的表面积之比为1∶2∶3,求这三个球的体积之比.
【解题提示】先由球的表面积之比求得半径之比,再求体积之比.【解析】设三个球的半径分别为R1,R2,R3,体积分别为V1,V2,V3,
∵三个球的表面积之比为1∶2∶3,
∴4πR12∶4πR22∶4πR32=R12∶R22∶R32=1∶2∶3,
∴R13∶R23∶R33
即三个球的体积之比为 有关球的截面的性质
(1)用一个平面去截一个球,
截面是圆面.
(2)球心和截面圆圆心的连线
垂直于截面.
(3)球心到截面的距离d与球
的半径R及截面的半径r满足r2=R2-d2,如图所示.球的截面问题【例2】一个球内有相距9 cm的两个平行截面,它们的面积分别为49π cm2和400π cm2,求球的表面积.
【审题指导】本题中两个截面圆的半径可以求出,但是这两个截面的位置关系有两种,即在球心的同一侧或在球心的两侧,解题的关键在于利用球心到截面的距离d与球的半径R及截面的半径r的关系构造方程计算R.【规范解答】(1)当两个截面在球心的同侧时,
如图(1)所示为球的轴截面,
由球的截面性质知,AO1∥BO2,
且O1、O2分别为两截面圆的圆心,
则OO1⊥AO1,OO2⊥BO2.
设球的半径为R.
∵π·O2B2=49π,∴O2B=7 cm.
∵π·O1A2=400π,∴O1A=20 cm.设OO1=x cm,则OO2=(x+9) cm.
在Rt△OO1A中,R2=x2+202,
在Rt△OO2B中,R2=(x+9)2+72,
∴x2+202=72+(x+9)2,解得x=15,
∴R2=x2+202=252,∴R=25 cm.
∴S球=4πR2=2 500π (cm2).
∴球的表面积为2 500π cm2.(2)当两个截面在球心的两侧时,
如图(2)所示为球的轴截面,
由球的截面性质知,O1A∥O2B,
且O1、O2分别为两截面圆的圆心,
则OO1⊥O1A,OO2⊥O2B.
设球的半径为R,
∵π·O2B2=49π,∴O2B=7 cm.
∵π·O1A2=400π,∴O1A=20 cm.设O1O=x cm,则OO2=(9-x) cm.
在Rt△OO1A中,R2=x2+400.
在Rt△OO2B中,R2=(9-x)2+49.
∴x2+400=(9-x)2+49,
解得x=-15,不合题意,舍去.
综上所述,球的表面积为2 500π cm2.【互动探究】若在本例中两个截面互相垂直,截面圆的圆心之间的距离O1O2=21 cm,试求此球的表面积.
【解题提示】两个截面互相垂直,由OO1与OO2分别垂直于两个截面可以推出OO1⊥OO2.【解析】设球的半径为R,两个截面圆的公共弦为AB,
由已知得截面圆O1的半径r1=20,截面圆O2的半径r2=7,
连接O1A,O2A,OO1,OO2,OA,
∵OO1⊥O1A,
∴OO12=OA2-O1A2=R2-202.
∵OO2⊥O2A,
∴OO22=OA2-O2A2=R2-72.∵两个截面互相垂直,OO1与OO2分别垂直于两个截面,
∴OO1⊥OO2.
∴O1O22=OO12+OO22=R2-202+R2-72=212.
解得R2=445.
所以球的表面积S=4πR2=1 780π(cm2).1.有关球的常见切接问题
(1)球切几何体时,应注意球心,如球内切于正方体,切点为正方体各个面的中心,球心为正方体的中心.
(2)球与旋转体的组合通常作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”,“接点”作出截面图.有关球的切接问题2.球与正方体的切接问题
若正方体的棱长为a,则:
(1)正方体的内切球的直径为a.如图(1);
(2)与正方体的所有棱相切的球的直径为 如图(2);
(3)正方体的外接球的直径为 如图(3). 长方体的外接球的直径等于其体对角线的长度.【例3】设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,试计算该球的表面积.
【审题指导】找出球与棱柱的相对关系,找出球的半径与三棱柱的棱长之间的关系.【规范解答】设球心为O,设正三棱柱上底面为△ABC,中
心为O′,因为三棱柱所有棱的长都为a,则可知
又由球的相关性质可知,球的半径
所以球的表面积为【变式训练】已知球的半径为R,在球内作一个内接圆柱,当圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?【解析】设圆柱底面半径为r,
高为h,O1、O2分别为上、下底
面圆的圆心,O为球心.
由题意得O为O1O2的中点,
O1O2与圆柱的底面垂直,
所以
所以所以
所以当h2=2R2即 时,S侧2取最大值4π2R4,S侧取最大值2πR2,此时
所以当圆柱底面半径为 高为 时,它的侧面积最大,侧面积的最大值是2πR2.【例】四棱锥P-ABCD中,底面ABCD是正方形,边长为a,PD=a,PD⊥平面ABCD.
(1)求四棱锥外接球的半径;
(2)在这个四棱锥中放入一个球,求球的最大半径.
【审题指导】(1)解答本题的关键是根据四棱锥的结构特征以及球面上的点到球心的距离相等分析球心的位置.
(2)与四棱锥的底面和侧面均相切时,放入的球的半径最大.【规范解答】(1)设PB的中点为F,连接BD,DF,AF,CF,
∵在Rt△PDB中,FP=FB=FD,
在Rt△PAB中FA=FP=FB,
在Rt△PBC中FP=FB=FC,
∴FP=FB=FA=FC=FD.
∴F为四棱锥外接球的球心,
则FP为外接球的半径.
∴四棱锥外接球的半径为 (2)设此球半径为R,最大的球应与四棱锥各个面都相切,设球心为S,连接SA、SB、SC、SD、SP,则把此四棱锥分为五个棱锥,它们的高均为R.
则.........【变式备选】一个球与一个正三棱柱的三个侧面和两个底
面都相切.已知这个球的体积是 求这个三棱柱的体积.
【解题提示】解答本题的关键是作出过球与正三棱柱的三个侧面的切点的截面,分析球的半径与正三棱柱的侧棱、底面边长之间的关系.【解析】过球与正三棱柱的三个侧面的切点作截面可得一个正三角形和其内切圆,如图所示.
设正三棱柱的底面边长为a,
球的半径为r,
由已知可得
所以r=2.则由三角形重心的性质得
所以
又∵正三棱柱的高h=2r=4,
∴正三棱柱的体积【典例】(12分)如图,是一个奖杯的
三视图(单位:cm),底座是正四棱台,
(1)求这个奖杯的体积(保留π);
(2)求这个奖杯的表面积(保留π).
【审题指导】解答本题可先分析该组
合体由哪些简单几何体组成及组成形
式,再分别按公式计算求和.【规范解答】由三视图可得,该奖杯的上方为直径为2r=6的球,中间为底面直径为2r′=4,高为h=16的圆柱,下面为正四棱台,棱台上底面边长为6,下底面边长为12,高h′为4. …………………………………………………………………3分
……………………………4分
V柱=πr′2h=4π×16=64π, …………………………5分 ……………………………………7分
故奖杯体积V=36π+64π+336=336+100π(cm3).
……………………………………………………………8分(2)四棱台的斜高为5,
S球=4πr2=4π×9=36π, ………………………………9分
S柱+S台=2πr′×h+S上底+S下底+S侧
=64π+36+144+180=360+64π, …………………………11分
S表=360+64π+36π=360+100π(cm2). …………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】一个空间几何体的三视图如图所示,其中主视图和左视图都是半径为1的圆,且这个几何体是球体的一部分,则这个几何体的表面积为__________.【解析】由三视图可知此几何体的表面积
=4πr2=4π×12=4π.
答案:4π1.一个球的表面积是16π,那么这个球的体积为( )
(C)16π (D)24π
【解析】选B.设球的半径为r,则4πr2=16π,
所以r=2,所以球的体积2.若球的体积与其表面积数值相等,则球的半径等于( )
(A) (B)1 (C)2 (D)3
【解析】选D.设球的半径为r,则由题意得
所以3.充满氢气的气球飞艇可以供游客旅行.现有一个球形飞艇,若要它的半径扩大为原来的4倍,那么它的体积应增大到原来的__________.
【解析】设球形飞艇原来的半径为r,则扩大后的半径为4r.
于是
答案:64倍4.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是__________.【解析】考查三视图与几何体的表面积.从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面积为S=4π×12+π×12×2+2π×1×3=12π.
答案:12π5.要把直径为5 cm的钢球放入一个正方体有盖纸盒中,请问制作出此纸盒至少要用多少纸?
【解析】用料最省时,球内切于正方体,球的直径等于正方体的棱长,所以S正方体=6×52=150(cm2).
所以制作此纸盒至少用纸150 cm2.一、选择题(每题4分,共16分)
1.在一个倒置的正三棱锥容器内放入一个钢球,钢球恰与棱锥的四个面都接触,过棱锥的一条侧棱和高作截面,正确的截面图是( )
【解析】选B.由题意知球心到两个面的距离相等且小于到侧棱的距离,故选B.2.正四面体的内切球球心到一个面的距离等于这个正四面体高的( )
【解析】选C.设正四面体的每一个表面面积都是s,高为
h,其内切球的半径为r.把球心与正四面体的四个顶点连
接,则正四面体可分成四个底面积为s,高为r的正三棱锥.
因此,正四面体的体积 所以h=4r,正四面
体的内切球球心到一个面的距离等于这个正四面体高的3.如图是一个简单组合体的直观图与三视图.下面是一个棱长为4的正方体,正上面放一个球,且球的一部分嵌入正方体中,则球的半径是( )
【解析】选B.由三视图可得,球的半径
故选B.4.过球的一条半径的中点,作垂直于该半径的平面,所得截面的面积与球的表面积之比为( )
【解析】选A.设球的半径为R,过球
的一条半径的中点,作垂直于该半径
的平面,所得圆面的半径为r,如图
所示,
在Rt△OO′A中,OA2=O′O2+O′A2,
所以
所以二、填空题(每题4分,共8分)
5.将半径为1和2的两个铅球,熔成一个大铅球,那么这个大铅球的表面积是____________.
【解析】设大铅球的半径为R,
则
所以
所以大铅球的表面积
答案: 6.圆柱形容器内盛有高度为8 cm
的水,若放入三个相同的球(球的半径与圆柱的底面
半径相同)后,水恰好淹没最上面的球(如图所示),
则球的半径是___________cm.
【解题提示】圆柱形容器底面到最上面球的顶端的容积减去圆柱内高度为8 cm的水的体积即为3个球的体积和.【解析】设球的半径为r,则底面到最上面球顶端的容积为
πr2×6r=6πr3,高度为8 cm的水的体积为8πr2,3个球的
体积和为 由题意得6πr3-8πr2=4πr3,解得
r=4.
答案:4 【方法技巧】“接”与“切”的解说
两个几何体相(内)切:一个几何体的各个面与另一个几何体的各面相切.
两个几何体相接:一个几何体的所有顶点都在另一个几何体的表面上.
解决“接、切”问题的关键是画出正确的截面,把空间“接、切”问题转化为平面“接、切”问题.三、解答题(每题8分,共16分)
7.(1)已知球的直径为6 cm,求它的表面积和体积.
(2)已知球的表面积为64π,求它的体积.
(3)已知球的体积为 求它的表面积.【解析】(1)∵直径为6 cm,
∴半径R=3 cm,
∴表面积S球=4πR2=36π(cm2),
体积
(2)∵S球=4πR2=64π,
∴R2=16,即R=4,
∴R3=125,R=5,∴S球=4πR2=100π.8.已知一底面半径为R,高为h(h>2R)的无盖圆柱形容器,装满水后倾斜45°,剩余的水恰好装满一半径也为R的球形容器,若R=3,试求圆柱形容器的高.
【解题提示】解答本题的关键是利用“补形”的方法,根据倾斜角度45°求出倒出水的体积.【解析】如图所示,倾斜
45°后倒出的水的体积为
底面半径为R,高为2R的
圆柱的体积的一半,即
V倒出水=
所以由题意知
所以h=7.【挑战能力】
(10分)设圆锥的底面半径R=2,高h=3,求:
(1)内接正方体的棱长;
(2)内切球的表面积. 【解析】(1)设圆锥内接正方体的棱长为2a.
如图所示,过正方体的相对棱作圆锥的轴截面.
由题意知AB=4. SO=3,SO1=SO-OO1=3-2a,因为△SO1B1∽△SOB,
所以 即
所以
所以圆锥内接正方体的棱长为(2)设内切球的球心为O2,半径为r,
作出圆锥的轴截面如图所示:由题意知SO2=SO-OO2=3-r,
因为△SO2A∽△SBO,
所以 即
所以
所以
(1)关键是计算球的半径,而计算半径的关键是寻找球心的位置.因此,在解题过程中要特别关注题目中所揭示的球心位置,球面上的点等信息.球的表面积和体积 (2)当球的半径增加为原来的2倍时,球的表面积增加为原来的4倍,球的体积增加为原来的8倍.
(3)注意公式的“双向”应用,也就是说当知道球的表面积或体积时,也可以求出球的半径.【例1】请用所学知识探求表面积相等的球和正方体,哪个体积更大.
【审题指导】由球和正方体的表面积相等可以得到球的半径与正方体的棱长之间的关系,将球的体积用正方体的棱长表示出来,就可以进行比较.【规范解答】设球的半径为r,正方体的棱长为a,依题意
得4πr2=6a2,所以
所以
又因为V正方体=a3,且
所以V球>V正方体.
即球的体积大于正方体的体积.【变式训练】若三个球的表面积之比为1∶2∶3,求这三个球的体积之比.
【解题提示】先由球的表面积之比求得半径之比,再求体积之比.【解析】设三个球的半径分别为R1,R2,R3,体积分别为V1,V2,V3,
∵三个球的表面积之比为1∶2∶3,
∴4πR12∶4πR22∶4πR32=R12∶R22∶R32=1∶2∶3,
∴R13∶R23∶R33
即三个球的体积之比为 有关球的截面的性质
(1)用一个平面去截一个球,
截面是圆面.
(2)球心和截面圆圆心的连线
垂直于截面.
(3)球心到截面的距离d与球
的半径R及截面的半径r满足r2=R2-d2,如图所示.球的截面问题【例2】一个球内有相距9 cm的两个平行截面,它们的面积分别为49π cm2和400π cm2,求球的表面积.
【审题指导】本题中两个截面圆的半径可以求出,但是这两个截面的位置关系有两种,即在球心的同一侧或在球心的两侧,解题的关键在于利用球心到截面的距离d与球的半径R及截面的半径r的关系构造方程计算R.【规范解答】(1)当两个截面在球心的同侧时,
如图(1)所示为球的轴截面,
由球的截面性质知,AO1∥BO2,
且O1、O2分别为两截面圆的圆心,
则OO1⊥AO1,OO2⊥BO2.
设球的半径为R.
∵π·O2B2=49π,∴O2B=7 cm.
∵π·O1A2=400π,∴O1A=20 cm.设OO1=x cm,则OO2=(x+9) cm.
在Rt△OO1A中,R2=x2+202,
在Rt△OO2B中,R2=(x+9)2+72,
∴x2+202=72+(x+9)2,解得x=15,
∴R2=x2+202=252,∴R=25 cm.
∴S球=4πR2=2 500π (cm2).
∴球的表面积为2 500π cm2.(2)当两个截面在球心的两侧时,
如图(2)所示为球的轴截面,
由球的截面性质知,O1A∥O2B,
且O1、O2分别为两截面圆的圆心,
则OO1⊥O1A,OO2⊥O2B.
设球的半径为R,
∵π·O2B2=49π,∴O2B=7 cm.
∵π·O1A2=400π,∴O1A=20 cm.设O1O=x cm,则OO2=(9-x) cm.
在Rt△OO1A中,R2=x2+400.
在Rt△OO2B中,R2=(9-x)2+49.
∴x2+400=(9-x)2+49,
解得x=-15,不合题意,舍去.
综上所述,球的表面积为2 500π cm2.【互动探究】若在本例中两个截面互相垂直,截面圆的圆心之间的距离O1O2=21 cm,试求此球的表面积.
【解题提示】两个截面互相垂直,由OO1与OO2分别垂直于两个截面可以推出OO1⊥OO2.【解析】设球的半径为R,两个截面圆的公共弦为AB,
由已知得截面圆O1的半径r1=20,截面圆O2的半径r2=7,
连接O1A,O2A,OO1,OO2,OA,
∵OO1⊥O1A,
∴OO12=OA2-O1A2=R2-202.
∵OO2⊥O2A,
∴OO22=OA2-O2A2=R2-72.∵两个截面互相垂直,OO1与OO2分别垂直于两个截面,
∴OO1⊥OO2.
∴O1O22=OO12+OO22=R2-202+R2-72=212.
解得R2=445.
所以球的表面积S=4πR2=1 780π(cm2).1.有关球的常见切接问题
(1)球切几何体时,应注意球心,如球内切于正方体,切点为正方体各个面的中心,球心为正方体的中心.
(2)球与旋转体的组合通常作它们的轴截面解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”,“接点”作出截面图.有关球的切接问题2.球与正方体的切接问题
若正方体的棱长为a,则:
(1)正方体的内切球的直径为a.如图(1);
(2)与正方体的所有棱相切的球的直径为 如图(2);
(3)正方体的外接球的直径为 如图(3). 长方体的外接球的直径等于其体对角线的长度.【例3】设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,试计算该球的表面积.
【审题指导】找出球与棱柱的相对关系,找出球的半径与三棱柱的棱长之间的关系.【规范解答】设球心为O,设正三棱柱上底面为△ABC,中
心为O′,因为三棱柱所有棱的长都为a,则可知
又由球的相关性质可知,球的半径
所以球的表面积为【变式训练】已知球的半径为R,在球内作一个内接圆柱,当圆柱底面半径与高为何值时,它的侧面积最大?侧面积的最大值是多少?【解析】设圆柱底面半径为r,
高为h,O1、O2分别为上、下底
面圆的圆心,O为球心.
由题意得O为O1O2的中点,
O1O2与圆柱的底面垂直,
所以
所以所以
所以当h2=2R2即 时,S侧2取最大值4π2R4,S侧取最大值2πR2,此时
所以当圆柱底面半径为 高为 时,它的侧面积最大,侧面积的最大值是2πR2.【例】四棱锥P-ABCD中,底面ABCD是正方形,边长为a,PD=a,PD⊥平面ABCD.
(1)求四棱锥外接球的半径;
(2)在这个四棱锥中放入一个球,求球的最大半径.
【审题指导】(1)解答本题的关键是根据四棱锥的结构特征以及球面上的点到球心的距离相等分析球心的位置.
(2)与四棱锥的底面和侧面均相切时,放入的球的半径最大.【规范解答】(1)设PB的中点为F,连接BD,DF,AF,CF,
∵在Rt△PDB中,FP=FB=FD,
在Rt△PAB中FA=FP=FB,
在Rt△PBC中FP=FB=FC,
∴FP=FB=FA=FC=FD.
∴F为四棱锥外接球的球心,
则FP为外接球的半径.
∴四棱锥外接球的半径为 (2)设此球半径为R,最大的球应与四棱锥各个面都相切,设球心为S,连接SA、SB、SC、SD、SP,则把此四棱锥分为五个棱锥,它们的高均为R.
则.........【变式备选】一个球与一个正三棱柱的三个侧面和两个底
面都相切.已知这个球的体积是 求这个三棱柱的体积.
【解题提示】解答本题的关键是作出过球与正三棱柱的三个侧面的切点的截面,分析球的半径与正三棱柱的侧棱、底面边长之间的关系.【解析】过球与正三棱柱的三个侧面的切点作截面可得一个正三角形和其内切圆,如图所示.
设正三棱柱的底面边长为a,
球的半径为r,
由已知可得
所以r=2.则由三角形重心的性质得
所以
又∵正三棱柱的高h=2r=4,
∴正三棱柱的体积【典例】(12分)如图,是一个奖杯的
三视图(单位:cm),底座是正四棱台,
(1)求这个奖杯的体积(保留π);
(2)求这个奖杯的表面积(保留π).
【审题指导】解答本题可先分析该组
合体由哪些简单几何体组成及组成形
式,再分别按公式计算求和.【规范解答】由三视图可得,该奖杯的上方为直径为2r=6的球,中间为底面直径为2r′=4,高为h=16的圆柱,下面为正四棱台,棱台上底面边长为6,下底面边长为12,高h′为4. …………………………………………………………………3分
……………………………4分
V柱=πr′2h=4π×16=64π, …………………………5分 ……………………………………7分
故奖杯体积V=36π+64π+336=336+100π(cm3).
……………………………………………………………8分(2)四棱台的斜高为5,
S球=4πr2=4π×9=36π, ………………………………9分
S柱+S台=2πr′×h+S上底+S下底+S侧
=64π+36+144+180=360+64π, …………………………11分
S表=360+64π+36π=360+100π(cm2). …………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】一个空间几何体的三视图如图所示,其中主视图和左视图都是半径为1的圆,且这个几何体是球体的一部分,则这个几何体的表面积为__________.【解析】由三视图可知此几何体的表面积
=4πr2=4π×12=4π.
答案:4π1.一个球的表面积是16π,那么这个球的体积为( )
(C)16π (D)24π
【解析】选B.设球的半径为r,则4πr2=16π,
所以r=2,所以球的体积2.若球的体积与其表面积数值相等,则球的半径等于( )
(A) (B)1 (C)2 (D)3
【解析】选D.设球的半径为r,则由题意得
所以3.充满氢气的气球飞艇可以供游客旅行.现有一个球形飞艇,若要它的半径扩大为原来的4倍,那么它的体积应增大到原来的__________.
【解析】设球形飞艇原来的半径为r,则扩大后的半径为4r.
于是
答案:64倍4.如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是__________.【解析】考查三视图与几何体的表面积.从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面积为S=4π×12+π×12×2+2π×1×3=12π.
答案:12π5.要把直径为5 cm的钢球放入一个正方体有盖纸盒中,请问制作出此纸盒至少要用多少纸?
【解析】用料最省时,球内切于正方体,球的直径等于正方体的棱长,所以S正方体=6×52=150(cm2).
所以制作此纸盒至少用纸150 cm2.一、选择题(每题4分,共16分)
1.在一个倒置的正三棱锥容器内放入一个钢球,钢球恰与棱锥的四个面都接触,过棱锥的一条侧棱和高作截面,正确的截面图是( )
【解析】选B.由题意知球心到两个面的距离相等且小于到侧棱的距离,故选B.2.正四面体的内切球球心到一个面的距离等于这个正四面体高的( )
【解析】选C.设正四面体的每一个表面面积都是s,高为
h,其内切球的半径为r.把球心与正四面体的四个顶点连
接,则正四面体可分成四个底面积为s,高为r的正三棱锥.
因此,正四面体的体积 所以h=4r,正四面
体的内切球球心到一个面的距离等于这个正四面体高的3.如图是一个简单组合体的直观图与三视图.下面是一个棱长为4的正方体,正上面放一个球,且球的一部分嵌入正方体中,则球的半径是( )
【解析】选B.由三视图可得,球的半径
故选B.4.过球的一条半径的中点,作垂直于该半径的平面,所得截面的面积与球的表面积之比为( )
【解析】选A.设球的半径为R,过球
的一条半径的中点,作垂直于该半径
的平面,所得圆面的半径为r,如图
所示,
在Rt△OO′A中,OA2=O′O2+O′A2,
所以
所以二、填空题(每题4分,共8分)
5.将半径为1和2的两个铅球,熔成一个大铅球,那么这个大铅球的表面积是____________.
【解析】设大铅球的半径为R,
则
所以
所以大铅球的表面积
答案: 6.圆柱形容器内盛有高度为8 cm
的水,若放入三个相同的球(球的半径与圆柱的底面
半径相同)后,水恰好淹没最上面的球(如图所示),
则球的半径是___________cm.
【解题提示】圆柱形容器底面到最上面球的顶端的容积减去圆柱内高度为8 cm的水的体积即为3个球的体积和.【解析】设球的半径为r,则底面到最上面球顶端的容积为
πr2×6r=6πr3,高度为8 cm的水的体积为8πr2,3个球的
体积和为 由题意得6πr3-8πr2=4πr3,解得
r=4.
答案:4 【方法技巧】“接”与“切”的解说
两个几何体相(内)切:一个几何体的各个面与另一个几何体的各面相切.
两个几何体相接:一个几何体的所有顶点都在另一个几何体的表面上.
解决“接、切”问题的关键是画出正确的截面,把空间“接、切”问题转化为平面“接、切”问题.三、解答题(每题8分,共16分)
7.(1)已知球的直径为6 cm,求它的表面积和体积.
(2)已知球的表面积为64π,求它的体积.
(3)已知球的体积为 求它的表面积.【解析】(1)∵直径为6 cm,
∴半径R=3 cm,
∴表面积S球=4πR2=36π(cm2),
体积
(2)∵S球=4πR2=64π,
∴R2=16,即R=4,
∴R3=125,R=5,∴S球=4πR2=100π.8.已知一底面半径为R,高为h(h>2R)的无盖圆柱形容器,装满水后倾斜45°,剩余的水恰好装满一半径也为R的球形容器,若R=3,试求圆柱形容器的高.
【解题提示】解答本题的关键是利用“补形”的方法,根据倾斜角度45°求出倒出水的体积.【解析】如图所示,倾斜
45°后倒出的水的体积为
底面半径为R,高为2R的
圆柱的体积的一半,即
V倒出水=
所以由题意知
所以h=7.【挑战能力】
(10分)设圆锥的底面半径R=2,高h=3,求:
(1)内接正方体的棱长;
(2)内切球的表面积. 【解析】(1)设圆锥内接正方体的棱长为2a.
如图所示,过正方体的相对棱作圆锥的轴截面.
由题意知AB=4. SO=3,SO1=SO-OO1=3-2a,因为△SO1B1∽△SOB,
所以 即
所以
所以圆锥内接正方体的棱长为(2)设内切球的球心为O2,半径为r,
作出圆锥的轴截面如图所示:由题意知SO2=SO-OO2=3-r,
因为△SO2A∽△SBO,
所以 即
所以
所以
