2.1.2 直线的方程 课件1
图片预览








文档简介
课件25张PPT。2.1.2 直线的方程1.了解直线方程的定义
2.了解直线方程的点斜式的推导过程,记住直线的点斜式和斜截式方程.
3.会求直线的点斜式和斜截式方程. 上一节我们分析了在直角坐标系内确定一条直线的
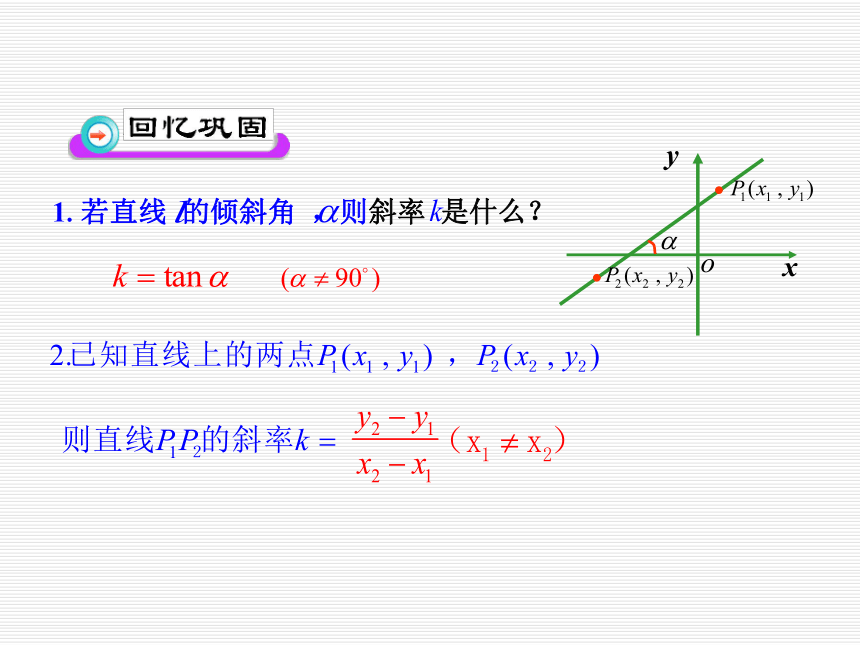
几何要素.那么我们能否用给定的条件(点 的坐标和
斜率 ),将直线上所有点的坐标( )满足的关系表示
出来呢?直线方程的定义1、直线的点斜式方程:l根据经过两点的直线斜率公式,得思考交流它的斜率是特别地1、写出下列直线的点斜式方程:2、说出下列点斜式方程所对应的直线斜率和倾斜角:直线方程的斜截式写出下列直线的斜截式方程:归纳:点斜式方程与斜截式方程的对比点斜式方程: y-y0 = k(x-x0)
几何意义:k 是直线的斜率,(x0 ,y0 )是直线上的一个点斜截式方程: y = k x +b
几何意义:k 是直线的斜率,b是直线在y轴上的截距∵直线 过 , 解:∵直线 过点 和 2、求过点(1,2)且与两坐标轴组成一等腰直角三角形的直线方程.解:∵直线与坐标轴组成一等腰直角三角形
∴k=±1直线过点(1,2)代入点斜式方程得 y–2 = x-1或 y-2=-(x-1)即 x-y+1=0或x+y-3=0点斜式,斜截式方程在直线斜率存在时才可以应用
2.了解直线方程的点斜式的推导过程,记住直线的点斜式和斜截式方程.
3.会求直线的点斜式和斜截式方程. 上一节我们分析了在直角坐标系内确定一条直线的
几何要素.那么我们能否用给定的条件(点 的坐标和
斜率 ),将直线上所有点的坐标( )满足的关系表示
出来呢?直线方程的定义1、直线的点斜式方程:l根据经过两点的直线斜率公式,得思考交流它的斜率是特别地1、写出下列直线的点斜式方程:2、说出下列点斜式方程所对应的直线斜率和倾斜角:直线方程的斜截式写出下列直线的斜截式方程:归纳:点斜式方程与斜截式方程的对比点斜式方程: y-y0 = k(x-x0)
几何意义:k 是直线的斜率,(x0 ,y0 )是直线上的一个点斜截式方程: y = k x +b
几何意义:k 是直线的斜率,b是直线在y轴上的截距∵直线 过 , 解:∵直线 过点 和 2、求过点(1,2)且与两坐标轴组成一等腰直角三角形的直线方程.解:∵直线与坐标轴组成一等腰直角三角形
∴k=±1直线过点(1,2)代入点斜式方程得 y–2 = x-1或 y-2=-(x-1)即 x-y+1=0或x+y-3=0点斜式,斜截式方程在直线斜率存在时才可以应用
