2.1.2 直线的方程 课件2
图片预览











文档简介
课件59张PPT。2.1.2 直线的方程 对直线方程的两点式和截距式的理解及认识
(1)直线的两点式体现了两点确定一条直线的思想,其形式
为 体现了数学的对称美.
(2)对于适合两点式的直线而言,这两点是任意的,但形式一定要一致,可以写成 也可以写成
但不能写成直线方程的两点式和截距式(3)在直线方程的两点式中,由于x1≠x2且y1≠y2,因此它不能表示与两坐标轴垂直的直线:
①当x1=x2,y1≠y2时,直线方程为x-x1=0,
②当y1=y2,x1≠x2时,直线方程为y-y1=0.
(4)两点式方程若变形为(y-y1)(x2-x1)=(x-x1)(y2-y1),则此方程不再受x1≠x2且y1≠y2的限制,可表示过(x1,y1), (x2,y2)的所有直线.(5)特别地,当A、B两点为直线与坐标轴的交点(非原点)时,两点式可化为截距式,所以截距式是两点式的特殊情况.
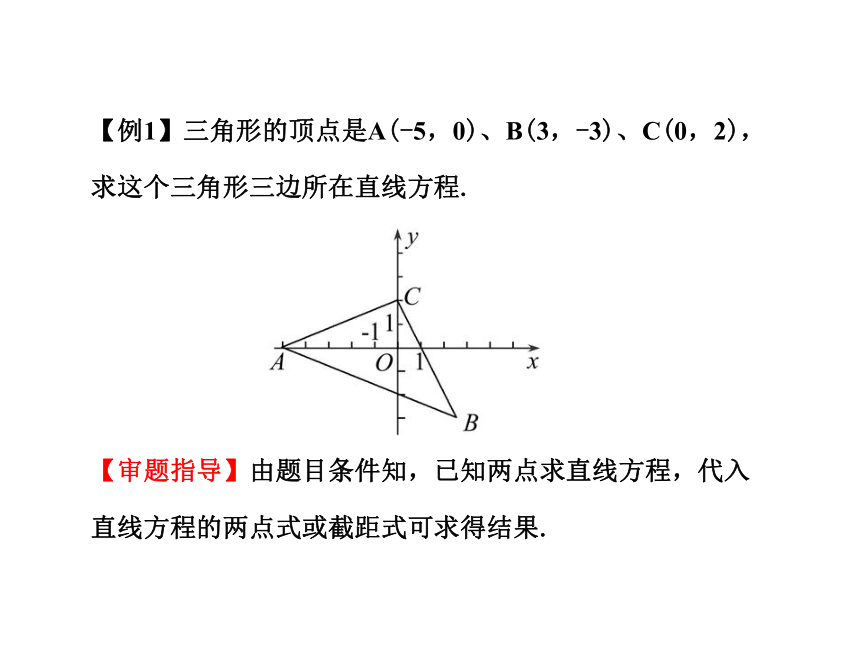
直线方程的两点式万万不能写成 的形式.【例1】三角形的顶点是A(-5,0)、B(3,-3)、C(0,2),求这个三角形三边所在直线方程.
【审题指导】由题目条件知,已知两点求直线方程,代入直线方程的两点式或截距式可求得结果.【规范解答】∵直线AB过A(-5,0)、B(3,-3)两点,
由两点式得:
整理得3x+8y+15=0.
∵直线BC过C(0,2)、B(3,-3)两点,
由两点式得:
整理得:5x+3y-6=0.
∵直线AC过A(-5,0),C(0,2)两点,
由截距式得:
整理得:2x-5y+10=0.【变式训练】已知直线l在x轴、y轴上的截距分别为-4和8,求直线l的方程,并求其斜率.
【解题提示】利用截距式写出方程,再化成斜截式求其斜率.
【解析】由直线方程的截距式可得,直线方程为
化成斜截式为y=2x+8,所以直线的斜率为2.1.直线方程形式的选择技巧
一般地, 直线方程形式的选择技巧如下:
(1)已知一点通常选择点斜式;
(2)已知斜率通常选择斜截式或点斜式;
(3)已知截距通常选择截距式;
(4)已知两点通常选择两点式.直线方程的几种形式2.直线方程的几种形式的转化 选择直线的点斜式和斜截式时,应考虑斜率不存在的情形;选择截距式时,应考虑零截距及与坐标轴平行的情形;选择两点式时,应考虑与坐标轴平行的情形.【例2】根据下列条件写出直线方程,并化为一般式方程.
(1)斜率为2,且在y轴上的截距为1;
(2)经过点P1(-2,1),P2(3,2)两点;
(3)在x轴、y轴上的截距分别为3、-5;
(4)经过点P(4,-3),且垂直于x轴.
【审题指导】根据题意灵活选择直线的方程形式:(1)斜截式,(2)两点式,(3)截距式,(4)数形结合求解.【规范解答】(1)由题意知,直线的斜截式方程为
y=2x+1,化为一般式方程为2x-y+1=0.
(2)由题意知, 直线的两点式方程为
化为一般式方程为x-5y+7=0.
(3)由题意知, 直线的截距式方程为
化为一般式方程为5x-3y-15=0.
(4)由题意知,直线方程为x=4,
化为一般式方程为x-4=0.【变式训练】已知直线x+2y-4=0,
(1)把该直线化成斜截式,并求其斜率;
(2)把该直线化成截距式,并求其在坐标轴上的截距.
【解题提示】(1)化直线为y=kx+b的形式;
(2)化直线为 的形式.【解析】(1)把该直线化成斜截式,得
所以该直线的斜率为
(2)把该直线化成截距式,得 故直线在x轴上的截
距为4,在y轴上的截距为2. 对直线方程一般式的应用的认识
(1)直线方程的一般式同二元一次方程Ax+By+C=0 (A、B不同时为零)之间是一一对应关系,因此研究直线的几何性质完全可以借助于方程的观点来研究,这实际上也是解析几何的思想所在——用方程的思想来研究几何问题.
(2)可以借助于直线方程的五种形式间的互化,求解一些定值问题、范围问题等. 一般式的综合应用【例3】设直线l的方程为(a-1)x+y-2-a=0(a∈R).若直线l不过第三象限,求a的取值范围.
【审题指导】首先把直线l化成斜截式,由直线l不过第三象限,求a的取值范围.【规范解答】把直线l化成斜截式,得
y=(1-a)x+a+2,
因为直线l不过第三象限,故该直线的斜率小于等于零,
且直线在y轴上的截距大于等于零.
即 解得a≥1.
所以a的取值范围为[1,+∞).【互动探究】若把本例中的条件“直线l不过第三象限”换成“直线l与两坐标轴围成的面积为2”,其余条件不变,求a的值.
【解题提示】求直线l在两坐标轴上的截距,利用面积为2求a的值.【解析】由题意知a≠1.令x=0,得y=a+2,
令y=0,得
所以直线l与两坐标轴围成的面积
解得a=0或a=-8.直线方程的实际应用常常与实际应用题相结合,
它涉及到直线方程的求法、函数建模思想、消元思想、二次函数最值求解等知识的综合应用,重要的是通过解析法的思想,把实际问题转化成数学问题来求解.直线方程的实际应用【例】某房地产公司要在荒地ABCDE上
划出一块长方形地面(不改变方位),
拟建造一幢八层的公寓楼,问如何设计
才能使公寓楼占地面积最大?并求出最
大面积.(精确到1 m2)
【审题指导】通过读题可发现:先应转化成代数问题,也就是建系、设点、列出关于未知量的函数式,再求解.【规范解答】建立如图所示的平面直角坐标系,则线段AB的方程为
设点P的坐标为(x,y),
则
∴公寓占地面积为
S=(100-x)(80-y)∴当x=5时,
此时点P的坐标为 故以DC、DE为邻边,
长为100-5=95(m),宽为
作长方形C′DE′P时,公寓楼的占地面积最大,
最大面积约为6 017 m2.【变式备选】如图所示,某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要购买行李票,行李票费用y(元)与行李重量x(千克)之间的关系用直线AB的方程表示.
(1)求直线AB的方程;
(2)旅客最多可免费携带多少千克行李?【解析】(1)由图知点A(60,6),B(80,10).由直线方程的两点式或斜截式可求得直线AB的方程是x-5y-30=0.
(2)由(1)知x-5y-30=0,令y=0,得x=30,即旅客最多可免费携带30千克行李.【典例】(12分)求经过点(4,-3),且在两坐标轴上的截距绝对值相等的直线方程.
【审题指导】所求直线在两坐标轴上的截距绝对值相等,故可设直线方程的截距式,需注意“零截距”的情形.【规范解答】设直线在x轴与y轴上的截距分别为a,b.
(1)当a≠0,b≠0时,设直线方程为
……………………………………………………………2分
∵直线经过点(4,-3),
…………………………………………4分
∵|a|=|b|,
∴ 或 ……………………………………6分
∴直线方程为x+y-1=0或x-y-7=0. ………………8分(2)当a=b=0时,则直线经过原点及(4,-3),
∴直线方程为3x+4y=0. ………………………………10分
综上,所求直线方程为
x+y-1=0或x-y-7=0或3x+4y=0. ………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】直线ax+by+c=0(ab≠0)在两坐标轴上的截距相等,则满足的条件是( )
(A)a≠b (B)|a|=|b|
(C)a=b且c=0 (D)a=b且c∈R
【解析】选D.当c=0时,直线过原点,显然成立.
当c≠0时,令x=0得
令y=0得 由 得a=b.
综上所述a=b且c∈R.1.下列说法正确的是( )
是表示过点(x1,y1)且斜率为k的直线
(B)在x轴和y轴上的截距分别是a、b的直线方程为
(C)y=kx+b与y轴的交点到原点的距离是b
(D)不与坐标轴平行或重合的直线方程一定可以写成两点式或斜截式【解析】选D.A不正确,因为该方程不包含点(x1,y1);B不正确,该方程不包括截距为零的直线;C不正确,截距不与距离完全相同.只有当b>0时,y=kx+b与y轴的交点到原点的距离是b.2.直线x-2y+4=0的截距式方程为( )
【解析】选D.依据截距式方程的形式得直线x-2y+4=0的截
距式方程为 选D.3.过点A(1,2),B(1,4)的直线方程为__________.
【解析】因为A、B两点的横坐标相等,故直线方程为x=1.
答案:x=14.直线Ax+By+C=0,当A>0,B<0,C>0时,此直线必经过第__________象限.
【解析】把直线Ax+By+C=0化成斜截式得
因为A>0,B<0,C>0,所以 故直线必经过
第一、二、三象限.
答案:一、二、三5.设直线l的方程为(m2-2m-3)x+(2m2+m-1)y=2m-6,根据下列条件分别求m的值.
(1)在x轴上的截距为1;
(2)斜率为1;
(3)经过定点P(-1,-1).【解析】(1)∵直线过点(1,0),∴m2-2m-3=2m-6.
解得m=3或m=1.
当m=3时,l的方程为:y=0,不合题意,当m=1时,l的方程为2x-y-2=0,符合题意,∴m=1.
(2)由斜率为1,得
解得m=-1或
当m=-1时,m2-2m-3=0且2m2+m-1=0,不合题意,
当 时,l的方程为 合题意,(3)由直线过定点P(-1,-1),
得-(m2-2m-3)-(2m2+m-1)=2m-6,
解得 或m=-2.一、选择题(每题4分,共16分)
1.直线x-y+5=0的倾斜角为( )
(A)45° (B)60°
(C)120° (D)135°
【解析】选A.∵直线x-y+5=0的斜率k=1,由tanα=1可知α=45°.2.若mx+ny+12=0在x轴和y轴上的截距分别是-3和4,则m和n 的值分别是( )
(A)4,3 (B)-4,3
(C)4,-3 (D)-4,-3
【解析】选C.由题意可知,直线过点(-3,0),(0,4).代入方程求解得m=4,n=-3.选C.3.直线ax+by-ab=0(ab≠0)在两坐标轴上的截距之和是( )
(A)a+b (B)|a|+|b|
(C)|a+b| (D)只能恒为正数
【解析】选A.把直线ax+by-ab=0(ab≠0)化成截距式得
在两坐标轴上的截距之和为a+b.4.直线l过点A(-1,-1)和B(2,5),且点C(1 005,b)也在直线l上,则b的值为( )
(A)2 008 (B)2 009
(C)2 010 (D)2 011【解析】选D.方法一:由题意可知kAB=kAC.
∴b=2 011.
方法二:由两点式得,直线l的方程为
即y=2x+1,
又点C (1 005,b)在l上,
∴b=2×1 005+1=2 011.二、填空题(每题4分,共8分)
5.若一直线经过点P(1,2),且斜率与直线y=-2x+3的斜率相等,则该直线的方程是__________.(直线方程的一般式)
【解析】∵直线y=-2x+3的斜率k=-2,又所求直线过点P(1,2),∴所求直线的方程为y=-2(x-1)+2,即2x+y-4=0.
答案:2x+y-4=06.设直线l的方程为x-y+2-a=0.若a>2,则直线l不经过第__________象限.
【解析】由x-y+2-a=0得y=x+2-a.
令x=0得y=2-a,
∵a>2,∴2-a<0,
可知l不经过第二象限.
答案:二三、解答题(每题8分,共16分)
7.求经过A(-2,3),B(4,-1)的直线的两点式方程,并把它化成点斜式、斜截式和截距式.
【解析】∵直线过A(-2,3),B(4,-1),
∴两点式方程为 即
∴点斜式方程为
斜截式方程为
截距式方程为8.已知直线l在两坐标轴上的截距之和为12,又直线l经过点(-3,4),求l的方程.
【解析】由题可设l的方程为 依题意得,
解得 或
所以所求的直线方程为
或
即4x-y+16=0或x+3y-9=0. 【方法技巧】揭秘与截距有关的问题的求解策略
1.采用截距式求直线方程时,要注意考虑“截距为零”的
情况.
2.一般地,在截距非零的情况下,可设方程为
(ab≠0).在截距为零的情况下,由于直线过原点一般可设
y=kx.3.当题目中出现“截距相等”、“截距互为相反数”或“截距间成倍数关系”等条件时,一般要先讨论截距是否为零,然后再转化成2.
4.求解有关直线与坐标轴围成的三角形的面积问题时,常把直线的方程设为截距式.【挑战能力】
(10分)已知点A(4,0),B(0,2),动点P(x,y)在线段AB上运动.
(1)求xy的最大值;
(2)在(1)中xy取最大值的前提下,是否存在过点P的直线l,使l与两坐标轴的截距相等,若存在,求l的一般式方程,若不存在,请说明理由.
【解题提示】写出直线的方程,利用变量间的等量关系建立函数关系,并求其最值.【解析】(1)由题意可知AB的方程为 (0≤x≤4, 0≤y≤2),
∴x=4-2y,
∴xy=(4-2y)·y=-2(y-1)2+2,又0≤y≤2.
∴当y=1时,xy有最大值2,此时x=2.(2)由(1)知P(2,1).
当截距为零时,设直线l:y=kx,
则1=2k,
即 也就是2y-x=0,
当截距不为零时,可设l为:
∴a=3,即l的方程为x+y-3=0.
(1)直线的两点式体现了两点确定一条直线的思想,其形式
为 体现了数学的对称美.
(2)对于适合两点式的直线而言,这两点是任意的,但形式一定要一致,可以写成 也可以写成
但不能写成直线方程的两点式和截距式(3)在直线方程的两点式中,由于x1≠x2且y1≠y2,因此它不能表示与两坐标轴垂直的直线:
①当x1=x2,y1≠y2时,直线方程为x-x1=0,
②当y1=y2,x1≠x2时,直线方程为y-y1=0.
(4)两点式方程若变形为(y-y1)(x2-x1)=(x-x1)(y2-y1),则此方程不再受x1≠x2且y1≠y2的限制,可表示过(x1,y1), (x2,y2)的所有直线.(5)特别地,当A、B两点为直线与坐标轴的交点(非原点)时,两点式可化为截距式,所以截距式是两点式的特殊情况.
直线方程的两点式万万不能写成 的形式.【例1】三角形的顶点是A(-5,0)、B(3,-3)、C(0,2),求这个三角形三边所在直线方程.
【审题指导】由题目条件知,已知两点求直线方程,代入直线方程的两点式或截距式可求得结果.【规范解答】∵直线AB过A(-5,0)、B(3,-3)两点,
由两点式得:
整理得3x+8y+15=0.
∵直线BC过C(0,2)、B(3,-3)两点,
由两点式得:
整理得:5x+3y-6=0.
∵直线AC过A(-5,0),C(0,2)两点,
由截距式得:
整理得:2x-5y+10=0.【变式训练】已知直线l在x轴、y轴上的截距分别为-4和8,求直线l的方程,并求其斜率.
【解题提示】利用截距式写出方程,再化成斜截式求其斜率.
【解析】由直线方程的截距式可得,直线方程为
化成斜截式为y=2x+8,所以直线的斜率为2.1.直线方程形式的选择技巧
一般地, 直线方程形式的选择技巧如下:
(1)已知一点通常选择点斜式;
(2)已知斜率通常选择斜截式或点斜式;
(3)已知截距通常选择截距式;
(4)已知两点通常选择两点式.直线方程的几种形式2.直线方程的几种形式的转化 选择直线的点斜式和斜截式时,应考虑斜率不存在的情形;选择截距式时,应考虑零截距及与坐标轴平行的情形;选择两点式时,应考虑与坐标轴平行的情形.【例2】根据下列条件写出直线方程,并化为一般式方程.
(1)斜率为2,且在y轴上的截距为1;
(2)经过点P1(-2,1),P2(3,2)两点;
(3)在x轴、y轴上的截距分别为3、-5;
(4)经过点P(4,-3),且垂直于x轴.
【审题指导】根据题意灵活选择直线的方程形式:(1)斜截式,(2)两点式,(3)截距式,(4)数形结合求解.【规范解答】(1)由题意知,直线的斜截式方程为
y=2x+1,化为一般式方程为2x-y+1=0.
(2)由题意知, 直线的两点式方程为
化为一般式方程为x-5y+7=0.
(3)由题意知, 直线的截距式方程为
化为一般式方程为5x-3y-15=0.
(4)由题意知,直线方程为x=4,
化为一般式方程为x-4=0.【变式训练】已知直线x+2y-4=0,
(1)把该直线化成斜截式,并求其斜率;
(2)把该直线化成截距式,并求其在坐标轴上的截距.
【解题提示】(1)化直线为y=kx+b的形式;
(2)化直线为 的形式.【解析】(1)把该直线化成斜截式,得
所以该直线的斜率为
(2)把该直线化成截距式,得 故直线在x轴上的截
距为4,在y轴上的截距为2. 对直线方程一般式的应用的认识
(1)直线方程的一般式同二元一次方程Ax+By+C=0 (A、B不同时为零)之间是一一对应关系,因此研究直线的几何性质完全可以借助于方程的观点来研究,这实际上也是解析几何的思想所在——用方程的思想来研究几何问题.
(2)可以借助于直线方程的五种形式间的互化,求解一些定值问题、范围问题等. 一般式的综合应用【例3】设直线l的方程为(a-1)x+y-2-a=0(a∈R).若直线l不过第三象限,求a的取值范围.
【审题指导】首先把直线l化成斜截式,由直线l不过第三象限,求a的取值范围.【规范解答】把直线l化成斜截式,得
y=(1-a)x+a+2,
因为直线l不过第三象限,故该直线的斜率小于等于零,
且直线在y轴上的截距大于等于零.
即 解得a≥1.
所以a的取值范围为[1,+∞).【互动探究】若把本例中的条件“直线l不过第三象限”换成“直线l与两坐标轴围成的面积为2”,其余条件不变,求a的值.
【解题提示】求直线l在两坐标轴上的截距,利用面积为2求a的值.【解析】由题意知a≠1.令x=0,得y=a+2,
令y=0,得
所以直线l与两坐标轴围成的面积
解得a=0或a=-8.直线方程的实际应用常常与实际应用题相结合,
它涉及到直线方程的求法、函数建模思想、消元思想、二次函数最值求解等知识的综合应用,重要的是通过解析法的思想,把实际问题转化成数学问题来求解.直线方程的实际应用【例】某房地产公司要在荒地ABCDE上
划出一块长方形地面(不改变方位),
拟建造一幢八层的公寓楼,问如何设计
才能使公寓楼占地面积最大?并求出最
大面积.(精确到1 m2)
【审题指导】通过读题可发现:先应转化成代数问题,也就是建系、设点、列出关于未知量的函数式,再求解.【规范解答】建立如图所示的平面直角坐标系,则线段AB的方程为
设点P的坐标为(x,y),
则
∴公寓占地面积为
S=(100-x)(80-y)∴当x=5时,
此时点P的坐标为 故以DC、DE为邻边,
长为100-5=95(m),宽为
作长方形C′DE′P时,公寓楼的占地面积最大,
最大面积约为6 017 m2.【变式备选】如图所示,某地长途汽车客运公司规定旅客可随身携带一定重量的行李,如果超过规定重量,则需要购买行李票,行李票费用y(元)与行李重量x(千克)之间的关系用直线AB的方程表示.
(1)求直线AB的方程;
(2)旅客最多可免费携带多少千克行李?【解析】(1)由图知点A(60,6),B(80,10).由直线方程的两点式或斜截式可求得直线AB的方程是x-5y-30=0.
(2)由(1)知x-5y-30=0,令y=0,得x=30,即旅客最多可免费携带30千克行李.【典例】(12分)求经过点(4,-3),且在两坐标轴上的截距绝对值相等的直线方程.
【审题指导】所求直线在两坐标轴上的截距绝对值相等,故可设直线方程的截距式,需注意“零截距”的情形.【规范解答】设直线在x轴与y轴上的截距分别为a,b.
(1)当a≠0,b≠0时,设直线方程为
……………………………………………………………2分
∵直线经过点(4,-3),
…………………………………………4分
∵|a|=|b|,
∴ 或 ……………………………………6分
∴直线方程为x+y-1=0或x-y-7=0. ………………8分(2)当a=b=0时,则直线经过原点及(4,-3),
∴直线方程为3x+4y=0. ………………………………10分
综上,所求直线方程为
x+y-1=0或x-y-7=0或3x+4y=0. ………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】直线ax+by+c=0(ab≠0)在两坐标轴上的截距相等,则满足的条件是( )
(A)a≠b (B)|a|=|b|
(C)a=b且c=0 (D)a=b且c∈R
【解析】选D.当c=0时,直线过原点,显然成立.
当c≠0时,令x=0得
令y=0得 由 得a=b.
综上所述a=b且c∈R.1.下列说法正确的是( )
是表示过点(x1,y1)且斜率为k的直线
(B)在x轴和y轴上的截距分别是a、b的直线方程为
(C)y=kx+b与y轴的交点到原点的距离是b
(D)不与坐标轴平行或重合的直线方程一定可以写成两点式或斜截式【解析】选D.A不正确,因为该方程不包含点(x1,y1);B不正确,该方程不包括截距为零的直线;C不正确,截距不与距离完全相同.只有当b>0时,y=kx+b与y轴的交点到原点的距离是b.2.直线x-2y+4=0的截距式方程为( )
【解析】选D.依据截距式方程的形式得直线x-2y+4=0的截
距式方程为 选D.3.过点A(1,2),B(1,4)的直线方程为__________.
【解析】因为A、B两点的横坐标相等,故直线方程为x=1.
答案:x=14.直线Ax+By+C=0,当A>0,B<0,C>0时,此直线必经过第__________象限.
【解析】把直线Ax+By+C=0化成斜截式得
因为A>0,B<0,C>0,所以 故直线必经过
第一、二、三象限.
答案:一、二、三5.设直线l的方程为(m2-2m-3)x+(2m2+m-1)y=2m-6,根据下列条件分别求m的值.
(1)在x轴上的截距为1;
(2)斜率为1;
(3)经过定点P(-1,-1).【解析】(1)∵直线过点(1,0),∴m2-2m-3=2m-6.
解得m=3或m=1.
当m=3时,l的方程为:y=0,不合题意,当m=1时,l的方程为2x-y-2=0,符合题意,∴m=1.
(2)由斜率为1,得
解得m=-1或
当m=-1时,m2-2m-3=0且2m2+m-1=0,不合题意,
当 时,l的方程为 合题意,(3)由直线过定点P(-1,-1),
得-(m2-2m-3)-(2m2+m-1)=2m-6,
解得 或m=-2.一、选择题(每题4分,共16分)
1.直线x-y+5=0的倾斜角为( )
(A)45° (B)60°
(C)120° (D)135°
【解析】选A.∵直线x-y+5=0的斜率k=1,由tanα=1可知α=45°.2.若mx+ny+12=0在x轴和y轴上的截距分别是-3和4,则m和n 的值分别是( )
(A)4,3 (B)-4,3
(C)4,-3 (D)-4,-3
【解析】选C.由题意可知,直线过点(-3,0),(0,4).代入方程求解得m=4,n=-3.选C.3.直线ax+by-ab=0(ab≠0)在两坐标轴上的截距之和是( )
(A)a+b (B)|a|+|b|
(C)|a+b| (D)只能恒为正数
【解析】选A.把直线ax+by-ab=0(ab≠0)化成截距式得
在两坐标轴上的截距之和为a+b.4.直线l过点A(-1,-1)和B(2,5),且点C(1 005,b)也在直线l上,则b的值为( )
(A)2 008 (B)2 009
(C)2 010 (D)2 011【解析】选D.方法一:由题意可知kAB=kAC.
∴b=2 011.
方法二:由两点式得,直线l的方程为
即y=2x+1,
又点C (1 005,b)在l上,
∴b=2×1 005+1=2 011.二、填空题(每题4分,共8分)
5.若一直线经过点P(1,2),且斜率与直线y=-2x+3的斜率相等,则该直线的方程是__________.(直线方程的一般式)
【解析】∵直线y=-2x+3的斜率k=-2,又所求直线过点P(1,2),∴所求直线的方程为y=-2(x-1)+2,即2x+y-4=0.
答案:2x+y-4=06.设直线l的方程为x-y+2-a=0.若a>2,则直线l不经过第__________象限.
【解析】由x-y+2-a=0得y=x+2-a.
令x=0得y=2-a,
∵a>2,∴2-a<0,
可知l不经过第二象限.
答案:二三、解答题(每题8分,共16分)
7.求经过A(-2,3),B(4,-1)的直线的两点式方程,并把它化成点斜式、斜截式和截距式.
【解析】∵直线过A(-2,3),B(4,-1),
∴两点式方程为 即
∴点斜式方程为
斜截式方程为
截距式方程为8.已知直线l在两坐标轴上的截距之和为12,又直线l经过点(-3,4),求l的方程.
【解析】由题可设l的方程为 依题意得,
解得 或
所以所求的直线方程为
或
即4x-y+16=0或x+3y-9=0. 【方法技巧】揭秘与截距有关的问题的求解策略
1.采用截距式求直线方程时,要注意考虑“截距为零”的
情况.
2.一般地,在截距非零的情况下,可设方程为
(ab≠0).在截距为零的情况下,由于直线过原点一般可设
y=kx.3.当题目中出现“截距相等”、“截距互为相反数”或“截距间成倍数关系”等条件时,一般要先讨论截距是否为零,然后再转化成2.
4.求解有关直线与坐标轴围成的三角形的面积问题时,常把直线的方程设为截距式.【挑战能力】
(10分)已知点A(4,0),B(0,2),动点P(x,y)在线段AB上运动.
(1)求xy的最大值;
(2)在(1)中xy取最大值的前提下,是否存在过点P的直线l,使l与两坐标轴的截距相等,若存在,求l的一般式方程,若不存在,请说明理由.
【解题提示】写出直线的方程,利用变量间的等量关系建立函数关系,并求其最值.【解析】(1)由题意可知AB的方程为 (0≤x≤4, 0≤y≤2),
∴x=4-2y,
∴xy=(4-2y)·y=-2(y-1)2+2,又0≤y≤2.
∴当y=1时,xy有最大值2,此时x=2.(2)由(1)知P(2,1).
当截距为零时,设直线l:y=kx,
则1=2k,
即 也就是2y-x=0,
当截距不为零时,可设l为:
∴a=3,即l的方程为x+y-3=0.
