2.1.3 两条直线的位置关系 课件2
文档属性
| 名称 | 2.1.3 两条直线的位置关系 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 760.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-22 14:59:54 | ||
图片预览










文档简介
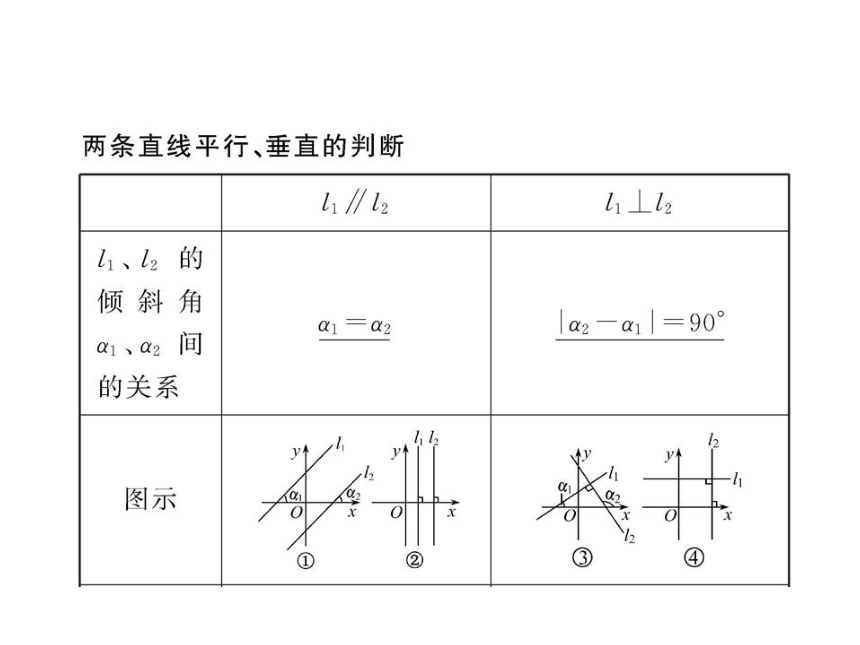
课件64张PPT。2.1.3 两条直线的位置关系 判断两直线平行、垂直的方法两条直线平行与垂直的判断 判断两直线的位置关系首先分析直线斜率是否存在.【例1】判断下列各对直线是否平行或垂直.
(1)l1:3x+4y+5=0,l2:6x+8y=10;
(2)l1:3x+5y=7,l2:5x+3y=9;
(3)l1: l2:
(4)l1:x=-2,l2:y=-2.
【审题指导】把(1)(2)化成斜截式,借助k1与k2及b1与b2的关系作出判断; 把(3)(4)画出草图,借助图形作出判断.【规范解答】(1)把直线l1、l2分别化为:
l1:
l2:
∴l1∥l2.(2)把直线l1、l2分别化为:
l1:
l2:
∴k1≠k2,且k1·k2=1≠-1.
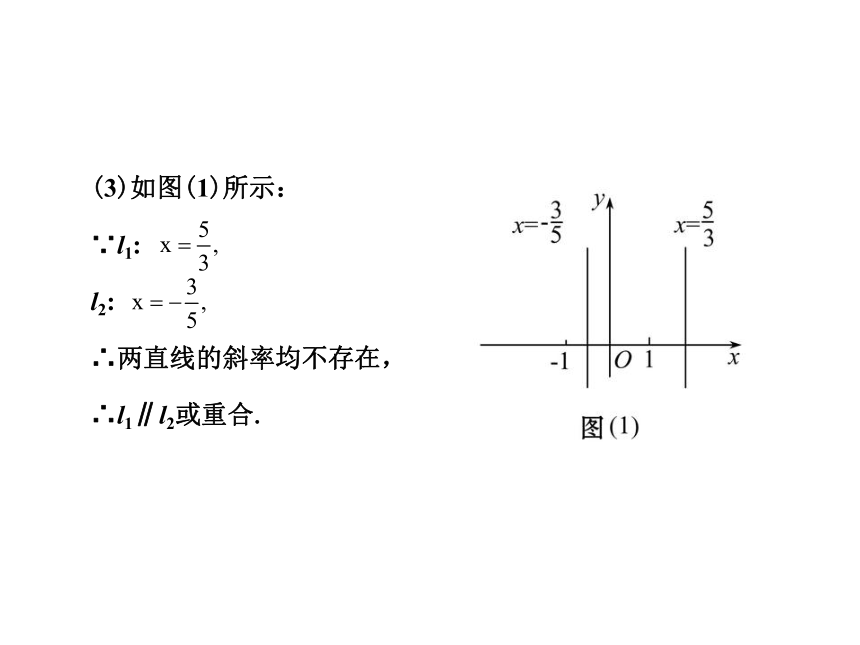
∴l1与l2既不平行也不垂直.(3)如图(1)所示:
∵l1:
l2:
∴两直线的斜率均不存在,
∴l1∥l2或重合.(4)如图(2)所示:
∵l1:x=-2,l2:y=-2,
∴l1的斜率不存在,l2的斜率为0,∴l1⊥l2.【变式训练】已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),
试判断直线BA与PQ的位置关系, 并证明你的结论.【解析】直线BA与PQ平行.证明如下:
直线BA的斜率
直线PQ的斜率
∴k1=k2.
∴直线BA与PQ可能平行也可能重合,
又直线BP的斜率
k2≠k3.
即点P(-3,1)不在直线BA上,故直线BA与PQ平行. 【误区警示】本题在求解过程中常因只验证k1=k2,而忘记检验点P(-3,1)是否在直线BA上,而盲目下结论.1.平行直线的求法:
(1)求与直线y=kx+b平行的直线方程时,根据两直线平行的条件可巧设为y=kx+m(m≠b),然后通过待定系数法,求参数m的值;
(2)求与直线Ax+By+C=0平行的直线方程时,可设方程为Ax+By+m=0(m≠C),代入已知条件求出m即可.利用两条直线平行与垂直的条件求直线方程2.垂直直线的求法:
(1)求与直线y=kx+b(k≠0)垂直的直线方程时,根据两直线
垂直的条件可巧设为 然后通过待定系数法,
求参数m的值.
(2)求与直线Ax+By+C=0(A、B不同时为零)垂直的直线时,
可巧设为Bx-Ay+m=0,然后用待定系数法,求出m.
对于斜率为零及不存在的情形要单独讨论!【例2】如图,在平行四边形OABC中,
点A(3,0),点C(1,3).
(1)求AB所在直线的方程;
(2)过点C作CD⊥AB于点D,
求CD所在直线的方程.
【审题指导】已知四边形OABC是平行四边形,可以利用平行四边形的有关性质求AB的斜率,利用两条直线垂直的条件求CD的斜率,进而求相应直线的方程.【规范解答】(1)∵点O(0,0),点C(1,3),
∴OC所在直线的斜率为
又在平行四边形OABC中,AB∥OC,
所以kAB=kOC=3,
又点A(3,0),所以AB所在直线的方程为
y=3(x-3),即3x-y-9=0.(2)在 OABC中,AB∥OC,
∵CD⊥AB,∴CD⊥OC.
∴CD所在直线的斜率为
∴CD所在直线的方程为
即x+3y-10=0.【互动探究】在本例题设不变的情况下,求点D的坐标.
【解题提示】点D在直线AB上,又在直线CD上,联立方程组求解,即可得到点D的坐标.
【解析】∵点D在直线AB上,又在直线CD上,
∴设点D的坐标为(x,y).
由题意可知
解得
所以点D的坐标为(3.7,2.1). 对用一般式表示的两直线位置关系的判定方法
设直线l1与l2的方程分别为:A1x+B1y+C1=0(A1,B1不同时为0),A2x+B2y+C2=0(A2,B2不同时为0)利用直线的平行与垂直求参数的值由此,我们得到了更一般的判定两直线平行与垂直的结论,这一结论在解决含有参数(字母)的直线平行与垂直问题时,可避开讨论斜率是否存在,从而减少了因考虑不周而造成失误的可能性.【例3】已知直线l1:ax+3y+1=0,l2:x+(a-2)y+a=0,求满足下列条件的a的值:
(1)l1∥l2; (2)l1⊥l2.
【审题指导】直线l1和l2的方程均以一般式的形式给出,要判断l1∥l2及l1⊥l2时,参数a的取值,求解思路有二:一是把方程均化成斜截式利用斜率及在y轴上截距的关系求解;二是直接利用系数A、B、C间的关系求解.【规范解答】方法一:(1)对于l1:
若l1∥l2,则 存在.
(2)若l1⊥l2,则 也存在.
解得方法二:由题可知A1=a,B1=3,C1=1;A2=1,B2=a-2,C2=a.
(1)当l1∥l2时,
有
即 解得a=3.
所以,当a=3时,l1∥l2.
(2)当l1⊥l2时,有A1A2+B1B2=a×1+3×(a-2)=0,即4a-6=0,解得
所以,当 时,l1⊥l2.【变式训练】已知直线l1的斜率为 直线l2经过点
A(3a,-2),B(0,a2+1),且l1⊥l2,求实数a的值.
【解析】∵直线l1的斜率为 且l1⊥l2,
故直线l2的斜率一定存在,且k1·kAB=-1.
又
解得a=1或a=3.
∴当a=1或a=3时,l1⊥l2. 对直线方程综合应用的认识
结合直线方程的形式及两直线平行和垂直的条件,通过方程的观点来研究生产实际问题,体现方程思想在生产实践中的应用.直线方程的综合应用【例】在路边安装路灯,路宽23 m,灯杆长2.5 m,且与灯柱成120°角,路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高h为多少米时,灯罩轴线正好通过道路路面的中线?(精确到0.01 m)
【审题指导】本题应先画出一个示意图,再通过建系,转化成有关直线问题.【规范解答】记灯柱顶端为B,灯罩顶为A,灯杆为AB,灯罩轴线与道路中线交于点C.以灯柱底端O为原点,灯柱OB为y轴,建立如图所示的直角坐标系.
点B的坐标为(0,h),点C的坐标为
(11.5,0),∵∠OBA=120°,
∴直线AB的倾斜角为30°,
则点A的坐标为
(2.5cos30°,h+2.5sin30°),即∵CA⊥BA,
由直线的点斜式方程得CA的方程为
∵灯罩轴线CA过点C(11.5,0),
解得h≈14.92(m).
故灯柱高h约为14.92 m.【变式备选】过点A(1,-1)向直线l作垂线,垂足为B(-3,1).求直线l与坐标轴围成的三角形的面积. 【解析】由题知AB所在的直线的斜率为
设直线l的斜率为k,
∴直线l的方程为:y-1=2(x+3),即2x-y+7=0.
∴直线l与坐标轴的交点坐标为
∴直线l与坐标轴围成的三角形的面积【典例】(12分)已知A(0,3)、B(-1,0)、C(3,0),求D点的坐标,使四边形ABCD为直角梯形(A、B、C、D按逆时针方向排列).
【审题指导】解答本题可先对直角梯形中哪个角为直角进行讨论,然后借助于平行、垂直的关系列方程组求D点的坐标.【规范解答】设所求点D的坐标为
(x,y),如图所示.
由于kAB=3,kBC=0,
∴kAB·kBC=0≠-1,
即AB与BC不垂直,故AB、BC都不可作为直角梯形的直角腰. …………………………………………………………2分①若CD是直角梯形的直角腰,则BC⊥CD,AD⊥CD.
∵kBC=0,
∴CD的斜率不存在,从而有x=3.
又kAD=kBC,
此时AB与CD不平行.
故所求点D的坐标为(3,3). ……………………………7分②若AD是直角梯形的直角腰,则AD⊥AB,AD⊥CD.
又由于AD⊥AB,
①
又AB∥CD, ②
……………………………………………………………9分解①②可得 此时AD与BC不平行,
即所求D点的坐标为 ……………………11分
综上可知,使四边形ABCD为直角梯形的点D的坐标为(3,3)或 …………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】已知四边形ABCD的顶点坐标
试判断四边形ABCD的形状.【解析】AB边所在直线的斜率:
CD边所在直线的斜率:
BC边所在直线的斜率:
DA边所在直线的斜率:∴kAB=kCD,kBC=kDA.
∴AB∥CD,BC∥DA.
∴四边形ABCD为平行四边形.
又
所以AB⊥BC.又
故kAC·kBD=0≠-1,∴AC与BD不垂直.
∴四边形ABCD为矩形.·1.下列各组中的两条直线平行的有( )
(1)2x+y-11=0 x+3y-18=0
(2)2x-3y-4=0 4x-6y-8=0
(3)3x-4y-7=0 12x-16y-7=0
(A)0组 (B)1组 (C)2组 (D)3组
【解析】选B.(1)两直线的斜率不相等故不平行;(2)两直线重合;(3)两直线的斜率相等,且在y轴上的截距不相等,故平行.2.直线l过点(-1,2)且与直线2x-3y+4=0垂直,则l的方程是
( )
(A)3x+2y-1=0 (B)3x+2y+7=0
(C)2x-3y+5=0 (D)2x-3y+8=0
【解析】选A.可得直线l的斜率为
∴l的方程为
即3x+2y-1=0,选A.3.若直线l1:x+y-3=0与l2:(a-3)x+y+2=0互相平行,则实数a的值是__________.
【解析】直线l1可化为:y=-x+3,直线l2可化为:
y=(3-a)x-2.由l1∥l2得3-a=-1,解得a=4.
答案:44.已知经过两点(3,2)和(m,n)的直线l.
(1)若l与x轴平行,则m,n的取值情况是__________;
(2)若l与x轴垂直,则m,n的取值情况是__________.【解析】(1)∵l与x轴平行,由图①可知m∈R且m≠3,n=2.
(2)∵l与x轴垂直,由图②可知m=3,n∈R且n≠2.
答案:(1)m∈R且m≠3,n=2 (2)m=3,n∈R且n≠25.已知P(2,1),直线l:x-y+4=0.
(1)求过点P与直线l平行的直线方程;
(2)求过点P与直线l垂直的直线方程.
【解析】(1)设过点P与直线l平行的直线方程为x-y+m=0.
由题意可知2-1+m=0,解得m=-1.
所以过点P与直线l平行的直线方程为x-y-1=0.
(2)设过点P与直线l垂直的直线方程为x+y+n=0.
由题意可知2+1+n=0,解得n=-3.
所以过点P与直线l垂直的直线方程为x+y-3=0.一、选择题(每题4分,共16分)
1.过点(1,0)且与直线x-2y-2=0平行的直线方程是( )
(A)x-2y-1=0 (B)x-2y+1=0
(C)2x+y-2=0 (D)x+2y-1=0
【解题提示】可设所求直线方程为x-2y+c=0,代入已知点的坐标得c的值,进而得直线方程.
【解析】选A.设直线方程为x-2y+c=0,又过(1,0),故
c=-1,所求方程为x-2y-1=0.2.经过(m,3)与(2,m)的直线l与斜率为-4的直线相互垂直,则m的值为( )
【解析】选D.由题意可知
解得3.已知点P(0,-1),点Q在直线x-y+1=0上,若直线PQ垂直于直线x+2y-5=0,则点Q的坐标是( )
(A)(-2,1) (B)(2,1)
(C)(2,3) (D)(-2,-1)
【解析】选C.设Q(x,y),由题意可知kPQ=2,又
由 得x=2,∴Q(2,3).4.已知A(-1,3),B(3,1),点C在坐标轴上,若∠ACB= 90°,则这样的点C的个数为( )
(A)1 (B)2 (C)3 (D)4
【解题提示】由于题目只告诉点C在坐标轴上,没明确是x轴还是y轴,因此求解时应分类讨论.【解析】选C.①设C(x,0),则由kAC·kBC=-1,得
∴x=0或x=2,即C为(0,0)或(2,0).
②设C(0,y),则由kAC·kBC=-1,
得
∴y=0或y=4.即C为(0,0)或(0,4).
故这样的点C有3个.故选C.·· 【方法技巧】分类讨论的依据
在解题中同学们常常遇到含参数的问题,如果参数的变化对题目的结果产生了影响,我们一般会联想到解题时可能会用到分类讨论的思想;但有些题目不直接给出参数,而是通过图形的不确定性引发分类讨论,如本题因点C的不明确落在哪个轴上而引发讨论;另还有角的不明确性,方程的不明确性等等.学习中要多多注意总结.二、填空题(每题4分,共8分)
5. 已知直线mx+4y-2=0与2x-5y+n=0垂直,垂足为(1,p),则m-n+p=__________.
【解析】由mx+4y-2=0与2x-5y+n=0垂直,知
∴m=10.
又垂足为(1,p),∴
解得 ∴m-n+p=10+12-2=20.
答案:206.如果直线ax+2y+2=0与直线3x-y-2=0平行,则a=__________.
【解析】∵直线3x-y-2=0的斜率为3,
∴直线ax+2y+2=0的斜率为
∴a=-6.
答案:-6三、解答题(每题8分,共16分)
7.已知三角形的三个顶点坐标为A(2,4),B(1,-2),
C(-2,3),求BC边上的高AD所在的直线方程.
【解析】直线BC的斜率为
∵AD⊥BC,
根据点斜式得BC边上的高AD所在的直线方程为
即3x-5y+14=0.8.已知点M(2,2),N(5,-2),点 P在x轴上,分别求满足下列条件的P的坐标.
(1)∠MOP=∠OPN(O为坐标原点);
(2)∠MPN是直角.
【解题提示】 (1)由∠MOP=∠OPN可知直线MO∥PN;
(2)由∠MPN是直角知MP⊥NP.【解析】设P(x,0).
(1)∵∠MOP=∠OPN,∴MO∥PN.
∴kOM=kNP.
又
解得x=7,即P(7,0).(2)∵∠MPN=90°,∴MP⊥NP.
∴kMP·kNP=-1.
解得x=1或x=6.
∴P(1,0)或(6,0).【挑战能力】
(10分)△ABC的顶点A(5,-1)、B(1,1)、C(2,m),若△ABC为直角三角形,求m的值.【解析】若∠A为直角,则AC⊥AB,
所以kAC·kAB=-1,即
得m=-7;
若∠B为直角,则AB⊥BC,所以kAB·kBC=-1,
即 得m=3;
若∠C为直角,则AC⊥BC,所以kAC·kBC=-1,
即 得m=±2.
综上可知,m=-7或m=3或m=±2.···
(1)l1:3x+4y+5=0,l2:6x+8y=10;
(2)l1:3x+5y=7,l2:5x+3y=9;
(3)l1: l2:
(4)l1:x=-2,l2:y=-2.
【审题指导】把(1)(2)化成斜截式,借助k1与k2及b1与b2的关系作出判断; 把(3)(4)画出草图,借助图形作出判断.【规范解答】(1)把直线l1、l2分别化为:
l1:
l2:
∴l1∥l2.(2)把直线l1、l2分别化为:
l1:
l2:
∴k1≠k2,且k1·k2=1≠-1.
∴l1与l2既不平行也不垂直.(3)如图(1)所示:
∵l1:
l2:
∴两直线的斜率均不存在,
∴l1∥l2或重合.(4)如图(2)所示:
∵l1:x=-2,l2:y=-2,
∴l1的斜率不存在,l2的斜率为0,∴l1⊥l2.【变式训练】已知A(2,3),B(-4,0),P(-3,1),Q(-1,2),
试判断直线BA与PQ的位置关系, 并证明你的结论.【解析】直线BA与PQ平行.证明如下:
直线BA的斜率
直线PQ的斜率
∴k1=k2.
∴直线BA与PQ可能平行也可能重合,
又直线BP的斜率
k2≠k3.
即点P(-3,1)不在直线BA上,故直线BA与PQ平行. 【误区警示】本题在求解过程中常因只验证k1=k2,而忘记检验点P(-3,1)是否在直线BA上,而盲目下结论.1.平行直线的求法:
(1)求与直线y=kx+b平行的直线方程时,根据两直线平行的条件可巧设为y=kx+m(m≠b),然后通过待定系数法,求参数m的值;
(2)求与直线Ax+By+C=0平行的直线方程时,可设方程为Ax+By+m=0(m≠C),代入已知条件求出m即可.利用两条直线平行与垂直的条件求直线方程2.垂直直线的求法:
(1)求与直线y=kx+b(k≠0)垂直的直线方程时,根据两直线
垂直的条件可巧设为 然后通过待定系数法,
求参数m的值.
(2)求与直线Ax+By+C=0(A、B不同时为零)垂直的直线时,
可巧设为Bx-Ay+m=0,然后用待定系数法,求出m.
对于斜率为零及不存在的情形要单独讨论!【例2】如图,在平行四边形OABC中,
点A(3,0),点C(1,3).
(1)求AB所在直线的方程;
(2)过点C作CD⊥AB于点D,
求CD所在直线的方程.
【审题指导】已知四边形OABC是平行四边形,可以利用平行四边形的有关性质求AB的斜率,利用两条直线垂直的条件求CD的斜率,进而求相应直线的方程.【规范解答】(1)∵点O(0,0),点C(1,3),
∴OC所在直线的斜率为
又在平行四边形OABC中,AB∥OC,
所以kAB=kOC=3,
又点A(3,0),所以AB所在直线的方程为
y=3(x-3),即3x-y-9=0.(2)在 OABC中,AB∥OC,
∵CD⊥AB,∴CD⊥OC.
∴CD所在直线的斜率为
∴CD所在直线的方程为
即x+3y-10=0.【互动探究】在本例题设不变的情况下,求点D的坐标.
【解题提示】点D在直线AB上,又在直线CD上,联立方程组求解,即可得到点D的坐标.
【解析】∵点D在直线AB上,又在直线CD上,
∴设点D的坐标为(x,y).
由题意可知
解得
所以点D的坐标为(3.7,2.1). 对用一般式表示的两直线位置关系的判定方法
设直线l1与l2的方程分别为:A1x+B1y+C1=0(A1,B1不同时为0),A2x+B2y+C2=0(A2,B2不同时为0)利用直线的平行与垂直求参数的值由此,我们得到了更一般的判定两直线平行与垂直的结论,这一结论在解决含有参数(字母)的直线平行与垂直问题时,可避开讨论斜率是否存在,从而减少了因考虑不周而造成失误的可能性.【例3】已知直线l1:ax+3y+1=0,l2:x+(a-2)y+a=0,求满足下列条件的a的值:
(1)l1∥l2; (2)l1⊥l2.
【审题指导】直线l1和l2的方程均以一般式的形式给出,要判断l1∥l2及l1⊥l2时,参数a的取值,求解思路有二:一是把方程均化成斜截式利用斜率及在y轴上截距的关系求解;二是直接利用系数A、B、C间的关系求解.【规范解答】方法一:(1)对于l1:
若l1∥l2,则 存在.
(2)若l1⊥l2,则 也存在.
解得方法二:由题可知A1=a,B1=3,C1=1;A2=1,B2=a-2,C2=a.
(1)当l1∥l2时,
有
即 解得a=3.
所以,当a=3时,l1∥l2.
(2)当l1⊥l2时,有A1A2+B1B2=a×1+3×(a-2)=0,即4a-6=0,解得
所以,当 时,l1⊥l2.【变式训练】已知直线l1的斜率为 直线l2经过点
A(3a,-2),B(0,a2+1),且l1⊥l2,求实数a的值.
【解析】∵直线l1的斜率为 且l1⊥l2,
故直线l2的斜率一定存在,且k1·kAB=-1.
又
解得a=1或a=3.
∴当a=1或a=3时,l1⊥l2. 对直线方程综合应用的认识
结合直线方程的形式及两直线平行和垂直的条件,通过方程的观点来研究生产实际问题,体现方程思想在生产实践中的应用.直线方程的综合应用【例】在路边安装路灯,路宽23 m,灯杆长2.5 m,且与灯柱成120°角,路灯采用锥形灯罩,灯罩轴线与灯杆垂直.当灯柱高h为多少米时,灯罩轴线正好通过道路路面的中线?(精确到0.01 m)
【审题指导】本题应先画出一个示意图,再通过建系,转化成有关直线问题.【规范解答】记灯柱顶端为B,灯罩顶为A,灯杆为AB,灯罩轴线与道路中线交于点C.以灯柱底端O为原点,灯柱OB为y轴,建立如图所示的直角坐标系.
点B的坐标为(0,h),点C的坐标为
(11.5,0),∵∠OBA=120°,
∴直线AB的倾斜角为30°,
则点A的坐标为
(2.5cos30°,h+2.5sin30°),即∵CA⊥BA,
由直线的点斜式方程得CA的方程为
∵灯罩轴线CA过点C(11.5,0),
解得h≈14.92(m).
故灯柱高h约为14.92 m.【变式备选】过点A(1,-1)向直线l作垂线,垂足为B(-3,1).求直线l与坐标轴围成的三角形的面积. 【解析】由题知AB所在的直线的斜率为
设直线l的斜率为k,
∴直线l的方程为:y-1=2(x+3),即2x-y+7=0.
∴直线l与坐标轴的交点坐标为
∴直线l与坐标轴围成的三角形的面积【典例】(12分)已知A(0,3)、B(-1,0)、C(3,0),求D点的坐标,使四边形ABCD为直角梯形(A、B、C、D按逆时针方向排列).
【审题指导】解答本题可先对直角梯形中哪个角为直角进行讨论,然后借助于平行、垂直的关系列方程组求D点的坐标.【规范解答】设所求点D的坐标为
(x,y),如图所示.
由于kAB=3,kBC=0,
∴kAB·kBC=0≠-1,
即AB与BC不垂直,故AB、BC都不可作为直角梯形的直角腰. …………………………………………………………2分①若CD是直角梯形的直角腰,则BC⊥CD,AD⊥CD.
∵kBC=0,
∴CD的斜率不存在,从而有x=3.
又kAD=kBC,
此时AB与CD不平行.
故所求点D的坐标为(3,3). ……………………………7分②若AD是直角梯形的直角腰,则AD⊥AB,AD⊥CD.
又由于AD⊥AB,
①
又AB∥CD, ②
……………………………………………………………9分解①②可得 此时AD与BC不平行,
即所求D点的坐标为 ……………………11分
综上可知,使四边形ABCD为直角梯形的点D的坐标为(3,3)或 …………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】已知四边形ABCD的顶点坐标
试判断四边形ABCD的形状.【解析】AB边所在直线的斜率:
CD边所在直线的斜率:
BC边所在直线的斜率:
DA边所在直线的斜率:∴kAB=kCD,kBC=kDA.
∴AB∥CD,BC∥DA.
∴四边形ABCD为平行四边形.
又
所以AB⊥BC.又
故kAC·kBD=0≠-1,∴AC与BD不垂直.
∴四边形ABCD为矩形.·1.下列各组中的两条直线平行的有( )
(1)2x+y-11=0 x+3y-18=0
(2)2x-3y-4=0 4x-6y-8=0
(3)3x-4y-7=0 12x-16y-7=0
(A)0组 (B)1组 (C)2组 (D)3组
【解析】选B.(1)两直线的斜率不相等故不平行;(2)两直线重合;(3)两直线的斜率相等,且在y轴上的截距不相等,故平行.2.直线l过点(-1,2)且与直线2x-3y+4=0垂直,则l的方程是
( )
(A)3x+2y-1=0 (B)3x+2y+7=0
(C)2x-3y+5=0 (D)2x-3y+8=0
【解析】选A.可得直线l的斜率为
∴l的方程为
即3x+2y-1=0,选A.3.若直线l1:x+y-3=0与l2:(a-3)x+y+2=0互相平行,则实数a的值是__________.
【解析】直线l1可化为:y=-x+3,直线l2可化为:
y=(3-a)x-2.由l1∥l2得3-a=-1,解得a=4.
答案:44.已知经过两点(3,2)和(m,n)的直线l.
(1)若l与x轴平行,则m,n的取值情况是__________;
(2)若l与x轴垂直,则m,n的取值情况是__________.【解析】(1)∵l与x轴平行,由图①可知m∈R且m≠3,n=2.
(2)∵l与x轴垂直,由图②可知m=3,n∈R且n≠2.
答案:(1)m∈R且m≠3,n=2 (2)m=3,n∈R且n≠25.已知P(2,1),直线l:x-y+4=0.
(1)求过点P与直线l平行的直线方程;
(2)求过点P与直线l垂直的直线方程.
【解析】(1)设过点P与直线l平行的直线方程为x-y+m=0.
由题意可知2-1+m=0,解得m=-1.
所以过点P与直线l平行的直线方程为x-y-1=0.
(2)设过点P与直线l垂直的直线方程为x+y+n=0.
由题意可知2+1+n=0,解得n=-3.
所以过点P与直线l垂直的直线方程为x+y-3=0.一、选择题(每题4分,共16分)
1.过点(1,0)且与直线x-2y-2=0平行的直线方程是( )
(A)x-2y-1=0 (B)x-2y+1=0
(C)2x+y-2=0 (D)x+2y-1=0
【解题提示】可设所求直线方程为x-2y+c=0,代入已知点的坐标得c的值,进而得直线方程.
【解析】选A.设直线方程为x-2y+c=0,又过(1,0),故
c=-1,所求方程为x-2y-1=0.2.经过(m,3)与(2,m)的直线l与斜率为-4的直线相互垂直,则m的值为( )
【解析】选D.由题意可知
解得3.已知点P(0,-1),点Q在直线x-y+1=0上,若直线PQ垂直于直线x+2y-5=0,则点Q的坐标是( )
(A)(-2,1) (B)(2,1)
(C)(2,3) (D)(-2,-1)
【解析】选C.设Q(x,y),由题意可知kPQ=2,又
由 得x=2,∴Q(2,3).4.已知A(-1,3),B(3,1),点C在坐标轴上,若∠ACB= 90°,则这样的点C的个数为( )
(A)1 (B)2 (C)3 (D)4
【解题提示】由于题目只告诉点C在坐标轴上,没明确是x轴还是y轴,因此求解时应分类讨论.【解析】选C.①设C(x,0),则由kAC·kBC=-1,得
∴x=0或x=2,即C为(0,0)或(2,0).
②设C(0,y),则由kAC·kBC=-1,
得
∴y=0或y=4.即C为(0,0)或(0,4).
故这样的点C有3个.故选C.·· 【方法技巧】分类讨论的依据
在解题中同学们常常遇到含参数的问题,如果参数的变化对题目的结果产生了影响,我们一般会联想到解题时可能会用到分类讨论的思想;但有些题目不直接给出参数,而是通过图形的不确定性引发分类讨论,如本题因点C的不明确落在哪个轴上而引发讨论;另还有角的不明确性,方程的不明确性等等.学习中要多多注意总结.二、填空题(每题4分,共8分)
5. 已知直线mx+4y-2=0与2x-5y+n=0垂直,垂足为(1,p),则m-n+p=__________.
【解析】由mx+4y-2=0与2x-5y+n=0垂直,知
∴m=10.
又垂足为(1,p),∴
解得 ∴m-n+p=10+12-2=20.
答案:206.如果直线ax+2y+2=0与直线3x-y-2=0平行,则a=__________.
【解析】∵直线3x-y-2=0的斜率为3,
∴直线ax+2y+2=0的斜率为
∴a=-6.
答案:-6三、解答题(每题8分,共16分)
7.已知三角形的三个顶点坐标为A(2,4),B(1,-2),
C(-2,3),求BC边上的高AD所在的直线方程.
【解析】直线BC的斜率为
∵AD⊥BC,
根据点斜式得BC边上的高AD所在的直线方程为
即3x-5y+14=0.8.已知点M(2,2),N(5,-2),点 P在x轴上,分别求满足下列条件的P的坐标.
(1)∠MOP=∠OPN(O为坐标原点);
(2)∠MPN是直角.
【解题提示】 (1)由∠MOP=∠OPN可知直线MO∥PN;
(2)由∠MPN是直角知MP⊥NP.【解析】设P(x,0).
(1)∵∠MOP=∠OPN,∴MO∥PN.
∴kOM=kNP.
又
解得x=7,即P(7,0).(2)∵∠MPN=90°,∴MP⊥NP.
∴kMP·kNP=-1.
解得x=1或x=6.
∴P(1,0)或(6,0).【挑战能力】
(10分)△ABC的顶点A(5,-1)、B(1,1)、C(2,m),若△ABC为直角三角形,求m的值.【解析】若∠A为直角,则AC⊥AB,
所以kAC·kAB=-1,即
得m=-7;
若∠B为直角,则AB⊥BC,所以kAB·kBC=-1,
即 得m=3;
若∠C为直角,则AC⊥BC,所以kAC·kBC=-1,
即 得m=±2.
综上可知,m=-7或m=3或m=±2.···
