2.1.4 两条直线的交点 课件2
图片预览










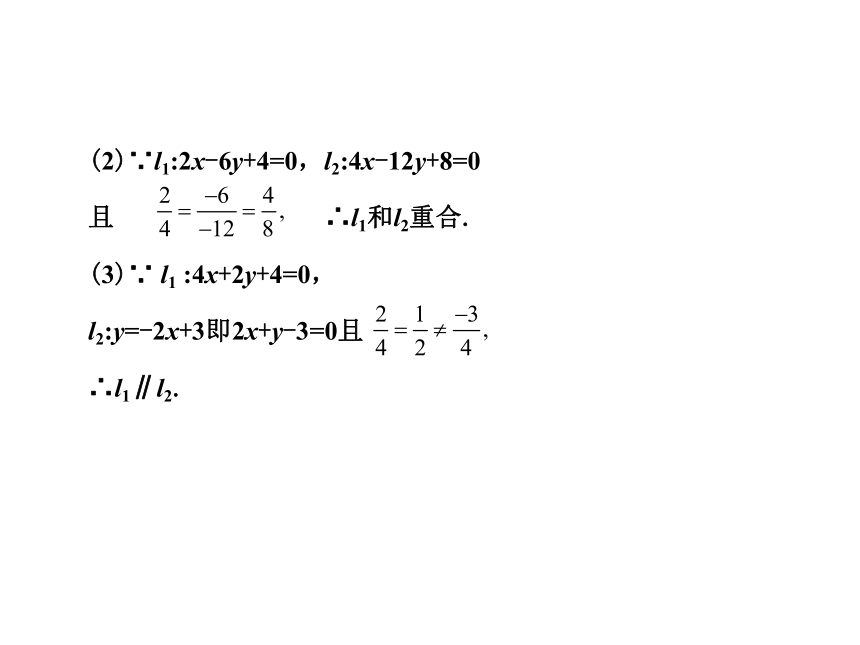
文档简介
课件62张PPT。2.1.4 两条直线的交点1.对两直线位置关系的进一步理解
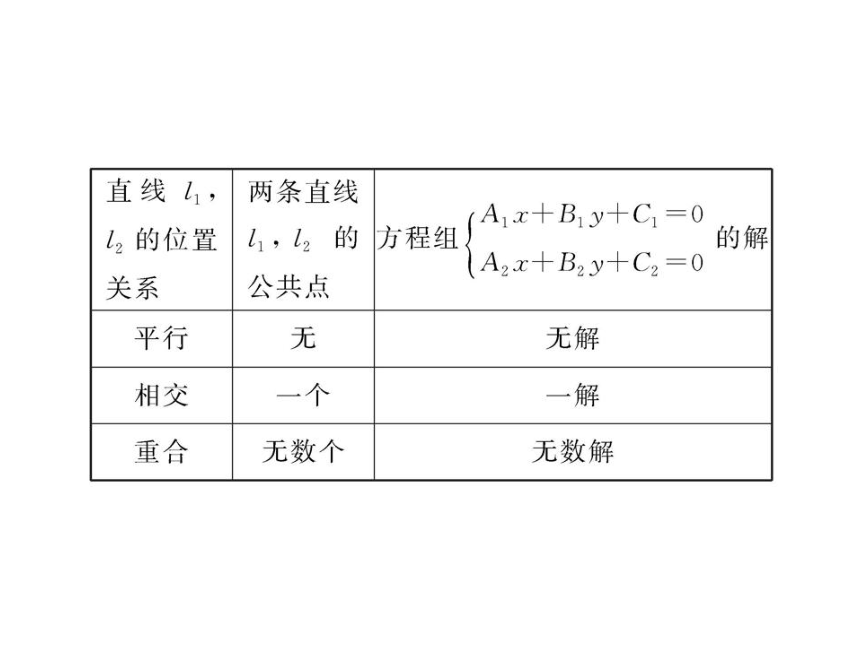
研究两条直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0的位置关系(相交、重合、平行)可以转化为两条直线方程所得的方程
组 的解的个数问题.具体情况如下:两直线位置关系的判断 2.两条直线相交的判定方法:
若只判断两直线是否相交采用方法(1)较方便,若要求交点坐标则采用方法(2).【例1】分别判断下列直线的位置关系,若相交,求出它们的交点:
(1)l1:2x-y=7,l2:3x+2y-7=0;
(2)l1:2x-6y+4=0,l2:4x-12y+8=0;
(3)l1:4x+2y+4=0,l2:y=-2x+3.
【审题指导】思路一:利用方程组的观点判断直线的位置关系,并求交点;思路二:利用斜率的关系判断直线的位置关系,若相交再利用方程组求交点.【规范解答】方法一:(1)∵
的解为
∴直线l1与l2相交,交点坐标为(3,-1).
(2)∵ 有无数组解,
∴ l1和l2重合.
(3)∵ 无解,∴l1∥l2.方法二:(1)∵l1:2x-y=7,l2:3x+2y-7=0的斜率不相等,
故两直线相交.由
解得
∴直线l1与l2的交点坐标为(3,-1).(2)∵l1:2x-6y+4=0,l2:4x-12y+8=0
且 ∴l1和l2重合.
(3)∵ l1 :4x+2y+4=0,
l2:y=-2x+3即2x+y-3=0且
∴l1∥l2.【互动探究】把本题(1)“l1:2x-y=7”换成“l1:ax-y=7”求相应问题.
【解题提示】解方程组,按方程是否有解对参数a进行讨论.【解析】由 得(3+2a)x=21.
当 时,原方程组无解,∴l1∥l2.
当 时,原方程组有且只有一解
∴直线l1与l2相交,交点坐标为 利用两直线的位置关系求参数值的方法:
已知直线的一般式且明确了直线间的关系求参数的值(或范围)时,其求解思路为:利用两直线的位置关系求参数的值 上述一般式给出的方程,其平行和重合的条件务必分清.【例2】已知两条直线l1:x+my+6=0, l2:(m-2)x+3y+2m=0问:当m为何值时,l1与l2
(1)平行; (2)垂直; (3)重合.
【审题指导】方程以一般式的形式给出,直接应用两直线平行、垂直、重合的等价条件求解.【规范解答】(1)∵l1∥l2
∴3-m(m-2)=0.
即m2-2m-3=0.∴m=-1或m=3.
经检验当m=3时两直线重合,故m=3舍去.
∴m=-1.
(2)∵l1⊥l2,∴1×(m-2)+3m=0,
(3)由(1)可知当m=3时两直线重合.【变式训练】已知直线l1:(k-3)x+(4-k)y+1=0,与
l2:2(k-3)x-2y+3=0平行,则k的值为( )
(A)1或3 (B)1或5
(C)3或5 (D)1或2
【解析】选C.方法一:当k=3时,两直线平行,当k≠3时,
由两直线平行,斜率相等,得: 解得:k=5.
方法二:由-2(k-3)-2(k-3)(4-k)=0得k=3或k=5.
经验证当k=3或k=5时均合题意. 线共点问题的求解方法
(1)方程组法:选择两条较易求解交点的直线方程联立,求出相应交点的坐标P(x0,y0),然后把P(x0,y0)代入另一条直线方程,利用方程的思想求解参数.过交点的直线系(2)直线系法:①经过两直线l1:A1x+B1y+C1=0(A12+B12≠0)和l2:A2x+B2y+C2=0(A22+B22≠0)交点的直线系为m(A1x+B1y+C1) +n(A2x+B2y+C2)=0(其中m,n为参数,m2+n2≠ 0).
当m=1,n=0时,方程即为l1的方程;
当m=0,n=1时,方程即为l2的方程;②上面的直线系可改写成(A1x+B1y+C1)+λ(A2x+B2y+C2)=0 (其中λ∈R).但是此方程中不包括直线l2,这个参数方程形式在解题中较为常用.
比较两种方法可知,如果多条直线交于一点,采用过交点的直线系求解相交问题较简单.③直线系方程(A1x+B1y+C1)+λ(A2x+B2y+C2)=0中,由①、②
可知,此直线系方程恒过定点
④方程y-y0=k(x-x0),由点斜式知,它恒过定点(x0,y0),也
可以化为(y-y0)-k(x-x0)=0,
过定点 即(x0,y0). (1)与直线Ax+By+C=0垂直的直线的方程可设为Bx-Ay+m=0,其中m待定.
(2)与直线Ax+By+C=0平行的直线的方程可设为Ax+By+m=0,其中m待定.【例3】已知直线l1:3x-y-1=0,l2:x+y-3=0,求:
(1)直线l1与l2的交点P的坐标;
(2)过点P且与l1垂直的直线方程.
【审题指导】由于本题l1,l2的方程已知,可利用解方程组的方法求出交点P,进而再求出所求的直线方程.【规范解答】(1)解方程组 得
所以直线l1与l2的交点P的坐标为(1,2).
(2)方法一:直线l1的斜率为3,故过点P且与l1垂直的直线方程
为 即为x+3y-7=0.
方法二:由题意可设所求直线的方程为
3x-y-1+λ(x+y-3)=0,整理得
(3+λ)x+(λ-1)y-1-3λ=0,
又∵该直线与l1垂直,故3×(3+λ)+(-1)×(λ-1)=0,
解得λ=-5.即所求直线的方程为x+3y-7=0.【变式训练】(1)已知直线l经过两条直线2x-3y-3=0和x+y+2=0的交点,且与直线3x+y-1=0平行,求直线l的方程.
(2)已知直线l经过两条直线2x-2y+10=0和3x+4y-2=0的交点,且垂直于直线3x-2y+4=0,求直线l的方程.【解析】(1)由 得
又所求直线l与直线3x+y-1=0平行,
故所求l的方程为
解得15x+5y+16=0.(2)由 得
又所求直线l与直线3x-2y+4=0垂直,
故所求l的方程为
即:14x+21y-15=0.【例】试求三条直线l1:x+y+a=0, l2:x+ay+1=0, l3:ax+y+1=0构成三角形的条件.
【审题指导】若三条直线构成三角形,则任意两条直线相交且不能交于一点.【规范解答】方法一:当a=0时,显然满足条件.当a≠0时,由任意两条直线相交,得
所以a≠±1.
又三条直线不共点,
由 得交点(-1-a,1),
此交点不在直线ax+y+1=0上,
即a(-1-a)+1+1≠0,所以a2+a-2≠0.
所以a≠-2且a≠1.
综上可知,a≠-2且a≠±1.方法二:若三条直线能构成三角形,则三条直线两两相交且不共点,即任意两条直线都不平行且三条直线不共点.
若l1、l2、l3交于一点,则x+y+a=0与x+ay+1=0的交点
(-a-1,1)在直线l3:ax+y+1=0上,
所以a(-a-1)+1+1=0,
所以a=1或a=-2.若l1∥l2,则有 且a≠0,所以a=1;
若l1∥l3,则有-a=-1,所以a=1;
若l2∥l3,则有 且a≠0,所以a=±1.
所以当l1、l2、l3构成三角形时,a≠±1且a≠-2.【变式备选】三条直线l1:x-y=0,l2:x+y-2=0,
l3:5x-ky-15=0构成一个三角形,求k的取值范围.【解析】(1)当l1∥l3时,知k≠0且有
所以有k=5.
(2)当l2∥l3时知k≠0且有
所以有k=-5.(3)当l1,l2,l3三线交于一点时,
解方程组 得
直线l1与l2相交于点(1,1).
又l3过点(1,1),
所以有5×1-k-15=0,
所以有k=-10.
综上可知,要使三条直线构成一个三角形,
需有k≠±5且k≠-10.【典例】(12分)已知△ABC的顶点A(5,1),AB边上的中线CM所在的直线方程为2x-y-5=0,AC边上的高BH所在的直线方程为x-2y-5=0.求:
(1)顶点C的坐标; (2)直线BC的方程.
【审题指导】直线CM的方程已知,只需再寻找一条过点C的直线联立求解便可求出顶点C的坐标,而利用点斜式可求出AC的方程;高BH所在的直线方程已知,AB边上的中线CM所在的直线方程已知,故利用中点坐标公式求点B的坐标,进而利用两点式求直线BC的方程.【规范解答】(1)∵AC边上的高BH所在的直线方程为
x-2y-5=0,故可设直线AC的方程为
2x+y+c=0.又过点A(5,1),
所以10+1+c=0,解得c=-11. ……………………………3分
即直线AC的方程为2x+y-11=0.
由 得
即顶点C的坐标为(4,3). …………………………… 5分(2)设点B的坐标为(x,y),则线段AB的中点
在直线2x-y-5=0上.
即 ①………………… 8分
又点B满足方程x-2y-5=0 ②
联立①②解得x=-1,y=-3.
即点B的坐标为(-1,-3). …………………………… 10分
由两点式求得直线BC的方程为:
6x-5y-9=0. ……………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】过点P(0,1)作一条直线l,使它与两已知直线l1:x-3y+10=0和l2:2x+y-8=0分别交于A、B两点,若线段AB被P点平分,求直线l的方程.
【解题提示】设出A、B两点的坐标,利用线段AB被P点平分这个条件求解该问题.【解析】由已知可设A(3b-10,b),B(a,-2a+8),
∵P是AB的中点,
即
解得a=4,b=2. 即A(-4,2).
又直线l过P、A两点,由两点式求得直线l的方程为
x+4y-4=0.1.下列各组直线中,互相垂直的一组是( )
(A)2x-3y-5=0与4x-6y-5=0
(B)2x-3y-5=0与4x+6y+5=0
(C)2x+3y-6=0与3x-2y+6=0
(D)2x+3y-6=0与2x-3y-6=0
【解析】选C.利用A1A2+B1B2=0逐一验证便可.2.下列直线中,与直线2x-y+3=0相交的是( )
(A)4x-2y-6=0 (B)y=2x-1
(C)y=2x+5 (D)y=-2x-3
【解析】选D.只要直线的斜率与直线2x-y+3=0的斜率不相等,则两直线便相交.经验证选D.3.直线l:y-1=k(x+2)必过定点__________.
【解析】结合直线方程的点斜式可知,直线l必过定点
(-2,1).
答案:(-2,1)4.直线x+2y-2=0与直线2x+y-3=0的交点坐标为__________.
【解析】由方程组 解得
因此两直线交点坐标为
答案: 5.已知直线l1:Ax+3y+C=0,l2:2x-3y+4=0,若l1、l2的交点在y轴上,则C的值为__________.
【解析】设l1与l2的交点为P(x,y),
由题意可知x=0,
又点P在l2上, 即
把点P代入l1,得
解得C=-4.
答案:-46.已知△ABC三边所在直线方程分别为AB:3x+4y+12=0, BC:4x-3y+16=0,CA:2x+y-2=0,求AC边上的高所在的直线方程.
【解析】由 解得交点B(-4,0),
设BD为AC边上的高,则
∴AC边上的高BD所在的直线的方程为
即x-2y+4=0.一、选择题(每题4分,共16分)
1.直线2x+3y+1=0和直线3x+2y-4=0的位置关系为( )
(A)平行 (B)垂直
(C)相交但不垂直 (D)以上都不对
【解析】选C.直线2x+3y+1=0的斜率为 直线3x+2y-4=0
的斜率为 显然两直线相交但不垂直.2.设集合A={(x,y)|y=ax+1}, B={(x, y)|y=x+b},且A∩B={(2,5)},则( )
(A)a=3,b=2 (B)a=2,b=3
(C)a=-3,b=-2 (D)a=-2,b=-3
【解析】选B.由题意可知(2,5)是直线与直线的交点坐标,故5=2a+1,5=2+b,解得a=2,b=3.选B.3.若直线Ax-2y-1=0与直线6x-4y+C=0平行,则( )
(A)A=3,C=-2 (B)A=3,C≠-2
(C)A≠3,C=-2 (D)A≠3,C≠-2
【解析】选B.两直线平行只需满足
便可,解得A=3,C≠-2.4.当m取不同实数时,方程mx-y+2m+1=0表示的几何图形具有的特征是( )
(A)都经过第一象限
(B)组成一个封闭的图形
(C)表示直角坐标平面内的所有直线
(D)相交于一点
【解析】选D.方程可化为m(x+2)-y+1=0,表示当m取不同实数时,直线恒过点(-2,1).选D. 【方法技巧】直线恒过定点问题的求解策略
求解策略一:该类问题常常涉及到不论参数m取何值,直线系恒过定点,此时我们可以抓住“不论参数m取何值”这一条件,对参数m取特殊值,这样就把变的问题转化成了定的问题.求解策略二:逆用过定点的直线系求解,即把含参数的放
在一起,不含参数的放在一起.构造成 (A1x+B1y+C1)+m(A2x
+B2y+C2)=0(m∈R)的形式,然后解方程组
便可(m∈R).二、填空题(每题4分,共8分)
5.直线mx+10y=2与3x+(n-1)y=-1重合,则m=__________, n=__________.
【解析】由题意可知
解得m=-6,n=-4.
答案: -6 -46.三条直线ax+2y+8=0,4x+3y=10和2x-y=10相交于一点,则a的值为__________.
【解析】由 得
∴点(4,-2)在ax+2y+8=0上,
∴a=-1.
答案:-1三、解答题(每题8分,共16分)
7.求经过直线l1:2x+3y-5=0,l2:3x-2y-3=0的交点且平行于直线2x+y-3=0的直线方程.
【解析】由 得
因为所求直线平行于直线2x+y-3=0,故可设所求直线的方程
为2x+y+c=0,把点 代入得
故所求直线的方程为26x+13y-47=0.8.已知直线l经过直线3x+4y-2=0与直线2x+y+2=0的交点P,且垂直于直线x-2y-1=0.
(1)求直线l的方程;
(2)求直线l与两坐标轴围成的三角形的面积S.【解析】(1)由 解得
∴点P的坐标是(-2,2).
又所求直线l与x-2y-1=0垂直,
可设直线l的方程为2x+y+C=0.
把点P的坐标代入得2×(-2)+2+C=0,即C=2.
∴所求直线l的方程为2x+y+2=0.
(2)由直线l的方程知它在x轴、y轴上的截距分别是-1、-2,
所以直线l与两坐标轴围成三角形的面积【挑战能力】
(10分)已知直线l1:3x+my-1=0,l2:3x-2y-5=0,l3:6x+y-5=0,
(1)若这三条直线交于一点,求m的值;
(2)若三条直线能构成三角形,求m的值.
【解题提示】求解(2)时可从反面考虑三条直线什么时候不能构成三角形,然后考虑其补集.【解析】(1)由 得 代入l1得,m=2;
(2)当三条直线交于一点或其中两条互相平行时,它们不能构成三角形.
①由(1)得,当m=2时三线共点,不能构成三角形;
②当l1∥l2时,m=-2,
当l1∥l3时,
此时它们不能构成三角形.
综上所述:当m≠±2且 时,三条直线能构成三角形.
研究两条直线l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0的位置关系(相交、重合、平行)可以转化为两条直线方程所得的方程
组 的解的个数问题.具体情况如下:两直线位置关系的判断 2.两条直线相交的判定方法:
若只判断两直线是否相交采用方法(1)较方便,若要求交点坐标则采用方法(2).【例1】分别判断下列直线的位置关系,若相交,求出它们的交点:
(1)l1:2x-y=7,l2:3x+2y-7=0;
(2)l1:2x-6y+4=0,l2:4x-12y+8=0;
(3)l1:4x+2y+4=0,l2:y=-2x+3.
【审题指导】思路一:利用方程组的观点判断直线的位置关系,并求交点;思路二:利用斜率的关系判断直线的位置关系,若相交再利用方程组求交点.【规范解答】方法一:(1)∵
的解为
∴直线l1与l2相交,交点坐标为(3,-1).
(2)∵ 有无数组解,
∴ l1和l2重合.
(3)∵ 无解,∴l1∥l2.方法二:(1)∵l1:2x-y=7,l2:3x+2y-7=0的斜率不相等,
故两直线相交.由
解得
∴直线l1与l2的交点坐标为(3,-1).(2)∵l1:2x-6y+4=0,l2:4x-12y+8=0
且 ∴l1和l2重合.
(3)∵ l1 :4x+2y+4=0,
l2:y=-2x+3即2x+y-3=0且
∴l1∥l2.【互动探究】把本题(1)“l1:2x-y=7”换成“l1:ax-y=7”求相应问题.
【解题提示】解方程组,按方程是否有解对参数a进行讨论.【解析】由 得(3+2a)x=21.
当 时,原方程组无解,∴l1∥l2.
当 时,原方程组有且只有一解
∴直线l1与l2相交,交点坐标为 利用两直线的位置关系求参数值的方法:
已知直线的一般式且明确了直线间的关系求参数的值(或范围)时,其求解思路为:利用两直线的位置关系求参数的值 上述一般式给出的方程,其平行和重合的条件务必分清.【例2】已知两条直线l1:x+my+6=0, l2:(m-2)x+3y+2m=0问:当m为何值时,l1与l2
(1)平行; (2)垂直; (3)重合.
【审题指导】方程以一般式的形式给出,直接应用两直线平行、垂直、重合的等价条件求解.【规范解答】(1)∵l1∥l2
∴3-m(m-2)=0.
即m2-2m-3=0.∴m=-1或m=3.
经检验当m=3时两直线重合,故m=3舍去.
∴m=-1.
(2)∵l1⊥l2,∴1×(m-2)+3m=0,
(3)由(1)可知当m=3时两直线重合.【变式训练】已知直线l1:(k-3)x+(4-k)y+1=0,与
l2:2(k-3)x-2y+3=0平行,则k的值为( )
(A)1或3 (B)1或5
(C)3或5 (D)1或2
【解析】选C.方法一:当k=3时,两直线平行,当k≠3时,
由两直线平行,斜率相等,得: 解得:k=5.
方法二:由-2(k-3)-2(k-3)(4-k)=0得k=3或k=5.
经验证当k=3或k=5时均合题意. 线共点问题的求解方法
(1)方程组法:选择两条较易求解交点的直线方程联立,求出相应交点的坐标P(x0,y0),然后把P(x0,y0)代入另一条直线方程,利用方程的思想求解参数.过交点的直线系(2)直线系法:①经过两直线l1:A1x+B1y+C1=0(A12+B12≠0)和l2:A2x+B2y+C2=0(A22+B22≠0)交点的直线系为m(A1x+B1y+C1) +n(A2x+B2y+C2)=0(其中m,n为参数,m2+n2≠ 0).
当m=1,n=0时,方程即为l1的方程;
当m=0,n=1时,方程即为l2的方程;②上面的直线系可改写成(A1x+B1y+C1)+λ(A2x+B2y+C2)=0 (其中λ∈R).但是此方程中不包括直线l2,这个参数方程形式在解题中较为常用.
比较两种方法可知,如果多条直线交于一点,采用过交点的直线系求解相交问题较简单.③直线系方程(A1x+B1y+C1)+λ(A2x+B2y+C2)=0中,由①、②
可知,此直线系方程恒过定点
④方程y-y0=k(x-x0),由点斜式知,它恒过定点(x0,y0),也
可以化为(y-y0)-k(x-x0)=0,
过定点 即(x0,y0). (1)与直线Ax+By+C=0垂直的直线的方程可设为Bx-Ay+m=0,其中m待定.
(2)与直线Ax+By+C=0平行的直线的方程可设为Ax+By+m=0,其中m待定.【例3】已知直线l1:3x-y-1=0,l2:x+y-3=0,求:
(1)直线l1与l2的交点P的坐标;
(2)过点P且与l1垂直的直线方程.
【审题指导】由于本题l1,l2的方程已知,可利用解方程组的方法求出交点P,进而再求出所求的直线方程.【规范解答】(1)解方程组 得
所以直线l1与l2的交点P的坐标为(1,2).
(2)方法一:直线l1的斜率为3,故过点P且与l1垂直的直线方程
为 即为x+3y-7=0.
方法二:由题意可设所求直线的方程为
3x-y-1+λ(x+y-3)=0,整理得
(3+λ)x+(λ-1)y-1-3λ=0,
又∵该直线与l1垂直,故3×(3+λ)+(-1)×(λ-1)=0,
解得λ=-5.即所求直线的方程为x+3y-7=0.【变式训练】(1)已知直线l经过两条直线2x-3y-3=0和x+y+2=0的交点,且与直线3x+y-1=0平行,求直线l的方程.
(2)已知直线l经过两条直线2x-2y+10=0和3x+4y-2=0的交点,且垂直于直线3x-2y+4=0,求直线l的方程.【解析】(1)由 得
又所求直线l与直线3x+y-1=0平行,
故所求l的方程为
解得15x+5y+16=0.(2)由 得
又所求直线l与直线3x-2y+4=0垂直,
故所求l的方程为
即:14x+21y-15=0.【例】试求三条直线l1:x+y+a=0, l2:x+ay+1=0, l3:ax+y+1=0构成三角形的条件.
【审题指导】若三条直线构成三角形,则任意两条直线相交且不能交于一点.【规范解答】方法一:当a=0时,显然满足条件.当a≠0时,由任意两条直线相交,得
所以a≠±1.
又三条直线不共点,
由 得交点(-1-a,1),
此交点不在直线ax+y+1=0上,
即a(-1-a)+1+1≠0,所以a2+a-2≠0.
所以a≠-2且a≠1.
综上可知,a≠-2且a≠±1.方法二:若三条直线能构成三角形,则三条直线两两相交且不共点,即任意两条直线都不平行且三条直线不共点.
若l1、l2、l3交于一点,则x+y+a=0与x+ay+1=0的交点
(-a-1,1)在直线l3:ax+y+1=0上,
所以a(-a-1)+1+1=0,
所以a=1或a=-2.若l1∥l2,则有 且a≠0,所以a=1;
若l1∥l3,则有-a=-1,所以a=1;
若l2∥l3,则有 且a≠0,所以a=±1.
所以当l1、l2、l3构成三角形时,a≠±1且a≠-2.【变式备选】三条直线l1:x-y=0,l2:x+y-2=0,
l3:5x-ky-15=0构成一个三角形,求k的取值范围.【解析】(1)当l1∥l3时,知k≠0且有
所以有k=5.
(2)当l2∥l3时知k≠0且有
所以有k=-5.(3)当l1,l2,l3三线交于一点时,
解方程组 得
直线l1与l2相交于点(1,1).
又l3过点(1,1),
所以有5×1-k-15=0,
所以有k=-10.
综上可知,要使三条直线构成一个三角形,
需有k≠±5且k≠-10.【典例】(12分)已知△ABC的顶点A(5,1),AB边上的中线CM所在的直线方程为2x-y-5=0,AC边上的高BH所在的直线方程为x-2y-5=0.求:
(1)顶点C的坐标; (2)直线BC的方程.
【审题指导】直线CM的方程已知,只需再寻找一条过点C的直线联立求解便可求出顶点C的坐标,而利用点斜式可求出AC的方程;高BH所在的直线方程已知,AB边上的中线CM所在的直线方程已知,故利用中点坐标公式求点B的坐标,进而利用两点式求直线BC的方程.【规范解答】(1)∵AC边上的高BH所在的直线方程为
x-2y-5=0,故可设直线AC的方程为
2x+y+c=0.又过点A(5,1),
所以10+1+c=0,解得c=-11. ……………………………3分
即直线AC的方程为2x+y-11=0.
由 得
即顶点C的坐标为(4,3). …………………………… 5分(2)设点B的坐标为(x,y),则线段AB的中点
在直线2x-y-5=0上.
即 ①………………… 8分
又点B满足方程x-2y-5=0 ②
联立①②解得x=-1,y=-3.
即点B的坐标为(-1,-3). …………………………… 10分
由两点式求得直线BC的方程为:
6x-5y-9=0. ……………………………………………12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】过点P(0,1)作一条直线l,使它与两已知直线l1:x-3y+10=0和l2:2x+y-8=0分别交于A、B两点,若线段AB被P点平分,求直线l的方程.
【解题提示】设出A、B两点的坐标,利用线段AB被P点平分这个条件求解该问题.【解析】由已知可设A(3b-10,b),B(a,-2a+8),
∵P是AB的中点,
即
解得a=4,b=2. 即A(-4,2).
又直线l过P、A两点,由两点式求得直线l的方程为
x+4y-4=0.1.下列各组直线中,互相垂直的一组是( )
(A)2x-3y-5=0与4x-6y-5=0
(B)2x-3y-5=0与4x+6y+5=0
(C)2x+3y-6=0与3x-2y+6=0
(D)2x+3y-6=0与2x-3y-6=0
【解析】选C.利用A1A2+B1B2=0逐一验证便可.2.下列直线中,与直线2x-y+3=0相交的是( )
(A)4x-2y-6=0 (B)y=2x-1
(C)y=2x+5 (D)y=-2x-3
【解析】选D.只要直线的斜率与直线2x-y+3=0的斜率不相等,则两直线便相交.经验证选D.3.直线l:y-1=k(x+2)必过定点__________.
【解析】结合直线方程的点斜式可知,直线l必过定点
(-2,1).
答案:(-2,1)4.直线x+2y-2=0与直线2x+y-3=0的交点坐标为__________.
【解析】由方程组 解得
因此两直线交点坐标为
答案: 5.已知直线l1:Ax+3y+C=0,l2:2x-3y+4=0,若l1、l2的交点在y轴上,则C的值为__________.
【解析】设l1与l2的交点为P(x,y),
由题意可知x=0,
又点P在l2上, 即
把点P代入l1,得
解得C=-4.
答案:-46.已知△ABC三边所在直线方程分别为AB:3x+4y+12=0, BC:4x-3y+16=0,CA:2x+y-2=0,求AC边上的高所在的直线方程.
【解析】由 解得交点B(-4,0),
设BD为AC边上的高,则
∴AC边上的高BD所在的直线的方程为
即x-2y+4=0.一、选择题(每题4分,共16分)
1.直线2x+3y+1=0和直线3x+2y-4=0的位置关系为( )
(A)平行 (B)垂直
(C)相交但不垂直 (D)以上都不对
【解析】选C.直线2x+3y+1=0的斜率为 直线3x+2y-4=0
的斜率为 显然两直线相交但不垂直.2.设集合A={(x,y)|y=ax+1}, B={(x, y)|y=x+b},且A∩B={(2,5)},则( )
(A)a=3,b=2 (B)a=2,b=3
(C)a=-3,b=-2 (D)a=-2,b=-3
【解析】选B.由题意可知(2,5)是直线与直线的交点坐标,故5=2a+1,5=2+b,解得a=2,b=3.选B.3.若直线Ax-2y-1=0与直线6x-4y+C=0平行,则( )
(A)A=3,C=-2 (B)A=3,C≠-2
(C)A≠3,C=-2 (D)A≠3,C≠-2
【解析】选B.两直线平行只需满足
便可,解得A=3,C≠-2.4.当m取不同实数时,方程mx-y+2m+1=0表示的几何图形具有的特征是( )
(A)都经过第一象限
(B)组成一个封闭的图形
(C)表示直角坐标平面内的所有直线
(D)相交于一点
【解析】选D.方程可化为m(x+2)-y+1=0,表示当m取不同实数时,直线恒过点(-2,1).选D. 【方法技巧】直线恒过定点问题的求解策略
求解策略一:该类问题常常涉及到不论参数m取何值,直线系恒过定点,此时我们可以抓住“不论参数m取何值”这一条件,对参数m取特殊值,这样就把变的问题转化成了定的问题.求解策略二:逆用过定点的直线系求解,即把含参数的放
在一起,不含参数的放在一起.构造成 (A1x+B1y+C1)+m(A2x
+B2y+C2)=0(m∈R)的形式,然后解方程组
便可(m∈R).二、填空题(每题4分,共8分)
5.直线mx+10y=2与3x+(n-1)y=-1重合,则m=__________, n=__________.
【解析】由题意可知
解得m=-6,n=-4.
答案: -6 -46.三条直线ax+2y+8=0,4x+3y=10和2x-y=10相交于一点,则a的值为__________.
【解析】由 得
∴点(4,-2)在ax+2y+8=0上,
∴a=-1.
答案:-1三、解答题(每题8分,共16分)
7.求经过直线l1:2x+3y-5=0,l2:3x-2y-3=0的交点且平行于直线2x+y-3=0的直线方程.
【解析】由 得
因为所求直线平行于直线2x+y-3=0,故可设所求直线的方程
为2x+y+c=0,把点 代入得
故所求直线的方程为26x+13y-47=0.8.已知直线l经过直线3x+4y-2=0与直线2x+y+2=0的交点P,且垂直于直线x-2y-1=0.
(1)求直线l的方程;
(2)求直线l与两坐标轴围成的三角形的面积S.【解析】(1)由 解得
∴点P的坐标是(-2,2).
又所求直线l与x-2y-1=0垂直,
可设直线l的方程为2x+y+C=0.
把点P的坐标代入得2×(-2)+2+C=0,即C=2.
∴所求直线l的方程为2x+y+2=0.
(2)由直线l的方程知它在x轴、y轴上的截距分别是-1、-2,
所以直线l与两坐标轴围成三角形的面积【挑战能力】
(10分)已知直线l1:3x+my-1=0,l2:3x-2y-5=0,l3:6x+y-5=0,
(1)若这三条直线交于一点,求m的值;
(2)若三条直线能构成三角形,求m的值.
【解题提示】求解(2)时可从反面考虑三条直线什么时候不能构成三角形,然后考虑其补集.【解析】(1)由 得 代入l1得,m=2;
(2)当三条直线交于一点或其中两条互相平行时,它们不能构成三角形.
①由(1)得,当m=2时三线共点,不能构成三角形;
②当l1∥l2时,m=-2,
当l1∥l3时,
此时它们不能构成三角形.
综上所述:当m≠±2且 时,三条直线能构成三角形.
