2.3.1-2.3.2 空间直角坐标系的建立和空间直角坐标系中点的坐标 课件1
文档属性
| 名称 | 2.3.1-2.3.2 空间直角坐标系的建立和空间直角坐标系中点的坐标 课件1 |  | |
| 格式 | zip | ||
| 文件大小 | 763.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-22 15:10:02 | ||
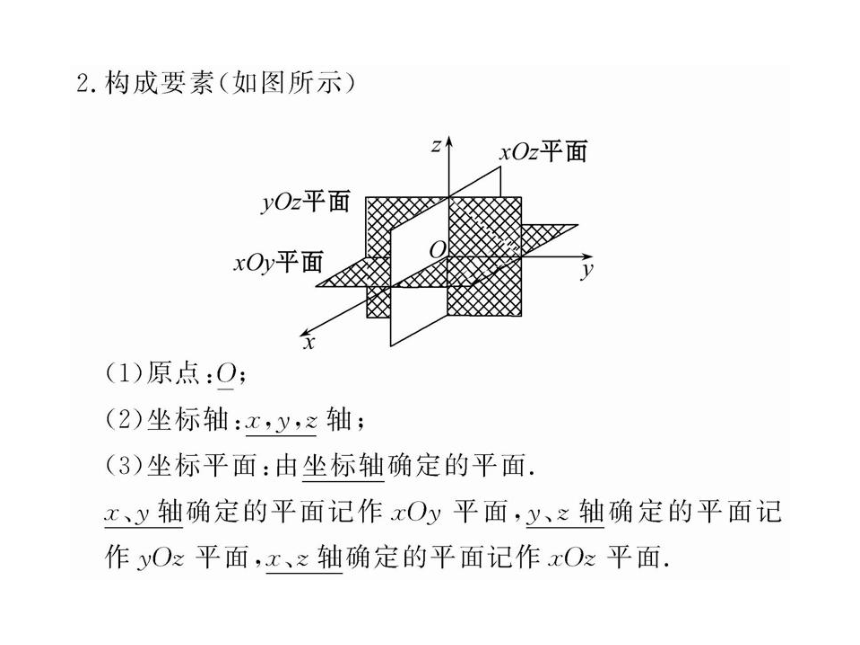
图片预览










文档简介
课件56张PPT。2.3.1 空间直角坐标系的建立
2.3.2 空间直角坐标系中点的坐标1.已知点M的位置,求其坐标的方法:
过M作MM1垂直于平面xOy,垂足为M1,求出M1的x坐标和y坐标,再由射线M1M的指向和线段M1M的长度确定z坐标.点的坐标的确定 2.特殊位置的点的坐标形成
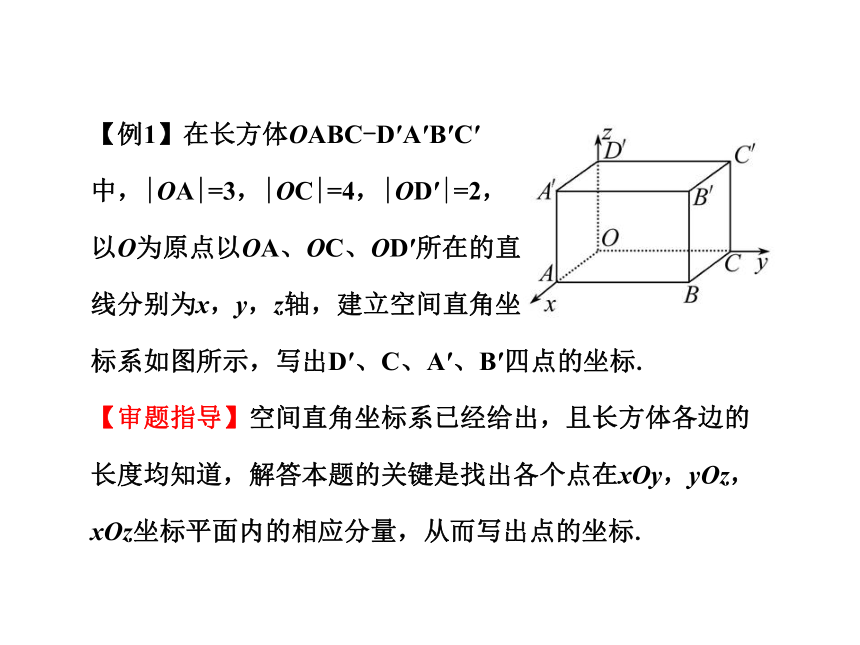
在空间直角坐标系中,三条坐标轴和三个坐标平面上的点的坐标形式如下表所示.其中x,y,z∈R.【例1】在长方体OABC-D′A′B′C′
中,|OA|=3,|OC|=4,|OD′|=2,
以O为原点以OA、OC、OD′所在的直
线分别为x,y,z轴,建立空间直角坐
标系如图所示,写出D′、C、A′、B′四点的坐标.
【审题指导】空间直角坐标系已经给出,且长方体各边的长度均知道,解答本题的关键是找出各个点在xOy,yOz,xOz坐标平面内的相应分量,从而写出点的坐标.【规范解答】因为D′在z轴上,且|OD′|=2,则它的z坐标为2,它的x,y坐标都是0,所以D′点的坐标是(0,0,2),点C在y轴上,且|OC|=4,所以点C的坐标为(0,4,0),点A′的坐标为(3,0,2),点B′的坐标为(3,4,2).【互动探究】在题设条件不变的情况下,求棱BB′中点的坐标.
【解题提示】求出点B的坐标,然后求棱BB′中点的坐标.
【解析】∵点B在xOy平面内,且|OA|=3,|OC|=4,∴B(3,4,0).
又∵B′的坐标为(3,4,2),
∴棱BB′中点的坐标为(3,4,1).【例】已知正四棱锥P-ABCD的底面边长为4,侧棱长为10,试建立适当的空间直角坐标系,写出各顶点的坐标.
【审题指导】四棱锥P-ABCD是正四棱锥,解答时可先由条件求出正四棱锥的高,再根据正四棱锥的对称性,建立适当的空间直角坐标系.【规范解答】∵正四棱锥P-ABCD的底面边长为4,侧棱长为10,
∴正四棱锥的高为
以正四棱锥的底面中心为原点,
平行于AB、BC所在的直线分别为
y轴、x轴,建立如图所示的空间
直角坐标系,则正四棱锥各顶点的坐标分别为
A(2,-2,0)、B(2,2,0)、C(-2,2,0)、
D(-2,-2,0)、【变式备选】如图,在四棱锥P-ABCD中,底面ABCD为正方形,且边长为2a,棱PD⊥底面ABCD,PD=2b,取各侧棱的中点E,F,G,H,写出点E,F,G,H的坐标.【解析】由图形知,DA⊥DC,DC⊥DP,DP⊥DA,故以D为原点,建立如图所示的空间直角坐标
系.
因为E,F,G,H分别为侧棱中点,
由立体几何知识可知,平面EFGH与
底面ABCD平行,从而这4个点的z坐标都为P的z坐标的一半,也就是b,由H为DP中点,得H(0,0,b);E在底面上的投影为AD中点,所以E的x坐标和y坐标分别为a和0,所以E(a,0,b),同理G(0,a,b);F在坐标平面xDz和yDz上的投影分别为点E和G,故F与E的x坐标相同都是a,与G的y坐标也相同为a,又F的z坐标为b,故F(a,a,b).已知点M的坐标(x0,y0,z0),确定它的位置的方法有:
1.先在x轴上取横坐标为x0的点M1;再将M1在xOy平面内沿与y轴平行的方向的负向(y0<0)或正向(y0>0)平移|y0|个单位,得到点M2;再将点M2沿与z轴平行的方向的正向
(z0>0)或负向(z0<0)平移|z0|个单位,就可得到点M(x0,y0,z0).已知点的坐标确定点的位置2.以原点O为一个顶点,构造棱长分别为|x0|,|y0|,|z0|的长方体(三条棱的位置要与x0,y0,z0的符号一致),则长方体与O相对的顶点即为所求的点M.
3.先在x轴上找到点M1(x0,0,0),过M1作x轴的垂直平面α;再在y轴上找到点M2(0,y0,0),过M2作y轴的垂直平面β;在z轴上找到点M3(0,0,z0),过M3作z轴的垂直平面γ,三个平面α、β、γ交于一点,此交点即为所求点M. 在某一坐标平面内确定点的位置时,可以参考平面直角坐标系中的有关方法.【例2】在空间直角坐标系中,作出点M(4,-2,5).
【审题指导】解答本题可有三种思路:
①利用平移点的方法,将原点按坐标轴的方向三次平移得点M;
②构造适合条件的长方体,使三条棱长分别为4,2,5,通过和原点相对的顶点确定M的位置;
③通过作三个分别与坐标轴垂直的平面,由平面的交点确定点M.【规范解答】方法一:将原点
沿x轴正方向平移4个单位得点
M1(4,0,0),再把M1沿与y轴
平行的直线且与y轴相反方向
平移2个单位,得到点M2(4,-2,0),最后把M2沿与z轴平行的直线且与z轴相同方向平移5个单位即得点M.方法二:以O为顶点构造长方体,使
这个长方体在点O处的三条棱分别在
x轴正半轴、y轴负半轴、z轴正半轴
上,且棱长分别为4,2,5.则长方
体中顶点O相对的顶点即为所求的点M.方法三:在x轴上找到x坐标为4的点,过此点作与x轴垂直的平面α;在y轴上找到y坐标为-2的点,过此点作与y轴垂直的平面β;在z轴上找到z坐标为5的点,过此点作与z轴垂直的平面γ,则α、β、γ交于一点,此交点即为所求的点M.【变式训练】点P(3,2,0)在空间直角坐标系中的位置是在( )
(A)z轴上 (B)xOy面上
(C)yOz面上 (D)xOz面上
【解析】选B.∵点P(3,2,0)的z坐标为0,
∴点P(3,2,0)在xOy面上,选B. 空间直角坐标系中,有关点的坐标对称问题
P(x,y,z)关于坐标平面xOy对称的点P1(x,y,-z);
P(x,y,z)关于坐标平面yOz对称的点P2(-x,y,z);
P(x,y,z)关于坐标平面xOz对称的点P3(x,-y,z);
P(x,y,z)关于x轴对称的点P4(x,-y,-z);
P(x,y,z)关于y轴对称的点P5(-x,y,-z);
P(x,y,z)关于z轴对称的点P6(-x,-y,z).点的对称问题【例3】如图所示,正方体ABCD-A1B1C1D1
的棱长为a.
(1)求B1关于平面xOy对称的点的坐标;
(2)求B1关于z轴对称的点的坐标;
(3)求B1关于原点对称的点的坐标.
【审题指导】坐标系已经给出,解答本题只需先求出点B1的坐标,在此基础上借助点关于点、线、平面的对称原则求解便可.【规范解答】∵正方体ABCD-A1B1C1D1的棱长为a,
∴易求得点B1的坐标为(a,a,a).
(1)B1关于平面xOy对称的点的坐标为(a,a,-a);
(2)B1关于z轴对称的点的坐标为(-a,-a,a);
(3)B1关于原点对称的点的坐标为(-a,-a,-a).【变式训练】求点A(1,2,-1)关于坐标平面xOy及x轴对称的点的坐标.
【解题提示】发挥空间想象能力,结合图形可写A点对称点的坐标,但要注意各坐标的符号.【解析】如图所示,过A作AM⊥xOy交平面于M,并延长到C,使AM=CM,则A与C关于坐标平面xOy对称,且C(1,2,1).
过A作AN⊥x轴于N并延长到点B,
使AN=NB,
则A与B关于x轴对称,且B(1,-2,1).
∴A(1,2,-1)关于坐标平面xOy对称的点是C(1,2,1),
A(1,2,-1)关于x轴对称的点是B(1,-2,1).【典例】(12分)四面体P-ABC是一个
正方体截下的一角,且满足|PA|=a,
|PB|=b,|PC|=c,建立如图所示的空
间直角坐标系,求△ABC的重心G的坐
标.
【审题指导】几何体的形状已知,且坐标系已给出.求解本题的关键是依据题设条件正确写出△ABC的顶点坐标,进而借助重心坐标公式求出点G的坐标.【规范解答】 由图可知P点为坐标原点,点A,B,C分别在x,y,z轴上,且|PA|=a,|PB|=b,|PC|=c,
∴A(a,0,0),B(0,b,0),C(0,0,c). ……………………5分
设△ABC的重心G的坐标为(x,y,z),
则 …………………………………10分
即重心G的坐标为 ………………………… 12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】如图,三棱柱ABC-A1B1C1中,
所有棱长都为2,侧棱AA1⊥底面ABC,建
立适当坐标系写出各顶点的坐标.
【解题提示】题中给出了三棱柱的
棱长,要求各顶点的坐标,可以以AC的中点为原点找出两两垂直的三条线分别为x、y、z轴建系,然后确定各点坐标.【解析】取AC的中点O和A1C1的中点O1,
可得BO⊥AC,分别以OB、OC、OO1为x、
y、z轴建立空间直角坐标系.
因为三棱柱各棱长均为2,所以OA=OC=1,
可得1.点Q(0,0,3)的位置是( )
(A)在x轴上 (B)在y轴上
(C)在z轴上 (D)在面xOy上
【解析】选C.z轴上的坐标满足x=y=0.2.点(2,-1,3)与点(2,-1,-3)( )
(A)关于x轴对称 (B)关于y轴对称
(C)关于xOy平面对称 (D)关于z轴对称
【解析】选C.点(2,-1,3)与点(2,-1,-3)的x坐标,y坐标相同,z坐标互为相反数,故这两点关于xOy平面对称.3.点P(1,2,-1)在xOz平面内的垂足为B(x,y,z),则x+y+z=( )
(A)3 (B)2
(C)1 (D)0
【解析】选D.点P(1,2,-1)在xOz平面的垂足为B(1,0, -1),∴x+y+z=1+0-1=0.4.已知正方体ABCD-A1B1C1D1,点A的坐标为(0,0,0),C1的坐标为(1,1,1),则线段AC1的中点坐标为__________.
【解析】结合中点坐标公式易得线段AC1的中点坐标为
答案: 5.在空间直角坐标系中,作出点M(6,-2,4).
【解析】点M的位置可按如下步骤作出:
先在x轴上作出横坐标是6的点M1,再将
M1沿与y轴平行的方向向左移动2个单位
得到点M2,然后将M2沿与z轴平行的方
向向上移动4个单位即得点M,M点的位置如图所示.一、选择题(每题4分,共16分)
1.在空间直角坐标系O-xyz中,点P(-2,0,3)位于( )
(A)xOz平面内 (B)yOz平面内
(C)y轴上 (D)z轴上
【解析】选A.∵点P(-2,0,3)的y坐标为零,
∴点P(-2,0,3)在xOz平面内.2.已知点A(-3,1,4),则点A关于原点的对称点的坐标为
( )
(A)(1,-3,-4) (B)(-4,1,-3)
(C)(3,-1,-4) (D)(4,-1,3)
【解析】选C.点A关于原点的对称点的坐标为(3,-1,-4).3.在空间直角坐标系中,已知点P(1,2,3),过P作平面xOy的垂线PQ,则垂足Q的坐标为( )
(A)(0,2,0) (B)(1,2,0)
(C)(1,0,3) (D)(0,2,3)
【解题提示】垂足Q的坐标,即为点P(1,2,3)在平面xOy内的射影.
【解析】选B.因为过P作平面xOy的垂线PQ,则垂足Q在xOy平面内,故满足z=0,x,y不变.故选B.4.以正方体ABCD-A1B1C1D1的棱AB、AD、AA1所在的直线为坐标轴建立空间直角坐标系,且正方体的棱长为一个单位长度,则棱CC1中点坐标为( )
(A)( ,1,1) (B)(1, ,1)
(C)(1,1, ) (D)( , ,1)
【解析】选C.由题可知点C(1,1,0),C1(1,1,1),
∴棱CC1中点坐标为(1,1, ).二、填空题(每题4分,共8分)
5.写出点P(2,3,4)在三条坐标轴上的射影的坐标_________,________,_________.
【解析】点P(2,3,4)在x,y,z轴上的射影的坐标分别为(2,0,0),(0,3,0),(0,0,4).
答案:(2,0,0) (0,3,0) (0,0,4)6.如图所示的
空间直角坐标系中,正方体棱长为2,
|PQ|=3|PR|,则点R的空间直角坐标
为__________.
【解题提示】充分借助平面几何的性质及条件|PQ|=
3|PR|求点R的坐标.【解析】过点R作RT⊥QT,如图所示,
由|PQ|=3|PR|及相似三角形的知识
可知
同理可求
∴点R的空间直角坐标为
答案: 【方法技巧】巧用平面几何的性质求空间点的坐标
立体几何是平面几何的拓展延伸,求解立体几何中的问题常常利用“降维”的思想,把立体几何问题平面化.如本题中巧用平行线的性质建立点T与点R坐标间的联系从而顺利写出所要求解的点的坐标.三、解答题(每题8分,共16分)
7.已知ABCD为平行四边形,且A(4,1,3),B(2,-5,1),C(3,7,-5),求点D的坐标.
【解题提示】利用平行四边形的对称性求点D的坐标.【解析】∵ABCD为平行四边形,且A(4,1,3),
C(3,7,-5),
∴线段AC的中点坐标为
设点D的坐标为(x,y,z),则对角线BD的中点坐标也为
解得
∴点D的坐标为(5,13,-3).8.如图,已知长方体ABCD-A′B′C′D′的边长为AB=12,AD=8,AA′=5.以这个长方体
的顶点A为坐标原点,射线AB,AD,AA′
分别为x轴、y轴、z轴的正半轴,建
立空间直角坐标系,求长方体各个
顶点的坐标.【解析】因为AB=12,AD=8,AA′=5,点A在坐标原点,即A(0,0,0),且B,D,A′分别在x轴、y轴、z轴上,所以它们的坐标分别为B(12,0,0),D(0,8,0),A′(0,0,5).
点C,B′,D′分别在xOy平面、xOz平面和yOz平面内,坐标分别为C(12,8,0),B′(12,0,5),D′(0,8,5).
点C′在三条坐标轴上的射影分别是点B,D,A′,故点C′的坐标为(12,8,5).【挑战能力】
(10分)(1)在空间直角坐标系O-xyz中,画出不共线的3个点A,B,C,使得这3个点的坐标都满足z=3,并画出图形;
(2)写出由这三个点确定的平面内的点的坐标应满足的条件.【解析】(1)取三个点A(0,0,3),C(4,0,3),B(0,4,3),其图形如图所示:
(2)A,B,C三点不共线,可以确定一
个平面,又因为这三点在xOy平面的同
侧,且到xOy平面的距离相等,所以平
面ABC平行于xOy平面,而且平面ABC内的每一个点在z轴上的射影到原点的距离都等于3,即该平面上的点的坐标都满足z=3.
2.3.2 空间直角坐标系中点的坐标1.已知点M的位置,求其坐标的方法:
过M作MM1垂直于平面xOy,垂足为M1,求出M1的x坐标和y坐标,再由射线M1M的指向和线段M1M的长度确定z坐标.点的坐标的确定 2.特殊位置的点的坐标形成
在空间直角坐标系中,三条坐标轴和三个坐标平面上的点的坐标形式如下表所示.其中x,y,z∈R.【例1】在长方体OABC-D′A′B′C′
中,|OA|=3,|OC|=4,|OD′|=2,
以O为原点以OA、OC、OD′所在的直
线分别为x,y,z轴,建立空间直角坐
标系如图所示,写出D′、C、A′、B′四点的坐标.
【审题指导】空间直角坐标系已经给出,且长方体各边的长度均知道,解答本题的关键是找出各个点在xOy,yOz,xOz坐标平面内的相应分量,从而写出点的坐标.【规范解答】因为D′在z轴上,且|OD′|=2,则它的z坐标为2,它的x,y坐标都是0,所以D′点的坐标是(0,0,2),点C在y轴上,且|OC|=4,所以点C的坐标为(0,4,0),点A′的坐标为(3,0,2),点B′的坐标为(3,4,2).【互动探究】在题设条件不变的情况下,求棱BB′中点的坐标.
【解题提示】求出点B的坐标,然后求棱BB′中点的坐标.
【解析】∵点B在xOy平面内,且|OA|=3,|OC|=4,∴B(3,4,0).
又∵B′的坐标为(3,4,2),
∴棱BB′中点的坐标为(3,4,1).【例】已知正四棱锥P-ABCD的底面边长为4,侧棱长为10,试建立适当的空间直角坐标系,写出各顶点的坐标.
【审题指导】四棱锥P-ABCD是正四棱锥,解答时可先由条件求出正四棱锥的高,再根据正四棱锥的对称性,建立适当的空间直角坐标系.【规范解答】∵正四棱锥P-ABCD的底面边长为4,侧棱长为10,
∴正四棱锥的高为
以正四棱锥的底面中心为原点,
平行于AB、BC所在的直线分别为
y轴、x轴,建立如图所示的空间
直角坐标系,则正四棱锥各顶点的坐标分别为
A(2,-2,0)、B(2,2,0)、C(-2,2,0)、
D(-2,-2,0)、【变式备选】如图,在四棱锥P-ABCD中,底面ABCD为正方形,且边长为2a,棱PD⊥底面ABCD,PD=2b,取各侧棱的中点E,F,G,H,写出点E,F,G,H的坐标.【解析】由图形知,DA⊥DC,DC⊥DP,DP⊥DA,故以D为原点,建立如图所示的空间直角坐标
系.
因为E,F,G,H分别为侧棱中点,
由立体几何知识可知,平面EFGH与
底面ABCD平行,从而这4个点的z坐标都为P的z坐标的一半,也就是b,由H为DP中点,得H(0,0,b);E在底面上的投影为AD中点,所以E的x坐标和y坐标分别为a和0,所以E(a,0,b),同理G(0,a,b);F在坐标平面xDz和yDz上的投影分别为点E和G,故F与E的x坐标相同都是a,与G的y坐标也相同为a,又F的z坐标为b,故F(a,a,b).已知点M的坐标(x0,y0,z0),确定它的位置的方法有:
1.先在x轴上取横坐标为x0的点M1;再将M1在xOy平面内沿与y轴平行的方向的负向(y0<0)或正向(y0>0)平移|y0|个单位,得到点M2;再将点M2沿与z轴平行的方向的正向
(z0>0)或负向(z0<0)平移|z0|个单位,就可得到点M(x0,y0,z0).已知点的坐标确定点的位置2.以原点O为一个顶点,构造棱长分别为|x0|,|y0|,|z0|的长方体(三条棱的位置要与x0,y0,z0的符号一致),则长方体与O相对的顶点即为所求的点M.
3.先在x轴上找到点M1(x0,0,0),过M1作x轴的垂直平面α;再在y轴上找到点M2(0,y0,0),过M2作y轴的垂直平面β;在z轴上找到点M3(0,0,z0),过M3作z轴的垂直平面γ,三个平面α、β、γ交于一点,此交点即为所求点M. 在某一坐标平面内确定点的位置时,可以参考平面直角坐标系中的有关方法.【例2】在空间直角坐标系中,作出点M(4,-2,5).
【审题指导】解答本题可有三种思路:
①利用平移点的方法,将原点按坐标轴的方向三次平移得点M;
②构造适合条件的长方体,使三条棱长分别为4,2,5,通过和原点相对的顶点确定M的位置;
③通过作三个分别与坐标轴垂直的平面,由平面的交点确定点M.【规范解答】方法一:将原点
沿x轴正方向平移4个单位得点
M1(4,0,0),再把M1沿与y轴
平行的直线且与y轴相反方向
平移2个单位,得到点M2(4,-2,0),最后把M2沿与z轴平行的直线且与z轴相同方向平移5个单位即得点M.方法二:以O为顶点构造长方体,使
这个长方体在点O处的三条棱分别在
x轴正半轴、y轴负半轴、z轴正半轴
上,且棱长分别为4,2,5.则长方
体中顶点O相对的顶点即为所求的点M.方法三:在x轴上找到x坐标为4的点,过此点作与x轴垂直的平面α;在y轴上找到y坐标为-2的点,过此点作与y轴垂直的平面β;在z轴上找到z坐标为5的点,过此点作与z轴垂直的平面γ,则α、β、γ交于一点,此交点即为所求的点M.【变式训练】点P(3,2,0)在空间直角坐标系中的位置是在( )
(A)z轴上 (B)xOy面上
(C)yOz面上 (D)xOz面上
【解析】选B.∵点P(3,2,0)的z坐标为0,
∴点P(3,2,0)在xOy面上,选B. 空间直角坐标系中,有关点的坐标对称问题
P(x,y,z)关于坐标平面xOy对称的点P1(x,y,-z);
P(x,y,z)关于坐标平面yOz对称的点P2(-x,y,z);
P(x,y,z)关于坐标平面xOz对称的点P3(x,-y,z);
P(x,y,z)关于x轴对称的点P4(x,-y,-z);
P(x,y,z)关于y轴对称的点P5(-x,y,-z);
P(x,y,z)关于z轴对称的点P6(-x,-y,z).点的对称问题【例3】如图所示,正方体ABCD-A1B1C1D1
的棱长为a.
(1)求B1关于平面xOy对称的点的坐标;
(2)求B1关于z轴对称的点的坐标;
(3)求B1关于原点对称的点的坐标.
【审题指导】坐标系已经给出,解答本题只需先求出点B1的坐标,在此基础上借助点关于点、线、平面的对称原则求解便可.【规范解答】∵正方体ABCD-A1B1C1D1的棱长为a,
∴易求得点B1的坐标为(a,a,a).
(1)B1关于平面xOy对称的点的坐标为(a,a,-a);
(2)B1关于z轴对称的点的坐标为(-a,-a,a);
(3)B1关于原点对称的点的坐标为(-a,-a,-a).【变式训练】求点A(1,2,-1)关于坐标平面xOy及x轴对称的点的坐标.
【解题提示】发挥空间想象能力,结合图形可写A点对称点的坐标,但要注意各坐标的符号.【解析】如图所示,过A作AM⊥xOy交平面于M,并延长到C,使AM=CM,则A与C关于坐标平面xOy对称,且C(1,2,1).
过A作AN⊥x轴于N并延长到点B,
使AN=NB,
则A与B关于x轴对称,且B(1,-2,1).
∴A(1,2,-1)关于坐标平面xOy对称的点是C(1,2,1),
A(1,2,-1)关于x轴对称的点是B(1,-2,1).【典例】(12分)四面体P-ABC是一个
正方体截下的一角,且满足|PA|=a,
|PB|=b,|PC|=c,建立如图所示的空
间直角坐标系,求△ABC的重心G的坐
标.
【审题指导】几何体的形状已知,且坐标系已给出.求解本题的关键是依据题设条件正确写出△ABC的顶点坐标,进而借助重心坐标公式求出点G的坐标.【规范解答】 由图可知P点为坐标原点,点A,B,C分别在x,y,z轴上,且|PA|=a,|PB|=b,|PC|=c,
∴A(a,0,0),B(0,b,0),C(0,0,c). ……………………5分
设△ABC的重心G的坐标为(x,y,z),
则 …………………………………10分
即重心G的坐标为 ………………………… 12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】如图,三棱柱ABC-A1B1C1中,
所有棱长都为2,侧棱AA1⊥底面ABC,建
立适当坐标系写出各顶点的坐标.
【解题提示】题中给出了三棱柱的
棱长,要求各顶点的坐标,可以以AC的中点为原点找出两两垂直的三条线分别为x、y、z轴建系,然后确定各点坐标.【解析】取AC的中点O和A1C1的中点O1,
可得BO⊥AC,分别以OB、OC、OO1为x、
y、z轴建立空间直角坐标系.
因为三棱柱各棱长均为2,所以OA=OC=1,
可得1.点Q(0,0,3)的位置是( )
(A)在x轴上 (B)在y轴上
(C)在z轴上 (D)在面xOy上
【解析】选C.z轴上的坐标满足x=y=0.2.点(2,-1,3)与点(2,-1,-3)( )
(A)关于x轴对称 (B)关于y轴对称
(C)关于xOy平面对称 (D)关于z轴对称
【解析】选C.点(2,-1,3)与点(2,-1,-3)的x坐标,y坐标相同,z坐标互为相反数,故这两点关于xOy平面对称.3.点P(1,2,-1)在xOz平面内的垂足为B(x,y,z),则x+y+z=( )
(A)3 (B)2
(C)1 (D)0
【解析】选D.点P(1,2,-1)在xOz平面的垂足为B(1,0, -1),∴x+y+z=1+0-1=0.4.已知正方体ABCD-A1B1C1D1,点A的坐标为(0,0,0),C1的坐标为(1,1,1),则线段AC1的中点坐标为__________.
【解析】结合中点坐标公式易得线段AC1的中点坐标为
答案: 5.在空间直角坐标系中,作出点M(6,-2,4).
【解析】点M的位置可按如下步骤作出:
先在x轴上作出横坐标是6的点M1,再将
M1沿与y轴平行的方向向左移动2个单位
得到点M2,然后将M2沿与z轴平行的方
向向上移动4个单位即得点M,M点的位置如图所示.一、选择题(每题4分,共16分)
1.在空间直角坐标系O-xyz中,点P(-2,0,3)位于( )
(A)xOz平面内 (B)yOz平面内
(C)y轴上 (D)z轴上
【解析】选A.∵点P(-2,0,3)的y坐标为零,
∴点P(-2,0,3)在xOz平面内.2.已知点A(-3,1,4),则点A关于原点的对称点的坐标为
( )
(A)(1,-3,-4) (B)(-4,1,-3)
(C)(3,-1,-4) (D)(4,-1,3)
【解析】选C.点A关于原点的对称点的坐标为(3,-1,-4).3.在空间直角坐标系中,已知点P(1,2,3),过P作平面xOy的垂线PQ,则垂足Q的坐标为( )
(A)(0,2,0) (B)(1,2,0)
(C)(1,0,3) (D)(0,2,3)
【解题提示】垂足Q的坐标,即为点P(1,2,3)在平面xOy内的射影.
【解析】选B.因为过P作平面xOy的垂线PQ,则垂足Q在xOy平面内,故满足z=0,x,y不变.故选B.4.以正方体ABCD-A1B1C1D1的棱AB、AD、AA1所在的直线为坐标轴建立空间直角坐标系,且正方体的棱长为一个单位长度,则棱CC1中点坐标为( )
(A)( ,1,1) (B)(1, ,1)
(C)(1,1, ) (D)( , ,1)
【解析】选C.由题可知点C(1,1,0),C1(1,1,1),
∴棱CC1中点坐标为(1,1, ).二、填空题(每题4分,共8分)
5.写出点P(2,3,4)在三条坐标轴上的射影的坐标_________,________,_________.
【解析】点P(2,3,4)在x,y,z轴上的射影的坐标分别为(2,0,0),(0,3,0),(0,0,4).
答案:(2,0,0) (0,3,0) (0,0,4)6.如图所示的
空间直角坐标系中,正方体棱长为2,
|PQ|=3|PR|,则点R的空间直角坐标
为__________.
【解题提示】充分借助平面几何的性质及条件|PQ|=
3|PR|求点R的坐标.【解析】过点R作RT⊥QT,如图所示,
由|PQ|=3|PR|及相似三角形的知识
可知
同理可求
∴点R的空间直角坐标为
答案: 【方法技巧】巧用平面几何的性质求空间点的坐标
立体几何是平面几何的拓展延伸,求解立体几何中的问题常常利用“降维”的思想,把立体几何问题平面化.如本题中巧用平行线的性质建立点T与点R坐标间的联系从而顺利写出所要求解的点的坐标.三、解答题(每题8分,共16分)
7.已知ABCD为平行四边形,且A(4,1,3),B(2,-5,1),C(3,7,-5),求点D的坐标.
【解题提示】利用平行四边形的对称性求点D的坐标.【解析】∵ABCD为平行四边形,且A(4,1,3),
C(3,7,-5),
∴线段AC的中点坐标为
设点D的坐标为(x,y,z),则对角线BD的中点坐标也为
解得
∴点D的坐标为(5,13,-3).8.如图,已知长方体ABCD-A′B′C′D′的边长为AB=12,AD=8,AA′=5.以这个长方体
的顶点A为坐标原点,射线AB,AD,AA′
分别为x轴、y轴、z轴的正半轴,建
立空间直角坐标系,求长方体各个
顶点的坐标.【解析】因为AB=12,AD=8,AA′=5,点A在坐标原点,即A(0,0,0),且B,D,A′分别在x轴、y轴、z轴上,所以它们的坐标分别为B(12,0,0),D(0,8,0),A′(0,0,5).
点C,B′,D′分别在xOy平面、xOz平面和yOz平面内,坐标分别为C(12,8,0),B′(12,0,5),D′(0,8,5).
点C′在三条坐标轴上的射影分别是点B,D,A′,故点C′的坐标为(12,8,5).【挑战能力】
(10分)(1)在空间直角坐标系O-xyz中,画出不共线的3个点A,B,C,使得这3个点的坐标都满足z=3,并画出图形;
(2)写出由这三个点确定的平面内的点的坐标应满足的条件.【解析】(1)取三个点A(0,0,3),C(4,0,3),B(0,4,3),其图形如图所示:
(2)A,B,C三点不共线,可以确定一
个平面,又因为这三点在xOy平面的同
侧,且到xOy平面的距离相等,所以平
面ABC平行于xOy平面,而且平面ABC内的每一个点在z轴上的射影到原点的距离都等于3,即该平面上的点的坐标都满足z=3.
