2.3.1-2.3.2 空间直角坐标系的建立和空间直角坐标系中点的坐标 课件2
文档属性
| 名称 | 2.3.1-2.3.2 空间直角坐标系的建立和空间直角坐标系中点的坐标 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 594.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-22 15:10:58 | ||
图片预览




文档简介
课件29张PPT。2.3.1 空间直角坐标系的建立
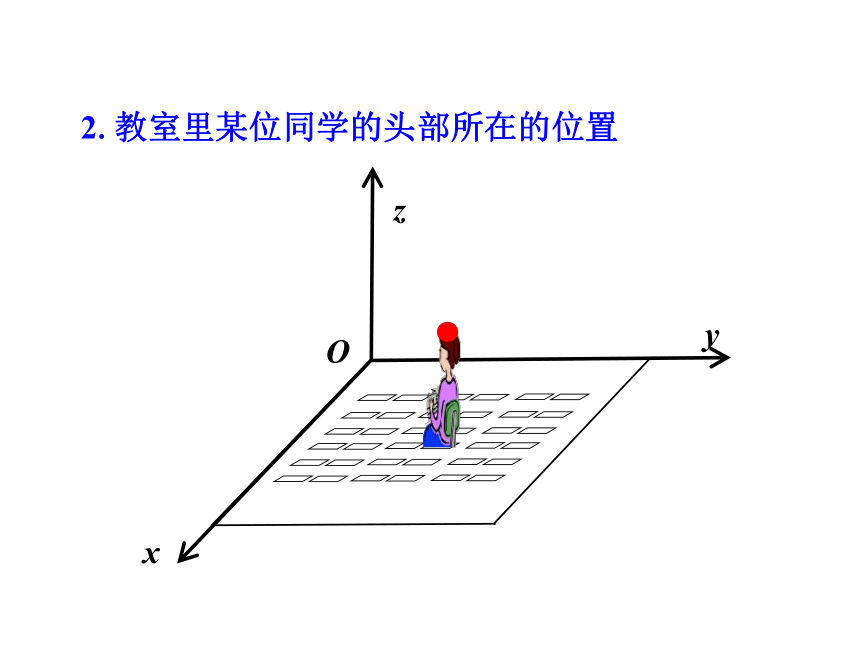
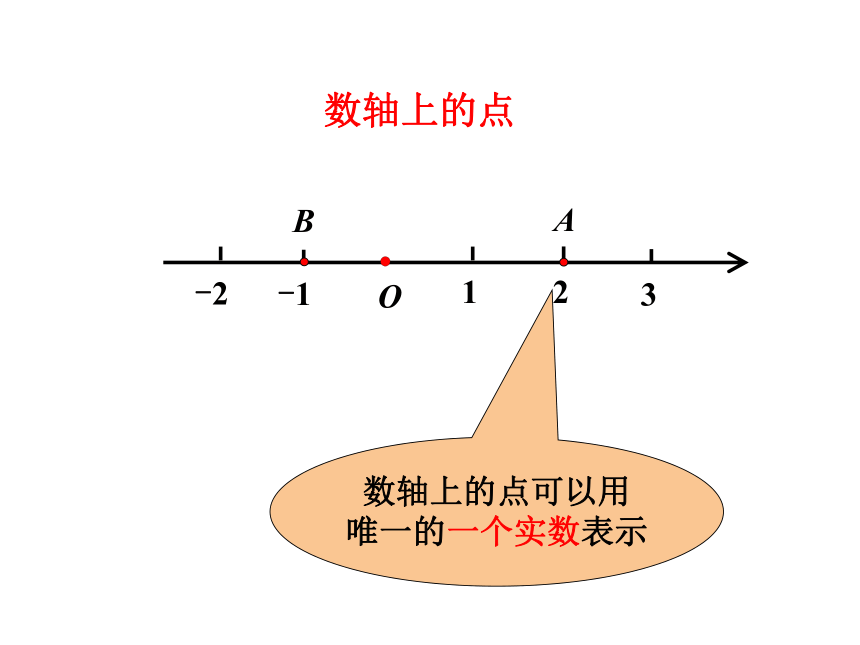
2.3.2 空间直角坐标系中点的坐标1.如何确定空中飞行的飞机的位置?yOx2.教室里某位同学的头部所在的位置zO数轴上的点可以用
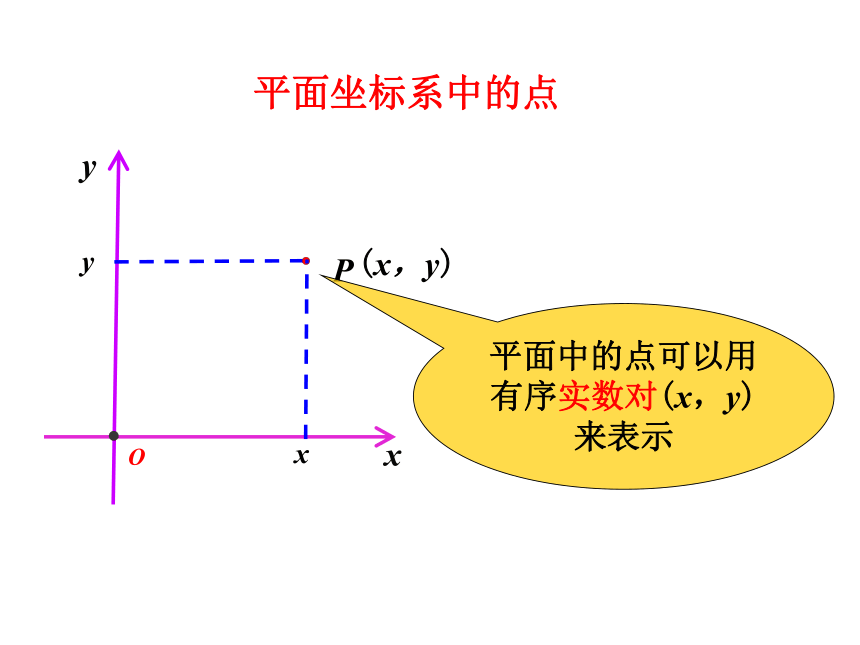
唯一的一个实数表示-1-2123AB数轴上的点xyPOxy(x,y)平面中的点可以用有序实数对(x,y)来表示平面坐标系中的点 在平面直角坐标系中, 平面上任意一点的位置,可以用坐标唯一表示. 那么空间中任意一点的位置,可以用坐标表示吗?怎样用坐标表示?请进入本节课的学习!1. 了解建立空间直角坐标系的背景. (重点)
2. 掌握建立空间直角坐标系的方法. (重点)
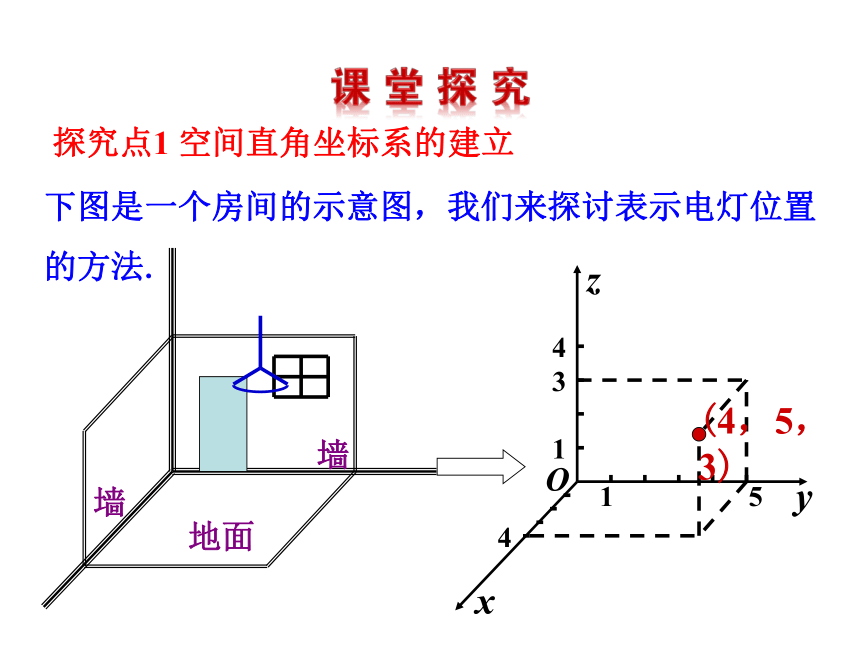
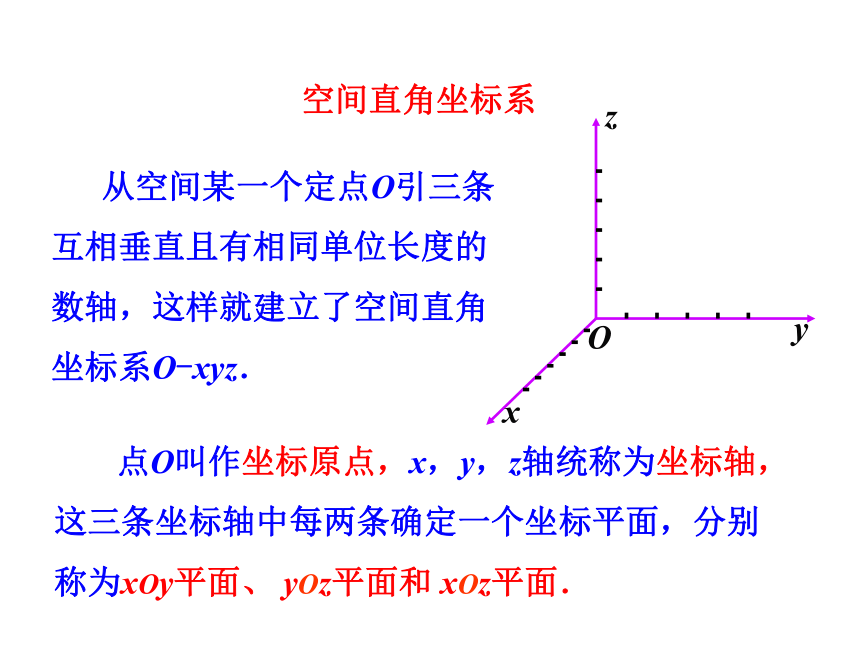
3. 会在空间直角坐标系中表示点的坐标. (难点)下图是一个房间的示意图,我们来探讨表示电灯位置的方法.(4,5,3)探究点1 空间直角坐标系的建立 从空间某一个定点O引三条互相垂直且有相同单位长度的数轴,这样就建立了空间直角坐标系O-xyz. 点O叫作坐标原点,x,y,z轴统称为坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xOy平面、 yOz平面和 xOz平面.空间直角坐标系右手系:伸出右手,让四指与大拇指垂直,并使四
指先指向x轴正方向,然后让四指沿握拳方向旋转
指向y轴正方向,此时大拇指的指向即为z轴正向.我们也称这样的坐标系为右手系.说明: ☆本书建立的坐标系
都是右手直角坐标系.思考1:有了空间直角坐标系,那空间中的任意一点A怎样来表示它的坐标呢?(a,b,c)探究点2 空间直角坐标系中点的坐标提示:经过A点作三个平面分别垂直于x轴、y轴和z轴,它们与x轴、y轴和z轴分别交于三点,三点在相应的坐标轴上的坐标a,b,c组成的有序实数对(a,b,c)叫作点A的坐标.记为A(a,b,c).面面面空间直角坐标系共有八个卦限xOy平面上的点竖坐标为0yOz平面上的点横坐标为0xOz平面上的点纵坐标为0x轴上的点纵坐标和竖坐标都为0z轴上的点横坐标和纵坐标都为0y轴上的点横坐标和竖坐标都为0一、坐标平面内的点二、坐标轴上的点?Oxyz111?A?D?C?B?E?F特殊位置的点的坐标【提升总结】思考2:在空间直角坐标系中,空间任意一点A与有序数组(x,y,z)有什么关系?
提示:在空间直角坐标系中,空间任意一点A与有序数组(x,y,z)之间是一种一一对应关系.
(1)过点A作三个平面分别垂直于x轴,y轴,z轴,它们与x轴,y轴,z轴分别交于点P,Q,R,点P,Q,R在相应数轴上的坐标依次为x,y,z.这样,对空间任意一点A,就定义了一个有序数组(x,y,z).(2)反之,对任意一个有序数组(x,y,z),按照上述作图的相反顺序,在坐标轴上分别作出点P,Q,R,使它们在x轴,y轴,z轴上的坐标分别是x,y,z,再分别过这些点作垂直于各自所在的坐标轴的平面,这三个平面的交点就是所求的点A.思考3:空间直角坐标系的建系不同,点的坐标相同吗?
提示:建立坐标系是解题的关键,坐标系建立的不同,点的坐标也不同,但点的相对位置是不变的,坐标系的不同也会引起解题过程的难易程度不同,因此解题时建立空间直角坐标系要慎重. 例1 如图点P′在x轴正半轴上,|OP′|=2,P′P
在xOz平面上,且垂直于x轴,|P′P|=1,求点P′
和P的坐标.解:点P′的坐标为(2,0,0),点P的坐标为(2,0,1)或(2,0,-1). 在长方体OABC-D′A′B′C′中, |OA|=3, |OC|=4, |OD′|=2,写出D′,A′,B′,C四点的坐标.【变式练习】例2.在空间直角坐标系中作出点P(3,-2,4).解:先确定点P′(3,-2,0)在xOy平面上的位置.因为点P的z坐标为4,
则|P′P|=4,且点P和z轴的正半轴在xOy平面的同侧,这样就确定了点P在空间直角坐标系中的位置,如图所示.例3.在同一个空间直角坐标系中画出下列各点:
A(0,0,0),B(3,0,0),C(3,2,0),
D(0,2,0),A′(0,0,1),B′(3,0,1),
C′(3,2,1),D′( 0,2,1).解:在空间直角坐标系中,画出以上各点,如图,它们刚好是一个长方体的八个顶点.在空间直角坐标系中描出下列各点.
A(0,1,1) B(0,0,2)
C(0,2,0) D(1,0,3)
E(2,2,0) F(1,0,0)解:在空间直角坐标系中,画出以上各点 如图:【变式练习】想一想? 在空间直角坐标系中, x轴上的点、xOy坐标平面内的点的坐标各有什么特点?1.x轴上的点横坐标就是与x轴交点的坐标,纵坐标和竖坐标都是0.2.xOy坐标平面内的点的竖坐标为0,横坐标与纵坐标分别是点向两轴作垂线交点的坐标.1.在空间直角坐标系中,点A(1,2,1)关于x轴对
称的点的坐标为( )
A.(-1,2,1) B.(-1,-2,1)
C.(1,-2,-1) D.(1,2,-1)C2.在空间直角坐标系中,点P(3,1,5)关于yOz平面
对称的点的坐标为( )
A.(-3,1,5) B.(-3,-1,-5)
C.(3,-1,-5) D.(-3,1,-5)A3.有下列叙述:
①在空间直角坐标系中,在x轴上的点的坐标一定可记为(0,b,c);
②在空间直角坐标系中,在y轴上的点的坐标一定可记为(0,b,0);
③在空间直角坐标系中,在xOy平面上的点的坐标一定可记为(a,0,c);
④在空间直角坐标系中,在yOz平面上的点的坐标一定可记为(0,b,c).
其中叙述正确的个数是________.24.如图,长方体OABC – D′A′B′C′中,|OA| = 3,|OC| = 4,|OD′| = 3,A′C′与B′D′相交于点P.分别写出点C,B′,P的坐标. 5.如图,棱长为3a的正方体OABC-DˊAˊBˊCˊ,点M在BˊCˊ上,且|CˊM|=2|MBˊ|,以O为坐标原点,建立如图空间直角坐标系,求点M的坐标. 解:由图形可知,M点在正方体的上
底面,所以M点的竖坐标与D′的竖坐标
相同,M在面BCC′B′上,得到点的
纵坐标为3a,因为 所以M点的横坐标是2a, 所以M点的坐标是(2a,3a,3a)1.空间直角坐标系的概念.
2.空间直角坐标系的画法.
3.运用空间直角坐标系表示空间点的坐标.
2.3.2 空间直角坐标系中点的坐标1.如何确定空中飞行的飞机的位置?yOx2.教室里某位同学的头部所在的位置zO数轴上的点可以用
唯一的一个实数表示-1-2123AB数轴上的点xyPOxy(x,y)平面中的点可以用有序实数对(x,y)来表示平面坐标系中的点 在平面直角坐标系中, 平面上任意一点的位置,可以用坐标唯一表示. 那么空间中任意一点的位置,可以用坐标表示吗?怎样用坐标表示?请进入本节课的学习!1. 了解建立空间直角坐标系的背景. (重点)
2. 掌握建立空间直角坐标系的方法. (重点)
3. 会在空间直角坐标系中表示点的坐标. (难点)下图是一个房间的示意图,我们来探讨表示电灯位置的方法.(4,5,3)探究点1 空间直角坐标系的建立 从空间某一个定点O引三条互相垂直且有相同单位长度的数轴,这样就建立了空间直角坐标系O-xyz. 点O叫作坐标原点,x,y,z轴统称为坐标轴,这三条坐标轴中每两条确定一个坐标平面,分别称为xOy平面、 yOz平面和 xOz平面.空间直角坐标系右手系:伸出右手,让四指与大拇指垂直,并使四
指先指向x轴正方向,然后让四指沿握拳方向旋转
指向y轴正方向,此时大拇指的指向即为z轴正向.我们也称这样的坐标系为右手系.说明: ☆本书建立的坐标系
都是右手直角坐标系.思考1:有了空间直角坐标系,那空间中的任意一点A怎样来表示它的坐标呢?(a,b,c)探究点2 空间直角坐标系中点的坐标提示:经过A点作三个平面分别垂直于x轴、y轴和z轴,它们与x轴、y轴和z轴分别交于三点,三点在相应的坐标轴上的坐标a,b,c组成的有序实数对(a,b,c)叫作点A的坐标.记为A(a,b,c).面面面空间直角坐标系共有八个卦限xOy平面上的点竖坐标为0yOz平面上的点横坐标为0xOz平面上的点纵坐标为0x轴上的点纵坐标和竖坐标都为0z轴上的点横坐标和纵坐标都为0y轴上的点横坐标和竖坐标都为0一、坐标平面内的点二、坐标轴上的点?Oxyz111?A?D?C?B?E?F特殊位置的点的坐标【提升总结】思考2:在空间直角坐标系中,空间任意一点A与有序数组(x,y,z)有什么关系?
提示:在空间直角坐标系中,空间任意一点A与有序数组(x,y,z)之间是一种一一对应关系.
(1)过点A作三个平面分别垂直于x轴,y轴,z轴,它们与x轴,y轴,z轴分别交于点P,Q,R,点P,Q,R在相应数轴上的坐标依次为x,y,z.这样,对空间任意一点A,就定义了一个有序数组(x,y,z).(2)反之,对任意一个有序数组(x,y,z),按照上述作图的相反顺序,在坐标轴上分别作出点P,Q,R,使它们在x轴,y轴,z轴上的坐标分别是x,y,z,再分别过这些点作垂直于各自所在的坐标轴的平面,这三个平面的交点就是所求的点A.思考3:空间直角坐标系的建系不同,点的坐标相同吗?
提示:建立坐标系是解题的关键,坐标系建立的不同,点的坐标也不同,但点的相对位置是不变的,坐标系的不同也会引起解题过程的难易程度不同,因此解题时建立空间直角坐标系要慎重. 例1 如图点P′在x轴正半轴上,|OP′|=2,P′P
在xOz平面上,且垂直于x轴,|P′P|=1,求点P′
和P的坐标.解:点P′的坐标为(2,0,0),点P的坐标为(2,0,1)或(2,0,-1). 在长方体OABC-D′A′B′C′中, |OA|=3, |OC|=4, |OD′|=2,写出D′,A′,B′,C四点的坐标.【变式练习】例2.在空间直角坐标系中作出点P(3,-2,4).解:先确定点P′(3,-2,0)在xOy平面上的位置.因为点P的z坐标为4,
则|P′P|=4,且点P和z轴的正半轴在xOy平面的同侧,这样就确定了点P在空间直角坐标系中的位置,如图所示.例3.在同一个空间直角坐标系中画出下列各点:
A(0,0,0),B(3,0,0),C(3,2,0),
D(0,2,0),A′(0,0,1),B′(3,0,1),
C′(3,2,1),D′( 0,2,1).解:在空间直角坐标系中,画出以上各点,如图,它们刚好是一个长方体的八个顶点.在空间直角坐标系中描出下列各点.
A(0,1,1) B(0,0,2)
C(0,2,0) D(1,0,3)
E(2,2,0) F(1,0,0)解:在空间直角坐标系中,画出以上各点 如图:【变式练习】想一想? 在空间直角坐标系中, x轴上的点、xOy坐标平面内的点的坐标各有什么特点?1.x轴上的点横坐标就是与x轴交点的坐标,纵坐标和竖坐标都是0.2.xOy坐标平面内的点的竖坐标为0,横坐标与纵坐标分别是点向两轴作垂线交点的坐标.1.在空间直角坐标系中,点A(1,2,1)关于x轴对
称的点的坐标为( )
A.(-1,2,1) B.(-1,-2,1)
C.(1,-2,-1) D.(1,2,-1)C2.在空间直角坐标系中,点P(3,1,5)关于yOz平面
对称的点的坐标为( )
A.(-3,1,5) B.(-3,-1,-5)
C.(3,-1,-5) D.(-3,1,-5)A3.有下列叙述:
①在空间直角坐标系中,在x轴上的点的坐标一定可记为(0,b,c);
②在空间直角坐标系中,在y轴上的点的坐标一定可记为(0,b,0);
③在空间直角坐标系中,在xOy平面上的点的坐标一定可记为(a,0,c);
④在空间直角坐标系中,在yOz平面上的点的坐标一定可记为(0,b,c).
其中叙述正确的个数是________.24.如图,长方体OABC – D′A′B′C′中,|OA| = 3,|OC| = 4,|OD′| = 3,A′C′与B′D′相交于点P.分别写出点C,B′,P的坐标. 5.如图,棱长为3a的正方体OABC-DˊAˊBˊCˊ,点M在BˊCˊ上,且|CˊM|=2|MBˊ|,以O为坐标原点,建立如图空间直角坐标系,求点M的坐标. 解:由图形可知,M点在正方体的上
底面,所以M点的竖坐标与D′的竖坐标
相同,M在面BCC′B′上,得到点的
纵坐标为3a,因为 所以M点的横坐标是2a, 所以M点的坐标是(2a,3a,3a)1.空间直角坐标系的概念.
2.空间直角坐标系的画法.
3.运用空间直角坐标系表示空间点的坐标.
