2.3.3 空间两点间的距离公式 课件1
文档属性
| 名称 | 2.3.3 空间两点间的距离公式 课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 605.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-22 00:00:00 | ||
图片预览








文档简介
课件52张PPT。2.3.3 空间两点间的距离公式 空间中两点间距离
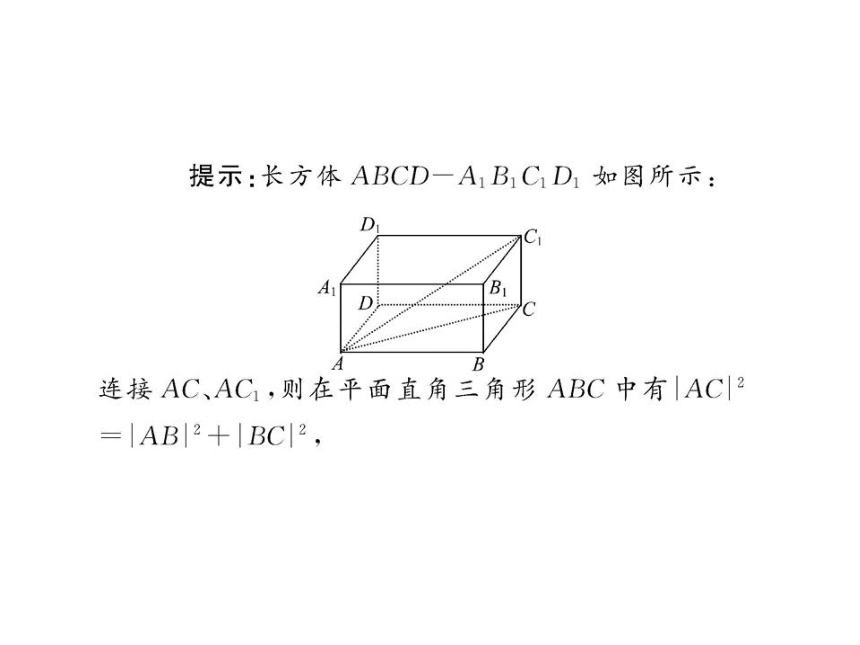
利用空间两点间的距离公式求空间两点间距离的步骤:
(1)建立适当的坐标系,并写出相关点的坐标;
(2)代入空间两点间的距离公式求值.
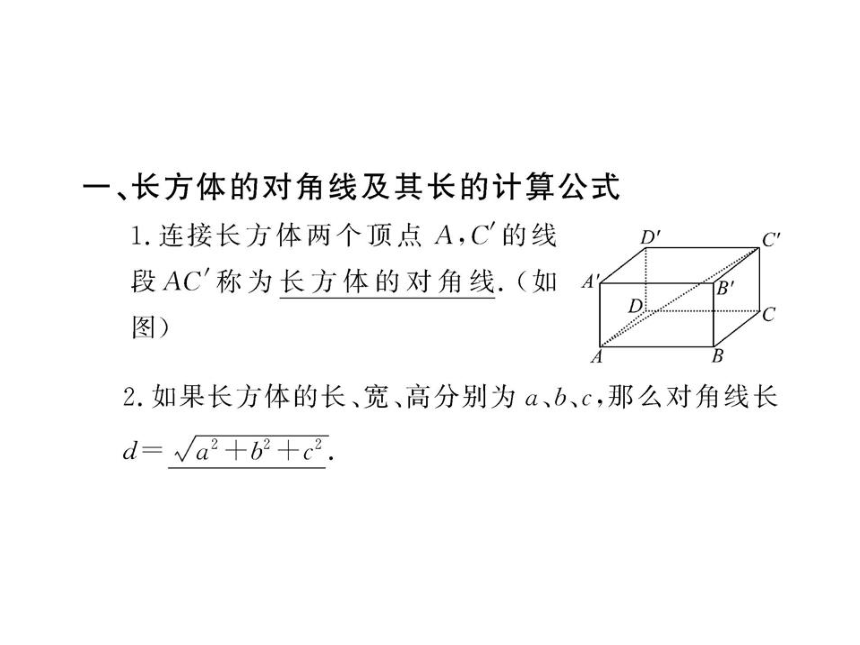
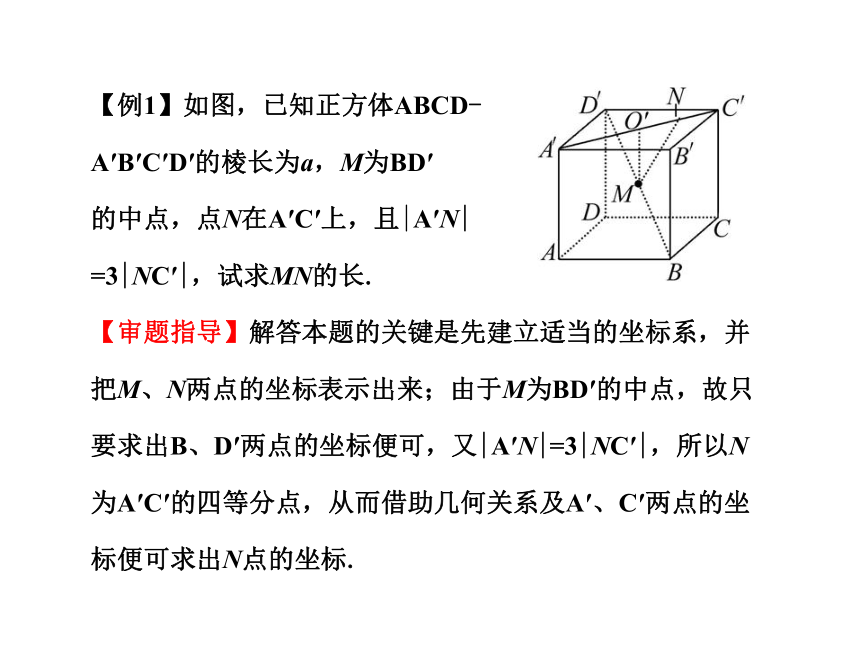
建系时尽量使较多的点落在坐标轴上.空间中两点间距离的计算 【例1】如图,已知正方体ABCD-
A′B′C′D′的棱长为a,M为BD′
的中点,点N在A′C′上,且|A′N|
=3|NC′|,试求MN的长.
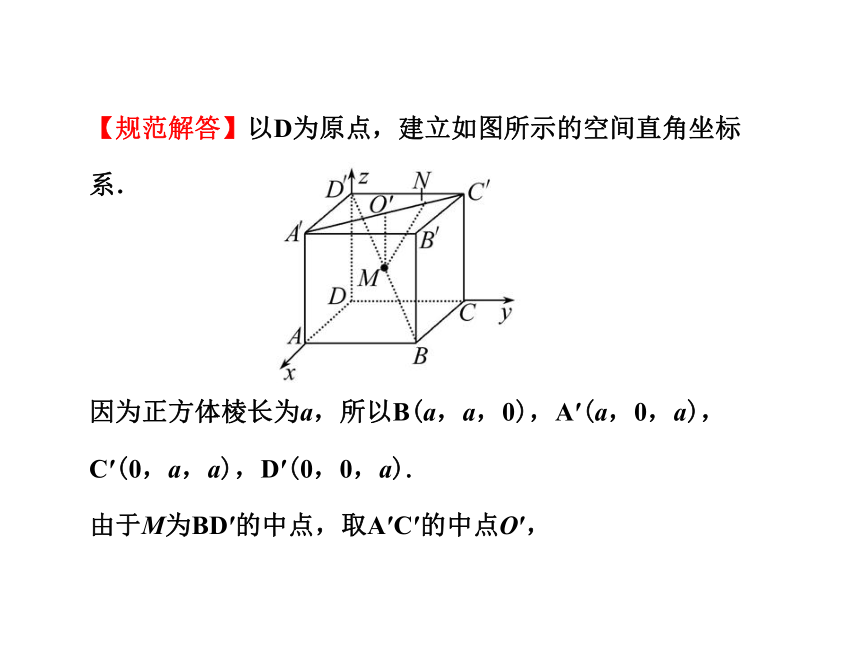
【审题指导】解答本题的关键是先建立适当的坐标系,并把M、N两点的坐标表示出来;由于M为BD′的中点,故只要求出B、D′两点的坐标便可,又|A′N|=3|NC′|,所以N为A′C′的四等分点,从而借助几何关系及A′、C′两点的坐标便可求出N点的坐标.【规范解答】以D为原点,建立如图所示的空间直角坐标系.
因为正方体棱长为a,所以B(a,a,0),A′(a,0,a),C′(0,a,a),D′(0,0,a).
由于M为BD′的中点,取A′C′的中点O′,所以
因为|A′N|=3|NC′|,所以N为A′C′的四等分点,从而N为O′C′的中点,故 根据空间两点距离公式,可得【互动探究】在题设不变的情况下,求正方体
ABCD-A′B′C′D′对角线的长.
【解析】∵正方体ABCD-A′B′C′D′对角线的长相等, 空间中两点间的距离公式
(1)空间中两点间的距离公式是数轴上和平面上两点间距离公式的进一步推广.①当空间中的任意两点P1,P2落在同一坐标平面内或与坐标平面平行的平面内时,此公式可转化为平面直角坐标系中的两点间的距离公式;②当空间中的任意两点P1,P2落在同一坐标轴上时,则该公式转化为数轴上两点间的距离公式.空间中两点间距离公式的应用(2)设P1(x1,y1,z1),P2(x2,y2,z2),公式
中x1,x2;y1,y2;z1,z2
的位置可互换.【例2】(1)在z轴上求一点使得它到点A(4,5,6)与到点B(-5,0,10)的距离相等;
(2)已知点P到坐标原点O的距离等于 且它的x坐标、y坐标、z坐标均相等,求该点的坐标.
【审题指导】(1)解答本题的关键是设出点的坐标为
P(0,0,z),利用|PB|=|PA|求z;
(2)利用 及x=y=z求解点的坐标.【规范解答】(1)由题意可知,设该点的坐标为
P(0,0,z),则
又|PA|=|PB|,所以z=6,
所以所求点的坐标为(0,0,6).(2)由题意可设P点的坐标为(x,y,z).
所以
又x=y=z,
所以
所以x=y=z=2或x=y=z=-2.
所以该点的坐标为(2,2,2)或(-2,-2,-2).【互动探究】若把本例中的(1)“在z轴上求一点”换成“在xOy平面内的直线2x-y=0上求一点”,其余条件不变,求相应问题.
【解析】设该点的坐标为(a,2a,0),则由题意可知
解得
∴该点的坐标为【例】方程(x-1)2+(y+2)2+(z-3)2=36表示什么样的几何图形?
【审题指导】类比空间两点间的距离公式及平面上圆的定义不难发现方程表示的轨迹图形.【规范解答】方程(x-1)2+(y+2)2+(z-3)2=36可化为:
其表示空间任意一点P(x,y,z)和定点(1,-2,3)的距离等于6.
因此方程表示空间上到定点(1,-2,3)的距离等于定长6的点的轨迹,即表示球心是(1,-2,3),半径为6的球面.【变式备选】(1)在空间中,到坐标原点的距离为1的点的轨迹是什么?写出其方程;
(2)求到两定点A(2,3,0),B(5,1,0)距离相等的点的坐标(x,y,z)满足的条件,并说明这样的点的集合构成什么图形;
(3)在坐标平面xOy内的点P到定点A(3,2,5),B(3,5,1)的距离相等,求点P的坐标满足的条件,并说明其轨迹是什么图形.【解析】(1)在空间中,到坐标原点的距离为1的点P(x,y,z)的轨迹是一个球面,满足|OP|=1,即
所以其轨迹方程是x2+y2+z2=1.
(2)由题意,得
整理,得6x-4y-13=0.
所以这样的点(x,y,z)满足的条件是6x-4y-13=0.
这样的点的集合是过线段AB的中点且与直线AB垂直的平面.(3)因为点P在xOy平面内,所以设点P(x,y,0),由题意,
得
化简,得
因为点P既在xOy平面内又在过线段AB的中点且与直线AB垂
直的平面内,所以点P的轨迹是两个平面的交线,即xOy平
面内的直线 【典例】(12分)如图,在棱长为1的正方体ABCD-A1B1C1D1中,以正方体的三条棱所在直线为轴建立空间直角坐标系O-xyz.
(1)若点P在线段BD1上,且满足3|BP|=|BD1|,试写出点P的坐标,并写出P关于y轴的对称点P′的坐标;
(2)在线段C1D上找一点M,使得点M到点
P的距离最小,求出点M的坐标.【审题指导】(1)借助3|BP|=|BD1|及平面几何的知识求点P的坐标,利用对称关系求点P′的坐标;
(2)利用空间两点间的距离公式建立点M到点P的距离的函数,并用函数的思想求其最小值,及此时的点M的坐标.【规范解答】(1)由题意知P的坐标为
………………………………………………………………2分
P关于y轴的对称点P′的坐标为 …………5分
(2)设线段C1D上一点M的坐标为(0,m,m),则有
当 时|MP|取到最小值,
所以点M为 ………………………… 12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】在空间直角坐标系中,z轴上的点与(1,2,3)距离的最小值是___________.
【解题提示】利用空间两点间的距离公式建立z轴上的点与点(1,2,3)的距离的函数,并用函数的思想求其最小值.
【解析】设z轴上的点为(0,0,z),
则距离
答案: 1.在空间直角坐标系中,点C(1,-1,-2)到坐标系原点O的距离是( )
(A)1 (B)2
【解析】选C. 2.点B是点A(-1,2,3)在坐标平面yOz内的射影,则|AB|等于( )
(C)1 (D)3【解析】选C.方法一:∵点A(-1,2,3)在坐标平面yOz内的射影B的坐标为(0,2,3),
方法二:∵点B是点A(-1,2,3)在坐标平面yOz内的射影,∴|AB|=|-1-0|=1.故选C.3.坐标原点到下列各点的距离最小的是( )
(A)E(1,1,1) (B)F(1,2,2)
(C)G(2,-3,5) (D)H(3,0,4)
【解析】选A.由两点间的距离公式可得,
|OF|=3, |OH|=5.显然|OE|最小.4.在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是__________.
【解析】设M(0,y,0),由12+y2+4=12+(-3-y)2+12可得y=-1,故M(0,-1,0).
答案:(0,-1,0)5.已知A(1,-2,11),B(4,2,3),C(6,-1,4),求证:△ABC为直角三角形.
【证明】
同理可求
∴|AC|2+|BC|2=|AB|2.
∴△ABC为直角三角形.一、选择题(每题4分,共16分)
1.已知A(1,2,3),B(3,3,m), C(0,-1,0),D(2,-1,-1),则( )
(A)|AB|>|CD|
(B)|AB|<|CD|
(C)|AB|≤|CD|
(D)|AB|≥|CD|【解析】选D.由两点间的距离公式可得
所以|AB|≥|CD|.2.已知△ABC的三个顶点A(3,3,2),B(4,-3,7),C(0,5,1),则BC边上的中线长为( )
(A)2 (B)3 (C)4 (D)5
【解析】选B.由题意可知BC的中点D坐标为(2,1,4),
又A(3,3,2)3.已知A(-4,2,3)关于xOz平面的对称点为A1,A1关于z轴的对称点为A2,则|AA2|等于( )
(A)8 (B)12 (C)16 (D)19
【解析】选A.A1点的坐标为(-4,-2,3),A2点的坐标为(4,2,3).
∴|AA2|=8.4.在空间直角坐标系中,一定点到三个坐标平面的距离都是1,则该点到原点的距离是( )
(A) (B) (C)1 (D)3
【解题提示】利用该定点到三个坐标平面的距离都是1求出点的坐标,然后用空间两点间的距离公式求解.
【解析】选B.一定点到三个坐标平面的距离都是1,则该点的坐标可为(1,1,1)
∴该点到原点的距离为二、填空题(每题4分,共8分)
5.已知长方体的长宽高分别为3,4,5.则该长方体的对角线长为__________.
【解析】该长方体的对角线长为
答案:6.已知A(3,5,-7)和点B(-2,4,3),则线段AB在坐标平面yOz上的射影长度为__________.
【解析】点A(3,5,-7)、B(-2,4,3)在坐标平面yOz上的射影分别为A′(0,5,-7)、B′(0,4,3).
答案: 【误区警示】本题在求解过程中常因不理解“线段AB在坐标平面yOz上的射影长度”而出现计算错误.三、解答题(每题8分,共16分)
7.已知M(x,2,3)、N(5,4,7)且|MN|=6,求x的值.
【解析】∵|MN|=6,
即(x-5)2=16,解得x=1或x=9.
∴x=1或x=9.8.如图,在空间直角坐标系中BC=2,原
点O是BC的中点,点A的坐标是
点D在平面yOz上,且∠BDC=90°,
∠DCB=30°,求点D到AD中点的距离.
【解题提示】利用直角三角形的知识求点D的坐标,
由点A的坐标是 及点D的坐标求AD中点的坐标,进
而可求得点D到AD中点的距离.【解析】因点D在平面yOz上,可设点D的坐标为(0,y,z),在Rt△BCD中BC=2且∠BDC=90°,∠DCB=30°,
则
∴点D的坐标为
∵点A的坐标是
∴AD中点的坐标为
∴点D到AD中点的距离为【挑战能力】
(10分)在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问
(1)在y轴上是否存在点M,满足|MA|=|MB|?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M的坐标.【解析】(1)假设在y轴上存在点M,满足|MA|=|MB|.
∵M在y轴上,设M(0,y,0),由|MA|=|MB|,得
显然此式对任意y∈R恒成立.
即y轴上所有点都满足关系|MA|=|MB|.(2)假设在y轴上存在点M,使△MAB为等边三角形.
由(1)可知,y轴上任意一点都有|MA|=|MB|,所以只要|MA|=|AB|就可以使得△MAB是等边三角形.
解得
故y轴上存在M点使△MAB为等边三角形,
M坐标为 【方法技巧】探索性问题的解法
对该类问题的解题要诀有:(1)试:阅读题意,分清条件和结论,尝试最简单、最基础的运算.(2)猜:在前面尝试的基础上,大胆猜想,可以运用归纳、类比、推广、化归等思想方法多角度、多维度地猜想,合理进行猜想是关键的一步.(3)证:综合运用数学知识进行求解与证明,要注意前后联系,过程严谨.在探索开放题的解答过程中,要注意尝试举例,并进行多方位的联想,将式子结构、运算法则、解题方法、问题的结论等引申、推广或迁移,从而进行大胆的猜想,最后再进行规范地证明.
利用空间两点间的距离公式求空间两点间距离的步骤:
(1)建立适当的坐标系,并写出相关点的坐标;
(2)代入空间两点间的距离公式求值.
建系时尽量使较多的点落在坐标轴上.空间中两点间距离的计算 【例1】如图,已知正方体ABCD-
A′B′C′D′的棱长为a,M为BD′
的中点,点N在A′C′上,且|A′N|
=3|NC′|,试求MN的长.
【审题指导】解答本题的关键是先建立适当的坐标系,并把M、N两点的坐标表示出来;由于M为BD′的中点,故只要求出B、D′两点的坐标便可,又|A′N|=3|NC′|,所以N为A′C′的四等分点,从而借助几何关系及A′、C′两点的坐标便可求出N点的坐标.【规范解答】以D为原点,建立如图所示的空间直角坐标系.
因为正方体棱长为a,所以B(a,a,0),A′(a,0,a),C′(0,a,a),D′(0,0,a).
由于M为BD′的中点,取A′C′的中点O′,所以
因为|A′N|=3|NC′|,所以N为A′C′的四等分点,从而N为O′C′的中点,故 根据空间两点距离公式,可得【互动探究】在题设不变的情况下,求正方体
ABCD-A′B′C′D′对角线的长.
【解析】∵正方体ABCD-A′B′C′D′对角线的长相等, 空间中两点间的距离公式
(1)空间中两点间的距离公式是数轴上和平面上两点间距离公式的进一步推广.①当空间中的任意两点P1,P2落在同一坐标平面内或与坐标平面平行的平面内时,此公式可转化为平面直角坐标系中的两点间的距离公式;②当空间中的任意两点P1,P2落在同一坐标轴上时,则该公式转化为数轴上两点间的距离公式.空间中两点间距离公式的应用(2)设P1(x1,y1,z1),P2(x2,y2,z2),公式
中x1,x2;y1,y2;z1,z2
的位置可互换.【例2】(1)在z轴上求一点使得它到点A(4,5,6)与到点B(-5,0,10)的距离相等;
(2)已知点P到坐标原点O的距离等于 且它的x坐标、y坐标、z坐标均相等,求该点的坐标.
【审题指导】(1)解答本题的关键是设出点的坐标为
P(0,0,z),利用|PB|=|PA|求z;
(2)利用 及x=y=z求解点的坐标.【规范解答】(1)由题意可知,设该点的坐标为
P(0,0,z),则
又|PA|=|PB|,所以z=6,
所以所求点的坐标为(0,0,6).(2)由题意可设P点的坐标为(x,y,z).
所以
又x=y=z,
所以
所以x=y=z=2或x=y=z=-2.
所以该点的坐标为(2,2,2)或(-2,-2,-2).【互动探究】若把本例中的(1)“在z轴上求一点”换成“在xOy平面内的直线2x-y=0上求一点”,其余条件不变,求相应问题.
【解析】设该点的坐标为(a,2a,0),则由题意可知
解得
∴该点的坐标为【例】方程(x-1)2+(y+2)2+(z-3)2=36表示什么样的几何图形?
【审题指导】类比空间两点间的距离公式及平面上圆的定义不难发现方程表示的轨迹图形.【规范解答】方程(x-1)2+(y+2)2+(z-3)2=36可化为:
其表示空间任意一点P(x,y,z)和定点(1,-2,3)的距离等于6.
因此方程表示空间上到定点(1,-2,3)的距离等于定长6的点的轨迹,即表示球心是(1,-2,3),半径为6的球面.【变式备选】(1)在空间中,到坐标原点的距离为1的点的轨迹是什么?写出其方程;
(2)求到两定点A(2,3,0),B(5,1,0)距离相等的点的坐标(x,y,z)满足的条件,并说明这样的点的集合构成什么图形;
(3)在坐标平面xOy内的点P到定点A(3,2,5),B(3,5,1)的距离相等,求点P的坐标满足的条件,并说明其轨迹是什么图形.【解析】(1)在空间中,到坐标原点的距离为1的点P(x,y,z)的轨迹是一个球面,满足|OP|=1,即
所以其轨迹方程是x2+y2+z2=1.
(2)由题意,得
整理,得6x-4y-13=0.
所以这样的点(x,y,z)满足的条件是6x-4y-13=0.
这样的点的集合是过线段AB的中点且与直线AB垂直的平面.(3)因为点P在xOy平面内,所以设点P(x,y,0),由题意,
得
化简,得
因为点P既在xOy平面内又在过线段AB的中点且与直线AB垂
直的平面内,所以点P的轨迹是两个平面的交线,即xOy平
面内的直线 【典例】(12分)如图,在棱长为1的正方体ABCD-A1B1C1D1中,以正方体的三条棱所在直线为轴建立空间直角坐标系O-xyz.
(1)若点P在线段BD1上,且满足3|BP|=|BD1|,试写出点P的坐标,并写出P关于y轴的对称点P′的坐标;
(2)在线段C1D上找一点M,使得点M到点
P的距离最小,求出点M的坐标.【审题指导】(1)借助3|BP|=|BD1|及平面几何的知识求点P的坐标,利用对称关系求点P′的坐标;
(2)利用空间两点间的距离公式建立点M到点P的距离的函数,并用函数的思想求其最小值,及此时的点M的坐标.【规范解答】(1)由题意知P的坐标为
………………………………………………………………2分
P关于y轴的对称点P′的坐标为 …………5分
(2)设线段C1D上一点M的坐标为(0,m,m),则有
当 时|MP|取到最小值,
所以点M为 ………………………… 12分【误区警示】对解答本题时易犯的错误具体分析如下:【即时训练】在空间直角坐标系中,z轴上的点与(1,2,3)距离的最小值是___________.
【解题提示】利用空间两点间的距离公式建立z轴上的点与点(1,2,3)的距离的函数,并用函数的思想求其最小值.
【解析】设z轴上的点为(0,0,z),
则距离
答案: 1.在空间直角坐标系中,点C(1,-1,-2)到坐标系原点O的距离是( )
(A)1 (B)2
【解析】选C. 2.点B是点A(-1,2,3)在坐标平面yOz内的射影,则|AB|等于( )
(C)1 (D)3【解析】选C.方法一:∵点A(-1,2,3)在坐标平面yOz内的射影B的坐标为(0,2,3),
方法二:∵点B是点A(-1,2,3)在坐标平面yOz内的射影,∴|AB|=|-1-0|=1.故选C.3.坐标原点到下列各点的距离最小的是( )
(A)E(1,1,1) (B)F(1,2,2)
(C)G(2,-3,5) (D)H(3,0,4)
【解析】选A.由两点间的距离公式可得,
|OF|=3, |OH|=5.显然|OE|最小.4.在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是__________.
【解析】设M(0,y,0),由12+y2+4=12+(-3-y)2+12可得y=-1,故M(0,-1,0).
答案:(0,-1,0)5.已知A(1,-2,11),B(4,2,3),C(6,-1,4),求证:△ABC为直角三角形.
【证明】
同理可求
∴|AC|2+|BC|2=|AB|2.
∴△ABC为直角三角形.一、选择题(每题4分,共16分)
1.已知A(1,2,3),B(3,3,m), C(0,-1,0),D(2,-1,-1),则( )
(A)|AB|>|CD|
(B)|AB|<|CD|
(C)|AB|≤|CD|
(D)|AB|≥|CD|【解析】选D.由两点间的距离公式可得
所以|AB|≥|CD|.2.已知△ABC的三个顶点A(3,3,2),B(4,-3,7),C(0,5,1),则BC边上的中线长为( )
(A)2 (B)3 (C)4 (D)5
【解析】选B.由题意可知BC的中点D坐标为(2,1,4),
又A(3,3,2)3.已知A(-4,2,3)关于xOz平面的对称点为A1,A1关于z轴的对称点为A2,则|AA2|等于( )
(A)8 (B)12 (C)16 (D)19
【解析】选A.A1点的坐标为(-4,-2,3),A2点的坐标为(4,2,3).
∴|AA2|=8.4.在空间直角坐标系中,一定点到三个坐标平面的距离都是1,则该点到原点的距离是( )
(A) (B) (C)1 (D)3
【解题提示】利用该定点到三个坐标平面的距离都是1求出点的坐标,然后用空间两点间的距离公式求解.
【解析】选B.一定点到三个坐标平面的距离都是1,则该点的坐标可为(1,1,1)
∴该点到原点的距离为二、填空题(每题4分,共8分)
5.已知长方体的长宽高分别为3,4,5.则该长方体的对角线长为__________.
【解析】该长方体的对角线长为
答案:6.已知A(3,5,-7)和点B(-2,4,3),则线段AB在坐标平面yOz上的射影长度为__________.
【解析】点A(3,5,-7)、B(-2,4,3)在坐标平面yOz上的射影分别为A′(0,5,-7)、B′(0,4,3).
答案: 【误区警示】本题在求解过程中常因不理解“线段AB在坐标平面yOz上的射影长度”而出现计算错误.三、解答题(每题8分,共16分)
7.已知M(x,2,3)、N(5,4,7)且|MN|=6,求x的值.
【解析】∵|MN|=6,
即(x-5)2=16,解得x=1或x=9.
∴x=1或x=9.8.如图,在空间直角坐标系中BC=2,原
点O是BC的中点,点A的坐标是
点D在平面yOz上,且∠BDC=90°,
∠DCB=30°,求点D到AD中点的距离.
【解题提示】利用直角三角形的知识求点D的坐标,
由点A的坐标是 及点D的坐标求AD中点的坐标,进
而可求得点D到AD中点的距离.【解析】因点D在平面yOz上,可设点D的坐标为(0,y,z),在Rt△BCD中BC=2且∠BDC=90°,∠DCB=30°,
则
∴点D的坐标为
∵点A的坐标是
∴AD中点的坐标为
∴点D到AD中点的距离为【挑战能力】
(10分)在空间直角坐标系中,已知A(3,0,1)和B(1,0,-3),试问
(1)在y轴上是否存在点M,满足|MA|=|MB|?
(2)在y轴上是否存在点M,使△MAB为等边三角形?若存在,试求出点M的坐标.【解析】(1)假设在y轴上存在点M,满足|MA|=|MB|.
∵M在y轴上,设M(0,y,0),由|MA|=|MB|,得
显然此式对任意y∈R恒成立.
即y轴上所有点都满足关系|MA|=|MB|.(2)假设在y轴上存在点M,使△MAB为等边三角形.
由(1)可知,y轴上任意一点都有|MA|=|MB|,所以只要|MA|=|AB|就可以使得△MAB是等边三角形.
解得
故y轴上存在M点使△MAB为等边三角形,
M坐标为 【方法技巧】探索性问题的解法
对该类问题的解题要诀有:(1)试:阅读题意,分清条件和结论,尝试最简单、最基础的运算.(2)猜:在前面尝试的基础上,大胆猜想,可以运用归纳、类比、推广、化归等思想方法多角度、多维度地猜想,合理进行猜想是关键的一步.(3)证:综合运用数学知识进行求解与证明,要注意前后联系,过程严谨.在探索开放题的解答过程中,要注意尝试举例,并进行多方位的联想,将式子结构、运算法则、解题方法、问题的结论等引申、推广或迁移,从而进行大胆的猜想,最后再进行规范地证明.
