2.3.3 空间两点间的距离公式 课件2
文档属性
| 名称 | 2.3.3 空间两点间的距离公式 课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 343.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-22 14:56:38 | ||
图片预览




文档简介
课件18张PPT。2.3.3 空间两点间的距离公式 建筑用砖通常是长方体,我们可以拿尺子测量出一块砖的长、宽和高,那么怎样测量它的对角线AC′的长度呢?直接测量比较困难,我们可以用间接的方法去测量.如果有三块砖,你如何测量AC′的长度,两块呢?1.掌握空间两点间的距离公式. (重点)
2.会应用距离公式解决有关问题.(难点)
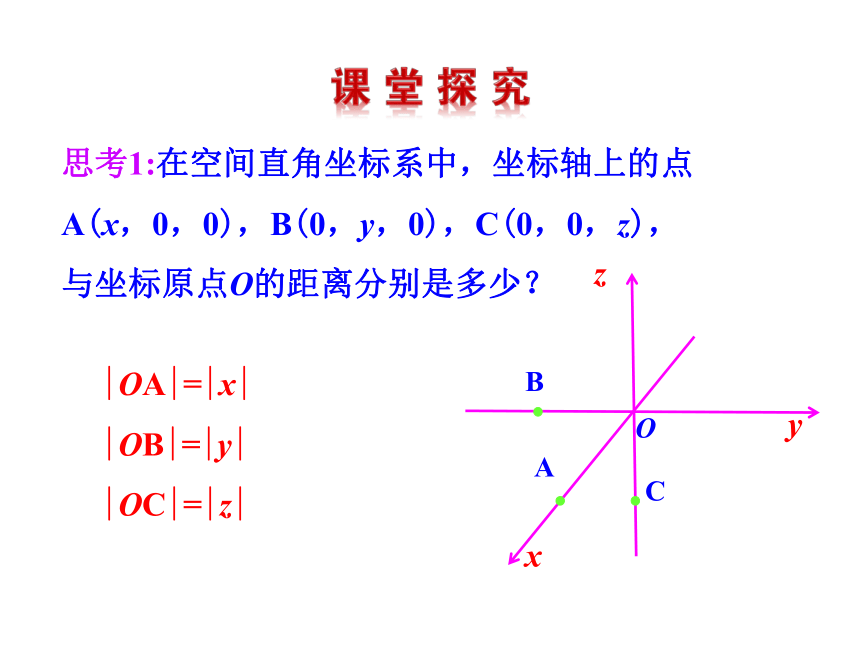
3.通过对空间两点间距离公式的探究与推导,初步意识到将空间问题转化为平面问题是解决空间问题的基本思想方法. 思考1:在空间直角坐标系中,坐标轴上的点
A(x,0,0),B(0,y,0),C(0,0,z),
与坐标原点O的距离分别是多少?|OA|=|x|
|OB|=|y|
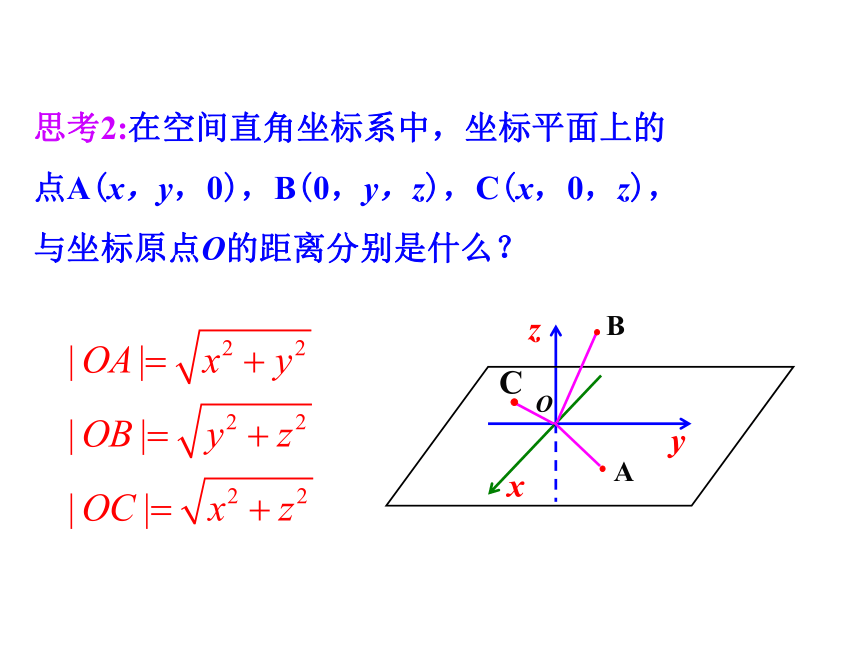
|OC|=|z|思考2:在空间直角坐标系中,坐标平面上的
点A(x,y,0),B(0,y,z),C(x,0,z),
与坐标原点O的距离分别是什么?思考3:在空间直角坐标系中,设点 P(x,y,z)
在xOy平面上的射影为M,则点M的坐标是什么?
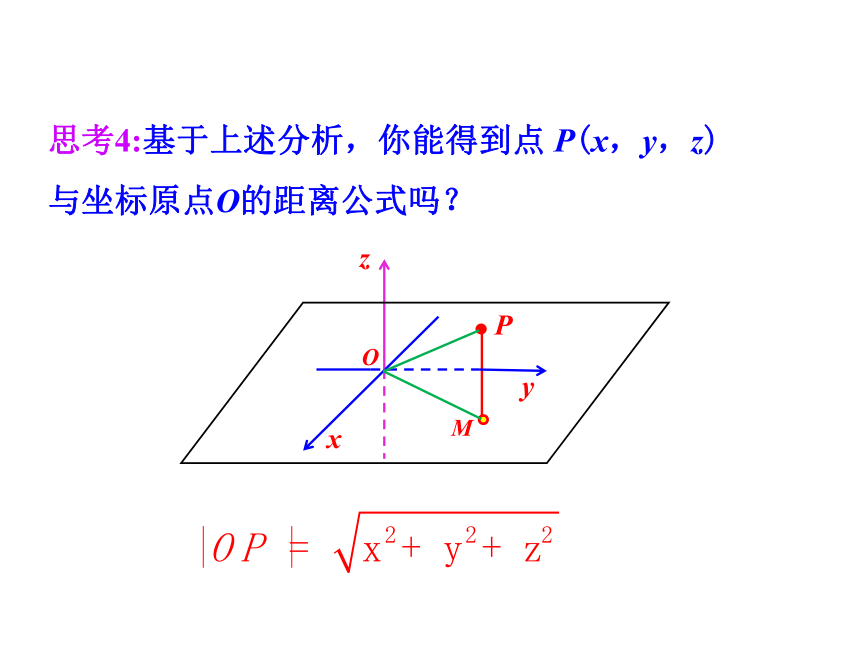
|PM|,|OM|的值分别是什么?思考4:基于上述分析,你能得到点 P(x,y,z)
与坐标原点O的距离公式吗?在空间中,到定点的距离
等于定长的点的轨迹是以原点为球心,
半径长为 r 的球面. 探究思考5:如果是空间中任意一点到点之间的距离公式会是怎样呢?如图,设是空间中任意两点,且在xOy平面上的射影分别
为M,N,那么M,N的坐标为在xOy平面上,过点作 的垂线,垂足为H,则所以因此,空间中任意两点之间的距离所以点P的坐标为(9,0,0)或(-1,0,0).解:设点P的坐标是(x,0,0),由题意, 所以(x-4)2=25.解得x=9或x=-1..PP0.解:求下列两点的距离【变式练习】例2. 在xOy平面内的直线x+y=1上确定一点M,使M到点N(6,5,1)的距离最小.解:由已知,可设M(x,1-x,0),则 在z轴上求一点M,使点M到点A(1,0,2)与点B(1,
-3,1)的距离相等.解:设M(0,0,z),根据题意:|MA|2=|MB|2,
故12+02+(z-2)2 =12+(-3)2+(z-1)2
解得z=-3,故M(0,0,-3).【变式练习】A2.已知空间两点P(-1,2,-3),Q(3,-2,-1),则P,Q两点间的距离为( )
A.6 B.2 C.36 D.4A3.在空间直角坐标系中,A(1,-3,0),Q(2,0,4)之间的距离是 . 25.已知三角形的三个顶点A(1,5,2),B(2,3,4),C(3,1,5),求:三角形三边的边长.解:1.已知点写出其空间直角坐标.
2.空间直角坐标系中的距离公式.
3.空间直角坐标系中的距离公式的应用.
2.会应用距离公式解决有关问题.(难点)
3.通过对空间两点间距离公式的探究与推导,初步意识到将空间问题转化为平面问题是解决空间问题的基本思想方法. 思考1:在空间直角坐标系中,坐标轴上的点
A(x,0,0),B(0,y,0),C(0,0,z),
与坐标原点O的距离分别是多少?|OA|=|x|
|OB|=|y|
|OC|=|z|思考2:在空间直角坐标系中,坐标平面上的
点A(x,y,0),B(0,y,z),C(x,0,z),
与坐标原点O的距离分别是什么?思考3:在空间直角坐标系中,设点 P(x,y,z)
在xOy平面上的射影为M,则点M的坐标是什么?
|PM|,|OM|的值分别是什么?思考4:基于上述分析,你能得到点 P(x,y,z)
与坐标原点O的距离公式吗?在空间中,到定点的距离
等于定长的点的轨迹是以原点为球心,
半径长为 r 的球面. 探究思考5:如果是空间中任意一点到点之间的距离公式会是怎样呢?如图,设是空间中任意两点,且在xOy平面上的射影分别
为M,N,那么M,N的坐标为在xOy平面上,过点作 的垂线,垂足为H,则所以因此,空间中任意两点之间的距离所以点P的坐标为(9,0,0)或(-1,0,0).解:设点P的坐标是(x,0,0),由题意, 所以(x-4)2=25.解得x=9或x=-1..PP0.解:求下列两点的距离【变式练习】例2. 在xOy平面内的直线x+y=1上确定一点M,使M到点N(6,5,1)的距离最小.解:由已知,可设M(x,1-x,0),则 在z轴上求一点M,使点M到点A(1,0,2)与点B(1,
-3,1)的距离相等.解:设M(0,0,z),根据题意:|MA|2=|MB|2,
故12+02+(z-2)2 =12+(-3)2+(z-1)2
解得z=-3,故M(0,0,-3).【变式练习】A2.已知空间两点P(-1,2,-3),Q(3,-2,-1),则P,Q两点间的距离为( )
A.6 B.2 C.36 D.4A3.在空间直角坐标系中,A(1,-3,0),Q(2,0,4)之间的距离是 . 25.已知三角形的三个顶点A(1,5,2),B(2,3,4),C(3,1,5),求:三角形三边的边长.解:1.已知点写出其空间直角坐标.
2.空间直角坐标系中的距离公式.
3.空间直角坐标系中的距离公式的应用.
