大题精做 2016-2017学年高一数学人教A版必修2(第01-02章)第一章 空间几何体 大题精做3 1.3空间几何体的表面积与体积 Word版含解析
文档属性
| 名称 | 大题精做 2016-2017学年高一数学人教A版必修2(第01-02章)第一章 空间几何体 大题精做3 1.3空间几何体的表面积与体积 Word版含解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 405.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览


文档简介
大题精做3
1.3空间几何体的表面积与体积
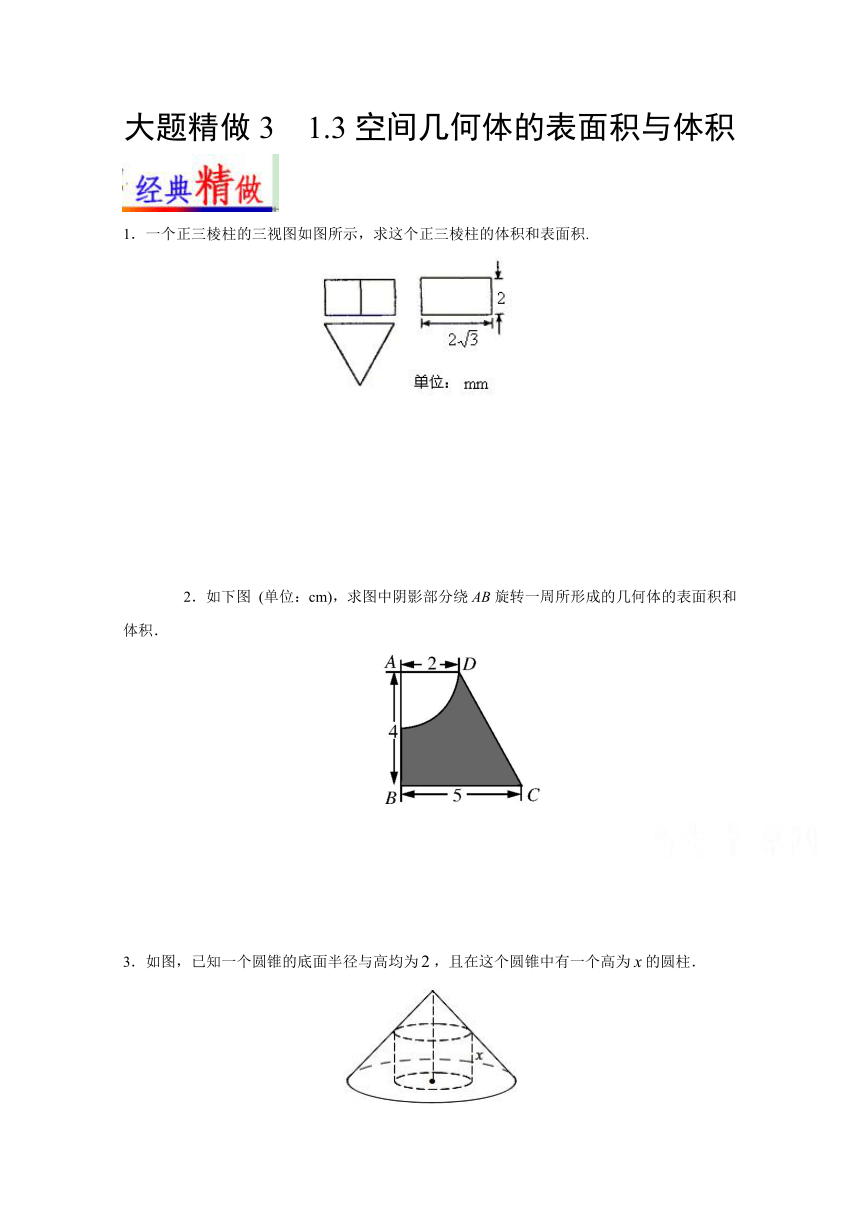
1.一个正三棱柱的三视图如图所示,求这个正三棱柱的体积和表面积.
( http: / / www.21cnjy.com )
2.如下图
(单位:cm),求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积.
( http: / / www.21cnjy.com )
3.如图,已知一个圆锥的底面半径与高均为,且在这个圆锥中有一个高为的圆柱.
( http: / / www.21cnjy.com )
(1)用表示此圆柱的侧面积表达式;
(2)当此圆柱的侧面积最大时,求此圆柱的体积.
4.一个倒圆锥形容器,它的轴截面是正三角形.
(1)如果正三角形的边长为2,求圆锥形容器的体积;
(2)如果在容器内放一个半径为r的铁球(
( http: / / www.21cnjy.com )铁球完全在容器内),并向容器内注水,使水面漫过铁球且恰好与铁球相切(如图所示),则将铁球取出后,容器内的水深是多少
( http: / / www.21cnjy.com )
5.已知某几何体的俯视图是如图所示的矩形.正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
(1)判断该几何体的形状;
(2)求该几何体的体积V与侧面积S.
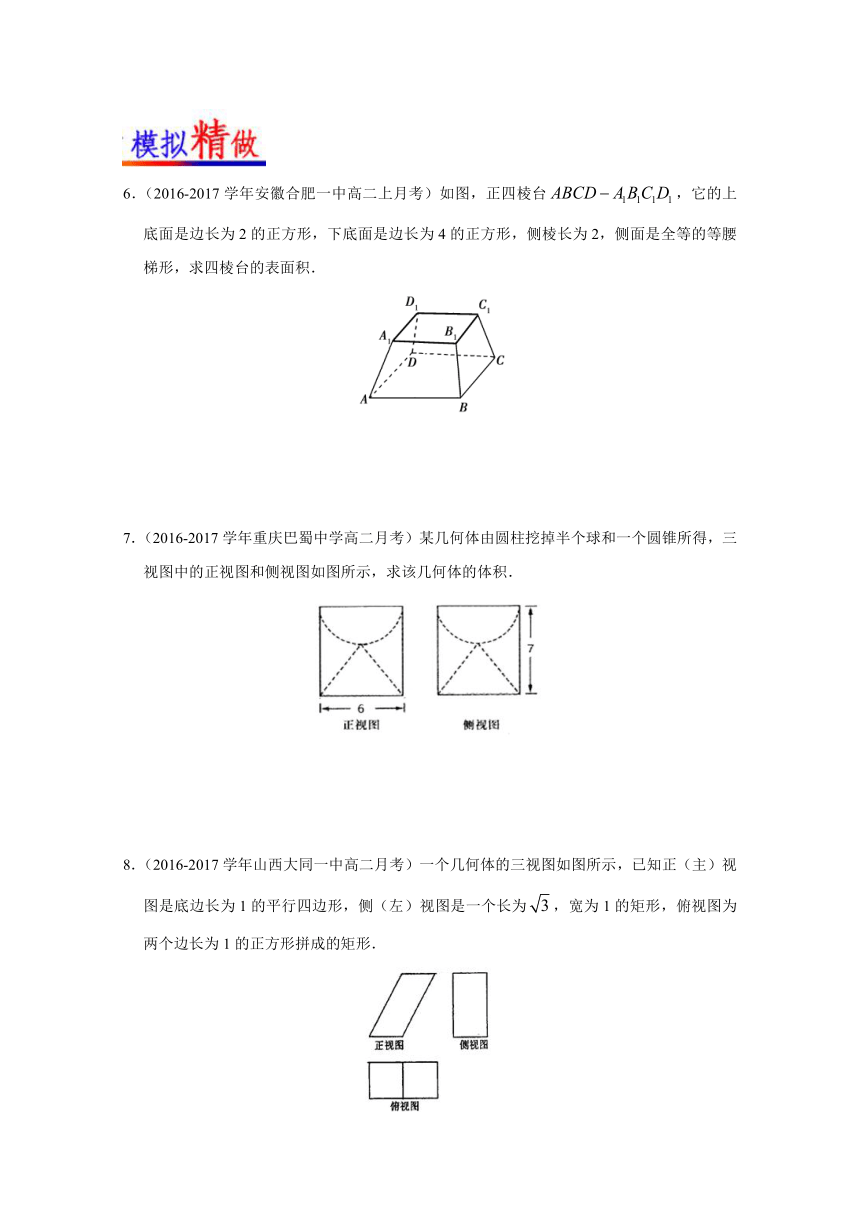
6.(2016-2017学年安徽合肥一中高二上月考)如图,正四棱台,它的上底面是边长为2的正方形,下底面是边长为4的正方形,侧棱长为2,侧面是全等的等腰梯形,求四棱台的表面积.
( http: / / www.21cnjy.com )
7.(2016-2017学年重庆巴蜀中学高
( http: / / www.21cnjy.com )二月考)某几何体由圆柱挖掉半个球和一个圆锥所得,三视图中的正视图和侧视图如图所示,求该几何体的体积.
( http: / / www.21cnjy.com )
8.(2016-2017学年山西大同一中高二月考)一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
( http: / / www.21cnjy.com )
(1)求该几何体的体积;
(2)求该几何体的表面积.
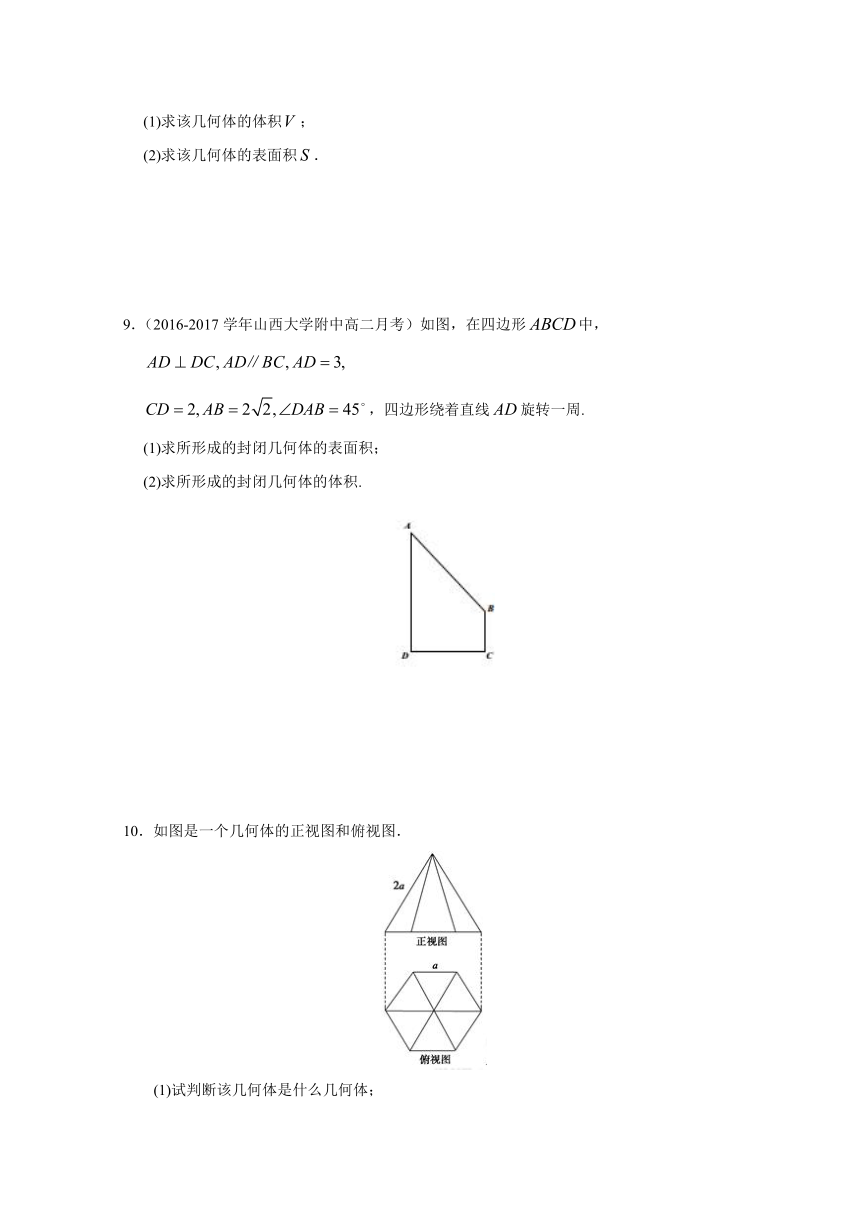
9.(2016-2017学年山西大学附中高二月考)如图,在四边形中,
,四边形绕着直线旋转一周.
(1)求所形成的封闭几何体的表面积;
(2)求所形成的封闭几何体的体积.
( http: / / www.21cnjy.com )
10.如图是一个几何体的正视图和俯视图.
( http: / / www.21cnjy.com )
(1)试判断该几何体是什么几何体;
(2)画出其侧视图,并求该平面图形的面积.
11.(2016·上海文科节选)将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,
长为,长为,其中B1与C在平面AA1O1O的同侧.求圆柱的体积与侧面积.
12.(2016·江苏节选)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥,下部的形状是正四棱柱(如图所示),并要求正四棱柱的高是正四棱锥的高的4倍.若则仓库的容积是多少?
( http: / / www.21cnjy.com )
1.【解析】根据三视图可知,该几何体的直观图如下图所示:
( http: / / www.21cnjy.com )
该正三棱柱底面等边三角形的高为mm,设底面正三角形的边长为mm,正三棱柱的高为mm,则根据侧视图可得,解得,即正三棱柱的底面边长为4
mm,高为2
mm,根据体积公式得(mm3),该三棱柱上、下底面积的和为(mm2),侧面积为(mm2),所以该正三棱柱的表面积为mm2.
2.【解析】由题意知,所求旋转体的表面积由三部分组成:圆台下底面、侧面和半球面.因为,,,故所求几何体的表面积为.
由,,得旋转体的体积为.
3.【解析】(1)设圆柱的底面半径为,则,∴,
则.
(2),∴当时,取得最大值,为,
此时,,所以.
4.【解析】(1)如果正三角形的边长为2,那么倒圆锥形容器的底面半径为1,高为正三角形的高,
于是圆锥形容器的体积.
(2)由题意可知轴截面三角形是正三角形,由球的半径为r,知水深为3r,水面半径为,则容器内水的体积为.设取出铁球后容器中水的深度为h,则水面半径为,
由,得,故将铁球取出后,容器内的水深是.
5.【解析】(1)由已知可得该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥.
(2)作出该几何体的直观图,如图,E、F分别为AB、BC的中点,
则,,,所以体积.
在中,,∴.
在中,,∴,
所以侧面积.
( http: / / www.21cnjy.com )
6.【解析】∵正四棱台的上底面是边长为2的正方形,下底面是边长为4的正方形,
∴上底面、下底面的面积分别是4,16.
∵侧棱长为2,侧面是全等的等腰梯形,∴侧面的高为,
∴侧面的面积为,
∴四棱台的表面积为.
7.【解析】圆柱、圆锥和半个球的半径均为,则圆柱的体积为;半球的体积为;圆锥的体积为.
故所求几何体的体积为.
8.【解析】(1)由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为,所以.
( http: / / www.21cnjy.com )
(2)由三视图可知,该平行六面体中,,,则,侧面为矩形,
故.
9.【解析】(1)旋转后所得的几何体如图所示:
( http: / / www.21cnjy.com )
则表面积.
(2).
10.【解析】(1)由该几何体的正视图及俯视图可知几何体是正六棱锥.
(2)侧视图如图所示:
( http: / / www.21cnjy.com )
其中AB=AC,AD⊥BC,且BC长是俯视图正六边形对边间的距离,即,AD是正六棱锥的高,,所以侧视图的面积为.
11.【解析】由题意可知,圆柱的母线长,底面半径.圆柱的体积,
圆柱的侧面积.
12.【解析】由PO1=2知OO1=4PO1=8.
因为A1B1=AB=6,所以正四棱锥P-A1B1C1D1的体积
正四棱柱ABCD-A1B1C1D1的体积
所以仓库的容积V=V锥+V柱=24+288=312(m3).
1.3空间几何体的表面积与体积
1.一个正三棱柱的三视图如图所示,求这个正三棱柱的体积和表面积.
( http: / / www.21cnjy.com )
2.如下图
(单位:cm),求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积.
( http: / / www.21cnjy.com )
3.如图,已知一个圆锥的底面半径与高均为,且在这个圆锥中有一个高为的圆柱.
( http: / / www.21cnjy.com )
(1)用表示此圆柱的侧面积表达式;
(2)当此圆柱的侧面积最大时,求此圆柱的体积.
4.一个倒圆锥形容器,它的轴截面是正三角形.
(1)如果正三角形的边长为2,求圆锥形容器的体积;
(2)如果在容器内放一个半径为r的铁球(
( http: / / www.21cnjy.com )铁球完全在容器内),并向容器内注水,使水面漫过铁球且恰好与铁球相切(如图所示),则将铁球取出后,容器内的水深是多少
( http: / / www.21cnjy.com )
5.已知某几何体的俯视图是如图所示的矩形.正视图是一个底边长为8、高为4的等腰三角形,侧视图是一个底边长为6、高为4的等腰三角形.
(1)判断该几何体的形状;
(2)求该几何体的体积V与侧面积S.
6.(2016-2017学年安徽合肥一中高二上月考)如图,正四棱台,它的上底面是边长为2的正方形,下底面是边长为4的正方形,侧棱长为2,侧面是全等的等腰梯形,求四棱台的表面积.
( http: / / www.21cnjy.com )
7.(2016-2017学年重庆巴蜀中学高
( http: / / www.21cnjy.com )二月考)某几何体由圆柱挖掉半个球和一个圆锥所得,三视图中的正视图和侧视图如图所示,求该几何体的体积.
( http: / / www.21cnjy.com )
8.(2016-2017学年山西大同一中高二月考)一个几何体的三视图如图所示,已知正(主)视图是底边长为1的平行四边形,侧(左)视图是一个长为,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.
( http: / / www.21cnjy.com )
(1)求该几何体的体积;
(2)求该几何体的表面积.
9.(2016-2017学年山西大学附中高二月考)如图,在四边形中,
,四边形绕着直线旋转一周.
(1)求所形成的封闭几何体的表面积;
(2)求所形成的封闭几何体的体积.
( http: / / www.21cnjy.com )
10.如图是一个几何体的正视图和俯视图.
( http: / / www.21cnjy.com )
(1)试判断该几何体是什么几何体;
(2)画出其侧视图,并求该平面图形的面积.
11.(2016·上海文科节选)将边长为1的正方形AA1O1O(及其内部)绕OO1旋转一周形成圆柱,如图,
长为,长为,其中B1与C在平面AA1O1O的同侧.求圆柱的体积与侧面积.
12.(2016·江苏节选)现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥,下部的形状是正四棱柱(如图所示),并要求正四棱柱的高是正四棱锥的高的4倍.若则仓库的容积是多少?
( http: / / www.21cnjy.com )
1.【解析】根据三视图可知,该几何体的直观图如下图所示:
( http: / / www.21cnjy.com )
该正三棱柱底面等边三角形的高为mm,设底面正三角形的边长为mm,正三棱柱的高为mm,则根据侧视图可得,解得,即正三棱柱的底面边长为4
mm,高为2
mm,根据体积公式得(mm3),该三棱柱上、下底面积的和为(mm2),侧面积为(mm2),所以该正三棱柱的表面积为mm2.
2.【解析】由题意知,所求旋转体的表面积由三部分组成:圆台下底面、侧面和半球面.因为,,,故所求几何体的表面积为.
由,,得旋转体的体积为.
3.【解析】(1)设圆柱的底面半径为,则,∴,
则.
(2),∴当时,取得最大值,为,
此时,,所以.
4.【解析】(1)如果正三角形的边长为2,那么倒圆锥形容器的底面半径为1,高为正三角形的高,
于是圆锥形容器的体积.
(2)由题意可知轴截面三角形是正三角形,由球的半径为r,知水深为3r,水面半径为,则容器内水的体积为.设取出铁球后容器中水的深度为h,则水面半径为,
由,得,故将铁球取出后,容器内的水深是.
5.【解析】(1)由已知可得该几何体是一个底面为矩形,高为4,顶点在底面的射影是矩形中心的四棱锥.
(2)作出该几何体的直观图,如图,E、F分别为AB、BC的中点,
则,,,所以体积.
在中,,∴.
在中,,∴,
所以侧面积.
( http: / / www.21cnjy.com )
6.【解析】∵正四棱台的上底面是边长为2的正方形,下底面是边长为4的正方形,
∴上底面、下底面的面积分别是4,16.
∵侧棱长为2,侧面是全等的等腰梯形,∴侧面的高为,
∴侧面的面积为,
∴四棱台的表面积为.
7.【解析】圆柱、圆锥和半个球的半径均为,则圆柱的体积为;半球的体积为;圆锥的体积为.
故所求几何体的体积为.
8.【解析】(1)由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为,所以.
( http: / / www.21cnjy.com )
(2)由三视图可知,该平行六面体中,,,则,侧面为矩形,
故.
9.【解析】(1)旋转后所得的几何体如图所示:
( http: / / www.21cnjy.com )
则表面积.
(2).
10.【解析】(1)由该几何体的正视图及俯视图可知几何体是正六棱锥.
(2)侧视图如图所示:
( http: / / www.21cnjy.com )
其中AB=AC,AD⊥BC,且BC长是俯视图正六边形对边间的距离,即,AD是正六棱锥的高,,所以侧视图的面积为.
11.【解析】由题意可知,圆柱的母线长,底面半径.圆柱的体积,
圆柱的侧面积.
12.【解析】由PO1=2知OO1=4PO1=8.
因为A1B1=AB=6,所以正四棱锥P-A1B1C1D1的体积
正四棱柱ABCD-A1B1C1D1的体积
所以仓库的容积V=V锥+V柱=24+288=312(m3).
