二次函数复习 第2课时课件
图片预览






文档简介
课件17张PPT。湘教版SHUXUE九年级下x1 ≠ x2xx2x1方程ax2+bx+c=0的解。观察图象,找出抛物线与x轴的交点,再根据交点坐标写出不等式ax2+bx+c>0 或 ax2+bx+c<0的解集。二次函数图像与a,b,c符号的关系:(1)a的符号:确定抛物线的开口方向开口向上a>0开口向下a<0(2)c的符号:确定抛物线与y轴的交点位置.交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0(3)b的符号:由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0(4)b2-4ac的符号:由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0(5)a+b+c的符号:因为x=1时,y=a+b+c,
所以a+b+c的符号由x=1时,对应的y值决定。 当x=1时,y>0, 则a+b+c>0
当x=1时,y<0,则a+b+c<0
当x=1时,y=0,则a+b+c=0(6)a-b+c的符号:因为x=-1时,y=a-b+c,
所以a-b+c的符号由x=-1时,对应的y值决定。当x=-1,y>0,则a-b+c>0
当x=-1,y<0,则a-b+c<0
当x=-1,y=0,则a-b+c=01.在二次函数y=ax2+bx+c中,ac >0, 则它的图像与x轴的关系是( )
A. 没有交点 B. 有两个交点
C. 有一个交点 D. 不能确定B2.已知抛物线y=x2+px+q经过点(5,0),(-5,0),则 p+q=( )
A. 0 B. 25 C. -25 D. 5C3.若二次函数 y=ax2 + b x + c 的图象如下,与x
轴的一个交点为(1,0),则下列各式中不成立的是( )
A. b2-4ac>0 B. abc>0
C. a+b+c=0 D. a-b+c<0 B4.方程x2-3x=0的两根是x1=0,x2=3,抛物线
与x轴交点坐标是( )
A. (0,0) (3,0) B. (0,0) (0,3)
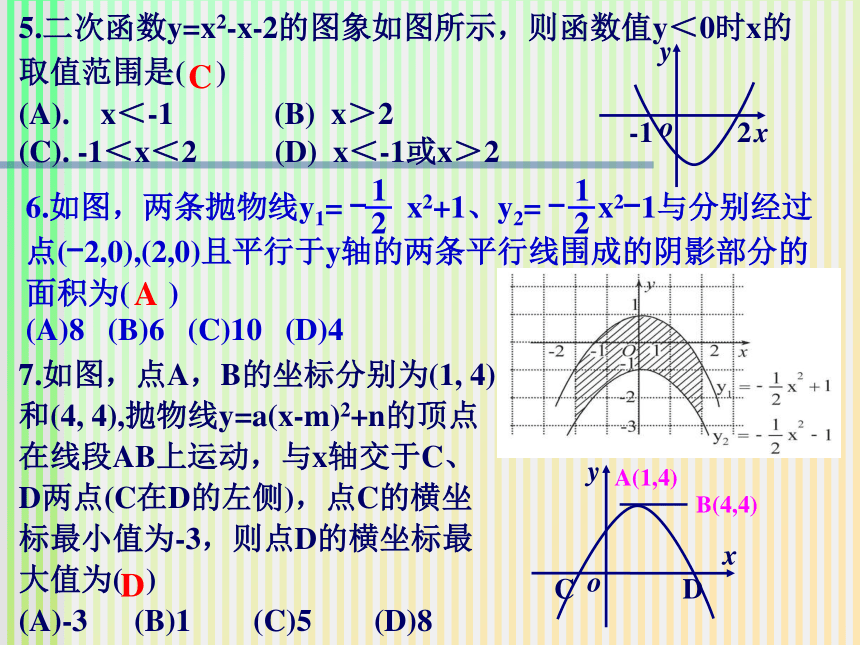
C. (0,0) (-3,0) D. (0,0) (0,-3) A一、选择题C5.二次函数y=x2-x-2的图象如图所示,则函数值y<0时x的取值范围是( )
(A). x<-1 (B) x>2
(C). -1<x<2 (D) x<-1或x>2A7.如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( )
(A)-3 (B)1 (C)5 (D)8D1.已知二次函数y=x2+mx+2的图像与x轴的一个交点是(2,0),则与x轴另一个交点_______,m=_________.(1,0)-3二、填空题2.当m______时,抛物线y=4x2-4x+m与x轴只有一个交点,交点是________.=13. 若二次函数y=kx2+3x-5的图像与x轴有两个交点,则k的取值范围是__________________.4.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=_,此时抛物线 y=x2-2x+m与x轴有__个交点.115.已知实数x,y满足x2+3x+y-3=0,则x+y的最大值为_____.46.已知二次函数y=ax2+bx+c的图像如图,用不等式连结下列各式:a __0,b __0,c ___0,
b2-4ac___0 a+b+c___0, a-b+c___0>>>><<7.若二次函数y=-x2+2x+k的部分图象如图所示,关于x的一元二次方程-x2+2x+k=0的一个解x1=3,另一个解x2=_____.-18.已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2),则此二次函数的解析式 ;设此二次函数的图象与x轴交于A,B两点,O为坐标原点,则线段OA,OB的长度之和是 。9.某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价1元,销量减少10个,设每个涨价x元,销售价可以表示为 ,一个商品所获利润可以表示为 ,销售量可以表示为 ,利润可以为 ,
因此,定价是 元时,最大利润是 元。(50+x)元(50+x-40)元(500-10x) 个(50+x-40)(500-10x)70900010、不论x为何值时,函数y=ax2+bx+c(a≠0)的值永远为正的条件是____ _a>0, b2-4ac<0 y=x2+4x+1 1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。三、解答题:∵二次函数的最大值是2∴抛物线的顶点纵坐标为2顶点在直线y=x+1上当y=2时,x=1∴顶点坐标为( 1 , 2) 设解析式为y=a(x-1)2+2∴a=-2 y=-2(x-1)2+2 y=-2x2+4x2.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式.a=1或a=-1又∵顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5对称轴x=-1,顶点坐标M(-1,-2)图略当x<-1时,y随x的增大而减小;当x=-1时,y最小值=-2 当x< -3或x>1时,y > 0当-3 < x < 1时,y < 04.已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,
其图像构成一个“抛物线系”。下图分别是a=-1,a=0,a=1,
a=2时二次函数的图像。它们的顶点在一直线上,
求这条直线的解析式。由题意知,
二次函数的顶点坐标是(2a,a-1)代入各个a的值,即可得直线解析式5.已知抛物线y=x2-2x-8, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。△=22-4×(-8)=36>0x2-2x-8=0解方程得:x1=4, x2=-2∴AB=4-(-2)=6 而P点坐标是(1,-9)∴S△ABC=27 6、抛物线 y=-2x2+4x+6 顶点为A,与x轴交于B、C两点,与y轴交于D点,求四边形ABCD的面积。y=-2x2+4x+6=-2(x-1)2+8,图像如图A(1,8) B(-1,0) C(3,0) D(0,6)S四边形ABCD=SΔBOD+S梯形OEAD+SΔAEC187.丁丁推铅球的出手高度为1.6m,如图所示,铅球的运行
路线近似为抛物线y=-0.1(x-k)2+2.5①求k的值②求铅球的落点与丁丁的距离.③一个1.5m的小朋友跑到离原点6米的地方(如图),他会受到伤害吗?B(0,1.6)当x=0时,y=1.6k=±3对称轴是在y轴的右侧,即x=k>0,k=3②-0.1(x-3)2+2.5=0得,x1 =8,x2 =-2所以,OB=8
故铅球的落点与丁丁的距离是8米。③当x=6时,y=-0.1(6-3)2+2.5=1.6>1.5所以,这个小朋友不会受到伤害。9、已知二次函数y=ax2-5x+c的图象如图。
(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。
(3)、求它的解析式和顶点坐标;10、某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万。该生产线投产后,从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,若第1年的维修、保养 费用为2万元,到第2年为6万元。
(1)求y的解析式;
(2)投产后,这个企业在第几年就能收回投资?解:(1)由题意,x=1时,y=2;x=2时,y=2+4=6,分别代入y=ax2+bx,得a+b=2,4a+2b=6,
解得:a=1,b=1, ∴y=x2+x.
(2)设f=33x-100-x2-x,则
f=-x2+32x-100=-(x-16)2+156.
由于当1≤x≤16时,f随x的增大而增大,故当x=4时,即第4年可收回投资。11.李明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+500.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2 000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2 000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)(1)由题意,得:w=(x-20)·y=(x-20)·(-10x+500)
=-10x2+700x-10 000
答:当销售单价定为35元时,每月可获得最大利润.(2)由题意,得:-10x2+700x-10 000=2 000
解这个方程得:x1=30,x2=40.
答:李明想要每月获得2 000元的利润,
销售单价应定为30元或40元. (3)方法一:∵a=-10<0,∴抛物线开口向下.
∴当30≤x≤40时,w≥2 000.∵x≤32,∴当30≤x≤32时w≥2000.
设成本为P(元),由题意,得:
P=20×(-10x+500)=-200x+10 000
∵k=-200<0,∴P随x的增大而减小.
∴当x=32时,P最小=3600.
答:每月获得利润不低于2000元,每月成本最少为3600元.方法二:∵a=-10<0,∴抛物线开口向下.
∴当30≤x≤40时,w≥2000.∵x≤32,∴30≤x≤32时,w≥2000.
∵y=-10x+500,k=-10<0,
∴y随x的增大而减小.∴当x=32时,y最小=180.
∵当进价一定时,销售量越小,成本越小,
∴20×180=3 600(元).
答:想要每月获得利润不低于2000元,每月成本最少为3600元.12.用长为12 m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=x m,五边形ABCDE的面积为S m2.问当x取什么值时,S最大?并求出S的最大值.
所以a+b+c的符号由x=1时,对应的y值决定。 当x=1时,y>0, 则a+b+c>0
当x=1时,y<0,则a+b+c<0
当x=1时,y=0,则a+b+c=0(6)a-b+c的符号:因为x=-1时,y=a-b+c,
所以a-b+c的符号由x=-1时,对应的y值决定。当x=-1,y>0,则a-b+c>0
当x=-1,y<0,则a-b+c<0
当x=-1,y=0,则a-b+c=01.在二次函数y=ax2+bx+c中,ac >0, 则它的图像与x轴的关系是( )
A. 没有交点 B. 有两个交点
C. 有一个交点 D. 不能确定B2.已知抛物线y=x2+px+q经过点(5,0),(-5,0),则 p+q=( )
A. 0 B. 25 C. -25 D. 5C3.若二次函数 y=ax2 + b x + c 的图象如下,与x
轴的一个交点为(1,0),则下列各式中不成立的是( )
A. b2-4ac>0 B. abc>0
C. a+b+c=0 D. a-b+c<0 B4.方程x2-3x=0的两根是x1=0,x2=3,抛物线
与x轴交点坐标是( )
A. (0,0) (3,0) B. (0,0) (0,3)
C. (0,0) (-3,0) D. (0,0) (0,-3) A一、选择题C5.二次函数y=x2-x-2的图象如图所示,则函数值y<0时x的取值范围是( )
(A). x<-1 (B) x>2
(C). -1<x<2 (D) x<-1或x>2A7.如图,点A,B的坐标分别为(1, 4)和(4, 4),抛物线y=a(x-m)2+n的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为-3,则点D的横坐标最大值为( )
(A)-3 (B)1 (C)5 (D)8D1.已知二次函数y=x2+mx+2的图像与x轴的一个交点是(2,0),则与x轴另一个交点_______,m=_________.(1,0)-3二、填空题2.当m______时,抛物线y=4x2-4x+m与x轴只有一个交点,交点是________.=13. 若二次函数y=kx2+3x-5的图像与x轴有两个交点,则k的取值范围是__________________.4.如果关于x的一元二次方程 x2-2x+m=0有两个相等的实数根,则m=_,此时抛物线 y=x2-2x+m与x轴有__个交点.115.已知实数x,y满足x2+3x+y-3=0,则x+y的最大值为_____.46.已知二次函数y=ax2+bx+c的图像如图,用不等式连结下列各式:a __0,b __0,c ___0,
b2-4ac___0 a+b+c___0, a-b+c___0>>>><<7.若二次函数y=-x2+2x+k的部分图象如图所示,关于x的一元二次方程-x2+2x+k=0的一个解x1=3,另一个解x2=_____.-18.已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2),则此二次函数的解析式 ;设此二次函数的图象与x轴交于A,B两点,O为坐标原点,则线段OA,OB的长度之和是 。9.某商场将进价40元一个的某种商品按50元一个售出时,能卖出500个,已知这种商品每个涨价1元,销量减少10个,设每个涨价x元,销售价可以表示为 ,一个商品所获利润可以表示为 ,销售量可以表示为 ,利润可以为 ,
因此,定价是 元时,最大利润是 元。(50+x)元(50+x-40)元(500-10x) 个(50+x-40)(500-10x)70900010、不论x为何值时,函数y=ax2+bx+c(a≠0)的值永远为正的条件是____ _a>0, b2-4ac<0 y=x2+4x+1 1、已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6)。求a、b、c。三、解答题:∵二次函数的最大值是2∴抛物线的顶点纵坐标为2顶点在直线y=x+1上当y=2时,x=1∴顶点坐标为( 1 , 2) 设解析式为y=a(x-1)2+2∴a=-2 y=-2(x-1)2+2 y=-2x2+4x2.已知抛物线y=ax2+bx+c与抛物线y=-x2-3x+7的形状相同,顶点在直线x=1上,且顶点到x轴的距离为5,请写出满足此条件的抛物线的解析式.a=1或a=-1又∵顶点在直线x=1上,且顶点到x轴的距离为5,
? 顶点为(1,5)或(1,-5)所以其解析式为:
(1) y=(x-1)2+5 (2) y=(x-1)2-5
(3) y=-(x-1)2+5 (4) y=-(x-1)2-5对称轴x=-1,顶点坐标M(-1,-2)图略当x<-1时,y随x的增大而减小;当x=-1时,y最小值=-2 当x< -3或x>1时,y > 0当-3 < x < 1时,y < 04.已知二次函数y=(x-2a)2+(a-1)(a为常数),当a取不同的值时,
其图像构成一个“抛物线系”。下图分别是a=-1,a=0,a=1,
a=2时二次函数的图像。它们的顶点在一直线上,
求这条直线的解析式。由题意知,
二次函数的顶点坐标是(2a,a-1)代入各个a的值,即可得直线解析式5.已知抛物线y=x2-2x-8, (1)求证:该抛物线与x轴一定有两个交点; (2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积。△=22-4×(-8)=36>0x2-2x-8=0解方程得:x1=4, x2=-2∴AB=4-(-2)=6 而P点坐标是(1,-9)∴S△ABC=27 6、抛物线 y=-2x2+4x+6 顶点为A,与x轴交于B、C两点,与y轴交于D点,求四边形ABCD的面积。y=-2x2+4x+6=-2(x-1)2+8,图像如图A(1,8) B(-1,0) C(3,0) D(0,6)S四边形ABCD=SΔBOD+S梯形OEAD+SΔAEC187.丁丁推铅球的出手高度为1.6m,如图所示,铅球的运行
路线近似为抛物线y=-0.1(x-k)2+2.5①求k的值②求铅球的落点与丁丁的距离.③一个1.5m的小朋友跑到离原点6米的地方(如图),他会受到伤害吗?B(0,1.6)当x=0时,y=1.6k=±3对称轴是在y轴的右侧,即x=k>0,k=3②-0.1(x-3)2+2.5=0得,x1 =8,x2 =-2所以,OB=8
故铅球的落点与丁丁的距离是8米。③当x=6时,y=-0.1(6-3)2+2.5=1.6>1.5所以,这个小朋友不会受到伤害。9、已知二次函数y=ax2-5x+c的图象如图。
(1)、当x为何值时,y随x的增大而增大;
(2)、当x为何值时,y<0。
(3)、求它的解析式和顶点坐标;10、某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万。该生产线投产后,从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,若第1年的维修、保养 费用为2万元,到第2年为6万元。
(1)求y的解析式;
(2)投产后,这个企业在第几年就能收回投资?解:(1)由题意,x=1时,y=2;x=2时,y=2+4=6,分别代入y=ax2+bx,得a+b=2,4a+2b=6,
解得:a=1,b=1, ∴y=x2+x.
(2)设f=33x-100-x2-x,则
f=-x2+32x-100=-(x-16)2+156.
由于当1≤x≤16时,f随x的增大而增大,故当x=4时,即第4年可收回投资。11.李明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=-10x+500.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2 000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2 000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)(1)由题意,得:w=(x-20)·y=(x-20)·(-10x+500)
=-10x2+700x-10 000
答:当销售单价定为35元时,每月可获得最大利润.(2)由题意,得:-10x2+700x-10 000=2 000
解这个方程得:x1=30,x2=40.
答:李明想要每月获得2 000元的利润,
销售单价应定为30元或40元. (3)方法一:∵a=-10<0,∴抛物线开口向下.
∴当30≤x≤40时,w≥2 000.∵x≤32,∴当30≤x≤32时w≥2000.
设成本为P(元),由题意,得:
P=20×(-10x+500)=-200x+10 000
∵k=-200<0,∴P随x的增大而减小.
∴当x=32时,P最小=3600.
答:每月获得利润不低于2000元,每月成本最少为3600元.方法二:∵a=-10<0,∴抛物线开口向下.
∴当30≤x≤40时,w≥2000.∵x≤32,∴30≤x≤32时,w≥2000.
∵y=-10x+500,k=-10<0,
∴y随x的增大而减小.∴当x=32时,y最小=180.
∵当进价一定时,销售量越小,成本越小,
∴20×180=3 600(元).
答:想要每月获得利润不低于2000元,每月成本最少为3600元.12.用长为12 m的篱笆,一边利用足够长的墙围出一块苗圃.如图,围出的苗圃是五边形ABCDE,AE⊥AB,BC⊥AB,∠C=∠D=∠E.设CD=DE=x m,五边形ABCDE的面积为S m2.问当x取什么值时,S最大?并求出S的最大值.
