九年级下2.4过不共线三点作圆课件(共10张)
文档属性
| 名称 | 九年级下2.4过不共线三点作圆课件(共10张) |

|
|
| 格式 | zip | ||
| 文件大小 | 162.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览




文档简介
课件10张PPT。过不共线三点作圆问题情境小明不小心将妈妈的圆形化妆镜打碎
了(如图),他想“破镜重圆”,
应该拿哪一块去维修店修复?过一点可作几条直线?过两点可以作几条直线?过三点呢?1、若三点共线,则过这三点只能作一条直线.2、若三点不共线,则过这三点不能作直线,但过其中任意两点一共可作三条直线.直线公理::两点确定一条直线·类比探究对于一个圆来说,过几个点能作一个圆,
并且只能作一个圆?1、过一点能作几个圆?·····经过一个已知点能作无数个圆2、过两点能作几个圆?····经过两个已知点能作无数个圆以平面上除A点外的任意一点为圆心,任意长为半径作圆。以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.3、过三点能作几个圆?(1)三点共线:(不能作圆)因为DE∥FG,所以没有交点,
即没有过这三点的圆心(2)三点不共线已知:不在同一直线上的
三点A、B、C
求作:⊙O,使它经过A、B、C如何确定圆心、半径?·∵直线DE和FG只有一个交点O,
并且点O到A,B,C三个点的距离相等,∴经过点A,B,C三点可以作一个圆,
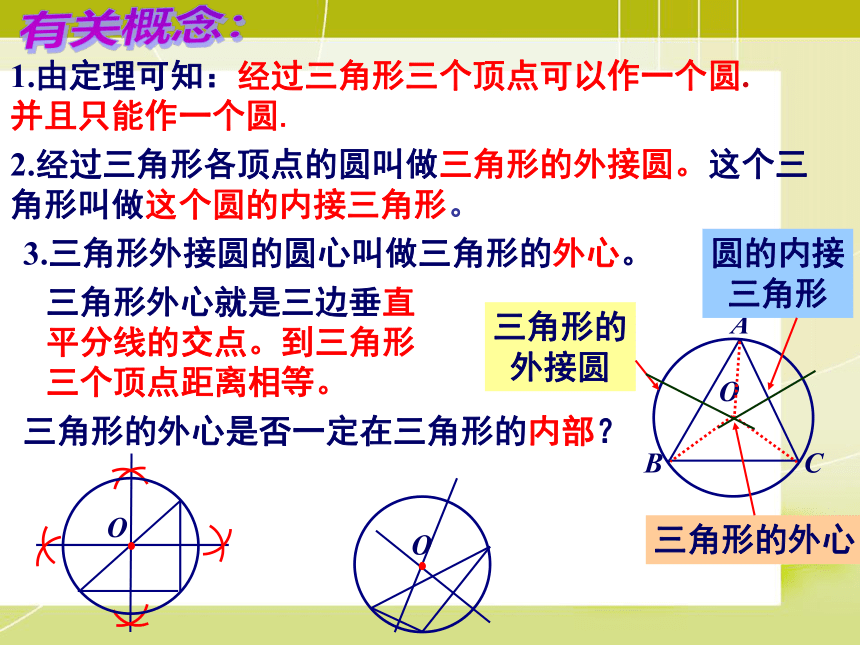
并且只能作一个圆.∴OA=OB=OC.证明作图的合理性:定理:不在同一直线上的三点确定一个圆DEFG有关概念:1.由定理可知:经过三角形三个顶点可以作一个圆.
并且只能作一个圆.2.经过三角形各顶点的圆叫做三角形的外接圆。这个三角形叫做这个圆的内接三角形。3.三角形外接圆的圆心叫做三角形的外心。三角形外心就是三边垂直
平分线的交点。到三角形
三个顶点距离相等。三角形的外心是否一定在三角形的内部?1、如何解决“破镜重圆”的问题:·2、为美化校园,学校要把一块三角形空地扩建成一个圆形喷水池,在三角形三个顶点处各有一棵名贵花树(A、B、C),若不动花树,还要建一个最大的圆形喷水池,请设计你的实施方案。做三角形的外接圆想一想:过不共线的四点能作一个圆吗?1.已知点A、B分别在∠MON的边OM、ON上,
则经过点A、O、B能作圆的个数是 .1个2.下列说法正确的是( )
A.经过三点一定可以作圆。
B.任意一个圆一定有内接三角形,且只有一个内接三角形。
C.任意一个三角形一定有一个外接圆,且只有一个外接圆。
D.三角形外心到三角形三边的距离都相等。C3.下列条件,可以确定一个圆的是( )
A.已知圆心。 B.已知半径长。
C.已知直径长。D.已知不在同一直线上的三点。DA5.如图,OA=OB=OC,且∠ACB=30°,
则∠AOB是( )
A.40° B.50° C.60° D.70° 6.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是( )
A.(2,3) B.(3,2) C.(1,3) D.(3,1)7. 求边长为a的等边三角形的外接圆的半径.CD8. 如果直角三角形的两条直角边分别是6,8,求出这个直角三角形的外接圆的面积吗?9.在△ABC中,AB=AC=13,BC=10,
试求这个三角形的外接圆的半径.10.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=2,求⊙O的直径及AC边长。直角三角形的外心是斜边的中点。
外接圆的半径等于斜边一半。作AD⊥BC,垂足为D,连结OBAD=12设半径为R,有:R2=52+(12-R)2∵∠B=60°∴∠AOC=120°,∴∠AOP=60°,∴OA=4,过两点可以作无数个圆.圆心在以已
知两点为端点的线段的垂直平分线上.实际问题直线
公理过一点可以作无数个圆过在同一直线上的三点不能作圆外心、三角形外接圆、
圆的内接三角形实际问题作圆课堂小结我学会了什么 ?
了(如图),他想“破镜重圆”,
应该拿哪一块去维修店修复?过一点可作几条直线?过两点可以作几条直线?过三点呢?1、若三点共线,则过这三点只能作一条直线.2、若三点不共线,则过这三点不能作直线,但过其中任意两点一共可作三条直线.直线公理::两点确定一条直线·类比探究对于一个圆来说,过几个点能作一个圆,
并且只能作一个圆?1、过一点能作几个圆?·····经过一个已知点能作无数个圆2、过两点能作几个圆?····经过两个已知点能作无数个圆以平面上除A点外的任意一点为圆心,任意长为半径作圆。以线段AB的垂直平分线上的任意一点为圆心,这点到A或B的距离为半径作圆.3、过三点能作几个圆?(1)三点共线:(不能作圆)因为DE∥FG,所以没有交点,
即没有过这三点的圆心(2)三点不共线已知:不在同一直线上的
三点A、B、C
求作:⊙O,使它经过A、B、C如何确定圆心、半径?·∵直线DE和FG只有一个交点O,
并且点O到A,B,C三个点的距离相等,∴经过点A,B,C三点可以作一个圆,
并且只能作一个圆.∴OA=OB=OC.证明作图的合理性:定理:不在同一直线上的三点确定一个圆DEFG有关概念:1.由定理可知:经过三角形三个顶点可以作一个圆.
并且只能作一个圆.2.经过三角形各顶点的圆叫做三角形的外接圆。这个三角形叫做这个圆的内接三角形。3.三角形外接圆的圆心叫做三角形的外心。三角形外心就是三边垂直
平分线的交点。到三角形
三个顶点距离相等。三角形的外心是否一定在三角形的内部?1、如何解决“破镜重圆”的问题:·2、为美化校园,学校要把一块三角形空地扩建成一个圆形喷水池,在三角形三个顶点处各有一棵名贵花树(A、B、C),若不动花树,还要建一个最大的圆形喷水池,请设计你的实施方案。做三角形的外接圆想一想:过不共线的四点能作一个圆吗?1.已知点A、B分别在∠MON的边OM、ON上,
则经过点A、O、B能作圆的个数是 .1个2.下列说法正确的是( )
A.经过三点一定可以作圆。
B.任意一个圆一定有内接三角形,且只有一个内接三角形。
C.任意一个三角形一定有一个外接圆,且只有一个外接圆。
D.三角形外心到三角形三边的距离都相等。C3.下列条件,可以确定一个圆的是( )
A.已知圆心。 B.已知半径长。
C.已知直径长。D.已知不在同一直线上的三点。DA5.如图,OA=OB=OC,且∠ACB=30°,
则∠AOB是( )
A.40° B.50° C.60° D.70° 6.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是( )
A.(2,3) B.(3,2) C.(1,3) D.(3,1)7. 求边长为a的等边三角形的外接圆的半径.CD8. 如果直角三角形的两条直角边分别是6,8,求出这个直角三角形的外接圆的面积吗?9.在△ABC中,AB=AC=13,BC=10,
试求这个三角形的外接圆的半径.10.如图,⊙O是△ABC的外接圆,∠B=60°,OP⊥AC于点P,OP=2,求⊙O的直径及AC边长。直角三角形的外心是斜边的中点。
外接圆的半径等于斜边一半。作AD⊥BC,垂足为D,连结OBAD=12设半径为R,有:R2=52+(12-R)2∵∠B=60°∴∠AOC=120°,∴∠AOP=60°,∴OA=4,过两点可以作无数个圆.圆心在以已
知两点为端点的线段的垂直平分线上.实际问题直线
公理过一点可以作无数个圆过在同一直线上的三点不能作圆外心、三角形外接圆、
圆的内接三角形实际问题作圆课堂小结我学会了什么 ?
