人教A版必修二第二章2.3.1 直线与平面垂直的判定 课件
文档属性
| 名称 | 人教A版必修二第二章2.3.1 直线与平面垂直的判定 课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览






文档简介
课件91张PPT。复习回顾:空间直线和平面有几种位置关系?大桥的桥柱与水面垂直生活中有很多直线与平面垂直的实例实例引入
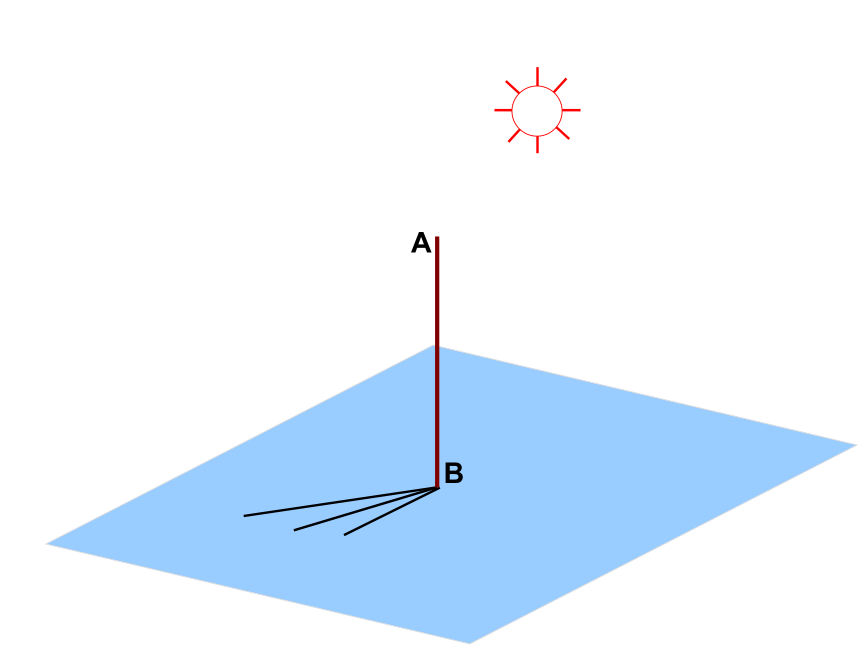
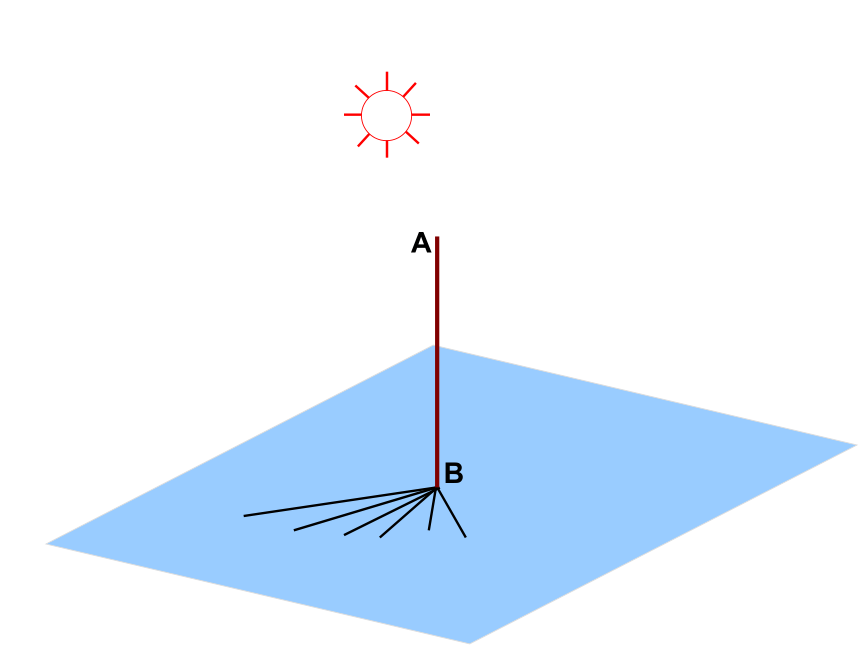
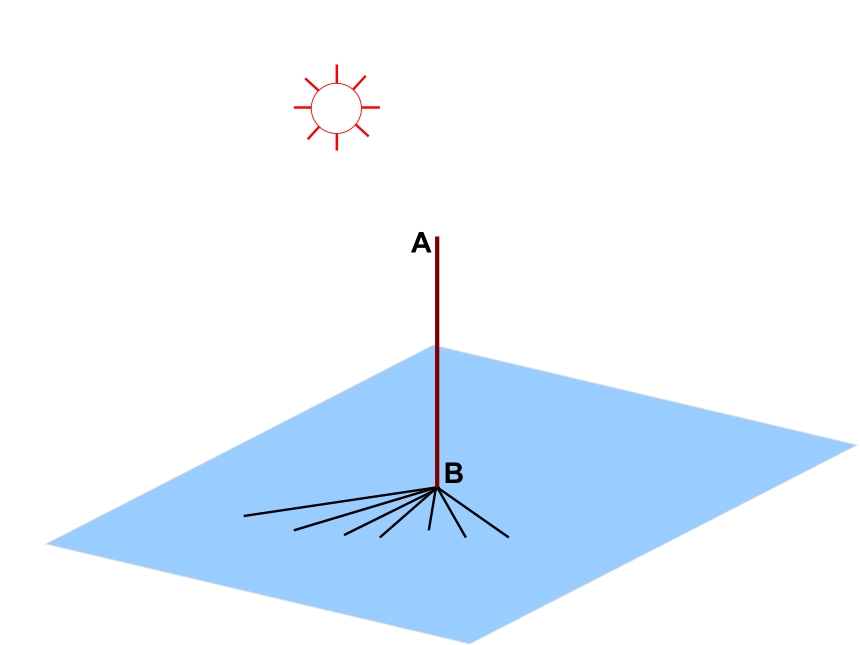
大漠孤烟直 α内过点B的直线AB所在直线内不过点B的直线ααAB所在直线内任意一条直线αAB所在直线⊥⊥⊥一、直线和平面垂直的定义如果一条直线和一个平面相交,并且和这个平面内的任意一条直线都垂直,我们就说这条直线和这个平面垂直.其中直线叫做平面的垂线,平面叫做直线的垂面.交点叫做垂足.平面的垂线直线的垂面垂足直线和平面垂直的画法: 通常把直线画成和表示平面的平行四边形的一边垂直。深入理解“线面垂直定义”判断下列语句是否正确:(若不正确请举反例)
1.如果一条直线与一个平面垂直,那么它与平面内所有的直线都垂直. ( )
2.如果一条直线与平面内无数条直线都垂直,那么它与平面垂直. ( ) 利用定义,我们得到了判定线面垂直的最基本方法,同时也得到了线面垂直的最基本的性质.探索新知: 但是,直接考察直线与平面内所有直线都垂直是不可能的,这就有必要去寻找比定义法更简捷、更可行的直线与平面垂直的方法!探索新知:做一做
想一想1.折痕AD与桌面垂直吗?
2.如何翻折才能使折痕AD与桌面所在的平面垂直? 请同学们拿出一块三角形纸片,我们一起做一个试验:过三角形的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触)2.如何翻折才能使折痕AD与桌面所在的平面垂直?探索新知:探索新知: 由刚才分析可以知道,直线与平面垂直的判定需要哪几个条件?你能根据刚才的分析归纳出直线与平面垂
直判定定理吗 (1) 平面有两条直线
(2) 这两条直线要相交
(3) 平面外的直线要与这两条直线都垂直二、 直线与平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。一相交两垂直判断下列命题是否正确?
(1)过一点有且只有一条直线和一个平面垂直( )
(2)过一点有且只有一个平面和一条直线垂直( )√√例1.在下图的长方体中,请列举与平面ABCD垂直的直线。并说明这些直线有怎样的位置关系?例2、在正方体AC1中,求证:(2)D1B⊥平面ACB1(1)AC⊥平面D1DB例2、在正方体AC1中,求证:(2)D1B⊥平面ACB1由异成直线所成的角知D1B⊥平面ACB1例3、三棱锥V-ABC中,VA=VC,AB=BC,K是AC的中点。
(1)求证:AC ⊥平面VKB (2)求证:VB ⊥AC(1)连接VK,KB,由VA=VC,K为AC中点,由三线合一可知VK ⊥AC,
同理可得KB ⊥AC,且VK∩KB=K
所以AC ⊥平面VKB (判定定理)变式:1、在例3中若E、F分别为AB、BC 的中点,试判断EF与平面VKB的位置关系. 例3、三棱锥V-ABC中,VA=VC,AB=BC,K是AC的中点。
(1)求证:AC ⊥平面VKB (2)求证:VB ⊥AC直线与平面垂直的性质 过一点向平面引垂线,垂足叫做这点在这个平面上的射影; 这点与垂足间的线段叫做这点到这个平面的垂线段。一.斜线在平面内的射影1.垂线、斜线、射影(1)垂线线段PQ(2)斜线 一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线. 斜线和平面的交点叫做斜足。 从平面外一点向平面引斜线,这点与斜足间的线段叫做这点到这个平面的斜线段PRACB 过斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面上的射影. 垂足与斜足间的线段叫做这点到平面的斜线段在这个平面上的射影.(3)射影直线BCACBFE说明:②斜线上任意一点在平面上的射影,一定在斜线的射影上。思考:斜线上的一个点在平面上的射影会在哪呢?思考:
①从平面外一点向这个平面引的垂线段和斜线段,它们的射影和线段本身之间有什么关系?
②从平面外一点向这个平面所引的垂线段和斜线段AB、AC、AD、AE…中,那一条最短?ACBDE 垂线段比任何
一条斜线段都短 如果两条直线同时垂直于一个平面,那么
这两条直线平行。3.直线与平面垂直的性质定理 例2、如图,已知AC、AB分别是平面α的垂线和斜 线,C、B分别是垂足和斜足,a ,a⊥BC。
求证:a⊥AB
线面垂直线线垂直三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它就和这条斜线垂直.三垂线定理的逆定理:如果平面内的一条直线与这个平面的一条斜线垂直,那么这条直线就和这条斜线在这个平面内的射影垂直.求证: a⊥BC
外中垂巩固练习:已知三棱锥P-ABC的三条侧棱PA=PB=PC
试判断点P在底面ABC的射影的位置?PABCOOA=OB=OCO为三角形ABC的外心已知三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,试判断点P在底面ABC的射影的位置?PABCO为三角形ABC的垂心DO已知三棱锥P-ABC的顶点P到底面三角形ABC的三条边的距离相等,试判断点P在底面ABC的射影的位置?PABCO为三角形ABC的内心OEF典型:四面体P-ABC的顶点P在平面上的射影为O(1)P到三顶点距离相等(3)P到三边AB、BC、AC距离相等(2)侧棱两两垂直外垂内若三棱锥有两组对边互相垂直,则另一组对边必然垂直O是垂心练习3.如果两直线垂直于同一个平面,那么这
两条直线平行.练习2.过一点只有一个平面和一条直线垂直.练习1.过一点只有一条直线和一个平面垂直.结论1.结论2.结论3. 常用结论发散结论1:过一点有且只有一个平面和已知直线垂直。结论2:如果两条平行直线中的一条垂直于一个平面,那么另一条直线也垂直于这个平面。结论3:如果两条直线同垂直于一个平面,那么这两条直线平行。直线和平面垂直的判定 例 求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面。 √√√小试牛刀线面垂直的性质定理:符号语言:图形语言:垂直于同一平面的两直线互相平行.例2.如图,已知a∥b、a⊥α.
求证:b⊥α.(线面垂直 线线垂直)(线线垂直 线面垂直)例2、如图,已知a∥b,a⊥α。
求证:b⊥α。例题示范,巩固新知分析:在平面内作两条相交直线,由直线与平面垂直的定义可知,直线a与这两条相交直线是垂直的,又由b平行a,可证b与这两条相交直线也垂直,从而可证直线与平面垂直。ab阅读P66页的证明过程.√×1、判断下列命题的正误。(2)垂直于同一直线的两条直线互相平行( )(3)平行于同一平面的两条直线互相平行( )(4)垂直于同一平面的两条直线互相平行( )×(1)平行于同一直线的两条直线互相平行( )√五、过程设计(三) 线面垂直性质定理的应用小牛试刀(1)若PA=PB=PC,则O是△ABC的 .PABC?O外心例4.关于三角形的四心问题 设O为三棱锥P—ABC的顶点P在底面上的射影.综合练习:(2)若PA=PB=PC,∠C=900,则O是AB的_____点.中PABC?O例4.关于三角形的四心问题综合练习:垂心EFPABC?O (3)若三条側棱两两互相垂直,则O是△ABC的 .例4.关于三角形的四心问题综合练习:EFPABC?O (5)若三条側棱与底面成相等的角,则O是△ABC的_____. 外心例4.关于三角形的四心问题综合练习:例1、已知直角△ABC所在平面外有一点P,且PA=PB=PC,D是斜边AB的中点,
求证:PD⊥平面ABC. 证明:PA=PB,D为AB中点
∴ PD⊥AB,连接CD,
∵D为Rt△ABC斜边的中点
∴ CD=AD, 又PA=PC,PD=PD
∴ △PAD≌△PCD 而PD⊥AB
∴ PD⊥CD, CD∩AB = D
∴PD⊥平面ABC例2、如图 平面α、β相交于PQ,
线段OA、OB分别垂直平面α、β,
求证:PQ⊥AB证明:∵OA⊥α PQ?α
∴ OA⊥PQ
OB⊥β, PQ?β
∴ OB⊥PQ
又OA∩OB=0
∴PQ⊥平面OAB
而AB?平面OAB
∴ PQ⊥ABSABCHSABCH1.如图,已知点M是菱形ABCD所在平面外一点,且MA=MC
求证:AC⊥平面BDMMABCDOABCD证明: 2. 在空间四边形ABCD中,AB=AD,CB=CD,
求证:对角线AC BD。 3.如图,圆O所在一平面为 ,AB是圆O 的直径,C 在圆周上, 且PA AC, PA AB,
求证:(1)PA BC
(2)BC 平面PAC典例 平面内有一个三角形ABC,平面外有一点P,自P向平面作斜线PA,PB,PC,且PA=PB=PC,若点O是△ABC的外心,求证:PO⊥平面ABC.【解】 如图所示,分别取AB,BC的中点D,E,连接PD,PE,OD,OE.
因为PA=PB=PC,
所以PD⊥AB,PE⊥BC,
因为O是△ABC的外心,
所以OD⊥AB,OE⊥BC,
又因为PD∩DO=D,OE∩PE=E,
所以AB⊥平面PDO,BC⊥平面PEO,
于是有AB⊥PO,BC⊥PO,AB∩BC=B,
从而推得PO⊥平面ABC.中外垂重心:三条中线的交点
垂心:三条高的交点
外心:三条垂直平分线的交点(到△三个顶点的距离相等)
内心:三角平分线的交点
中心:正△的重心、垂心、内心、外心重合的点巩固练习VABC直线与平面垂直的判定与性质 解题分析:解题小结:2018-10-23例1:如图,已知AC、AB分别是平面α的垂线
和斜线,C、B分别是垂足和斜足,a α,
a⊥BC.求证:a⊥AB. ACBaα射影垂直,斜线垂直2018-10-23例2:如图,∠BAC在平面α内,P为平面α外一
点,∠PAB=∠PAC.求证:点P在平面α上
的射影在∠BAC的平分线上. ACBPαOEF巩固练习1.平行四边形ABCD所在平面a外有一点P,且PA=PB=PC=PD,求证:点P与平行四边形对角线交点O的连线PO垂直于AB、AD.2018-10-23例2:如图,在棱长为1的正方体中.
(1)求B1D 与平面ABCD所成的角的正切;O(2)求A1C1 与平面ABC1D1所成的角;(3)求BB1 与平面A1BC1所成的角的正切.MH2018-10-23例5:⊿ABC的定点在平面α内,点A、C在平面
α的同侧,AB、BC与α所成角分别是300和
450.若AB=3,BC=4√2,AC=5,求AC
与平面α所成的角. AαBC2018-10-23例6:如图,P是正方形ABCD所在平面外一点,
PA⊥平面ABCD,AE ⊥ PD,PA=3AB.求
直线AC与平面ABE所成角的正弦值. PABCDE 【5】如图, AB为平面α的一条斜线, B为斜足,AO⊥平面α, 垂足为O, 直线BC在平面α内,已知∠ABC=60°,∠OBC=45°, 则斜线AB和平面α所成的角是_______.ACODBα45°设OB=2,补充练习引课我们知道,当直线和平面垂直时,该直线叫做平面的垂线。如果直线和平面不垂直,是不是也该给它取个名字呢?此时又该如何刻画直线和平面的这种关系呢?直线与平面所成的角1.平面的斜线如图,若一条直线PA和一个平面α相交,但不垂直,那么这条直线就叫做这个平面的斜线,斜线和平面的交点A叫做斜足。PA斜足斜线例1、如图,正方体ABCD-A1B1C1D1中,求
(1)直线A1B和平面 BCC1B1所成的角。
(2)直线A1B和平面A1B1CD所成的角。O例题示范,巩固新知分析:找出直线A1B在平面BCC1B1和平面A1B1CD内的射影,就可以求出A1B和平面BCC1B1和平面A1B1CD所成的角。阅读教科书P67上的解答过程HC与平面ABCD 所成的角是?BG和EA与平面ABCD所成的角 分别是?∠GBC与∠EAB∠HCDEC和EG与平面ABCD所成的角分别是?∠ACE练习:正方体ABCD-EFGH中
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影A1D1C1B1ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB0o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB90o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB45o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB30o巩固练习线线垂直相交垂直(共面垂直)异面垂直
大漠孤烟直 α内过点B的直线AB所在直线内不过点B的直线ααAB所在直线内任意一条直线αAB所在直线⊥⊥⊥一、直线和平面垂直的定义如果一条直线和一个平面相交,并且和这个平面内的任意一条直线都垂直,我们就说这条直线和这个平面垂直.其中直线叫做平面的垂线,平面叫做直线的垂面.交点叫做垂足.平面的垂线直线的垂面垂足直线和平面垂直的画法: 通常把直线画成和表示平面的平行四边形的一边垂直。深入理解“线面垂直定义”判断下列语句是否正确:(若不正确请举反例)
1.如果一条直线与一个平面垂直,那么它与平面内所有的直线都垂直. ( )
2.如果一条直线与平面内无数条直线都垂直,那么它与平面垂直. ( ) 利用定义,我们得到了判定线面垂直的最基本方法,同时也得到了线面垂直的最基本的性质.探索新知: 但是,直接考察直线与平面内所有直线都垂直是不可能的,这就有必要去寻找比定义法更简捷、更可行的直线与平面垂直的方法!探索新知:做一做
想一想1.折痕AD与桌面垂直吗?
2.如何翻折才能使折痕AD与桌面所在的平面垂直? 请同学们拿出一块三角形纸片,我们一起做一个试验:过三角形的顶点A翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD、DC与桌面接触)2.如何翻折才能使折痕AD与桌面所在的平面垂直?探索新知:探索新知: 由刚才分析可以知道,直线与平面垂直的判定需要哪几个条件?你能根据刚才的分析归纳出直线与平面垂
直判定定理吗 (1) 平面有两条直线
(2) 这两条直线要相交
(3) 平面外的直线要与这两条直线都垂直二、 直线与平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。一相交两垂直判断下列命题是否正确?
(1)过一点有且只有一条直线和一个平面垂直( )
(2)过一点有且只有一个平面和一条直线垂直( )√√例1.在下图的长方体中,请列举与平面ABCD垂直的直线。并说明这些直线有怎样的位置关系?例2、在正方体AC1中,求证:(2)D1B⊥平面ACB1(1)AC⊥平面D1DB例2、在正方体AC1中,求证:(2)D1B⊥平面ACB1由异成直线所成的角知D1B⊥平面ACB1例3、三棱锥V-ABC中,VA=VC,AB=BC,K是AC的中点。
(1)求证:AC ⊥平面VKB (2)求证:VB ⊥AC(1)连接VK,KB,由VA=VC,K为AC中点,由三线合一可知VK ⊥AC,
同理可得KB ⊥AC,且VK∩KB=K
所以AC ⊥平面VKB (判定定理)变式:1、在例3中若E、F分别为AB、BC 的中点,试判断EF与平面VKB的位置关系. 例3、三棱锥V-ABC中,VA=VC,AB=BC,K是AC的中点。
(1)求证:AC ⊥平面VKB (2)求证:VB ⊥AC直线与平面垂直的性质 过一点向平面引垂线,垂足叫做这点在这个平面上的射影; 这点与垂足间的线段叫做这点到这个平面的垂线段。一.斜线在平面内的射影1.垂线、斜线、射影(1)垂线线段PQ(2)斜线 一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线. 斜线和平面的交点叫做斜足。 从平面外一点向平面引斜线,这点与斜足间的线段叫做这点到这个平面的斜线段PRACB 过斜线上斜足以外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面上的射影. 垂足与斜足间的线段叫做这点到平面的斜线段在这个平面上的射影.(3)射影直线BCACBFE说明:②斜线上任意一点在平面上的射影,一定在斜线的射影上。思考:斜线上的一个点在平面上的射影会在哪呢?思考:
①从平面外一点向这个平面引的垂线段和斜线段,它们的射影和线段本身之间有什么关系?
②从平面外一点向这个平面所引的垂线段和斜线段AB、AC、AD、AE…中,那一条最短?ACBDE 垂线段比任何
一条斜线段都短 如果两条直线同时垂直于一个平面,那么
这两条直线平行。3.直线与平面垂直的性质定理 例2、如图,已知AC、AB分别是平面α的垂线和斜 线,C、B分别是垂足和斜足,a ,a⊥BC。
求证:a⊥AB
线面垂直线线垂直三垂线定理:在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它就和这条斜线垂直.三垂线定理的逆定理:如果平面内的一条直线与这个平面的一条斜线垂直,那么这条直线就和这条斜线在这个平面内的射影垂直.求证: a⊥BC
外中垂巩固练习:已知三棱锥P-ABC的三条侧棱PA=PB=PC
试判断点P在底面ABC的射影的位置?PABCOOA=OB=OCO为三角形ABC的外心已知三棱锥P-ABC的三条侧棱PA,PB,PC两两垂直,试判断点P在底面ABC的射影的位置?PABCO为三角形ABC的垂心DO已知三棱锥P-ABC的顶点P到底面三角形ABC的三条边的距离相等,试判断点P在底面ABC的射影的位置?PABCO为三角形ABC的内心OEF典型:四面体P-ABC的顶点P在平面上的射影为O(1)P到三顶点距离相等(3)P到三边AB、BC、AC距离相等(2)侧棱两两垂直外垂内若三棱锥有两组对边互相垂直,则另一组对边必然垂直O是垂心练习3.如果两直线垂直于同一个平面,那么这
两条直线平行.练习2.过一点只有一个平面和一条直线垂直.练习1.过一点只有一条直线和一个平面垂直.结论1.结论2.结论3. 常用结论发散结论1:过一点有且只有一个平面和已知直线垂直。结论2:如果两条平行直线中的一条垂直于一个平面,那么另一条直线也垂直于这个平面。结论3:如果两条直线同垂直于一个平面,那么这两条直线平行。直线和平面垂直的判定 例 求证:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面。 √√√小试牛刀线面垂直的性质定理:符号语言:图形语言:垂直于同一平面的两直线互相平行.例2.如图,已知a∥b、a⊥α.
求证:b⊥α.(线面垂直 线线垂直)(线线垂直 线面垂直)例2、如图,已知a∥b,a⊥α。
求证:b⊥α。例题示范,巩固新知分析:在平面内作两条相交直线,由直线与平面垂直的定义可知,直线a与这两条相交直线是垂直的,又由b平行a,可证b与这两条相交直线也垂直,从而可证直线与平面垂直。ab阅读P66页的证明过程.√×1、判断下列命题的正误。(2)垂直于同一直线的两条直线互相平行( )(3)平行于同一平面的两条直线互相平行( )(4)垂直于同一平面的两条直线互相平行( )×(1)平行于同一直线的两条直线互相平行( )√五、过程设计(三) 线面垂直性质定理的应用小牛试刀(1)若PA=PB=PC,则O是△ABC的 .PABC?O外心例4.关于三角形的四心问题 设O为三棱锥P—ABC的顶点P在底面上的射影.综合练习:(2)若PA=PB=PC,∠C=900,则O是AB的_____点.中PABC?O例4.关于三角形的四心问题综合练习:垂心EFPABC?O (3)若三条側棱两两互相垂直,则O是△ABC的 .例4.关于三角形的四心问题综合练习:EFPABC?O (5)若三条側棱与底面成相等的角,则O是△ABC的_____. 外心例4.关于三角形的四心问题综合练习:例1、已知直角△ABC所在平面外有一点P,且PA=PB=PC,D是斜边AB的中点,
求证:PD⊥平面ABC. 证明:PA=PB,D为AB中点
∴ PD⊥AB,连接CD,
∵D为Rt△ABC斜边的中点
∴ CD=AD, 又PA=PC,PD=PD
∴ △PAD≌△PCD 而PD⊥AB
∴ PD⊥CD, CD∩AB = D
∴PD⊥平面ABC例2、如图 平面α、β相交于PQ,
线段OA、OB分别垂直平面α、β,
求证:PQ⊥AB证明:∵OA⊥α PQ?α
∴ OA⊥PQ
OB⊥β, PQ?β
∴ OB⊥PQ
又OA∩OB=0
∴PQ⊥平面OAB
而AB?平面OAB
∴ PQ⊥ABSABCHSABCH1.如图,已知点M是菱形ABCD所在平面外一点,且MA=MC
求证:AC⊥平面BDMMABCDOABCD证明: 2. 在空间四边形ABCD中,AB=AD,CB=CD,
求证:对角线AC BD。 3.如图,圆O所在一平面为 ,AB是圆O 的直径,C 在圆周上, 且PA AC, PA AB,
求证:(1)PA BC
(2)BC 平面PAC典例 平面内有一个三角形ABC,平面外有一点P,自P向平面作斜线PA,PB,PC,且PA=PB=PC,若点O是△ABC的外心,求证:PO⊥平面ABC.【解】 如图所示,分别取AB,BC的中点D,E,连接PD,PE,OD,OE.
因为PA=PB=PC,
所以PD⊥AB,PE⊥BC,
因为O是△ABC的外心,
所以OD⊥AB,OE⊥BC,
又因为PD∩DO=D,OE∩PE=E,
所以AB⊥平面PDO,BC⊥平面PEO,
于是有AB⊥PO,BC⊥PO,AB∩BC=B,
从而推得PO⊥平面ABC.中外垂重心:三条中线的交点
垂心:三条高的交点
外心:三条垂直平分线的交点(到△三个顶点的距离相等)
内心:三角平分线的交点
中心:正△的重心、垂心、内心、外心重合的点巩固练习VABC直线与平面垂直的判定与性质 解题分析:解题小结:2018-10-23例1:如图,已知AC、AB分别是平面α的垂线
和斜线,C、B分别是垂足和斜足,a α,
a⊥BC.求证:a⊥AB. ACBaα射影垂直,斜线垂直2018-10-23例2:如图,∠BAC在平面α内,P为平面α外一
点,∠PAB=∠PAC.求证:点P在平面α上
的射影在∠BAC的平分线上. ACBPαOEF巩固练习1.平行四边形ABCD所在平面a外有一点P,且PA=PB=PC=PD,求证:点P与平行四边形对角线交点O的连线PO垂直于AB、AD.2018-10-23例2:如图,在棱长为1的正方体中.
(1)求B1D 与平面ABCD所成的角的正切;O(2)求A1C1 与平面ABC1D1所成的角;(3)求BB1 与平面A1BC1所成的角的正切.MH2018-10-23例5:⊿ABC的定点在平面α内,点A、C在平面
α的同侧,AB、BC与α所成角分别是300和
450.若AB=3,BC=4√2,AC=5,求AC
与平面α所成的角. AαBC2018-10-23例6:如图,P是正方形ABCD所在平面外一点,
PA⊥平面ABCD,AE ⊥ PD,PA=3AB.求
直线AC与平面ABE所成角的正弦值. PABCDE 【5】如图, AB为平面α的一条斜线, B为斜足,AO⊥平面α, 垂足为O, 直线BC在平面α内,已知∠ABC=60°,∠OBC=45°, 则斜线AB和平面α所成的角是_______.ACODBα45°设OB=2,补充练习引课我们知道,当直线和平面垂直时,该直线叫做平面的垂线。如果直线和平面不垂直,是不是也该给它取个名字呢?此时又该如何刻画直线和平面的这种关系呢?直线与平面所成的角1.平面的斜线如图,若一条直线PA和一个平面α相交,但不垂直,那么这条直线就叫做这个平面的斜线,斜线和平面的交点A叫做斜足。PA斜足斜线例1、如图,正方体ABCD-A1B1C1D1中,求
(1)直线A1B和平面 BCC1B1所成的角。
(2)直线A1B和平面A1B1CD所成的角。O例题示范,巩固新知分析:找出直线A1B在平面BCC1B1和平面A1B1CD内的射影,就可以求出A1B和平面BCC1B1和平面A1B1CD所成的角。阅读教科书P67上的解答过程HC与平面ABCD 所成的角是?BG和EA与平面ABCD所成的角 分别是?∠GBC与∠EAB∠HCDEC和EG与平面ABCD所成的角分别是?∠ACE练习:正方体ABCD-EFGH中
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影A1D1C1B1ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
2.如图:正方体ABCD-A1B1C1D1中,求:
(1)AB1在面BB1D1D中的射影
(2)AB1在面A1B1CD中的射影
(3)AB1在面CDD1C1中的射影ADCB巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB0o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB90o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB45o巩固练习
3.如图:正方体ABCD-A1B1C1D1中,求:
(1)A1C1与面ABCD所成的角
(2) A1C1与面BB1D1D所成的角
(3) A1C1与面BB1C1C所成的角
(4)A1C1与面ABC1D1所成的角ADCB30o巩固练习线线垂直相交垂直(共面垂直)异面垂直
