1.1 简单几何体 同步练习2(含答案)
文档属性
| 名称 | 1.1 简单几何体 同步练习2(含答案) | 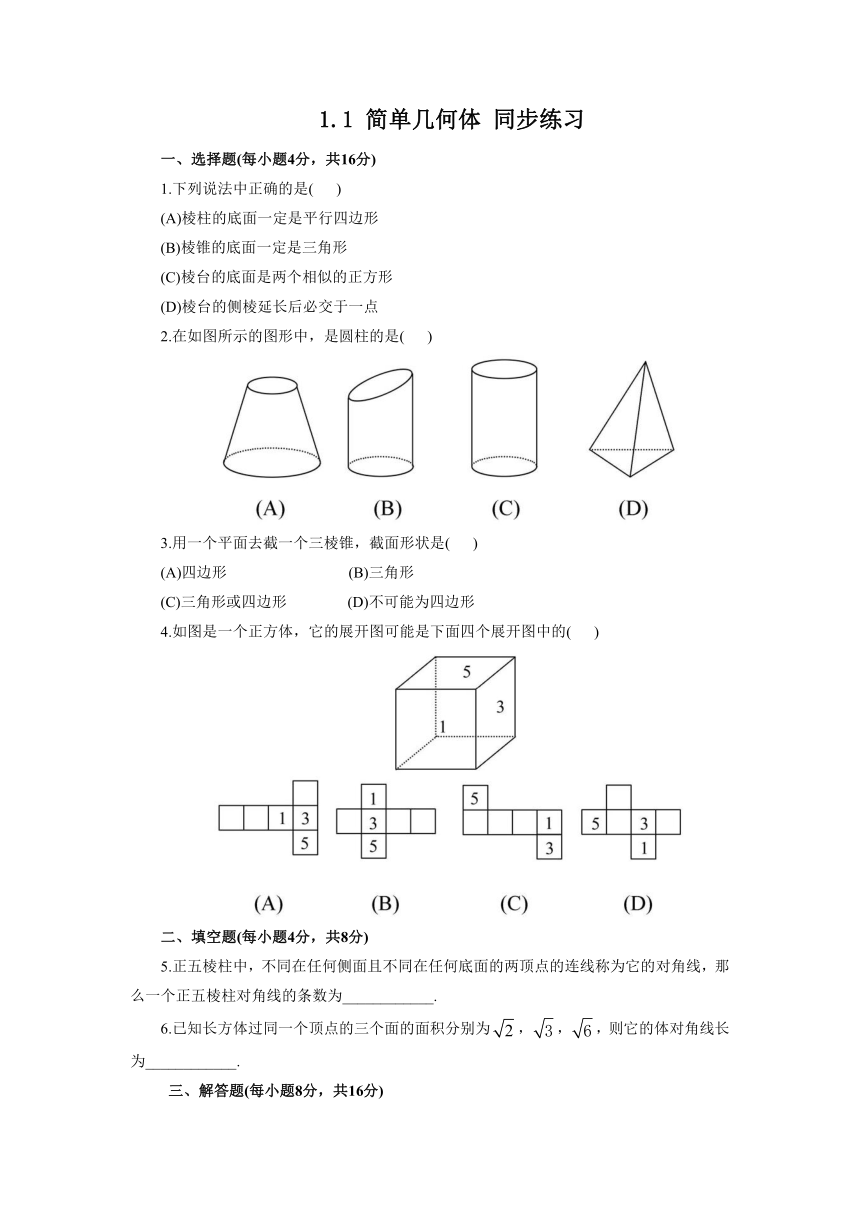 | |
| 格式 | zip | ||
| 文件大小 | 316.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 15:46:37 | ||
图片预览

文档简介
1.1
简单几何体
同步练习
一、选择题(每小题4分,共16分)
1.下列说法中正确的是(
)
(A)棱柱的底面一定是平行四边形
(B)棱锥的底面一定是三角形
(C)棱台的底面是两个相似的正方形
(D)棱台的侧棱延长后必交于一点
2.在如图所示的图形中,是圆柱的是(
)
3.用一个平面去截一个三棱锥,截面形状是(
)
(A)四边形
(B)三角形
(C)三角形或四边形
(D)不可能为四边形
4.如图是一个正方体,它的展开图可能是下面四个展开图中的(
)
二、填空题(每小题4分,共8分)
5.正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数为____________.
6.已知长方体过同一个顶点的三个面的面积分别为,,,则它的体对角线长为____________.
三、解答题(每小题8分,共16分)
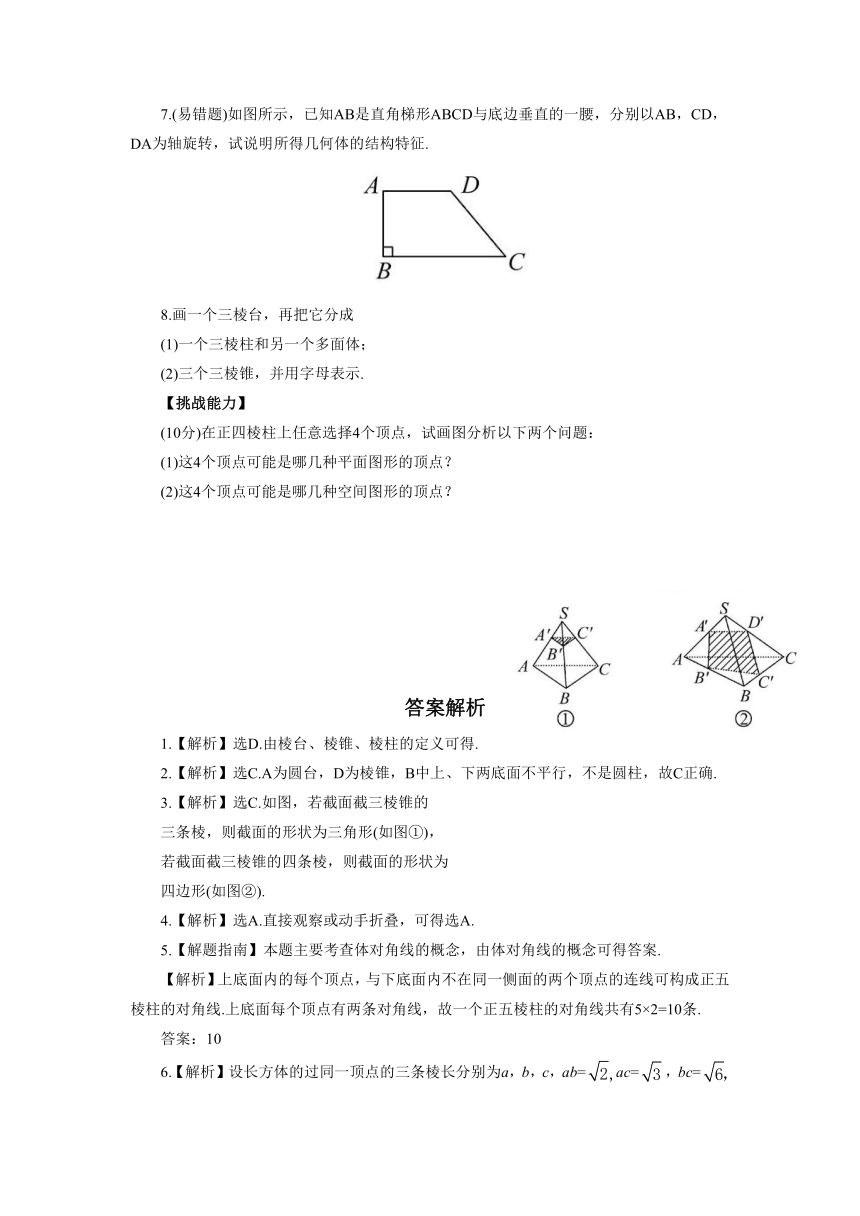
7.(易错题)如图所示,已知AB是直角梯形ABCD与底边垂直的一腰,分别以AB,CD,DA为轴旋转,试说明所得几何体的结构特征.
8.画一个三棱台,再把它分成
(1)一个三棱柱和另一个多面体;
(2)三个三棱锥,并用字母表示.
【挑战能力】
(10分)在正四棱柱上任意选择4个顶点,试画图分析以下两个问题:
(1)这4个顶点可能是哪几种平面图形的顶点?
(2)这4个顶点可能是哪几种空间图形的顶点?
答案解析
1.【解析】选D.由棱台、棱锥、棱柱的定义可得.
2.【解析】选C.A为圆台,D为棱锥,B中上、下两底面不平行,不是圆柱,故C正确.
3.【解析】选C.如图,若截面截三棱锥的
三条棱,则截面的形状为三角形(如图①),
若截面截三棱锥的四条棱,则截面的形状为
四边形(如图②).
4.【解析】选A.直接观察或动手折叠,可得选A.
5.【解题指南】本题主要考查体对角线的概念,由体对角线的概念可得答案.
【解析】上底面内的每个顶点,与下底面内不在同一侧面的两个顶点的连线可构成正五棱柱的对角线.上底面每个顶点有两条对角线,故一个正五棱柱的对角线共有5×2=10条.
答案:10
6.【解析】设长方体的过同一顶点的三条棱长分别为a,b,c,ab=ac=,bc=解之得a=1,b=c=,所以长方体的体对角线长为
答案
【方法技巧】巧化未知为已知
长方体棱长和体对角线长的关系公式为l=此公式的推导利用了长方体中体对角线与棱构成的直角三角形,体现了化立体几何问题为平面几何问题的思想方法,这种思想方法对于解决立体几何问题是十分重要的.
7.【解析】(1)以AB边为轴旋转所得的旋转体是圆台,如图(1)所示.
(2)以CD边为轴旋转所得几何体为:上部为圆锥,下部为圆台,再挖去一个小圆锥,如图(2)所示.
(3)以AD边为轴旋转得到几何体,它是一个圆柱上部挖去一个圆锥,如图(3)所示.
【误区警示】本题以CD为轴旋转所得的几何体易忽略挖去底面的小圆锥而出错.
8.【解析】画三棱台一定要利用三棱锥.
(1)如图①所示,三棱柱是棱柱A′B′C′-AB″C″.
(2)如图②所示,三个三棱锥分别是
A′-ABC,B′-A′BC,C′-A′B′C.
【挑战能力】
【解析】(1)这4个顶点可能是以下平面图形的顶点:矩形,正方形.
(2)这4个顶点可能是以下空间图形的顶点:
有三个面为直角三角形,一个面为等腰三角形的四面体(如图1,2);每个面都是等腰三角形的四面体(如图3);每个面都是直角三角形的四面体(如图4).
简单几何体
同步练习
一、选择题(每小题4分,共16分)
1.下列说法中正确的是(
)
(A)棱柱的底面一定是平行四边形
(B)棱锥的底面一定是三角形
(C)棱台的底面是两个相似的正方形
(D)棱台的侧棱延长后必交于一点
2.在如图所示的图形中,是圆柱的是(
)
3.用一个平面去截一个三棱锥,截面形状是(
)
(A)四边形
(B)三角形
(C)三角形或四边形
(D)不可能为四边形
4.如图是一个正方体,它的展开图可能是下面四个展开图中的(
)
二、填空题(每小题4分,共8分)
5.正五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个正五棱柱对角线的条数为____________.
6.已知长方体过同一个顶点的三个面的面积分别为,,,则它的体对角线长为____________.
三、解答题(每小题8分,共16分)
7.(易错题)如图所示,已知AB是直角梯形ABCD与底边垂直的一腰,分别以AB,CD,DA为轴旋转,试说明所得几何体的结构特征.
8.画一个三棱台,再把它分成
(1)一个三棱柱和另一个多面体;
(2)三个三棱锥,并用字母表示.
【挑战能力】
(10分)在正四棱柱上任意选择4个顶点,试画图分析以下两个问题:
(1)这4个顶点可能是哪几种平面图形的顶点?
(2)这4个顶点可能是哪几种空间图形的顶点?
答案解析
1.【解析】选D.由棱台、棱锥、棱柱的定义可得.
2.【解析】选C.A为圆台,D为棱锥,B中上、下两底面不平行,不是圆柱,故C正确.
3.【解析】选C.如图,若截面截三棱锥的
三条棱,则截面的形状为三角形(如图①),
若截面截三棱锥的四条棱,则截面的形状为
四边形(如图②).
4.【解析】选A.直接观察或动手折叠,可得选A.
5.【解题指南】本题主要考查体对角线的概念,由体对角线的概念可得答案.
【解析】上底面内的每个顶点,与下底面内不在同一侧面的两个顶点的连线可构成正五棱柱的对角线.上底面每个顶点有两条对角线,故一个正五棱柱的对角线共有5×2=10条.
答案:10
6.【解析】设长方体的过同一顶点的三条棱长分别为a,b,c,ab=ac=,bc=解之得a=1,b=c=,所以长方体的体对角线长为
答案
【方法技巧】巧化未知为已知
长方体棱长和体对角线长的关系公式为l=此公式的推导利用了长方体中体对角线与棱构成的直角三角形,体现了化立体几何问题为平面几何问题的思想方法,这种思想方法对于解决立体几何问题是十分重要的.
7.【解析】(1)以AB边为轴旋转所得的旋转体是圆台,如图(1)所示.
(2)以CD边为轴旋转所得几何体为:上部为圆锥,下部为圆台,再挖去一个小圆锥,如图(2)所示.
(3)以AD边为轴旋转得到几何体,它是一个圆柱上部挖去一个圆锥,如图(3)所示.
【误区警示】本题以CD为轴旋转所得的几何体易忽略挖去底面的小圆锥而出错.
8.【解析】画三棱台一定要利用三棱锥.
(1)如图①所示,三棱柱是棱柱A′B′C′-AB″C″.
(2)如图②所示,三个三棱锥分别是
A′-ABC,B′-A′BC,C′-A′B′C.
【挑战能力】
【解析】(1)这4个顶点可能是以下平面图形的顶点:矩形,正方形.
(2)这4个顶点可能是以下空间图形的顶点:
有三个面为直角三角形,一个面为等腰三角形的四面体(如图1,2);每个面都是等腰三角形的四面体(如图3);每个面都是直角三角形的四面体(如图4).
