1.1.1 简单旋转体 同步练习1(含答案)
文档属性
| 名称 | 1.1.1 简单旋转体 同步练习1(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 329.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 15:48:50 | ||
图片预览


文档简介
1.1.1
简单旋转体
同步练习
基础巩固
一、选择题
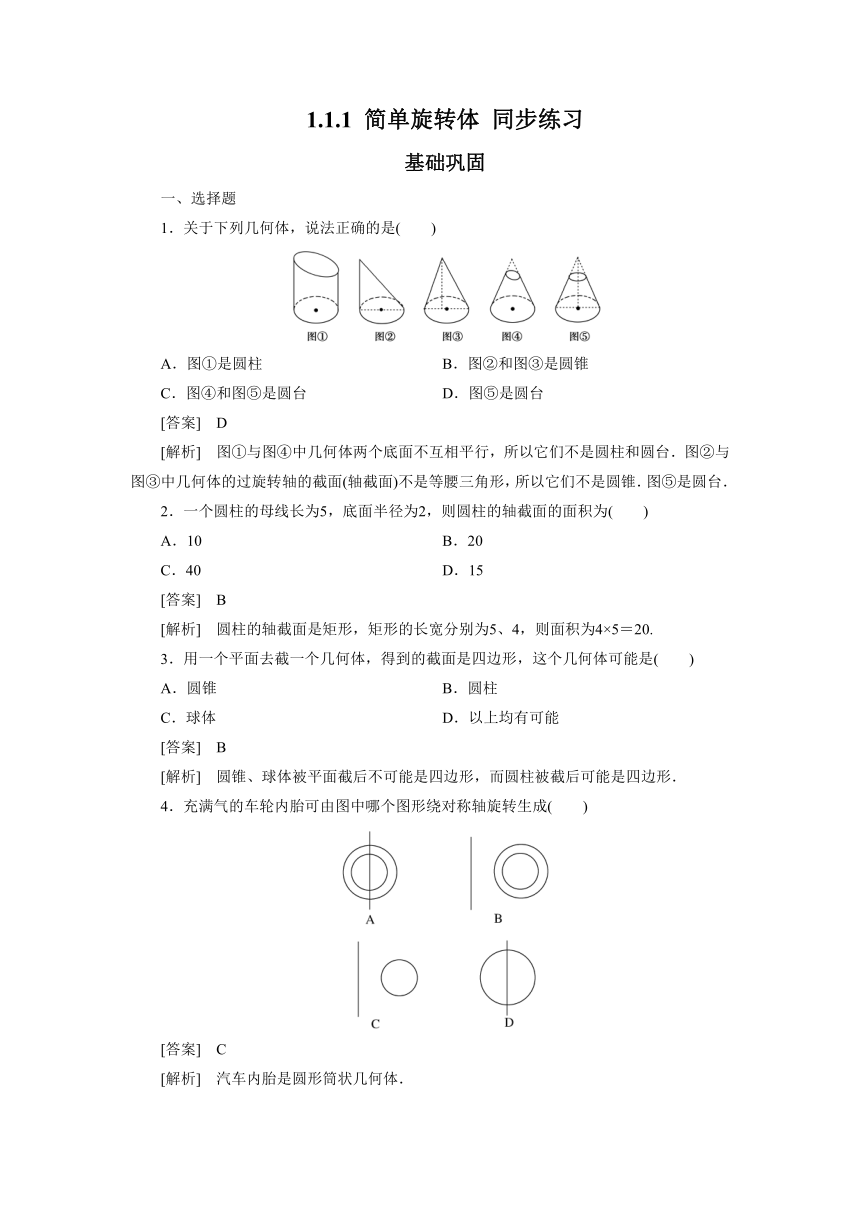
1.关于下列几何体,说法正确的是( )
A.图①是圆柱
B.图②和图③是圆锥
C.图④和图⑤是圆台
D.图⑤是圆台
[答案] D
[解析] 图①与图④中几何体两个底面不互相平行,所以它们不是圆柱和圆台.图②与图③中几何体的过旋转轴的截面(轴截面)不是等腰三角形,所以它们不是圆锥.图⑤是圆台.
2.一个圆柱的母线长为5,底面半径为2,则圆柱的轴截面的面积为( )
A.10
B.20
C.40
D.15
[答案] B
[解析] 圆柱的轴截面是矩形,矩形的长宽分别为5、4,则面积为4×5=20.
3.用一个平面去截一个几何体,得到的截面是四边形,这个几何体可能是( )
A.圆锥
B.圆柱
C.球体
D.以上均有可能
[答案] B
[解析] 圆锥、球体被平面截后不可能是四边形,而圆柱被截后可能是四边形.
4.充满气的车轮内胎可由图中哪个图形绕对称轴旋转生成( )
[答案] C
[解析] 汽车内胎是圆形筒状几何体.
5.一个正方体内有一个内切球,作正方体的对角面,所得截面图形是下图中的( )
[答案] B
[解析] 由组合体的结构特征知,球只与正方体的上、下底面相切,而与两侧棱相离.故正确答案为B.
6.已知球心到球的一个截面的距离为5,截面圆的半径为12,则球的半径为( )
A.13
B.12
C.5
D.
[答案] A
[解析] 设球的半径为R,则R==13.
二、填空题
7.已知圆台的轴与母线所在直线的夹角为45°,若上底面的半径为1,高为1,则圆台的下底面半径为________.
[答案] 2
[解析] 设下底面半径为r,则=tan45°,∴r=2.
8.有下列说法:
①球的半径是连接球面上任意一点和球心的线段;
②球的直径是球面上任意两点间的线段;
③用一个平面截一个球,得到的是一个圆;
④空间中到一定点距离相等的点的集合是一个球.
其中正确的有________.
[答案] ①
[解析] 球是半圆绕其直径所在的直线旋转,旋转面所围成的封闭的几何体,不难理解,半圆的直径就是球的直径,半圆的圆心就是球心,半圆的半径就是球的半径,因此①正确;如果球面上的两点连线经过球心,则这条线段就是球的直径,因此②错误;球是一个几何体,平面截它应得到一个面而不是一条曲线,所以③错误;空间中到一定点距离相等的点的集合是一个球面,而不是一个球体,所以④错误.
三、解答题
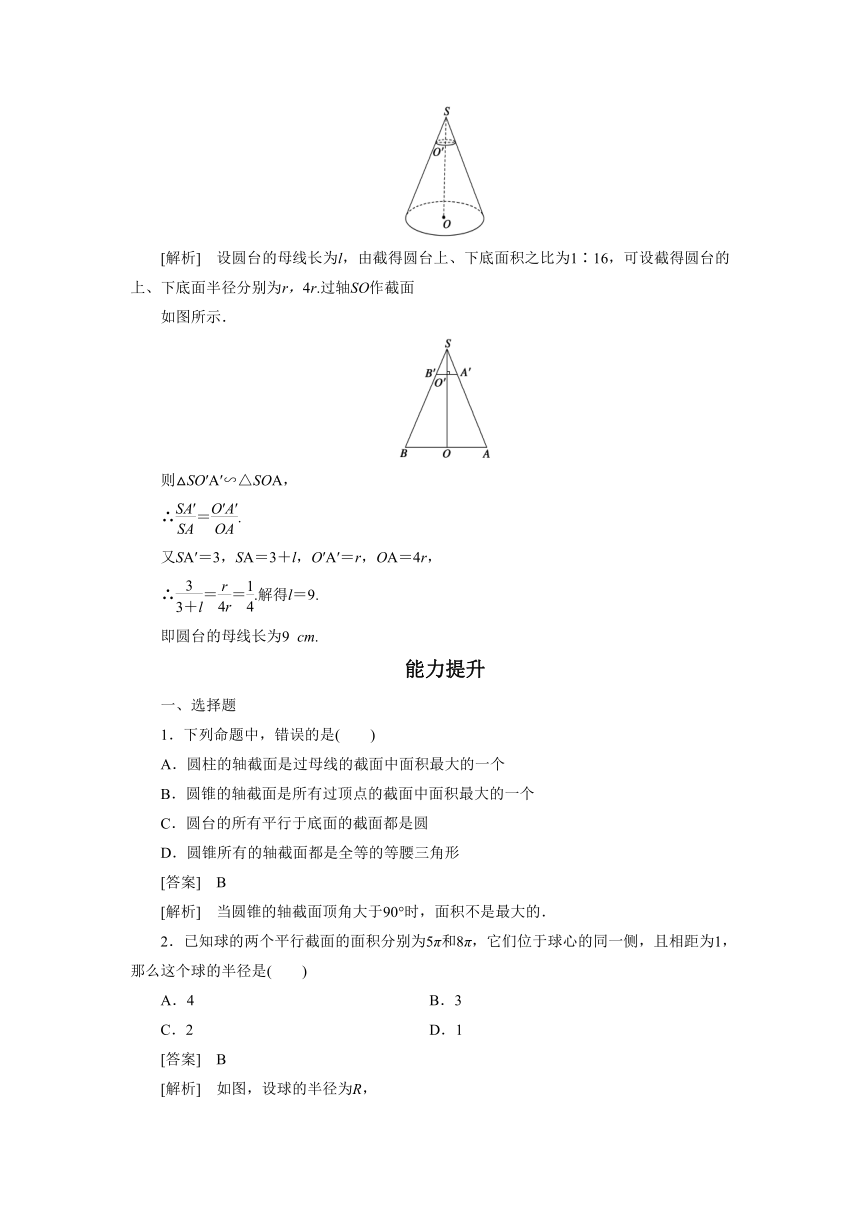
9.如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的小圆锥的母线长是3
cm,求圆台OO′的母线长.
[解析] 设圆台的母线长为l,由截得圆台上、下底面积之比为1∶16,可设截得圆台的上、下底面半径分别为r,4r.过轴SO作截面
如图所示.
则△SO′A′∽△SOA,
∴=.
又SA′=3,SA=3+l,O′A′=r,OA=4r,
∴==.解得l=9.
即圆台的母线长为9
cm.
能力提升
一、选择题
1.下列命题中,错误的是( )
A.圆柱的轴截面是过母线的截面中面积最大的一个
B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C.圆台的所有平行于底面的截面都是圆
D.圆锥所有的轴截面都是全等的等腰三角形
[答案] B
[解析] 当圆锥的轴截面顶角大于90°时,面积不是最大的.
2.已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧,且相距为1,那么这个球的半径是( )
A.4
B.3
C.2
D.1
[答案] B
[解析] 如图,设球的半径为R,
两截面圆的半径分别为r1,r2,
则πr=5π,πr=8π,
∴r1=,r2=2.
又O1O2=1,取OO2=x,
则有R2=5+(x+1)2,R2=8+x2,
∴5+(x+1)2=8+x2,
∴x=1,∴R=3.
二、填空题
3.若母线长是4的圆锥的轴截面的面积是8,则圆锥的高是________.
[答案] 2
[解析] 如图所示,设圆锥的底面半径为r,则圆锥的高是,
∵·2r·=8,
∴r=2.∴圆锥的高为=2.
4.已知圆锥母线与旋转轴所成的角为30°,母线的长为,则其底面面积为________.
[答案]
[解析] 如图所示,过圆锥的旋转轴作其轴截面ABC,设圆锥的底面半径为r.
∵△ABC为等腰三角形,
∴△ABO为直角三角形.
又∵∠BAO=30°,
∴BO=r=AB=.
∴底面圆O的面积为S=πr2=.
三、解答题
5.如图所示,已知AB是直角梯形ABCD与底边垂直的一腰.分别以AB,CD,DA为轴旋转,试说明所得几何体的结构特征.
[解析] (1)以AB边为轴旋转所得旋转体是圆台.如图(1)所示.
(2)以CD边为轴旋转所得旋转体为一组合体:上部为圆锥,下部为圆台,再挖去一个小圆锥,如图(2)所示.
(3)以AD边为轴旋转得到一个组合体,它是一个圆柱上部挖去一个圆锥.如图(3)所示.
6.轴截面为正三角形的圆锥叫作等边圆锥.已知某等边圆锥的轴截面面积为,求该圆锥的底面半径、高和母线长.
[解析] 如图△SAB为等边圆锥的轴截面,
设圆锥的底面半径为r,高为h,母线长为l,
则在轴截面△SAB中,
有OB=r,SO=h,SB=l,
且∠SBO=60°.
在直角△SOB中,h=r,l=2r,
所以S△SAB=×AB×SO=rh=r2,
根据题意得r2=,
解得r=1,所以l=2r=2,h=r=.
即该圆锥的底面半径为1,高为,母线长为2.
7.一个圆台的母线长为12cm,两底面面积分别为4πcm2和25πcm2,求:
(1)圆台的高;
(2)截得此圆台的圆锥的母线长.
[解析] (1)圆台的轴截面是等腰梯形ABCD(如图).
因为圆台上底面面积为4πcm2,
所以上底面半径为2cm.
又因为圆台下底面面积为25πcm2,
所以下底面半径为5cm,
所以高为AM==3(cm).
(2)延长BA,CD相交于点S,设截得此圆台的圆锥的母线长为l,
因为Rt△SAO1∽Rt△SBO,
所以=,即=,
解得l=20(cm),
即截得此圆台的圆锥的母线长为20cm.
简单旋转体
同步练习
基础巩固
一、选择题
1.关于下列几何体,说法正确的是( )
A.图①是圆柱
B.图②和图③是圆锥
C.图④和图⑤是圆台
D.图⑤是圆台
[答案] D
[解析] 图①与图④中几何体两个底面不互相平行,所以它们不是圆柱和圆台.图②与图③中几何体的过旋转轴的截面(轴截面)不是等腰三角形,所以它们不是圆锥.图⑤是圆台.
2.一个圆柱的母线长为5,底面半径为2,则圆柱的轴截面的面积为( )
A.10
B.20
C.40
D.15
[答案] B
[解析] 圆柱的轴截面是矩形,矩形的长宽分别为5、4,则面积为4×5=20.
3.用一个平面去截一个几何体,得到的截面是四边形,这个几何体可能是( )
A.圆锥
B.圆柱
C.球体
D.以上均有可能
[答案] B
[解析] 圆锥、球体被平面截后不可能是四边形,而圆柱被截后可能是四边形.
4.充满气的车轮内胎可由图中哪个图形绕对称轴旋转生成( )
[答案] C
[解析] 汽车内胎是圆形筒状几何体.
5.一个正方体内有一个内切球,作正方体的对角面,所得截面图形是下图中的( )
[答案] B
[解析] 由组合体的结构特征知,球只与正方体的上、下底面相切,而与两侧棱相离.故正确答案为B.
6.已知球心到球的一个截面的距离为5,截面圆的半径为12,则球的半径为( )
A.13
B.12
C.5
D.
[答案] A
[解析] 设球的半径为R,则R==13.
二、填空题
7.已知圆台的轴与母线所在直线的夹角为45°,若上底面的半径为1,高为1,则圆台的下底面半径为________.
[答案] 2
[解析] 设下底面半径为r,则=tan45°,∴r=2.
8.有下列说法:
①球的半径是连接球面上任意一点和球心的线段;
②球的直径是球面上任意两点间的线段;
③用一个平面截一个球,得到的是一个圆;
④空间中到一定点距离相等的点的集合是一个球.
其中正确的有________.
[答案] ①
[解析] 球是半圆绕其直径所在的直线旋转,旋转面所围成的封闭的几何体,不难理解,半圆的直径就是球的直径,半圆的圆心就是球心,半圆的半径就是球的半径,因此①正确;如果球面上的两点连线经过球心,则这条线段就是球的直径,因此②错误;球是一个几何体,平面截它应得到一个面而不是一条曲线,所以③错误;空间中到一定点距离相等的点的集合是一个球面,而不是一个球体,所以④错误.
三、解答题
9.如图所示,用一个平行于圆锥SO底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的小圆锥的母线长是3
cm,求圆台OO′的母线长.
[解析] 设圆台的母线长为l,由截得圆台上、下底面积之比为1∶16,可设截得圆台的上、下底面半径分别为r,4r.过轴SO作截面
如图所示.
则△SO′A′∽△SOA,
∴=.
又SA′=3,SA=3+l,O′A′=r,OA=4r,
∴==.解得l=9.
即圆台的母线长为9
cm.
能力提升
一、选择题
1.下列命题中,错误的是( )
A.圆柱的轴截面是过母线的截面中面积最大的一个
B.圆锥的轴截面是所有过顶点的截面中面积最大的一个
C.圆台的所有平行于底面的截面都是圆
D.圆锥所有的轴截面都是全等的等腰三角形
[答案] B
[解析] 当圆锥的轴截面顶角大于90°时,面积不是最大的.
2.已知球的两个平行截面的面积分别为5π和8π,它们位于球心的同一侧,且相距为1,那么这个球的半径是( )
A.4
B.3
C.2
D.1
[答案] B
[解析] 如图,设球的半径为R,
两截面圆的半径分别为r1,r2,
则πr=5π,πr=8π,
∴r1=,r2=2.
又O1O2=1,取OO2=x,
则有R2=5+(x+1)2,R2=8+x2,
∴5+(x+1)2=8+x2,
∴x=1,∴R=3.
二、填空题
3.若母线长是4的圆锥的轴截面的面积是8,则圆锥的高是________.
[答案] 2
[解析] 如图所示,设圆锥的底面半径为r,则圆锥的高是,
∵·2r·=8,
∴r=2.∴圆锥的高为=2.
4.已知圆锥母线与旋转轴所成的角为30°,母线的长为,则其底面面积为________.
[答案]
[解析] 如图所示,过圆锥的旋转轴作其轴截面ABC,设圆锥的底面半径为r.
∵△ABC为等腰三角形,
∴△ABO为直角三角形.
又∵∠BAO=30°,
∴BO=r=AB=.
∴底面圆O的面积为S=πr2=.
三、解答题
5.如图所示,已知AB是直角梯形ABCD与底边垂直的一腰.分别以AB,CD,DA为轴旋转,试说明所得几何体的结构特征.
[解析] (1)以AB边为轴旋转所得旋转体是圆台.如图(1)所示.
(2)以CD边为轴旋转所得旋转体为一组合体:上部为圆锥,下部为圆台,再挖去一个小圆锥,如图(2)所示.
(3)以AD边为轴旋转得到一个组合体,它是一个圆柱上部挖去一个圆锥.如图(3)所示.
6.轴截面为正三角形的圆锥叫作等边圆锥.已知某等边圆锥的轴截面面积为,求该圆锥的底面半径、高和母线长.
[解析] 如图△SAB为等边圆锥的轴截面,
设圆锥的底面半径为r,高为h,母线长为l,
则在轴截面△SAB中,
有OB=r,SO=h,SB=l,
且∠SBO=60°.
在直角△SOB中,h=r,l=2r,
所以S△SAB=×AB×SO=rh=r2,
根据题意得r2=,
解得r=1,所以l=2r=2,h=r=.
即该圆锥的底面半径为1,高为,母线长为2.
7.一个圆台的母线长为12cm,两底面面积分别为4πcm2和25πcm2,求:
(1)圆台的高;
(2)截得此圆台的圆锥的母线长.
[解析] (1)圆台的轴截面是等腰梯形ABCD(如图).
因为圆台上底面面积为4πcm2,
所以上底面半径为2cm.
又因为圆台下底面面积为25πcm2,
所以下底面半径为5cm,
所以高为AM==3(cm).
(2)延长BA,CD相交于点S,设截得此圆台的圆锥的母线长为l,
因为Rt△SAO1∽Rt△SBO,
所以=,即=,
解得l=20(cm),
即截得此圆台的圆锥的母线长为20cm.
