1.2 直观图 同步练习2(含答案)
图片预览
文档简介
1.2
直观图
同步练习
1.有下列说法:
①从投影的角度看,斜二测画法画的直观图是在平行投影下画出来的空间图形;②平行投影的投影线互相平行,中心投影的投影线相交于一点;③空间图形经过中心投影后,直线仍为直线,但平行线可能变成相交的直线;④空间几何体在平行投影与中心投影下有不同的表现形式.
其中正确的命题有( ).
A.1个
B.2个
C.3个
D.4个
2.下列说法正确的是( ).
A.互相垂直的两条直线的直观图一定是互相垂直的两条直线
B.梯形的直观图可能是平行四边形
C.矩形的直观图可能是梯形
D.正方形的直观图可能是平行四边形
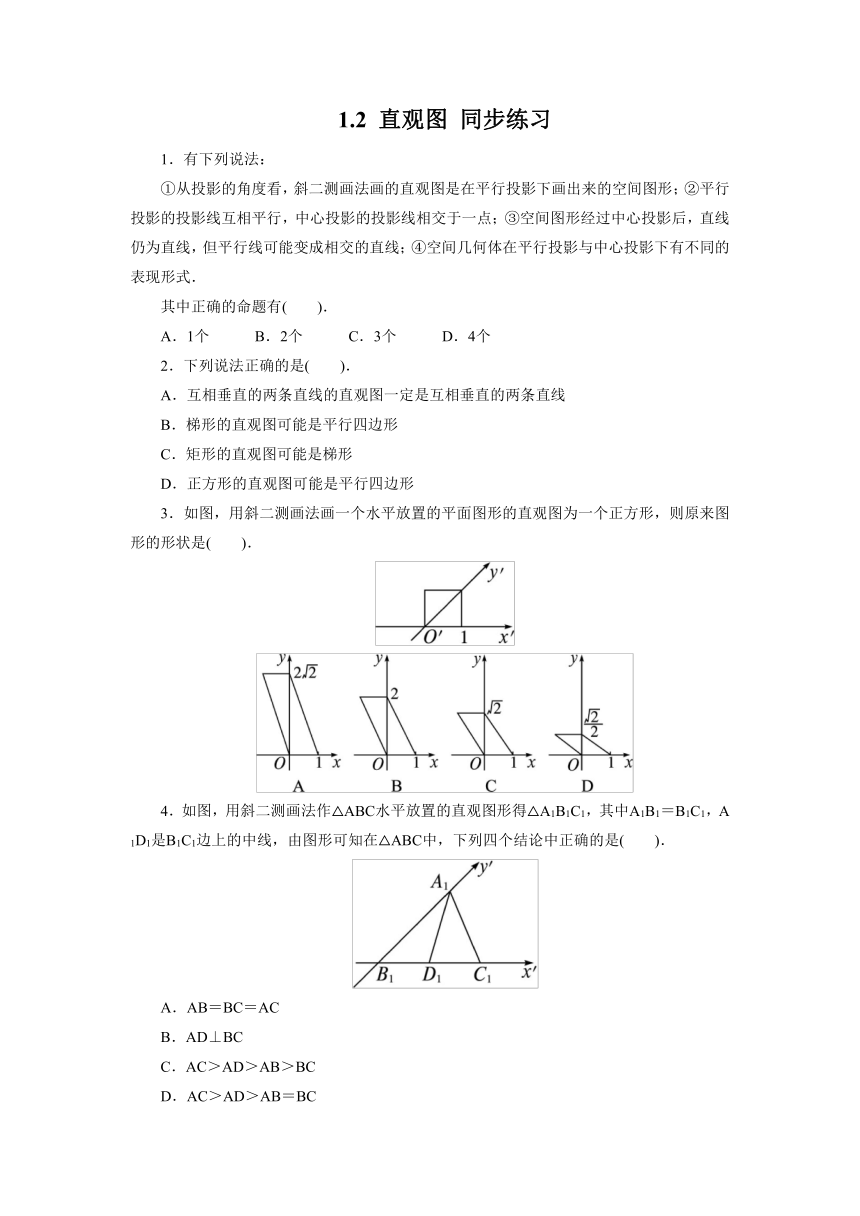
3.如图,用斜二测画法画一个水平放置的平面图形的直观图为一个正方形,则原来图形的形状是( ).
4.如图,用斜二测画法作△ABC水平放置的直观图形得△A1B1C1,其中A1B1=B1C1,A1D1是B1C1边上的中线,由图形可知在△ABC中,下列四个结论中正确的是( ).
A.AB=BC=AC
B.AD⊥BC
C.AC>AD>AB>BC
D.AC>AD>AB=BC
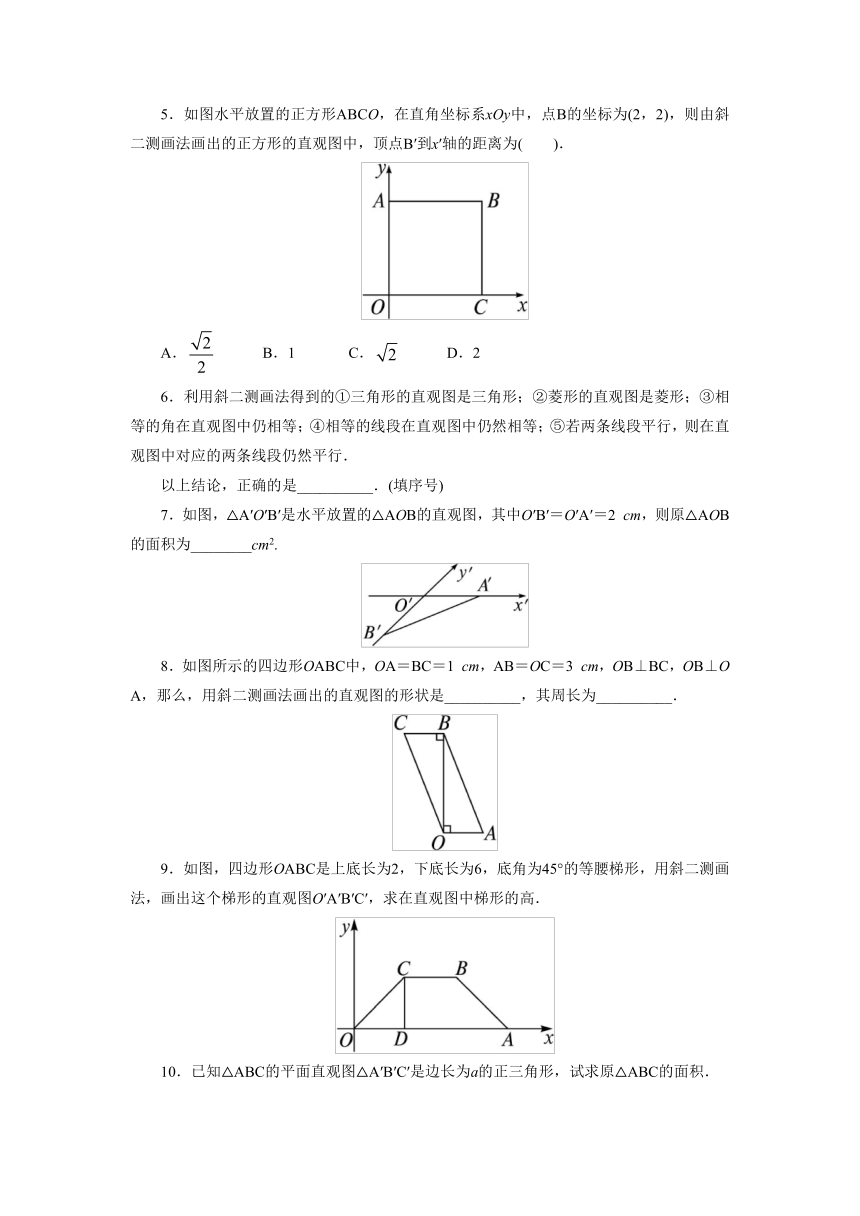
5.如图水平放置的正方形ABCO,在直角坐标系xOy中,点B的坐标为(2,2),则由斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为( ).
A.
B.1
C.
D.2
6.利用斜二测画法得到的①三角形的直观图是三角形;②菱形的直观图是菱形;③相等的角在直观图中仍相等;④相等的线段在直观图中仍然相等;⑤若两条线段平行,则在直观图中对应的两条线段仍然平行.
以上结论,正确的是__________.(填序号)
7.如图,△A′O′B′是水平放置的△AOB的直观图,其中O′B′=O′A′=2
cm,则原△AOB的面积为________cm2.
8.如图所示的四边形OABC中,OA=BC=1
cm,AB=OC=3
cm,OB⊥BC,OB⊥OA,那么,用斜二测画法画出的直观图的形状是__________,其周长为__________.
9.如图,四边形OABC是上底长为2,下底长为6,底角为45°的等腰梯形,用斜二测画法,画出这个梯形的直观图O′A′B′C′,求在直观图中梯形的高.
10.已知△ABC的平面直观图△A′B′C′是边长为a的正三角形,试求原△ABC的面积.
参考答案
1答案:D 解析:利用平行投影与中心投影的概念逐一判断,以上四句话都正确.
2答案:D
3答案:A 解析:直观图中正方形的对角线长(即在y′轴上的部分)为,因此在原图形中应在y轴上且长为.故选A.
3答案:C 解析:画出△A1B1C1的原图△ABC即可得.
5答案:A 解析:如图,由斜二测画法可知,在新坐标系x′O′y′中,B′C′=1,∠x′C′B′=45°,过B′作x′轴的垂线,垂足为D,在Rt△B′DC′中,B′D=B′C′sin
45°=1×=.
6答案:①⑤
7答案:4 解析:根据斜二测画法的规则可知,
△AOB为直角三角形,即∠AOB=90°,OA=O′A′=2
cm,OB=2O′B′=4
cm,
∴S△AOB=×OA×OB=×2×4=4(cm2).
8答案:正方形 4
cm 解析:原图形中,OB=
(cm),且OA⊥OB,那么在直观图中,∠A′O′B′=45°,O′B′=OB=
(cm),又B′C′=1
cm,所以四边形O′A′B′C′必为正方形,边长为1
cm,其周长为4
cm.
9答案:解:按斜二测画法得梯形的直观图O′A′B′C′,如下图所示,原图形中梯形的高CD=2,在直观图中C′D′=1,且∠C′D′A′=45°,作C′E′垂直x′轴于E′,则C′E′即为直观图中梯形的高,那么C′E′=C′D′sin
45°=.
10答案:解:在△A′B′C′所在的平面上建立坐标系x′O′y′,使x′轴,y′轴成45°角,如图(甲),建立直角坐标系xOy,使x轴,y轴成90°角,如图(乙).
∵△A′B′C′为正三角形,
∴△A′B′C′的高|A′D′|=.
∴|O′A′|=|A′D′|=.
∵在直观图中平行于y′轴的线段为原线段的一半,平行于x′轴的线段与原线段等长.
∴在原图中,|OA|=2|O′A′|=,|BC|=|B′C′|=a,
∴S△ABC=|BC|·|OA|=.
直观图
同步练习
1.有下列说法:
①从投影的角度看,斜二测画法画的直观图是在平行投影下画出来的空间图形;②平行投影的投影线互相平行,中心投影的投影线相交于一点;③空间图形经过中心投影后,直线仍为直线,但平行线可能变成相交的直线;④空间几何体在平行投影与中心投影下有不同的表现形式.
其中正确的命题有( ).
A.1个
B.2个
C.3个
D.4个
2.下列说法正确的是( ).
A.互相垂直的两条直线的直观图一定是互相垂直的两条直线
B.梯形的直观图可能是平行四边形
C.矩形的直观图可能是梯形
D.正方形的直观图可能是平行四边形
3.如图,用斜二测画法画一个水平放置的平面图形的直观图为一个正方形,则原来图形的形状是( ).
4.如图,用斜二测画法作△ABC水平放置的直观图形得△A1B1C1,其中A1B1=B1C1,A1D1是B1C1边上的中线,由图形可知在△ABC中,下列四个结论中正确的是( ).
A.AB=BC=AC
B.AD⊥BC
C.AC>AD>AB>BC
D.AC>AD>AB=BC
5.如图水平放置的正方形ABCO,在直角坐标系xOy中,点B的坐标为(2,2),则由斜二测画法画出的正方形的直观图中,顶点B′到x′轴的距离为( ).
A.
B.1
C.
D.2
6.利用斜二测画法得到的①三角形的直观图是三角形;②菱形的直观图是菱形;③相等的角在直观图中仍相等;④相等的线段在直观图中仍然相等;⑤若两条线段平行,则在直观图中对应的两条线段仍然平行.
以上结论,正确的是__________.(填序号)
7.如图,△A′O′B′是水平放置的△AOB的直观图,其中O′B′=O′A′=2
cm,则原△AOB的面积为________cm2.
8.如图所示的四边形OABC中,OA=BC=1
cm,AB=OC=3
cm,OB⊥BC,OB⊥OA,那么,用斜二测画法画出的直观图的形状是__________,其周长为__________.
9.如图,四边形OABC是上底长为2,下底长为6,底角为45°的等腰梯形,用斜二测画法,画出这个梯形的直观图O′A′B′C′,求在直观图中梯形的高.
10.已知△ABC的平面直观图△A′B′C′是边长为a的正三角形,试求原△ABC的面积.
参考答案
1答案:D 解析:利用平行投影与中心投影的概念逐一判断,以上四句话都正确.
2答案:D
3答案:A 解析:直观图中正方形的对角线长(即在y′轴上的部分)为,因此在原图形中应在y轴上且长为.故选A.
3答案:C 解析:画出△A1B1C1的原图△ABC即可得.
5答案:A 解析:如图,由斜二测画法可知,在新坐标系x′O′y′中,B′C′=1,∠x′C′B′=45°,过B′作x′轴的垂线,垂足为D,在Rt△B′DC′中,B′D=B′C′sin
45°=1×=.
6答案:①⑤
7答案:4 解析:根据斜二测画法的规则可知,
△AOB为直角三角形,即∠AOB=90°,OA=O′A′=2
cm,OB=2O′B′=4
cm,
∴S△AOB=×OA×OB=×2×4=4(cm2).
8答案:正方形 4
cm 解析:原图形中,OB=
(cm),且OA⊥OB,那么在直观图中,∠A′O′B′=45°,O′B′=OB=
(cm),又B′C′=1
cm,所以四边形O′A′B′C′必为正方形,边长为1
cm,其周长为4
cm.
9答案:解:按斜二测画法得梯形的直观图O′A′B′C′,如下图所示,原图形中梯形的高CD=2,在直观图中C′D′=1,且∠C′D′A′=45°,作C′E′垂直x′轴于E′,则C′E′即为直观图中梯形的高,那么C′E′=C′D′sin
45°=.
10答案:解:在△A′B′C′所在的平面上建立坐标系x′O′y′,使x′轴,y′轴成45°角,如图(甲),建立直角坐标系xOy,使x轴,y轴成90°角,如图(乙).
∵△A′B′C′为正三角形,
∴△A′B′C′的高|A′D′|=.
∴|O′A′|=|A′D′|=.
∵在直观图中平行于y′轴的线段为原线段的一半,平行于x′轴的线段与原线段等长.
∴在原图中,|OA|=2|O′A′|=,|BC|=|B′C′|=a,
∴S△ABC=|BC|·|OA|=.
