1.3 三视图 教案
图片预览



文档简介
1.3
三视图
教案
●三维目标
1.知识与技能
(1)了解空间几何体的不同表示形式.(2)理解画三视图应遵循的规则,能画出简单组合体的三视图.
2.过程与方法
通过画三视图,培养学生的画图、识图能力.
3.情感、态度与价值观
提高学生空间想象力,体会三视图的作用.
●重点难点
重点:画出简单组合体的三视图.
难点:识别三视图所表示的空间几何体.
教学时要强调学生动手画三视图,通过对照组合体与三视图学会识别两者之间的关系.
●教学建议
本节内容是在学习了直观图之后对立体几何图形的进一步深化,也是对初中学过的基本几何体的三视图的直接延伸.教学时,教师要引导学生自己动手作图,画出简单空间图形(长方体、球、圆柱、锥等)的三视图,让学生在动手实践的过程中学会三视图的作法,体会三视图的作用,对于简单几何体的组合体,在作三视图之前应当提醒学生细心观察,认识了它的基本结构特征后,动手作图,通过三视图的学习,进一步丰富学生的空间想象力.
●教学流程
通过回顾初中学过的简单几何体的三视图引出本节课知识 通过例1及互动探究使学生进一步掌握简单几何体的三视图的画法 通过例2及变式训练,使学生掌握简单组合体的三视图的画法 通过例3及变式训练,使学生掌握由三视图还原实物图 归纳整理进行课堂小结,整体认识本节所学知识 完成当堂双基达标,巩固所学知识,并进行矫正
课标解读
1.了解空间几何体的不同表示形式.2.理解画三视图应遵循的规则.3.能画出简单组合体的三视图(重点).4.能识别三视图所表示的立体模型,并能画出它们的实物草图.(难点)
知识1
三视图
【问题导思】
在初中,我们学习了正方体、长方体、圆柱、圆锥、球的三视图,回忆三视图包含哪些图?
【提示】 主视图、左视图、俯视图.
1.特点:主、俯视图长对正;主、左视图高平齐;俯、左视图宽相等,前后对应.
2.画三视图时的注意事项:(1)主、俯视图长对正;主、左视图高平齐;俯、左视图宽相等,前后对应.(2)在三视图中,需要画出所有的轮廓线,其中,视线所见的轮廓
线画实线,看不见的轮廓线画虚线.③同一物体放置的位置不同,所画的三视图可能不同.
知识2
组合体
【问题导思】
日常生活中,我们遇到的几何体很多是组合体,如螺丝帽,矿泉水瓶等.(1)螺丝帽的俯视图是怎样的平面图形?(2)矿泉水瓶的主视图是怎样的平面图形?(3)组合体的三视图都完全不一样吗?
【提示】 (1)一个正六边形和中间一个圆.
(2)如图:
(3)不一定,例如矿泉水瓶的主视图和左视图一样.
1.定义:由基本几何体生成的几何体叫作组合体.
2.两种基本形式:一种是将基本几何体拼接成组合体;另一种是从基本几何体中切掉或挖掉部分构成组何体.
类型1
简单几何体的三视图
例1 画出如图1-3-1所示的几何体的三视图.
图1-3-1
【思路探究】 观察图形→确定方向→画三视图
【自主解答】 三视图如图所示:
规律方法
1.本题在画主视图与左视图时,易出现直接画成长方形的错误,导致这种错误的原因是对画三视图的规则理解不清.
2.在画三视图时,要想象几何体的后面、右面、下面各有一个屏幕,一组平行光线分别从前面、左面、上面垂直照射,我们画的是影子的轮廓,再验证几何体的轮廓线,看到的画实线,不能看到的画虚线.
互动探究
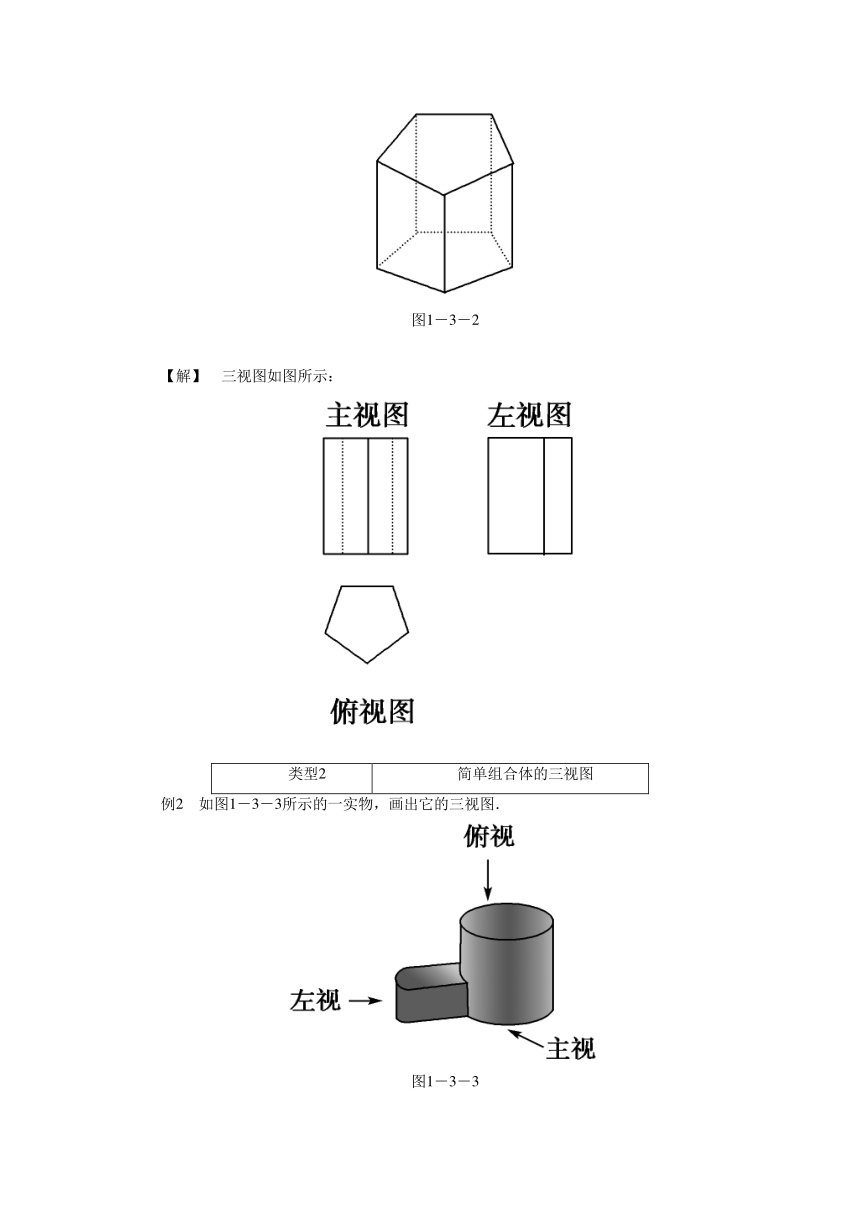
将本例中的正六棱柱换成如图1-3-2所示的正五棱柱呢?
图1-3-2
【解】 三视图如图所示:
类型2
简单组合体的三视图
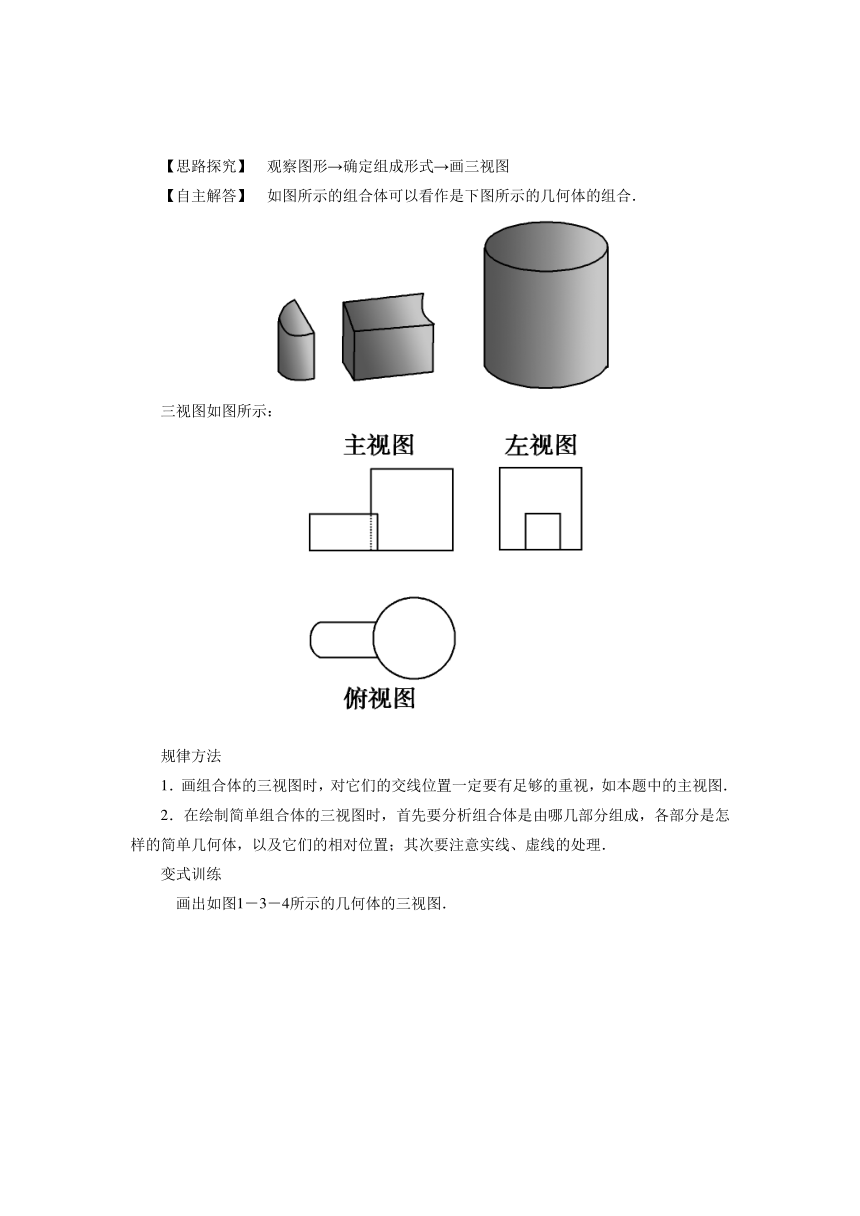
例2 如图1-3-3所示的一实物,画出它的三视图.
图1-3-3
【思路探究】 观察图形→确定组成形式→画三视图
【自主解答】 如图所示的组合体可以看作是下图所示的几何体的组合.
三视图如图所示:
规律方法
1.画组合体的三视图时,对它们的交线位置一定要有足够的重视,如本题中的主视图.
2.在绘制简单组合体的三视图时,首先要分析组合体是由哪几部分组成,各部分是怎样的简单几何体,以及它们的相对位置;其次要注意实线、虚线的处理.
变式训练
画出如图1-3-4所示的几何体的三视图.
图1-3-4
【解】 三视图如图所示.
类型3
由三视图还原实物直观图
例3 如图1-3-5是某几何体的三视图,想象该几何体的结构特征,并画出该几何体的实物草图.
图1-3-5
【思路探究】 (1)哪些几何体的主视图是长方形?
(2)哪些几何体的左视图是长方形?
(3)哪些几何体的俯视图是圆?
【自主解答】 由于俯视图含有一个圆和一个四边形,则该几何体是由旋转体和多面体拼接而成的组合体,结合主视图和左视图可知,该几何体的上面是一个圆柱,下面是一个四棱柱.该几何体的实物草图如图所示.
规律方法
1.由三视图还原实物直观图的步骤
(1)看俯视图:判断几何体是多面体还是旋转体;确定几何体在前后左右方向所占空间;
(2)看主视图、左视图:联想常见几何体,从实虚线变化、几何体组成方式等角度判断结构特征;
(3)画直观图:由几何体的结构特征画出直观图.
2.看图和想图是两个重要的步骤,“想”寓于“看”中,形体分析的看图方法是解决此类问题的常用方法.
变式训练
根据如图1-3-6三视图想象该几何体的结构特征,并画出该几何体的实物草图.
图1-3-6
【解】 实物草图如下:
忽视三视图的规则致误
典例 画出如图1-3-7的物体的三视图.
图1-3-7
【错解】
【错因分析】 三视图出现多处错误.首先,主视图和左视图的高应该是相同的,而所画的视图没有做到这一点;其次,左视图的宽应该和俯视图的高一致,这一点也没有做到;再次,主视图的长与俯视图的长应对齐,这点还是没有做到;最后,图中有一条看不到的棱应该用虚线表示出来,所以答案存在多处错误.
【防范措施】 注意画三视图的规则,即这三者之间的等量关系,再注意虚、实线的区分.
【正解】 如图所示.
1.对于画几何体的三视图,要实虚线分清,可以解释为“眼见为实,不见为虚”.对于同一物体放置的位置不同,所画的三视图可能不同.
2.对于画简单组合体的三视图,要先弄清由哪几个基本几何体组合而成,并注意它们的组成方式,特别是它们的交线位置.
3.对于还原组合体,需要综合主视图、左视图、俯视图的特征,确定分界线,找出组成组合体的简单几何体,再将组合体还原,其中确定分界线是正确还原的关键.
1.下列各项不属于三视图的是( )
A.主视图 B.左视图
C.后视图
D.俯视图
【解析】 三视图指的是主视图、左视图、俯视图.故选C.
【答案】 C
2.图1-3-8所示的圆锥的左视图是( )
图1-3-8
【解析】 此圆锥的左视图为圆,顶点在圆心处,故C正确.
【答案】 C
3.图1-3-9中三视图所表示物体的形状为______.
图1-3-9
【解析】 图中三视图所表示物体的形状为圆柱.
【答案】 圆柱
4.画出如图1-3-10所示几何体的三视图.
图1-3-10
【解】
一、选择题
1.对于几何体的三视图,下列说法正确的是( )
A.主视图反映物体的长和高
B.俯视图反映物体的长和高
C.如果一个几何体的主视图和左视图都是等腰梯形,则这个几何体是圆台
D.如果一个几何体的三视图都为圆,则此几何体为圆柱
【解析】 三视图中的主视图,左视图,俯视图分别反映物体的长、高,宽、高,长、宽,因此A正确,B错误;C描述的几何体还可能为正四棱台;D选项描述的几何体是球.
【答案】 A
2.已知某空间几何体的三视图如图1-3-11所示,则此几何体为( )
图1-3-11
A.圆台 B.四棱锥
C.四棱柱
D.四棱台
【解析】 由主视图和左视图可以判断一定的棱台或圆台,又由俯视图可知一定为棱台且为四棱台.
【答案】 D
3.找出图1-3-12中三视图所对应的实物图形是( )
图1-3-12
【解析】 由三视图的作法易知实物图形应为C.
【答案】 C
图1-3-13
4.一个去掉一角的长方体的直观图如图1-3-13所示,关于它的三视图,下列画法正确的是( )
A.它的主视图是:
B.它的主视图是:
C.它的左视图是:
D.它的俯视图是:
【解析】 抓住几何体的结构特征,结合三视图的画法可知A正确,左视图框内应是一虚斜线,俯视图中的虚线应为实线.
【答案】 A
5.一个简单几何体的主视图、左视图如图1-3-14所示,则其俯视图不可能为:①长方形;②正方形;③圆;④椭圆.
图1-3-14
其中正确的是( )
A.①②
B.②③
C.③④
D.①④
【解析】 若俯视图为正方形或圆时,主视图和左视图中矩形的宽应该相等,故②③不可能.
【答案】 B
二、填空题
6.某物体的实物图如图(甲)所示,在其三视图中,图①是________;图②是________;图③是________.
图1-3-15
【解析】 根据三视图的特点知①是主视图,②是俯视图,③是左视图.
【答案】 主视图 俯视图 左视图
7.如图1-3-16所示的三视图代表的立体图形是________.
图1-3-16
【解析】 由三视图知此几何体为一个正六棱锥.
【答案】 正六棱锥
8.如图1-3-17所示是一个圆锥的三视图,则该圆锥的高为______cm.
图1-3-17
【解析】 由三视图知,圆锥的母线长为3
cm,底面圆的直径为3
cm,所以圆锥的轴截面也是边长为3
cm的等边三角形,所以圆锥的高为=(cm).
【答案】
三、解答题
9.给出下面一个几何体,根据要求画出它的三视图:
图1-3-18
【解】 该几何体的三视图形状如下:
10.某座楼由相同的若干个房间组成,该楼的三视图如图1-3-19.
图1-3-19
问:(1)该楼有几层?从前往后最多要走过几个房间?
(2)最高一层的房间在什么位置?该楼最多有几个房间?
【解】 (1)该楼共有3层,可以从主视图和左视图中看出;从前往后最多要走过3个房间,可以从俯视图中看出.
(2)最高一层的房间在左后方,可以从左视图中看出.楼的大致形状如图所示,最多有10个房间.
11.如图1-3-20是一个空间几何体的三视图,其中主视图和左视图都是边长为2的正三角形,俯视图是一个正方形.
图1-3-20
(1)在给定的直角坐标系中作出这个几何体的直观图(不写作法);
(2)求这个几何体的高.
【解】 (1)直观图如图.
(2)这个几何体是一个正四棱锥,它的底面边长为2,高在正视图(或左视图)中可求,高h=2sin
60°=.
备选例题
画出下列几何体的三视图(阴影面为主视面).
【思路探究】 有了主视面,根据三视图特点画出三视图.
【自主解答】 三视图如图.
规律方法
画组合体的三视图时,首先要确定主视、左视和俯视的方向,然后从三个方向观察组合体的轮廓线,还要搞清楚组合体是由哪几种基本几何体组成的,并注意各基本几何体的组成方式及组接位置,其组接的交线往往又是组合体的轮廓线,被挡住的要画成虚线.
备选变式
画出如图所示的组合体的三视图.(阴影部分为主视面,尺寸不作严格要求)
【解】 这个组合体的三视图如下:
三视图
教案
●三维目标
1.知识与技能
(1)了解空间几何体的不同表示形式.(2)理解画三视图应遵循的规则,能画出简单组合体的三视图.
2.过程与方法
通过画三视图,培养学生的画图、识图能力.
3.情感、态度与价值观
提高学生空间想象力,体会三视图的作用.
●重点难点
重点:画出简单组合体的三视图.
难点:识别三视图所表示的空间几何体.
教学时要强调学生动手画三视图,通过对照组合体与三视图学会识别两者之间的关系.
●教学建议
本节内容是在学习了直观图之后对立体几何图形的进一步深化,也是对初中学过的基本几何体的三视图的直接延伸.教学时,教师要引导学生自己动手作图,画出简单空间图形(长方体、球、圆柱、锥等)的三视图,让学生在动手实践的过程中学会三视图的作法,体会三视图的作用,对于简单几何体的组合体,在作三视图之前应当提醒学生细心观察,认识了它的基本结构特征后,动手作图,通过三视图的学习,进一步丰富学生的空间想象力.
●教学流程
通过回顾初中学过的简单几何体的三视图引出本节课知识 通过例1及互动探究使学生进一步掌握简单几何体的三视图的画法 通过例2及变式训练,使学生掌握简单组合体的三视图的画法 通过例3及变式训练,使学生掌握由三视图还原实物图 归纳整理进行课堂小结,整体认识本节所学知识 完成当堂双基达标,巩固所学知识,并进行矫正
课标解读
1.了解空间几何体的不同表示形式.2.理解画三视图应遵循的规则.3.能画出简单组合体的三视图(重点).4.能识别三视图所表示的立体模型,并能画出它们的实物草图.(难点)
知识1
三视图
【问题导思】
在初中,我们学习了正方体、长方体、圆柱、圆锥、球的三视图,回忆三视图包含哪些图?
【提示】 主视图、左视图、俯视图.
1.特点:主、俯视图长对正;主、左视图高平齐;俯、左视图宽相等,前后对应.
2.画三视图时的注意事项:(1)主、俯视图长对正;主、左视图高平齐;俯、左视图宽相等,前后对应.(2)在三视图中,需要画出所有的轮廓线,其中,视线所见的轮廓
线画实线,看不见的轮廓线画虚线.③同一物体放置的位置不同,所画的三视图可能不同.
知识2
组合体
【问题导思】
日常生活中,我们遇到的几何体很多是组合体,如螺丝帽,矿泉水瓶等.(1)螺丝帽的俯视图是怎样的平面图形?(2)矿泉水瓶的主视图是怎样的平面图形?(3)组合体的三视图都完全不一样吗?
【提示】 (1)一个正六边形和中间一个圆.
(2)如图:
(3)不一定,例如矿泉水瓶的主视图和左视图一样.
1.定义:由基本几何体生成的几何体叫作组合体.
2.两种基本形式:一种是将基本几何体拼接成组合体;另一种是从基本几何体中切掉或挖掉部分构成组何体.
类型1
简单几何体的三视图
例1 画出如图1-3-1所示的几何体的三视图.
图1-3-1
【思路探究】 观察图形→确定方向→画三视图
【自主解答】 三视图如图所示:
规律方法
1.本题在画主视图与左视图时,易出现直接画成长方形的错误,导致这种错误的原因是对画三视图的规则理解不清.
2.在画三视图时,要想象几何体的后面、右面、下面各有一个屏幕,一组平行光线分别从前面、左面、上面垂直照射,我们画的是影子的轮廓,再验证几何体的轮廓线,看到的画实线,不能看到的画虚线.
互动探究
将本例中的正六棱柱换成如图1-3-2所示的正五棱柱呢?
图1-3-2
【解】 三视图如图所示:
类型2
简单组合体的三视图
例2 如图1-3-3所示的一实物,画出它的三视图.
图1-3-3
【思路探究】 观察图形→确定组成形式→画三视图
【自主解答】 如图所示的组合体可以看作是下图所示的几何体的组合.
三视图如图所示:
规律方法
1.画组合体的三视图时,对它们的交线位置一定要有足够的重视,如本题中的主视图.
2.在绘制简单组合体的三视图时,首先要分析组合体是由哪几部分组成,各部分是怎样的简单几何体,以及它们的相对位置;其次要注意实线、虚线的处理.
变式训练
画出如图1-3-4所示的几何体的三视图.
图1-3-4
【解】 三视图如图所示.
类型3
由三视图还原实物直观图
例3 如图1-3-5是某几何体的三视图,想象该几何体的结构特征,并画出该几何体的实物草图.
图1-3-5
【思路探究】 (1)哪些几何体的主视图是长方形?
(2)哪些几何体的左视图是长方形?
(3)哪些几何体的俯视图是圆?
【自主解答】 由于俯视图含有一个圆和一个四边形,则该几何体是由旋转体和多面体拼接而成的组合体,结合主视图和左视图可知,该几何体的上面是一个圆柱,下面是一个四棱柱.该几何体的实物草图如图所示.
规律方法
1.由三视图还原实物直观图的步骤
(1)看俯视图:判断几何体是多面体还是旋转体;确定几何体在前后左右方向所占空间;
(2)看主视图、左视图:联想常见几何体,从实虚线变化、几何体组成方式等角度判断结构特征;
(3)画直观图:由几何体的结构特征画出直观图.
2.看图和想图是两个重要的步骤,“想”寓于“看”中,形体分析的看图方法是解决此类问题的常用方法.
变式训练
根据如图1-3-6三视图想象该几何体的结构特征,并画出该几何体的实物草图.
图1-3-6
【解】 实物草图如下:
忽视三视图的规则致误
典例 画出如图1-3-7的物体的三视图.
图1-3-7
【错解】
【错因分析】 三视图出现多处错误.首先,主视图和左视图的高应该是相同的,而所画的视图没有做到这一点;其次,左视图的宽应该和俯视图的高一致,这一点也没有做到;再次,主视图的长与俯视图的长应对齐,这点还是没有做到;最后,图中有一条看不到的棱应该用虚线表示出来,所以答案存在多处错误.
【防范措施】 注意画三视图的规则,即这三者之间的等量关系,再注意虚、实线的区分.
【正解】 如图所示.
1.对于画几何体的三视图,要实虚线分清,可以解释为“眼见为实,不见为虚”.对于同一物体放置的位置不同,所画的三视图可能不同.
2.对于画简单组合体的三视图,要先弄清由哪几个基本几何体组合而成,并注意它们的组成方式,特别是它们的交线位置.
3.对于还原组合体,需要综合主视图、左视图、俯视图的特征,确定分界线,找出组成组合体的简单几何体,再将组合体还原,其中确定分界线是正确还原的关键.
1.下列各项不属于三视图的是( )
A.主视图 B.左视图
C.后视图
D.俯视图
【解析】 三视图指的是主视图、左视图、俯视图.故选C.
【答案】 C
2.图1-3-8所示的圆锥的左视图是( )
图1-3-8
【解析】 此圆锥的左视图为圆,顶点在圆心处,故C正确.
【答案】 C
3.图1-3-9中三视图所表示物体的形状为______.
图1-3-9
【解析】 图中三视图所表示物体的形状为圆柱.
【答案】 圆柱
4.画出如图1-3-10所示几何体的三视图.
图1-3-10
【解】
一、选择题
1.对于几何体的三视图,下列说法正确的是( )
A.主视图反映物体的长和高
B.俯视图反映物体的长和高
C.如果一个几何体的主视图和左视图都是等腰梯形,则这个几何体是圆台
D.如果一个几何体的三视图都为圆,则此几何体为圆柱
【解析】 三视图中的主视图,左视图,俯视图分别反映物体的长、高,宽、高,长、宽,因此A正确,B错误;C描述的几何体还可能为正四棱台;D选项描述的几何体是球.
【答案】 A
2.已知某空间几何体的三视图如图1-3-11所示,则此几何体为( )
图1-3-11
A.圆台 B.四棱锥
C.四棱柱
D.四棱台
【解析】 由主视图和左视图可以判断一定的棱台或圆台,又由俯视图可知一定为棱台且为四棱台.
【答案】 D
3.找出图1-3-12中三视图所对应的实物图形是( )
图1-3-12
【解析】 由三视图的作法易知实物图形应为C.
【答案】 C
图1-3-13
4.一个去掉一角的长方体的直观图如图1-3-13所示,关于它的三视图,下列画法正确的是( )
A.它的主视图是:
B.它的主视图是:
C.它的左视图是:
D.它的俯视图是:
【解析】 抓住几何体的结构特征,结合三视图的画法可知A正确,左视图框内应是一虚斜线,俯视图中的虚线应为实线.
【答案】 A
5.一个简单几何体的主视图、左视图如图1-3-14所示,则其俯视图不可能为:①长方形;②正方形;③圆;④椭圆.
图1-3-14
其中正确的是( )
A.①②
B.②③
C.③④
D.①④
【解析】 若俯视图为正方形或圆时,主视图和左视图中矩形的宽应该相等,故②③不可能.
【答案】 B
二、填空题
6.某物体的实物图如图(甲)所示,在其三视图中,图①是________;图②是________;图③是________.
图1-3-15
【解析】 根据三视图的特点知①是主视图,②是俯视图,③是左视图.
【答案】 主视图 俯视图 左视图
7.如图1-3-16所示的三视图代表的立体图形是________.
图1-3-16
【解析】 由三视图知此几何体为一个正六棱锥.
【答案】 正六棱锥
8.如图1-3-17所示是一个圆锥的三视图,则该圆锥的高为______cm.
图1-3-17
【解析】 由三视图知,圆锥的母线长为3
cm,底面圆的直径为3
cm,所以圆锥的轴截面也是边长为3
cm的等边三角形,所以圆锥的高为=(cm).
【答案】
三、解答题
9.给出下面一个几何体,根据要求画出它的三视图:
图1-3-18
【解】 该几何体的三视图形状如下:
10.某座楼由相同的若干个房间组成,该楼的三视图如图1-3-19.
图1-3-19
问:(1)该楼有几层?从前往后最多要走过几个房间?
(2)最高一层的房间在什么位置?该楼最多有几个房间?
【解】 (1)该楼共有3层,可以从主视图和左视图中看出;从前往后最多要走过3个房间,可以从俯视图中看出.
(2)最高一层的房间在左后方,可以从左视图中看出.楼的大致形状如图所示,最多有10个房间.
11.如图1-3-20是一个空间几何体的三视图,其中主视图和左视图都是边长为2的正三角形,俯视图是一个正方形.
图1-3-20
(1)在给定的直角坐标系中作出这个几何体的直观图(不写作法);
(2)求这个几何体的高.
【解】 (1)直观图如图.
(2)这个几何体是一个正四棱锥,它的底面边长为2,高在正视图(或左视图)中可求,高h=2sin
60°=.
备选例题
画出下列几何体的三视图(阴影面为主视面).
【思路探究】 有了主视面,根据三视图特点画出三视图.
【自主解答】 三视图如图.
规律方法
画组合体的三视图时,首先要确定主视、左视和俯视的方向,然后从三个方向观察组合体的轮廓线,还要搞清楚组合体是由哪几种基本几何体组成的,并注意各基本几何体的组成方式及组接位置,其组接的交线往往又是组合体的轮廓线,被挡住的要画成虚线.
备选变式
画出如图所示的组合体的三视图.(阴影部分为主视面,尺寸不作严格要求)
【解】 这个组合体的三视图如下:
