1.3 三视图 同步练习2(含答案)
文档属性
| 名称 | 1.3 三视图 同步练习2(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 318.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览


文档简介
1.3
三视图
同步练习
一、选择题(每小题4分,共16分)
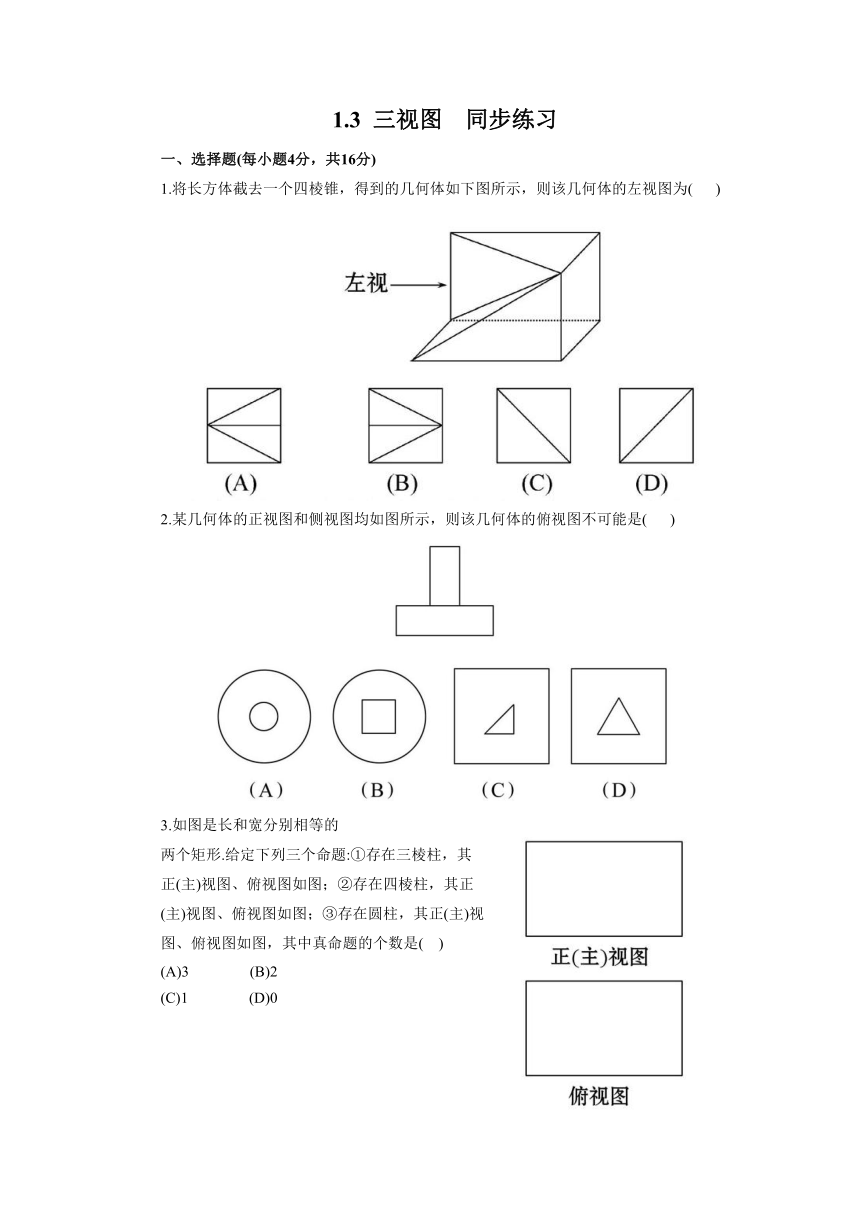
1.将长方体截去一个四棱锥,得到的几何体如下图所示,则该几何体的左视图为(
)
2.某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是(
)
3.如图是长和宽分别相等的
两个矩形.给定下列三个命题:①存在三棱柱,其
正(主)视图、俯视图如图;②存在四棱柱,其正
(主)视图、俯视图如图;③存在圆柱,其正(主)视
图、俯视图如图,其中真命题的个数是(
)
(A)3
(B)2
(C)1
(D)0
4.若某几何体的三视图如图所示,则这个几何体的直观图可以是(
)
二、填空题(每小题4分,共8分)
5.一个几何体的主视图为一个三角形,则这个几何体可能是下列几何体中的_________.(填入所有可能的几何体前的编号)
①三棱锥
②四棱锥
③三棱柱
④四棱柱
⑤圆锥
⑥圆柱
6.(易错题)一个正三棱柱的侧棱长和底面边
长均等于它的三视图中的俯视图如图所示,
左视图是一个矩形,则该矩形的面积为_________.
三、解答题(每小题8分,共16分)
7.画出下面物体的三视图.
8.下面是几何体的三视图,请画出该几何体的实物草图.
【挑战能力】
(10分)如图是由小立方块组成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,请画出它的主视图和左视图.
答案解析
1.【解析】选D.被截去的四棱锥的三条可见侧棱中,有两条为正方体的面对角线,它们在右侧面上的投影与右侧面(正方形)的两条边重合,另一条为正方体的体对角线,它在右侧面上的投影与右侧面的对角线重合,对照各图及对角线方向,D正确.
2.【解题指南】从俯视图观察可知,正视图和侧视图不同的是D,正视图应有虚线.
【解析】选D.由“正视图俯视图等长,侧视图俯视图等宽”,知该几何体正视图与侧视图相同,而D项中正视图与侧视图不同,可知选D.
3.【解析】选A.①可以是放倒的三棱柱,故①正确.存在正四棱柱,其三视图均为矩形,满足条件,故②正确.对于任意的圆柱,其三视图有两个为矩形,一个是以底面半径为半径的圆,满足条件,故③正确.故选A.
4.【解题指南】结合三视图利用排除法求解.
【解析】选B.由主视图可排除A,C,由左视图可判断该几何体的直观图是B.
5.【解析】三棱锥、四棱锥和圆锥的主视图都是三角形,当三棱柱的一个侧面平行于水平面、底面对着观测者时其主视图是三角形,四棱柱、圆柱无论怎样放置,其主视图都不可能是三角形.
答案:①②③⑤
6.【解析】由俯视图知该正三棱柱的直观图如图所示,
其中M,N分别是边AB,A1B1的中点,矩形MNC1C为左
视图.
∵△ABC为正三角形且M为边AB的中点,
∴
∴矩形MNC1C的面积为6×=,即左视图的面积为.
答案:
【误区警示】解答本题易把侧面AA1C1C当作该几何体的左视图而致错.
7.【解析】三视图如图所示:
【方法技巧】画三视图的诀窍
由三视图的作图原则可知:(1)主视图和俯视图共同反映了物体左右方向的尺寸;(2)主视图和左视图共同反映了物体上下方向的尺寸;(3)俯视图和左视图共同反映了物体前后方向的尺寸.因此画一个物体的三视图不仅要确定其形状,而且要确定三视图之间的线段大小关系.画三视图时一般遵循从下层向上层,从左边到右边的原则.
8.【解析】由三视图得实物草图如下图所示.
【挑战能力】
【解题指南】从俯视图可以看出,其主视图应该是3列,每列的立方块的个数分别是4,4,3;左视图应该是4列,每列的立方块的个数分别是3,3,4,3,由此可以想象该几何体的形状,得到其主视图和左视图.
【解析】该几何体的正视图和左视图如图:
三视图
同步练习
一、选择题(每小题4分,共16分)
1.将长方体截去一个四棱锥,得到的几何体如下图所示,则该几何体的左视图为(
)
2.某几何体的正视图和侧视图均如图所示,则该几何体的俯视图不可能是(
)
3.如图是长和宽分别相等的
两个矩形.给定下列三个命题:①存在三棱柱,其
正(主)视图、俯视图如图;②存在四棱柱,其正
(主)视图、俯视图如图;③存在圆柱,其正(主)视
图、俯视图如图,其中真命题的个数是(
)
(A)3
(B)2
(C)1
(D)0
4.若某几何体的三视图如图所示,则这个几何体的直观图可以是(
)
二、填空题(每小题4分,共8分)
5.一个几何体的主视图为一个三角形,则这个几何体可能是下列几何体中的_________.(填入所有可能的几何体前的编号)
①三棱锥
②四棱锥
③三棱柱
④四棱柱
⑤圆锥
⑥圆柱
6.(易错题)一个正三棱柱的侧棱长和底面边
长均等于它的三视图中的俯视图如图所示,
左视图是一个矩形,则该矩形的面积为_________.
三、解答题(每小题8分,共16分)
7.画出下面物体的三视图.
8.下面是几何体的三视图,请画出该几何体的实物草图.
【挑战能力】
(10分)如图是由小立方块组成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数,请画出它的主视图和左视图.
答案解析
1.【解析】选D.被截去的四棱锥的三条可见侧棱中,有两条为正方体的面对角线,它们在右侧面上的投影与右侧面(正方形)的两条边重合,另一条为正方体的体对角线,它在右侧面上的投影与右侧面的对角线重合,对照各图及对角线方向,D正确.
2.【解题指南】从俯视图观察可知,正视图和侧视图不同的是D,正视图应有虚线.
【解析】选D.由“正视图俯视图等长,侧视图俯视图等宽”,知该几何体正视图与侧视图相同,而D项中正视图与侧视图不同,可知选D.
3.【解析】选A.①可以是放倒的三棱柱,故①正确.存在正四棱柱,其三视图均为矩形,满足条件,故②正确.对于任意的圆柱,其三视图有两个为矩形,一个是以底面半径为半径的圆,满足条件,故③正确.故选A.
4.【解题指南】结合三视图利用排除法求解.
【解析】选B.由主视图可排除A,C,由左视图可判断该几何体的直观图是B.
5.【解析】三棱锥、四棱锥和圆锥的主视图都是三角形,当三棱柱的一个侧面平行于水平面、底面对着观测者时其主视图是三角形,四棱柱、圆柱无论怎样放置,其主视图都不可能是三角形.
答案:①②③⑤
6.【解析】由俯视图知该正三棱柱的直观图如图所示,
其中M,N分别是边AB,A1B1的中点,矩形MNC1C为左
视图.
∵△ABC为正三角形且M为边AB的中点,
∴
∴矩形MNC1C的面积为6×=,即左视图的面积为.
答案:
【误区警示】解答本题易把侧面AA1C1C当作该几何体的左视图而致错.
7.【解析】三视图如图所示:
【方法技巧】画三视图的诀窍
由三视图的作图原则可知:(1)主视图和俯视图共同反映了物体左右方向的尺寸;(2)主视图和左视图共同反映了物体上下方向的尺寸;(3)俯视图和左视图共同反映了物体前后方向的尺寸.因此画一个物体的三视图不仅要确定其形状,而且要确定三视图之间的线段大小关系.画三视图时一般遵循从下层向上层,从左边到右边的原则.
8.【解析】由三视图得实物草图如下图所示.
【挑战能力】
【解题指南】从俯视图可以看出,其主视图应该是3列,每列的立方块的个数分别是4,4,3;左视图应该是4列,每列的立方块的个数分别是3,3,4,3,由此可以想象该几何体的形状,得到其主视图和左视图.
【解析】该几何体的正视图和左视图如图:
