1.4 空间图形的基本关系与公理 同步练习1(含答案)
文档属性
| 名称 | 1.4 空间图形的基本关系与公理 同步练习1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 227.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览

文档简介
1.4
空间图形的基本关系与公理
同步练习
一、选择题(每小题4分,共16分)
1.在三棱锥P-ABC
的六条棱所在的直线中,异面直线共有(
)
(A)2对
(B)3对
(C)4对
(D)6对
2.已知空间四边形ABCD中,M,N分别为AB,CD的中点,则下列判断正确的是(
)
(A)MN≥(AC+BD)
(B)MN≤(AC+BD)
(C)MN=(AC+BD)
(D)MN<(AC+BD)
3.(易错题)在正方体ABCD
-A1B1C1D1各个表面的对角线中与AD1所成的角为
60°的有(
)
(A)4条
(B)6条
(C)8条
(D)10条
4.直三棱柱ABC—A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成的角等于(
)
(A)30°
(B)45°
(C)60°
(D)90°
二、填空题(每小题4分,共8分)
5.已知角α和角β的两边分别平行且一组边方向相同,另一组边的方向相反,若α=45°,则β=________.
6.在空间四边形ABCD中,点E,F,G,H分别为AB,BC,CD,DA的中点,若AC=BD,且AC⊥BD,则四边形EFGH的形状是________.
三、解答题(每小题8分,共16分)
7.如图所示,不共面的三条直线a,b,c交于点O,
在点O的同侧,在a,b,c上分别取点A和A1,B和B1,
C和C1,使得求证:△ABC∽△A1B1C1.
8.在正方体ABCD
-A1B1C1D1中,
求异面直线AC1与B1D1所成的角.
【挑战能力】
(10分)在长方体ABCD
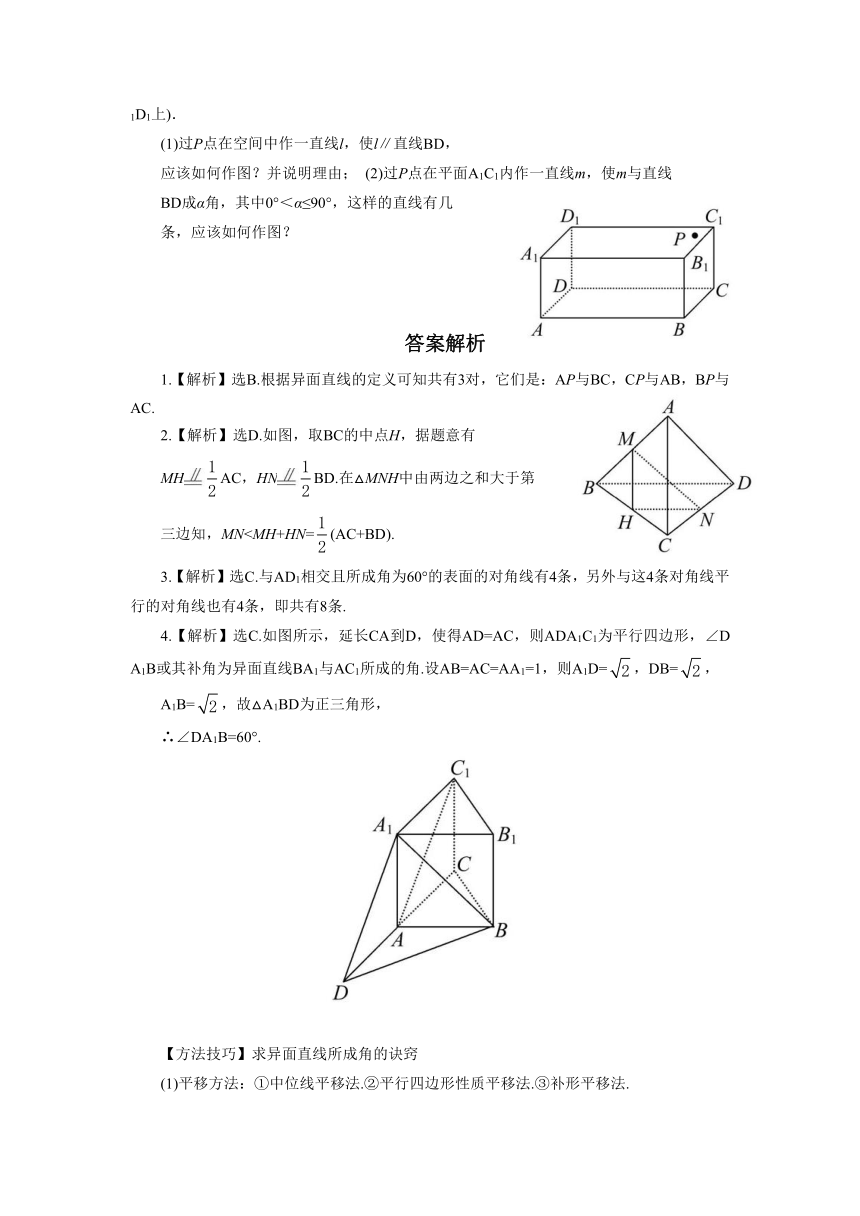
-A1B1C1D1的面A1C1上有一点P(如图所示,其中P点不在对角线B1D1上).
(1)过P点在空间中作一直线l,使l∥直线BD,
应该如何作图?并说明理由;
(2)过P点在平面A1C1内作一直线m,使m与直线
BD成α角,其中0°<α≤90°,这样的直线有几
条,应该如何作图?
答案解析
1.【解析】选B.根据异面直线的定义可知共有3对,它们是:AP与BC,CP与AB,BP与AC.
2.【解析】选D.如图,取BC的中点H,据题意有
MHAC,HNBD.在△MNH中由两边之和大于第
三边知,MN3.【解析】选C.与AD1相交且所成角为60°的表面的对角线有4条,另外与这4条对角线平行的对角线也有4条,即共有8条.
4.【解析】选C.如图所示,延长CA到D,使得AD=AC,则ADA1C1为平行四边形,∠DA1B或其补角为异面直线BA1与AC1所成的角.设AB=AC=AA1=1,则A1D=,DB=,
A1B=,故△A1BD为正三角形,
∴∠DA1B=60°.
【方法技巧】求异面直线所成角的诀窍
(1)平移方法:①中位线平移法.②平行四边形性质平移法.③补形平移法.
(2)平移直线是寻找两条异面直线所成角的过程,线的平移是在某个平面中进行的,该面的特点:①该平面包含其中一条异面直线,②该平面与另一条异面直线平行.
(3)求角或求角的三角函数值的一般步骤:①构造三角形,②解三角形求角或求角的三角函数值.
5.【解析】由等角定理,两角两组对边分别平行,一组方向相同,另一组方向相反,则两角互补,所以β=135°.
答案:135°
6.【解题指南】由中位线定理结合已知条件进行判断.
【解析】如图,E,F,G,H分别为中点,∴EFAC,
GHAC,∴EFGH,∴四边形EFGH为平行四边形.
又
AC⊥BD,∴FG⊥GH.∵AC=BD,
∴FG=GH,∴EFGH为正方形.
答案:正方形
7.【解题指南】由比例式先证明平行,结合等角定理说明对应角相等即可证明.
【证明】∵∴A1B1∥AB,
∵∴B1C1∥BC,
结合图形,由等角定理可得∠A1B1C1=∠ABC,
同理可证∠B1A1C1=∠BAC,∴△ABC∽△A1B1C1.
8.【解题指南】先作出异面直线AC1与B1D1所成的角,然后在三角形中求角.
【解析】如图,连接A1C1交B1D1于点O,则O为
A1C1的中点,取A1A的中点E,连接EO,EB1,则
EOAC1.所以∠EOB1为异面直线AC1与B1D1所成
的角或其补角.设该正方体棱长为2a,则在△B1OE
中,B1O=B1D1=,
EO=AC1=
因为EO2+B1O2=B1E2,所以△B1OE为直角三角形,且∠EOB1=90°,所以AC1与B1D1所成的角为90°.
【挑战能力】
【解析】(1)连接B1D1,在平面A1C1内过P点作直线l,
使l∥B1D1,则l即为所求作的直线.
∵B1D1∥BD,l∥B1D1,∴l∥直线BD.
(2)在平面A1C1内作直线m,
使直线m与B1D1相交成α角,
∵BD∥B1D1,∴直线m与直线BD也成α角,
即直线m为所求作的直线.
由图知m与BD是异面直线,
且m与BD所成的角α满足:0°<α≤90°.
当α=90°时,这样的直线m有且只有一条,
当α≠90°时,这样的直线m有两条.
空间图形的基本关系与公理
同步练习
一、选择题(每小题4分,共16分)
1.在三棱锥P-ABC
的六条棱所在的直线中,异面直线共有(
)
(A)2对
(B)3对
(C)4对
(D)6对
2.已知空间四边形ABCD中,M,N分别为AB,CD的中点,则下列判断正确的是(
)
(A)MN≥(AC+BD)
(B)MN≤(AC+BD)
(C)MN=(AC+BD)
(D)MN<(AC+BD)
3.(易错题)在正方体ABCD
-A1B1C1D1各个表面的对角线中与AD1所成的角为
60°的有(
)
(A)4条
(B)6条
(C)8条
(D)10条
4.直三棱柱ABC—A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成的角等于(
)
(A)30°
(B)45°
(C)60°
(D)90°
二、填空题(每小题4分,共8分)
5.已知角α和角β的两边分别平行且一组边方向相同,另一组边的方向相反,若α=45°,则β=________.
6.在空间四边形ABCD中,点E,F,G,H分别为AB,BC,CD,DA的中点,若AC=BD,且AC⊥BD,则四边形EFGH的形状是________.
三、解答题(每小题8分,共16分)
7.如图所示,不共面的三条直线a,b,c交于点O,
在点O的同侧,在a,b,c上分别取点A和A1,B和B1,
C和C1,使得求证:△ABC∽△A1B1C1.
8.在正方体ABCD
-A1B1C1D1中,
求异面直线AC1与B1D1所成的角.
【挑战能力】
(10分)在长方体ABCD
-A1B1C1D1的面A1C1上有一点P(如图所示,其中P点不在对角线B1D1上).
(1)过P点在空间中作一直线l,使l∥直线BD,
应该如何作图?并说明理由;
(2)过P点在平面A1C1内作一直线m,使m与直线
BD成α角,其中0°<α≤90°,这样的直线有几
条,应该如何作图?
答案解析
1.【解析】选B.根据异面直线的定义可知共有3对,它们是:AP与BC,CP与AB,BP与AC.
2.【解析】选D.如图,取BC的中点H,据题意有
MHAC,HNBD.在△MNH中由两边之和大于第
三边知,MN
4.【解析】选C.如图所示,延长CA到D,使得AD=AC,则ADA1C1为平行四边形,∠DA1B或其补角为异面直线BA1与AC1所成的角.设AB=AC=AA1=1,则A1D=,DB=,
A1B=,故△A1BD为正三角形,
∴∠DA1B=60°.
【方法技巧】求异面直线所成角的诀窍
(1)平移方法:①中位线平移法.②平行四边形性质平移法.③补形平移法.
(2)平移直线是寻找两条异面直线所成角的过程,线的平移是在某个平面中进行的,该面的特点:①该平面包含其中一条异面直线,②该平面与另一条异面直线平行.
(3)求角或求角的三角函数值的一般步骤:①构造三角形,②解三角形求角或求角的三角函数值.
5.【解析】由等角定理,两角两组对边分别平行,一组方向相同,另一组方向相反,则两角互补,所以β=135°.
答案:135°
6.【解题指南】由中位线定理结合已知条件进行判断.
【解析】如图,E,F,G,H分别为中点,∴EFAC,
GHAC,∴EFGH,∴四边形EFGH为平行四边形.
又
AC⊥BD,∴FG⊥GH.∵AC=BD,
∴FG=GH,∴EFGH为正方形.
答案:正方形
7.【解题指南】由比例式先证明平行,结合等角定理说明对应角相等即可证明.
【证明】∵∴A1B1∥AB,
∵∴B1C1∥BC,
结合图形,由等角定理可得∠A1B1C1=∠ABC,
同理可证∠B1A1C1=∠BAC,∴△ABC∽△A1B1C1.
8.【解题指南】先作出异面直线AC1与B1D1所成的角,然后在三角形中求角.
【解析】如图,连接A1C1交B1D1于点O,则O为
A1C1的中点,取A1A的中点E,连接EO,EB1,则
EOAC1.所以∠EOB1为异面直线AC1与B1D1所成
的角或其补角.设该正方体棱长为2a,则在△B1OE
中,B1O=B1D1=,
EO=AC1=
因为EO2+B1O2=B1E2,所以△B1OE为直角三角形,且∠EOB1=90°,所以AC1与B1D1所成的角为90°.
【挑战能力】
【解析】(1)连接B1D1,在平面A1C1内过P点作直线l,
使l∥B1D1,则l即为所求作的直线.
∵B1D1∥BD,l∥B1D1,∴l∥直线BD.
(2)在平面A1C1内作直线m,
使直线m与B1D1相交成α角,
∵BD∥B1D1,∴直线m与直线BD也成α角,
即直线m为所求作的直线.
由图知m与BD是异面直线,
且m与BD所成的角α满足:0°<α≤90°.
当α=90°时,这样的直线m有且只有一条,
当α≠90°时,这样的直线m有两条.
