1.4 空间图形的基本关系与公理 同步练习2(含答案)
文档属性
| 名称 | 1.4 空间图形的基本关系与公理 同步练习2(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览

文档简介
1.4
空间图形的基本关系与公理
同步练习
1.下列叙述中错误的是( ).
A.若P∈α,P∈β且α∩β=l,则P∈l
B.三点A,B,C只能确定一个平面
C.若直线a∩b=A,则直线a与b能够确定一个平面
D.若A∈l,B∈l且A∈α,B∈α,则lα
2.下列说法正确的个数有( ).
(1)三角形、梯形一定是平面图形;
(2)若四边形的两条对角线相交于一点,则该四边形是平面图形;
(3)三条平行线最多可确定三个平面;
(4)平面α和β相交,它们只有有限个公共点;
(5)若A,B,C,D四个点既在平面α内,又在平面β内,则这两平面重合.
A.2
B.3
C.4
D.5
3.在空间四边形ABCD的边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF与HG交于点M,则( ).
A.M一定在直线AC上
B.M一定在直线BD上
C.M可能在直线AC上,也可能在BD上
D.M不在AC上,也不在BD上
4.如图,平面α∩平面β=l,点A∈α,点B∈α,且点C∈β,点Cl.又AB∩l=R,设A,B,C三点确定的平面为γ,则β∩γ是( ).
A.直线AC
B.直线BC
C.直线CR
D.以上均错
5.平行六面体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( ).
A.3
B.4
C.5
D.6
6.若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成( ).
A.5部分
B.6部分
C.7部分
D.8部分
7.四条线段顺次首尾相接,最多可以确定平面的个数是__________.
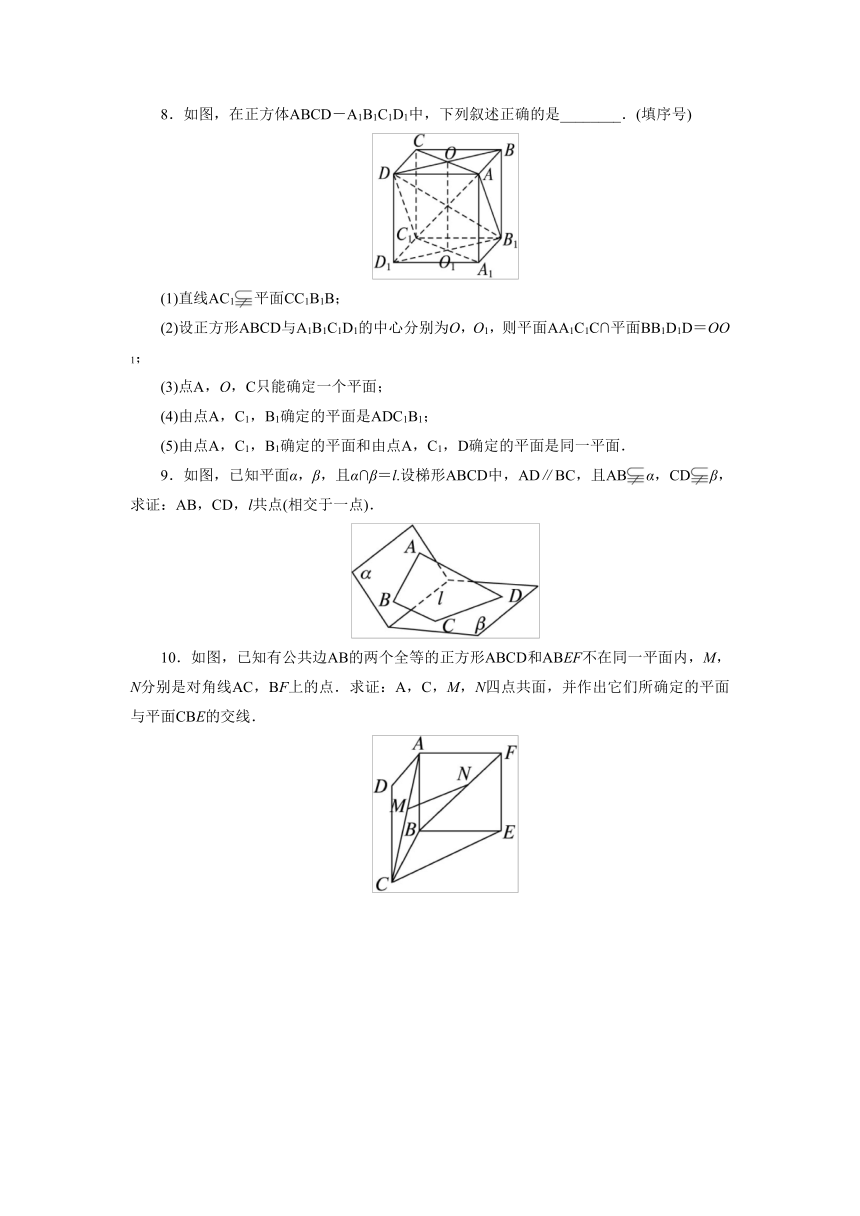
8.如图,在正方体ABCD-A1B1C1D1中,下列叙述正确的是________.(填序号)
(1)直线AC1平面CC1B1B;
(2)设正方形ABCD与A1B1C1D1的中心分别为O,O1,则平面AA1C1C∩平面BB1D1D=OO1;
(3)点A,O,C只能确定一个平面;
(4)由点A,C1,B1确定的平面是ADC1B1;
(5)由点A,C1,B1确定的平面和由点A,C1,D确定的平面是同一平面.
9.如图,已知平面α,β,且α∩β=l.设梯形ABCD中,AD∥BC,且ABα,CDβ,求证:AB,CD,l共点(相交于一点).
10.如图,已知有公共边AB的两个全等的正方形ABCD和ABEF不在同一平面内,M,N分别是对角线AC,BF上的点.求证:A,C,M,N四点共面,并作出它们所确定的平面与平面CBE的交线.
参考答案
1答案:B
2答案:B 解析:只有(1)(2)(3)正确.两平面相交有无数个交点,所以(4)错;对于(5),若四个点共线,则过四点有无数个平面,所以平面α与平面β就不一定重合.
3答案:A 解析:因为E,F,G,H是空间四边形ABCD的边AB,
BC,CD,DA上的四点,EF与HG交于点M,所以M为平面ABC与平面ACD的公共点.而两个平面的交线为AC,所以M一定在直线AC上,故选A.
4答案:C 解析:∵C∈平面ABC,AB平面ABC,而R∈AB,
∴R∈平面ABC.而C∈β,lβ,R∈l,∴R∈β,
∴点C,点R为两平面ABC与β的公共点,∴β∩γ=CR.
5答案:C 解析:如图,与AB共面也与CC1共面的棱有CD,BC,BB1,AA1,C1D1,共5条.
6答案:C 解析:如三棱柱的三个侧面,将其延伸可知将空间分为了7部分.
7答案:4 解析:与不共面的四点可确定的平面个数相同.不妨设四个点为A,B,C,D,则由A,B,C确定一个平面.A,B,D;B,C,D;A,C,D分别可确定一个平面,共计4个.
8答案:(2)(4)(5)
9答案:证明:∵梯形ABCD中,AD∥BC,
∴AB,CD是梯形ABCD的两腰,
∴AB,CD必相交于一点.设AB∩CD=M,
又ABα,CDβ,
∴M∈α,
M∈β,
∴M在α与β的交线上.
又∵α∩β=l,
∴M∈l,
即AB,CD,l共点.
10答案:解:连接AN,CN.由题意可知AC∩AN=A,∴直线AC与直线AN确定平面ACN.又M∈AC,∴M∈平面ACN,即A,C,M,N四点共面,该平面即为平面ACN.
要确定两个平面的交线,可以先确定交线上的两个点,然后连接即可得到.延长AN交BE的延长线于点G.
∵G∈BE,BE平面CBE,
∴G∈平面CBE.
又G∈AN,AN平面ACN,
∴G∈平面ACN,
即G为平面ACN和平面CBE的公共点.又C∈平面CBE,C∈平面ACN,∴CG为两个平面的交线.
空间图形的基本关系与公理
同步练习
1.下列叙述中错误的是( ).
A.若P∈α,P∈β且α∩β=l,则P∈l
B.三点A,B,C只能确定一个平面
C.若直线a∩b=A,则直线a与b能够确定一个平面
D.若A∈l,B∈l且A∈α,B∈α,则lα
2.下列说法正确的个数有( ).
(1)三角形、梯形一定是平面图形;
(2)若四边形的两条对角线相交于一点,则该四边形是平面图形;
(3)三条平行线最多可确定三个平面;
(4)平面α和β相交,它们只有有限个公共点;
(5)若A,B,C,D四个点既在平面α内,又在平面β内,则这两平面重合.
A.2
B.3
C.4
D.5
3.在空间四边形ABCD的边AB,BC,CD,DA上分别取E,F,G,H四点,如果EF与HG交于点M,则( ).
A.M一定在直线AC上
B.M一定在直线BD上
C.M可能在直线AC上,也可能在BD上
D.M不在AC上,也不在BD上
4.如图,平面α∩平面β=l,点A∈α,点B∈α,且点C∈β,点Cl.又AB∩l=R,设A,B,C三点确定的平面为γ,则β∩γ是( ).
A.直线AC
B.直线BC
C.直线CR
D.以上均错
5.平行六面体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( ).
A.3
B.4
C.5
D.6
6.若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成( ).
A.5部分
B.6部分
C.7部分
D.8部分
7.四条线段顺次首尾相接,最多可以确定平面的个数是__________.
8.如图,在正方体ABCD-A1B1C1D1中,下列叙述正确的是________.(填序号)
(1)直线AC1平面CC1B1B;
(2)设正方形ABCD与A1B1C1D1的中心分别为O,O1,则平面AA1C1C∩平面BB1D1D=OO1;
(3)点A,O,C只能确定一个平面;
(4)由点A,C1,B1确定的平面是ADC1B1;
(5)由点A,C1,B1确定的平面和由点A,C1,D确定的平面是同一平面.
9.如图,已知平面α,β,且α∩β=l.设梯形ABCD中,AD∥BC,且ABα,CDβ,求证:AB,CD,l共点(相交于一点).
10.如图,已知有公共边AB的两个全等的正方形ABCD和ABEF不在同一平面内,M,N分别是对角线AC,BF上的点.求证:A,C,M,N四点共面,并作出它们所确定的平面与平面CBE的交线.
参考答案
1答案:B
2答案:B 解析:只有(1)(2)(3)正确.两平面相交有无数个交点,所以(4)错;对于(5),若四个点共线,则过四点有无数个平面,所以平面α与平面β就不一定重合.
3答案:A 解析:因为E,F,G,H是空间四边形ABCD的边AB,
BC,CD,DA上的四点,EF与HG交于点M,所以M为平面ABC与平面ACD的公共点.而两个平面的交线为AC,所以M一定在直线AC上,故选A.
4答案:C 解析:∵C∈平面ABC,AB平面ABC,而R∈AB,
∴R∈平面ABC.而C∈β,lβ,R∈l,∴R∈β,
∴点C,点R为两平面ABC与β的公共点,∴β∩γ=CR.
5答案:C 解析:如图,与AB共面也与CC1共面的棱有CD,BC,BB1,AA1,C1D1,共5条.
6答案:C 解析:如三棱柱的三个侧面,将其延伸可知将空间分为了7部分.
7答案:4 解析:与不共面的四点可确定的平面个数相同.不妨设四个点为A,B,C,D,则由A,B,C确定一个平面.A,B,D;B,C,D;A,C,D分别可确定一个平面,共计4个.
8答案:(2)(4)(5)
9答案:证明:∵梯形ABCD中,AD∥BC,
∴AB,CD是梯形ABCD的两腰,
∴AB,CD必相交于一点.设AB∩CD=M,
又ABα,CDβ,
∴M∈α,
M∈β,
∴M在α与β的交线上.
又∵α∩β=l,
∴M∈l,
即AB,CD,l共点.
10答案:解:连接AN,CN.由题意可知AC∩AN=A,∴直线AC与直线AN确定平面ACN.又M∈AC,∴M∈平面ACN,即A,C,M,N四点共面,该平面即为平面ACN.
要确定两个平面的交线,可以先确定交线上的两个点,然后连接即可得到.延长AN交BE的延长线于点G.
∵G∈BE,BE平面CBE,
∴G∈平面CBE.
又G∈AN,AN平面ACN,
∴G∈平面ACN,
即G为平面ACN和平面CBE的公共点.又C∈平面CBE,C∈平面ACN,∴CG为两个平面的交线.
