1.5 平行关系 教案
图片预览



文档简介
1.5
平行关系
教案
●三维目标
1.知识与技能
(1)理解直线与平面平行、平面与平面平行的判定定理的含义.(2)会判断线面、面面平行.
2.过程与方法
通过观察图形,借助已有知识,掌握线面、面面平行的判定定理,培养学生观察发现的能力和空间想象能力.
3.情感、态度与价值观
(1)让学生在发现中学习,增强学习的积极性.
(2)让学生了解空间与平面互相转换的数学思想.
●重点难点
重点:线面、面面平行的判定定理.
难点:利用平行的判定定理证明平行关系.
●教学建议
讲解平行关系时,教师可以从身边的实物为例引导学生去认识平行关系的判定,如观察书的边缘与书面的位置等,让学生在情景中学会感知,得出结论,教学中,可以让学生观察具体的长方体实物模型,以增强对判定定理的直观感知.
●教学流程
创设问题情境,引出两个问题:直线与平面、平面与平面的关系 引导学生通过观察回答问题,引出直线与平面平行、平面与平面平行的判定定理 通过例1及互动探究,使学生掌握直线平面平行的证明问题 通过例2及变式训练,使学生掌握,平面与平面平行的证明问题 通过例3及变式训练,使学生掌握,直线平面、平面平面平行的综合问题 归纳整合本节知识,作课堂小结 让学生完成当堂双基达标,巩固所学知识,反馈并矫正
课标解读
1.理解直线与平面平行、平面与平面平行的判定定理的含义,会判断线面、面面平行(重点).2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的判定定理,并知道其地位和作用(难点).
知识1
直线和平面平行的判定定理
【问题导思】
教室的门通过门轴可以自由的开关,在开关的过程中,门上竖直的一边与门轴所在边什么关系?与门轴所在墙面又是什么关系?
【提示】 门上竖直的一边与门轴所在边平行,与墙面也平行.
知识2
平面与平面平行的判定定理
【问题导思】
三角板的一边所在直线与桌面平行,这个三角板所在平面与桌面平行吗?三角板的两条边所在直线分别与桌面平行,情况又如何呢?
【提示】 三角板的一条边所在直线与桌面平行时,三角板所在平面与桌面可能平行,也可能相交.三角板的两条边所在直线分别与桌面平行时,三角板所在平面与桌面平行.
类型1
线面平行的判定
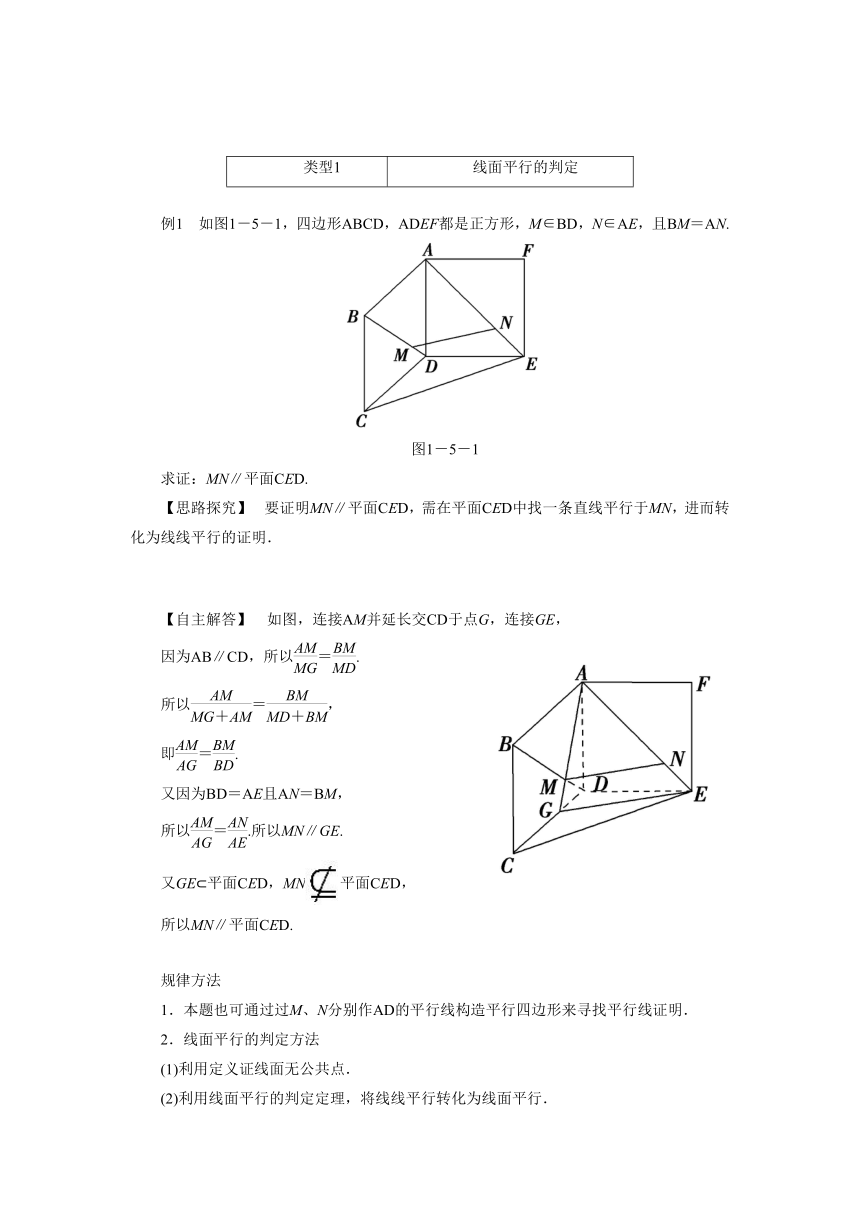
例1 如图1-5-1,四边形ABCD,ADEF都是正方形,M∈BD,N∈AE,且BM=AN.
图1-5-1
求证:MN∥平面CED.
【思路探究】 要证明MN∥平面CED,需在平面CED中找一条直线平行于MN,进而转化为线线平行的证明.
【自主解答】 如图,连接AM并延长交CD于点G,连接GE,
因为AB∥CD,所以=.
所以=,
即=.
又因为BD=AE且AN=BM,
所以=.所以MN∥GE.
又GE 平面CED,MN平面CED,
所以MN∥平面CED.
规律方法
1.本题也可通过过M、N分别作AD的平行线构造平行四边形来寻找平行线证明.
2.线面平行的判定方法
(1)利用定义证线面无公共点.
(2)利用线面平行的判定定理,将线线平行转化为线面平行.
互动探究
本例条件不变,求证:BF∥平面CDE.
【证明】 ∵四边形ABCD,ADEF都是正方形,
∴BC平行并等于AD平行并等于EF,∴BC平行并等于EF.
∴四边形BCEF是平行四边形,∴BF∥CE.
∵BF平面CDE,CE 平面CDE,∴BF∥平面CDE.
类型2
面面平行的判定
例2 已知四棱锥P—ABCD中,底面ABCD为平行四边形.点M、N、Q分别在PA、BD、PD上,且PM∶MA=BN∶ND=PQ∶QD.
图1-5-2
求证:平面MNQ∥平面PBC.
【思路探究】 (1)你认为证明线面平行、面面平行关键是什么?
(2)题中所给成比例线段有什么用?
(3)能否找到两条相交直线都和平面PBC平行?
【自主解答】 ∵PM∶MA=BN∶ND=PQ∶QD,
∴MQ∥AD,NQ∥BP.
∵BP 平面PBC,NQ平面PBC,
∴NQ∥平面PBC.
又底面ABCD为平行四边形,
∴BC∥AD,
∴MQ∥BC.
∵BC 平面PBC,MQ平面PBC,
∴MQ∥平面PBC.
又MQ∩NQ=Q,根据平面与平面平行的判定定理,得平面MNQ∥平面PBC.
规律方法
1.利用比例线段推出平行关系是解答本题的关键.
2.面面平行的判定方法
(1)利用定义,证面面无公共点.
(2)利用面面平行的判定定理转化为证明线面平行,即证明一个平面内的两条相交直线平行于另一个平面.
变式训练
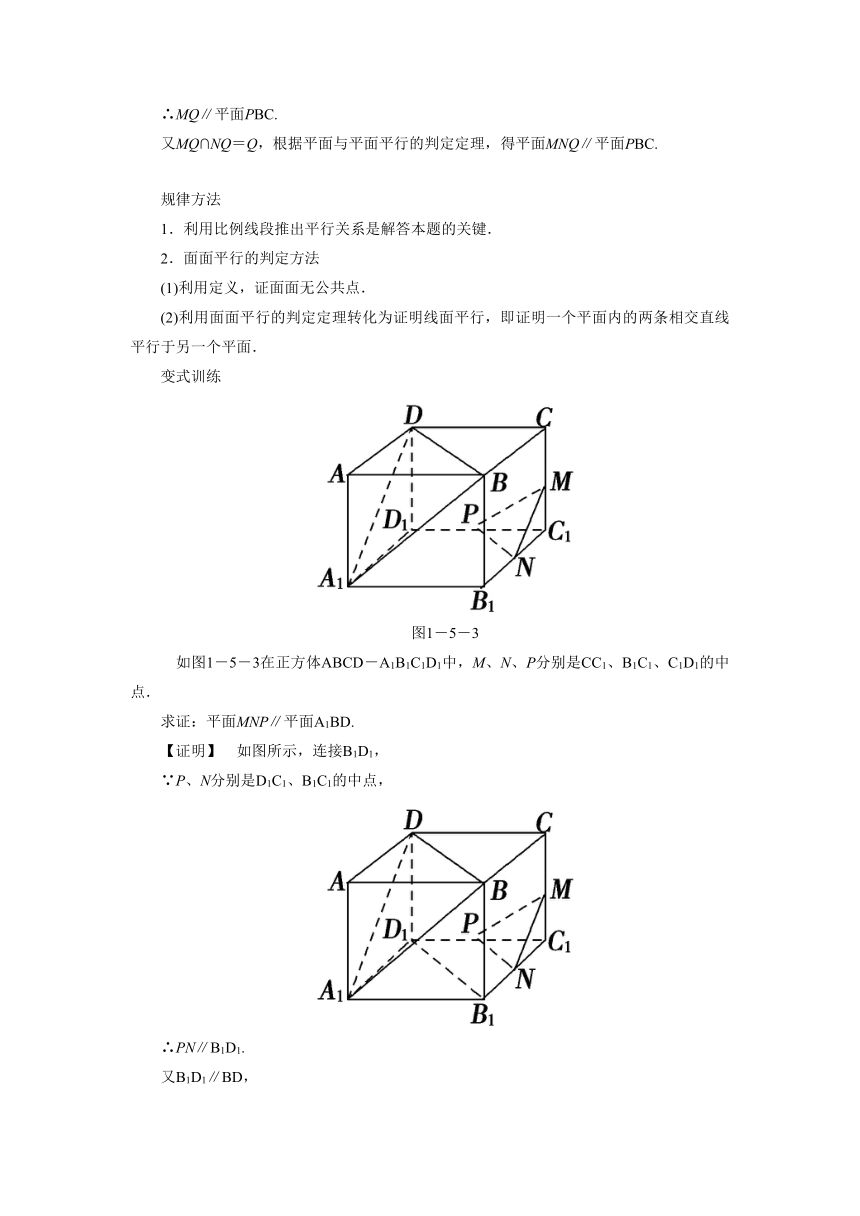
图1-5-3
如图1-5-3在正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、B1C1、C1D1的中点.
求证:平面MNP∥平面A1BD.
【证明】 如图所示,连接B1D1,
∵P、N分别是D1C1、B1C1的中点,
∴PN∥B1D1.
又B1D1∥BD,
∴PN∥BD,又PN平面A1BD,
BD 平面A1BD,
∴PN∥平面A1BD,
同理可得MN∥平面A1BD,
又∵MN∩PN=N,∴平面PMN∥平面A1BD.
类型3
平行关系的综合应用
例3 如图1-5-4,在正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,
图1-5-4
问:当点Q在什么位置时,平面D1BQ∥平面PAO?
【思路探究】 (1)由条件“P是DD1中点”,你猜想Q应在CC1的什么位置?
(2)PO与BD1平行吗?
【自主解答】 Q为CC1的中点时,平面D1BQ∥平面PAO.证明如下:
设Q为CC1中点,
则PD平行并等于QC,连接PQ,则由PQ平行并等于DC平行并等于AB,
可知四边形ABQP是平行四边形,
∴AP∥BQ.
∵AP平面D1BQ,BQ 平面D1BQ,
∴AP∥平面D1BQ.
∵O、P分别为BD、DD1的中点,∴OP∥BD1.
又OP
平面D1BQ,BD1 平面D1BQ,
∴OP∥平面D1BQ.
又AP∩PO=P,∴平面D1BQ∥平面PAO,
∴当点Q为CC1的中点时,平面D1BQ∥平面PAO.
规律方法
1.本题中由条件P是DD1中点猜想到Q应是CC1的中点是解题的关键.
2.对于条件缺失的探索性问题,解答过程中要明确目的,结合题目本身的特点与相应的定理大胆地猜想,然后加以证明.特别要注意中点、顶点等特殊点.
变式训练
如图1-5-5,正三棱柱ABC—A1B1C1的底面边长为2,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的点,EC=2FB=2.则当点M在什么位置时,MB∥平面AEF?试给出证明.
图1-5-5
【解】 当M为AC中点时,
MB∥平面AEF.
证明 如图,当M为AC中点时,过M作MG∥CE,交AE于G,连接GF.
∵M为AC中点,
∴MG平行并等于CE.
又FB∥CE,EC=2FB,
∴MG平行并等于FB.
∴四边形BFGM为平行四边形,
∴GF∥MB.
又GF 平面AEF,MB平面AEF,所以MB∥平面AEF.
忽视判定定理中的条件致误
典例 如图1-5-6,在正方体ABCD—A1B1C1D1中,M∈AD1,N∈BD,且D1M=DN,求证:MN∥平面CC1D1D.
【错解】 连AN并延长交DC于E,连接D1E
∵AB∥CD,
∴= =,
∵BD=AD1,D1M=DN,
∴=,∴MN∥D1E,
∴MN∥平面CC1D1D.
【错因分析】 忽视了直线与平面平行的判定定理中“lα,b α”这一条件,致使定理不完整.
【防范措施】 判定定理中的各个条件都不能忽视不能遗漏.
【正解】 连AN并延长交DC于E.连接D1E.
∵AB∥CD,
∴= =.
∵BD=AD1,
且D1M=DN,
∴=.
在△AD1E中,MN∥D1E,
又MN平面CC1D1D,D1E 平面CC1D1D,
∴MN∥平面CC1D1D.
1.直线与平面平行的关键是在已知平面内找一条直线和已知直线平行,即要证直线与平面平行,先证直线与直线平行.即由立体向平面转化,由高维向低维转化.
2.证明面面平行时,要按“线线平行”、“线面平行”、“面面平行”的证明顺序进行.当题目中有多个平面平行时,要注意平行平面的传递性.两平面平行的判定定理的条件中直线相交很重要,而且在解题中常常被忽视.
1.能保证直线a与平面α平行的条件是( )
A.aα,b α,a∥b
B.b α,a∥b
C.b α,c α,a∥c,且a∥b
D.b α,A∈a,B∈a,C∈b,D∈b,且AC=BD
【解析】 B、C、D均可能有a在平面α内.
【答案】 A
2.直线l,m,平面α、β,l α,m α,l∥β,m∥β,则α与β的位置关系是( )
A.平行
B.相交
C.异面
D.不确定
【解析】 α与β可能相交,也可能平行.
【答案】 D
3.已知两条相交直线a,b,且a∥平面α,则b与α的位置关系是________.
【解析】 由图可知,b与α平行或相交.
【答案】 平行或相交
图1-5-7
4.四棱锥P—ABCD中,AB=AD,∠BAD=60°,CD⊥AD,F,E分别是PA,AD的中点,求证:
平面PCD∥平面FEB.
【证明】 连接BD,在△ABD中,∠BAD=60°,AB=AD,
∴△ABD是等边三角形,E为AD的中点,
∴BE⊥AD.
又CD⊥AD,
∴在四边形ABCD中,BE∥CD.
又CD平面FEB,
BE 平面FEB,
∴CD∥平面FEB.
在△APD中,EF∥PD,
同理可得PD∥平面FEB.
又CD∩PD=D,
∴平面PCD∥平面FEB.
一、选择题
1.下列说法正确的是( )
A.平行于同一个平面的两条直线平行
B.同时与两异面直线平行的平面有无数多个
C.如果一条直线上有两点在一个平面外,则这条直线与这个平面平行
D.直线l不在平面α内,则l∥α
【解析】 A选项,若两直线相交且同时与此平面平行也是可以的;B选项,我们将异面直线都平移到空间中的某一点相交,则它们确定一个平面,与此平面平行的平面平行于这两条异面直线,显然这样的平面有无穷多个;C、D选项,若直线与平面相交,则直线有两点在平面外,直线也不在平面内,但l与α不平行.
【答案】 B
2.若M,N分别是△ABC边AB,AC的中点,MN与过直线BC的平面β的位置关系是( )
A.MN∥β
B.MN与β相交或MN β
C.MN∥β或MN β
D.MN∥β或MN与β相交或MN β
【解析】 当平面β与平面ABC重合时,有MN β;当平面β与平面ABC不重合时,则β∩平面ABC=BC.
∵M,N分别为AB,AC的中点,∴MN∥BC.
又MN
β,BC β,∴MN∥β.综上有MN∥β或MN β.
【答案】 C
3.如果AB、BC、CD是不在同一平面内的三条线段,则经过它们中点的平面和直线AC的位置关系是( )
A.平行 B.相交
C.AC在此平面内
D.平行或相交
【解析】 如图:E、F、G分别为AB、BC、CD的中点.
∵E、F分别是AB,BC的中点,
∴EF∥AC.
又EF 平面EFG,且AC
平面EFG.
∴AC∥平面EFG.
【答案】 A
4.在正方体ABCD-A1B1C1D1中,下列四对截面中彼此平行的一对截面是( )
A.平面A1BC1和平面ACD1
B.平面BDC1和平面B1D1C
C.平面B1D1D和平面BDA1
D.平面ADC1和平面AD1C
【解析】 如图,在截面A1BC1和截面AD1C中,
平面A1BC1∥平面ACD1.
【答案】 A
图1-5-8
5.如图1-5-8,在空间四边形ABCD中,E、F分别为边AB、AD上的点,且AE∶EB=AF∶FD=1∶4,又H、G分别为BC、CD的中点,则( )
A.BD∥平面EFGH,且四边形EFGH是矩形
B.EF∥平面BCD,且四边形EFGH是梯形
C.HG∥平面ABD,且四边形EFGH是菱形
D.EH∥平面ADC,且四边形EFGH是梯形
【解析】 ∵AE∶EB=AF∶FD=1∶4,
∴EF∥BD且EF=BD.
又H、G分别为BC、CD的中点,
∴HG平行并等于BD.
∴EF∥HG且EF≠HG.
∴四边形EFGH为梯形.
∵BD 平面BCD且EF
平面BCD.
∴EF∥平面BCD.
【答案】 B
二、填空题
图1-5-9
6.如图1-5-9所示,在空间四边形ABCD中,M∈AB,N∈AD,若=,则MN与平面BDC的位置关系是________.
【解析】 ∵=,∴MN∥BD.
又∵MN
平面BDC,BD 平面BDC,
∴MN∥平面BDC.
【答案】 平行
7.已知a、b、c为三条不重合的直线,α,β,γ为三个不重合平面,下面三个命题:
①a∥c,b∥c a∥b;②γ∥α,β∥α γ∥β;③a∥γ,α∥γ a∥α.
其中正确命题的序号是________.
【解析】 由平行公理,知①正确;由平面平行的传递性知②正确;③不正确,因为a可能在α内.
【答案】 ①②
8.在空间四边形PABC中,A1、B1、C1分别是△PBC、△PCA、△PAB的重心,则平面ABC与平面A1B1C1的位置关系是________.
【解析】 如图,连接PC1,PA1,并延长分别交AB,BC于E、F两点,由于C1、A1分别为重心.
∴E、F分别为AB、BC的中点,连接EF.
又∵==2.
∴A1C1∥EF.
又∵EF为△ABC边AC上的中位线,
∴EF∥AC,∴AC∥A1C1,
又A1C1 平面ABC,AC?平面ABC,
∴A1C1∥平面ABC,
同理A1B1∥平面ABC,
A1B1∩A1C1=A1,
∴平面A1B1C1∥平面ABC.
【答案】 平行
三、解答题
9.在三棱柱ABC—A′B′C′中,点E,D分别是B′C′与BC的中点.求证:平面A′EB∥平面ADC′.
【证明】 连接DE,
∵E,D分别是B′C′与BC的中点,
∴DE平行并等于AA′,
∴AA′ED是平行四边形,∴A′E∥AD.
∵A′E
平面ADC′,AD 平面ADC′.
∴A′E∥平面ADC′.
又BE∥DC′,BE
平面ADC′,DC′ 平面ADC′,
∴BE∥平面ADC′,
∵A′E 平面A′EB,BE 平面A′EB,
A′E∩BE=E,
∴平面A′EB∥平面ADC′.
图1-5-10
10.如图1-5-10,在直四棱柱ABCD-A1B1C1D1中,底面是梯形,AB∥CD,CD=2AB,P、Q分别是CC1、C1D1的中点,求证:面AD1C∥面BPQ.
【证明】 ∵D1Q=DC,AB平行并等于CD,∴D1Q
平行并等于AB.
∴四边形D1QBA为平行四边形,∴D1A平行并等于QB.
∵Q、P分别为D1C1、C1C的中点,∴QP∥D1C.
∵D1C∩D1A=D1,PQ∩QB=Q.
∴面AD1C∥面BPQ.
图1-5-11
11.如图1-5-11,E,F,G,H分别是正方体ABCD—A1B1C1D1的棱BC,CC1,C1D1,AA1的中点,求证:
(1)GE∥平面BB1D1D;
(2)平面BDF∥平面B1D1H.
【证明】 (1)取B1D1中点O,连接GO,OB,易证OG∥B1C1,
且OG=B1C1,BE∥B1C1,
且BE=B1C1,
∴OG∥BE且OG=BE,四边形BEGO为平行四边形,
∴OB∥GE.
∵OB
平面BDD1B1,
GE
平面BDD1B1,
∴GE∥平面BDD1B1.
(2)由正方体性质得
B1D1∥BD,
∵B1D1 平面BDF,BD 平面BDF,
∴B1D1∥平面BDF,连接HB,D1F,
易证HBFD1是平行四边形,得HD1∥BF.
∵HD1
平面BDF,BF 平面BDF,
∴HD1∥平面BDF,
∵B1D1∩HD1=D1,
∴平面BDF∥平面B1D1H.
备选例题
如图,在四棱锥S—ABCD中,底面ABCD为正方形,E,F分别为AB,SC的中点,求证:EF∥平面SAD.
【思路探究】 可以取SD的中点G连GF、AG构成平行四边形,从而找到平行于EF并且在平面SAD内的直线.
【自主解答】 取SD的中点G,连接GF、AG.
又∵F为SC的中点.
∴GF为△SDC的中位线.
∴GF平行并等于DC.
又E为AB的中点且底面ABCD为正方形.
∴AE平行并等于CD.∴GF平行并等于AE.
∴四边形AEFG为平行四边形.
∴EF∥AG.又AG 平面SAD,EF平面SAD,
∴EF∥平面SAD.
规律方法
利用线面平行的性质定理时,应先确定线面平行,再寻找过已知直线的平面与平面相交的交线,然后确定线线平行,证题时应认真领悟线线平行与线面平行的相互转化关系.
备选变式
如图,在直三棱柱ABC—A1B1C1中,AC=BC,点D是AB的中点,求证:AC1∥平面CDB1.
【证明】 如图,连接BC1,设BC1与B1C的交点为E,连接DE.
∴D是AB的中点,E是BC1的中点,
∴DE∥AC1.
∵DE 平面CDB1,
AC1平面CDB1,
∴AC1∥平面CDB1.
平行关系
教案
●三维目标
1.知识与技能
(1)理解直线与平面平行、平面与平面平行的判定定理的含义.(2)会判断线面、面面平行.
2.过程与方法
通过观察图形,借助已有知识,掌握线面、面面平行的判定定理,培养学生观察发现的能力和空间想象能力.
3.情感、态度与价值观
(1)让学生在发现中学习,增强学习的积极性.
(2)让学生了解空间与平面互相转换的数学思想.
●重点难点
重点:线面、面面平行的判定定理.
难点:利用平行的判定定理证明平行关系.
●教学建议
讲解平行关系时,教师可以从身边的实物为例引导学生去认识平行关系的判定,如观察书的边缘与书面的位置等,让学生在情景中学会感知,得出结论,教学中,可以让学生观察具体的长方体实物模型,以增强对判定定理的直观感知.
●教学流程
创设问题情境,引出两个问题:直线与平面、平面与平面的关系 引导学生通过观察回答问题,引出直线与平面平行、平面与平面平行的判定定理 通过例1及互动探究,使学生掌握直线平面平行的证明问题 通过例2及变式训练,使学生掌握,平面与平面平行的证明问题 通过例3及变式训练,使学生掌握,直线平面、平面平面平行的综合问题 归纳整合本节知识,作课堂小结 让学生完成当堂双基达标,巩固所学知识,反馈并矫正
课标解读
1.理解直线与平面平行、平面与平面平行的判定定理的含义,会判断线面、面面平行(重点).2.会用图形语言、文字语言、符号语言准确描述直线与平面平行、平面与平面平行的判定定理,并知道其地位和作用(难点).
知识1
直线和平面平行的判定定理
【问题导思】
教室的门通过门轴可以自由的开关,在开关的过程中,门上竖直的一边与门轴所在边什么关系?与门轴所在墙面又是什么关系?
【提示】 门上竖直的一边与门轴所在边平行,与墙面也平行.
知识2
平面与平面平行的判定定理
【问题导思】
三角板的一边所在直线与桌面平行,这个三角板所在平面与桌面平行吗?三角板的两条边所在直线分别与桌面平行,情况又如何呢?
【提示】 三角板的一条边所在直线与桌面平行时,三角板所在平面与桌面可能平行,也可能相交.三角板的两条边所在直线分别与桌面平行时,三角板所在平面与桌面平行.
类型1
线面平行的判定
例1 如图1-5-1,四边形ABCD,ADEF都是正方形,M∈BD,N∈AE,且BM=AN.
图1-5-1
求证:MN∥平面CED.
【思路探究】 要证明MN∥平面CED,需在平面CED中找一条直线平行于MN,进而转化为线线平行的证明.
【自主解答】 如图,连接AM并延长交CD于点G,连接GE,
因为AB∥CD,所以=.
所以=,
即=.
又因为BD=AE且AN=BM,
所以=.所以MN∥GE.
又GE 平面CED,MN平面CED,
所以MN∥平面CED.
规律方法
1.本题也可通过过M、N分别作AD的平行线构造平行四边形来寻找平行线证明.
2.线面平行的判定方法
(1)利用定义证线面无公共点.
(2)利用线面平行的判定定理,将线线平行转化为线面平行.
互动探究
本例条件不变,求证:BF∥平面CDE.
【证明】 ∵四边形ABCD,ADEF都是正方形,
∴BC平行并等于AD平行并等于EF,∴BC平行并等于EF.
∴四边形BCEF是平行四边形,∴BF∥CE.
∵BF平面CDE,CE 平面CDE,∴BF∥平面CDE.
类型2
面面平行的判定
例2 已知四棱锥P—ABCD中,底面ABCD为平行四边形.点M、N、Q分别在PA、BD、PD上,且PM∶MA=BN∶ND=PQ∶QD.
图1-5-2
求证:平面MNQ∥平面PBC.
【思路探究】 (1)你认为证明线面平行、面面平行关键是什么?
(2)题中所给成比例线段有什么用?
(3)能否找到两条相交直线都和平面PBC平行?
【自主解答】 ∵PM∶MA=BN∶ND=PQ∶QD,
∴MQ∥AD,NQ∥BP.
∵BP 平面PBC,NQ平面PBC,
∴NQ∥平面PBC.
又底面ABCD为平行四边形,
∴BC∥AD,
∴MQ∥BC.
∵BC 平面PBC,MQ平面PBC,
∴MQ∥平面PBC.
又MQ∩NQ=Q,根据平面与平面平行的判定定理,得平面MNQ∥平面PBC.
规律方法
1.利用比例线段推出平行关系是解答本题的关键.
2.面面平行的判定方法
(1)利用定义,证面面无公共点.
(2)利用面面平行的判定定理转化为证明线面平行,即证明一个平面内的两条相交直线平行于另一个平面.
变式训练
图1-5-3
如图1-5-3在正方体ABCD-A1B1C1D1中,M、N、P分别是CC1、B1C1、C1D1的中点.
求证:平面MNP∥平面A1BD.
【证明】 如图所示,连接B1D1,
∵P、N分别是D1C1、B1C1的中点,
∴PN∥B1D1.
又B1D1∥BD,
∴PN∥BD,又PN平面A1BD,
BD 平面A1BD,
∴PN∥平面A1BD,
同理可得MN∥平面A1BD,
又∵MN∩PN=N,∴平面PMN∥平面A1BD.
类型3
平行关系的综合应用
例3 如图1-5-4,在正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,
图1-5-4
问:当点Q在什么位置时,平面D1BQ∥平面PAO?
【思路探究】 (1)由条件“P是DD1中点”,你猜想Q应在CC1的什么位置?
(2)PO与BD1平行吗?
【自主解答】 Q为CC1的中点时,平面D1BQ∥平面PAO.证明如下:
设Q为CC1中点,
则PD平行并等于QC,连接PQ,则由PQ平行并等于DC平行并等于AB,
可知四边形ABQP是平行四边形,
∴AP∥BQ.
∵AP平面D1BQ,BQ 平面D1BQ,
∴AP∥平面D1BQ.
∵O、P分别为BD、DD1的中点,∴OP∥BD1.
又OP
平面D1BQ,BD1 平面D1BQ,
∴OP∥平面D1BQ.
又AP∩PO=P,∴平面D1BQ∥平面PAO,
∴当点Q为CC1的中点时,平面D1BQ∥平面PAO.
规律方法
1.本题中由条件P是DD1中点猜想到Q应是CC1的中点是解题的关键.
2.对于条件缺失的探索性问题,解答过程中要明确目的,结合题目本身的特点与相应的定理大胆地猜想,然后加以证明.特别要注意中点、顶点等特殊点.
变式训练
如图1-5-5,正三棱柱ABC—A1B1C1的底面边长为2,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的点,EC=2FB=2.则当点M在什么位置时,MB∥平面AEF?试给出证明.
图1-5-5
【解】 当M为AC中点时,
MB∥平面AEF.
证明 如图,当M为AC中点时,过M作MG∥CE,交AE于G,连接GF.
∵M为AC中点,
∴MG平行并等于CE.
又FB∥CE,EC=2FB,
∴MG平行并等于FB.
∴四边形BFGM为平行四边形,
∴GF∥MB.
又GF 平面AEF,MB平面AEF,所以MB∥平面AEF.
忽视判定定理中的条件致误
典例 如图1-5-6,在正方体ABCD—A1B1C1D1中,M∈AD1,N∈BD,且D1M=DN,求证:MN∥平面CC1D1D.
【错解】 连AN并延长交DC于E,连接D1E
∵AB∥CD,
∴= =,
∵BD=AD1,D1M=DN,
∴=,∴MN∥D1E,
∴MN∥平面CC1D1D.
【错因分析】 忽视了直线与平面平行的判定定理中“lα,b α”这一条件,致使定理不完整.
【防范措施】 判定定理中的各个条件都不能忽视不能遗漏.
【正解】 连AN并延长交DC于E.连接D1E.
∵AB∥CD,
∴= =.
∵BD=AD1,
且D1M=DN,
∴=.
在△AD1E中,MN∥D1E,
又MN平面CC1D1D,D1E 平面CC1D1D,
∴MN∥平面CC1D1D.
1.直线与平面平行的关键是在已知平面内找一条直线和已知直线平行,即要证直线与平面平行,先证直线与直线平行.即由立体向平面转化,由高维向低维转化.
2.证明面面平行时,要按“线线平行”、“线面平行”、“面面平行”的证明顺序进行.当题目中有多个平面平行时,要注意平行平面的传递性.两平面平行的判定定理的条件中直线相交很重要,而且在解题中常常被忽视.
1.能保证直线a与平面α平行的条件是( )
A.aα,b α,a∥b
B.b α,a∥b
C.b α,c α,a∥c,且a∥b
D.b α,A∈a,B∈a,C∈b,D∈b,且AC=BD
【解析】 B、C、D均可能有a在平面α内.
【答案】 A
2.直线l,m,平面α、β,l α,m α,l∥β,m∥β,则α与β的位置关系是( )
A.平行
B.相交
C.异面
D.不确定
【解析】 α与β可能相交,也可能平行.
【答案】 D
3.已知两条相交直线a,b,且a∥平面α,则b与α的位置关系是________.
【解析】 由图可知,b与α平行或相交.
【答案】 平行或相交
图1-5-7
4.四棱锥P—ABCD中,AB=AD,∠BAD=60°,CD⊥AD,F,E分别是PA,AD的中点,求证:
平面PCD∥平面FEB.
【证明】 连接BD,在△ABD中,∠BAD=60°,AB=AD,
∴△ABD是等边三角形,E为AD的中点,
∴BE⊥AD.
又CD⊥AD,
∴在四边形ABCD中,BE∥CD.
又CD平面FEB,
BE 平面FEB,
∴CD∥平面FEB.
在△APD中,EF∥PD,
同理可得PD∥平面FEB.
又CD∩PD=D,
∴平面PCD∥平面FEB.
一、选择题
1.下列说法正确的是( )
A.平行于同一个平面的两条直线平行
B.同时与两异面直线平行的平面有无数多个
C.如果一条直线上有两点在一个平面外,则这条直线与这个平面平行
D.直线l不在平面α内,则l∥α
【解析】 A选项,若两直线相交且同时与此平面平行也是可以的;B选项,我们将异面直线都平移到空间中的某一点相交,则它们确定一个平面,与此平面平行的平面平行于这两条异面直线,显然这样的平面有无穷多个;C、D选项,若直线与平面相交,则直线有两点在平面外,直线也不在平面内,但l与α不平行.
【答案】 B
2.若M,N分别是△ABC边AB,AC的中点,MN与过直线BC的平面β的位置关系是( )
A.MN∥β
B.MN与β相交或MN β
C.MN∥β或MN β
D.MN∥β或MN与β相交或MN β
【解析】 当平面β与平面ABC重合时,有MN β;当平面β与平面ABC不重合时,则β∩平面ABC=BC.
∵M,N分别为AB,AC的中点,∴MN∥BC.
又MN
β,BC β,∴MN∥β.综上有MN∥β或MN β.
【答案】 C
3.如果AB、BC、CD是不在同一平面内的三条线段,则经过它们中点的平面和直线AC的位置关系是( )
A.平行 B.相交
C.AC在此平面内
D.平行或相交
【解析】 如图:E、F、G分别为AB、BC、CD的中点.
∵E、F分别是AB,BC的中点,
∴EF∥AC.
又EF 平面EFG,且AC
平面EFG.
∴AC∥平面EFG.
【答案】 A
4.在正方体ABCD-A1B1C1D1中,下列四对截面中彼此平行的一对截面是( )
A.平面A1BC1和平面ACD1
B.平面BDC1和平面B1D1C
C.平面B1D1D和平面BDA1
D.平面ADC1和平面AD1C
【解析】 如图,在截面A1BC1和截面AD1C中,
平面A1BC1∥平面ACD1.
【答案】 A
图1-5-8
5.如图1-5-8,在空间四边形ABCD中,E、F分别为边AB、AD上的点,且AE∶EB=AF∶FD=1∶4,又H、G分别为BC、CD的中点,则( )
A.BD∥平面EFGH,且四边形EFGH是矩形
B.EF∥平面BCD,且四边形EFGH是梯形
C.HG∥平面ABD,且四边形EFGH是菱形
D.EH∥平面ADC,且四边形EFGH是梯形
【解析】 ∵AE∶EB=AF∶FD=1∶4,
∴EF∥BD且EF=BD.
又H、G分别为BC、CD的中点,
∴HG平行并等于BD.
∴EF∥HG且EF≠HG.
∴四边形EFGH为梯形.
∵BD 平面BCD且EF
平面BCD.
∴EF∥平面BCD.
【答案】 B
二、填空题
图1-5-9
6.如图1-5-9所示,在空间四边形ABCD中,M∈AB,N∈AD,若=,则MN与平面BDC的位置关系是________.
【解析】 ∵=,∴MN∥BD.
又∵MN
平面BDC,BD 平面BDC,
∴MN∥平面BDC.
【答案】 平行
7.已知a、b、c为三条不重合的直线,α,β,γ为三个不重合平面,下面三个命题:
①a∥c,b∥c a∥b;②γ∥α,β∥α γ∥β;③a∥γ,α∥γ a∥α.
其中正确命题的序号是________.
【解析】 由平行公理,知①正确;由平面平行的传递性知②正确;③不正确,因为a可能在α内.
【答案】 ①②
8.在空间四边形PABC中,A1、B1、C1分别是△PBC、△PCA、△PAB的重心,则平面ABC与平面A1B1C1的位置关系是________.
【解析】 如图,连接PC1,PA1,并延长分别交AB,BC于E、F两点,由于C1、A1分别为重心.
∴E、F分别为AB、BC的中点,连接EF.
又∵==2.
∴A1C1∥EF.
又∵EF为△ABC边AC上的中位线,
∴EF∥AC,∴AC∥A1C1,
又A1C1 平面ABC,AC?平面ABC,
∴A1C1∥平面ABC,
同理A1B1∥平面ABC,
A1B1∩A1C1=A1,
∴平面A1B1C1∥平面ABC.
【答案】 平行
三、解答题
9.在三棱柱ABC—A′B′C′中,点E,D分别是B′C′与BC的中点.求证:平面A′EB∥平面ADC′.
【证明】 连接DE,
∵E,D分别是B′C′与BC的中点,
∴DE平行并等于AA′,
∴AA′ED是平行四边形,∴A′E∥AD.
∵A′E
平面ADC′,AD 平面ADC′.
∴A′E∥平面ADC′.
又BE∥DC′,BE
平面ADC′,DC′ 平面ADC′,
∴BE∥平面ADC′,
∵A′E 平面A′EB,BE 平面A′EB,
A′E∩BE=E,
∴平面A′EB∥平面ADC′.
图1-5-10
10.如图1-5-10,在直四棱柱ABCD-A1B1C1D1中,底面是梯形,AB∥CD,CD=2AB,P、Q分别是CC1、C1D1的中点,求证:面AD1C∥面BPQ.
【证明】 ∵D1Q=DC,AB平行并等于CD,∴D1Q
平行并等于AB.
∴四边形D1QBA为平行四边形,∴D1A平行并等于QB.
∵Q、P分别为D1C1、C1C的中点,∴QP∥D1C.
∵D1C∩D1A=D1,PQ∩QB=Q.
∴面AD1C∥面BPQ.
图1-5-11
11.如图1-5-11,E,F,G,H分别是正方体ABCD—A1B1C1D1的棱BC,CC1,C1D1,AA1的中点,求证:
(1)GE∥平面BB1D1D;
(2)平面BDF∥平面B1D1H.
【证明】 (1)取B1D1中点O,连接GO,OB,易证OG∥B1C1,
且OG=B1C1,BE∥B1C1,
且BE=B1C1,
∴OG∥BE且OG=BE,四边形BEGO为平行四边形,
∴OB∥GE.
∵OB
平面BDD1B1,
GE
平面BDD1B1,
∴GE∥平面BDD1B1.
(2)由正方体性质得
B1D1∥BD,
∵B1D1 平面BDF,BD 平面BDF,
∴B1D1∥平面BDF,连接HB,D1F,
易证HBFD1是平行四边形,得HD1∥BF.
∵HD1
平面BDF,BF 平面BDF,
∴HD1∥平面BDF,
∵B1D1∩HD1=D1,
∴平面BDF∥平面B1D1H.
备选例题
如图,在四棱锥S—ABCD中,底面ABCD为正方形,E,F分别为AB,SC的中点,求证:EF∥平面SAD.
【思路探究】 可以取SD的中点G连GF、AG构成平行四边形,从而找到平行于EF并且在平面SAD内的直线.
【自主解答】 取SD的中点G,连接GF、AG.
又∵F为SC的中点.
∴GF为△SDC的中位线.
∴GF平行并等于DC.
又E为AB的中点且底面ABCD为正方形.
∴AE平行并等于CD.∴GF平行并等于AE.
∴四边形AEFG为平行四边形.
∴EF∥AG.又AG 平面SAD,EF平面SAD,
∴EF∥平面SAD.
规律方法
利用线面平行的性质定理时,应先确定线面平行,再寻找过已知直线的平面与平面相交的交线,然后确定线线平行,证题时应认真领悟线线平行与线面平行的相互转化关系.
备选变式
如图,在直三棱柱ABC—A1B1C1中,AC=BC,点D是AB的中点,求证:AC1∥平面CDB1.
【证明】 如图,连接BC1,设BC1与B1C的交点为E,连接DE.
∴D是AB的中点,E是BC1的中点,
∴DE∥AC1.
∵DE 平面CDB1,
AC1平面CDB1,
∴AC1∥平面CDB1.
