1.5.1 平行关系的判定 同步练习1(含答案)
文档属性
| 名称 | 1.5.1 平行关系的判定 同步练习1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 368.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 16:36:03 | ||
图片预览

文档简介
1.5.1
平行关系的判定
同步练习
一、选择题(每小题4分,共16分)
1.若平面α和平面β相交于直线l,直线a在平面α内,但不与直线l重合,则直线a与平面β的位置关系是(
)
(A)相交
(B)平行
(C)相交或平行
(D)aβ
2.如图,下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是(
)
(A)①④
(B)②④
(C)①③④
(D)①③
3.过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有(
)
(A)4条
(B)6条
(C)8条
(D)12条
4.正方体ABCD-A1B1C1D1的棱长为1,E是AB的
中点,点F在BC上,则BF等于多少时,EF∥
平面A1C1D(
)
(A)1
(B)
(C)
(D)
二、填空题(每小题4分,共8分)
5.a,b,c是三条直线,α,β是两个平面,如果a∥b∥c,aα,
bβ,cβ,那么平面α与平面β的位置关系是_________
.
6.设m,n是平面α外的两条直线,给出三个说法:
①m∥n;②m∥α;③n∥α,以其中两个为条件,余下的一个为结论,可构成三个命题,写出你认为正确的一个命题__________.
三、解答题(每小题8分,共16分)
7.(易错题)不共面的三条线段AA1,BB1,CC1交于一点O且被O所平分,求证:平面ABC∥平面A1B1C1.
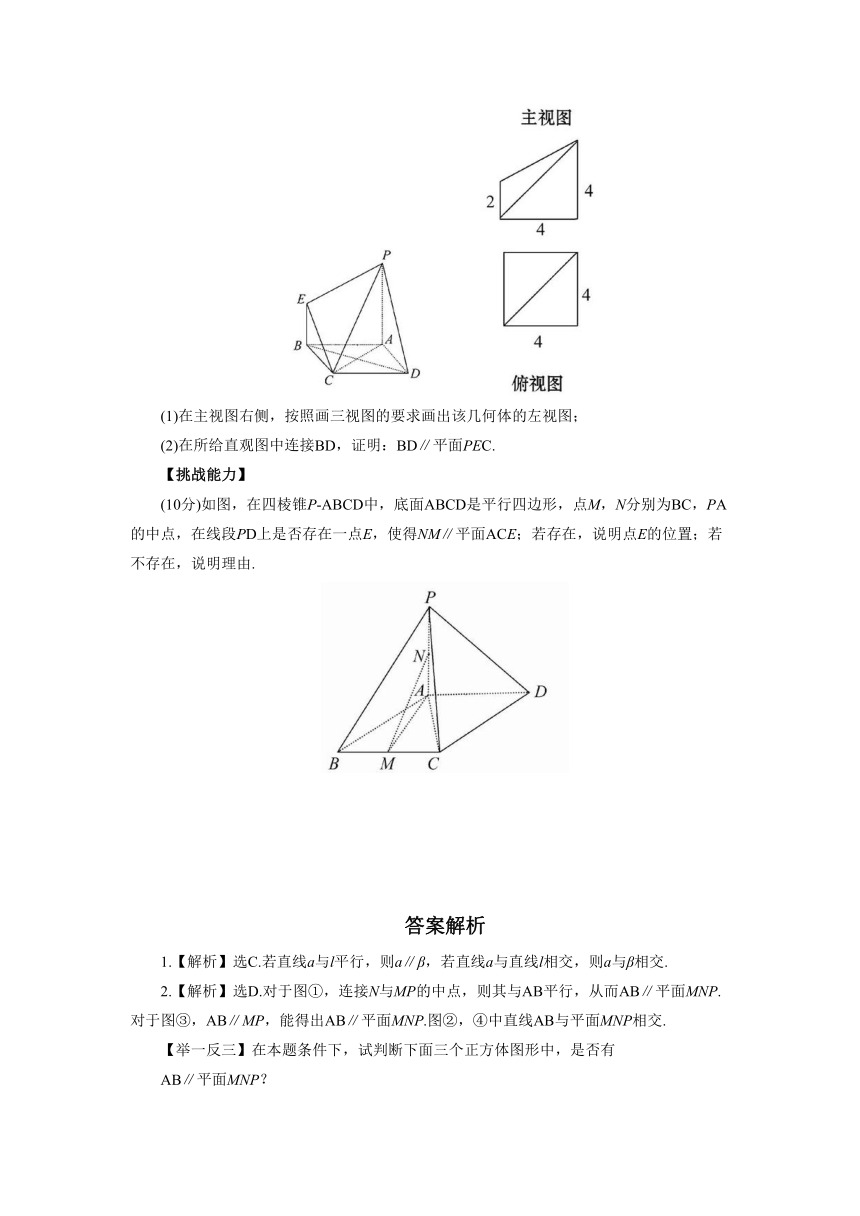
8.如图是一几何体的直观图,主视图和俯视图.
(1)在主视图右侧,按照画三视图的要求画出该几何体的左视图;
(2)在所给直观图中连接BD,证明:BD∥平面PEC.
【挑战能力】
(10分)如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M,N分别为BC,PA的中点,在线段PD上是否存在一点E,使得NM∥平面ACE;若存在,说明点E的位置;若不存在,说明理由.
答案解析
1.【解析】选C.若直线a与l平行,则a∥β,若直线a与直线l相交,则a与β相交.
2.【解析】选D.对于图①,连接N与MP的中点,则其与AB平行,从而AB∥平面MNP.对于图③,AB∥MP,能得出AB∥平面MNP.图②,④中直线AB与平面MNP相交.
【举一反三】在本题条件下,试判断下面三个正方体图形中,是否有
AB∥平面MNP?
【解析】对于图①,取NP的中点为R,连接MR,则有AB∥MR且AB平面MNP,
所以AB∥平面MNP.
对于图③,AB∥NP,且AB平面MNP,NP平面MNP,
所以AB∥平面MNP.
图②中,AB与平面MNP相交.
所以,①③图中AB∥平面MNP.
3.【解析】选D.如图,设M,N,P,Q为所在棱
的中点,易知平面MNPQ∥平面DBB1D1,则过M,
N,P,Q这四个点中的任意两点的直线与平面DBB1D1
平行,这种情形共有6条;同理,经过BC,CD,B1C1,
C1D1四条棱的中点也有6条,故共有12条.
4.【解析】选B.当点F是BC的中点时,即BF=BC=,有EF∥平面A1C1D.
∵EF∥AC,AC∥A1C1,∴EF∥A1C1,
又∵EF
平面A1C1D,A1C1
平面A1C1D,
∴EF∥平面A1C1D.
5.【解题指南】借助于正方体模型来判断.
【解析】由正方体模型易知α∥β或α与β相交.
答案:平行或相交
6.【解题指南】先列出三个命题,然后判断真假.
【解析】三个命题如下:(1)m∥n,m∥α n∥α;
(2)m∥n,n∥α m∥α;
(3)m∥α,n∥α m∥n.
经验证,(1)(2)正确,(3)中m与n可能相交、平行、异面.
答案:①② ③(或①③ ②)
7.【证明】如图,因AA1∩CC1=O,所以AA1与CC1确定一个平面,
设为平面α.
又∵△AOC≌△A1OC1,
∴∠OAC=∠OA1C1,从而AC∥A1C1.
又A1C1
平面A1B1C1,
AC
平面A1B1C1,由线面平行的判定定
理得AC∥平面A1B1C1.
同理AB∥平面A1B1C1.又AB∩AC=A,AB
平面ABC,AC
平面ABC,
由面面平行的判定定理得平面ABC∥平面A1B1C1.
8.【解析】(1)如图所示:
(2)取PC的中点M,设AC与BD的交点为N,连接MN,ME,
∵PM=CM,AN=CN,
∴MN=PA,MN∥PA,
∴MN=EB,MN∥EB,
故BEMN是平行四边形,
∴EM∥BN.又EM
平面PEC,BD
平面PEC,
∴BD∥平面PEC.
【方法技巧】线面平行证法面面观
在点、线、面的位置关系中,线面平行是重要的位置关系,也是我们学习的重点.在证明线面平行的过程中,关键是如何找线线平行,其方法主要有借助对应线段成比例、中位线、平行四边形等方法.下面主要就线面平行的证法进行归类总结.
(1)借助对应线段成比例
借助对应线段成比例来证明两直线平行,进而证明线面平行.
(2)借助中位线
借助三角形或梯形的中位线可以找到线线平行关系,从而证明线面平行.
(3)借助平行四边形
对于平行四边形我们知道其对边平行,借助此关系可以证明线面平行.
【挑战能力】
【解析】存在.取PD的中点E,连接NE,EC,AE,
因为N,E分别为PA,PD的中点,所以NE∥AD且
NE=AD.又在平行四边形ABCD中,CM∥AD且CM=AD,
所以NE
MC,即四边形MCEN是平行四边形,所以
NM∥EC,又EC
平面ACE,NM
平面ACE,
所以MN∥平面ACE,
即在PD上存在一点E,使得NM∥平面ACE,
此时PE=PD.
平行关系的判定
同步练习
一、选择题(每小题4分,共16分)
1.若平面α和平面β相交于直线l,直线a在平面α内,但不与直线l重合,则直线a与平面β的位置关系是(
)
(A)相交
(B)平行
(C)相交或平行
(D)aβ
2.如图,下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是(
)
(A)①④
(B)②④
(C)①③④
(D)①③
3.过平行六面体ABCD-A1B1C1D1任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有(
)
(A)4条
(B)6条
(C)8条
(D)12条
4.正方体ABCD-A1B1C1D1的棱长为1,E是AB的
中点,点F在BC上,则BF等于多少时,EF∥
平面A1C1D(
)
(A)1
(B)
(C)
(D)
二、填空题(每小题4分,共8分)
5.a,b,c是三条直线,α,β是两个平面,如果a∥b∥c,aα,
bβ,cβ,那么平面α与平面β的位置关系是_________
.
6.设m,n是平面α外的两条直线,给出三个说法:
①m∥n;②m∥α;③n∥α,以其中两个为条件,余下的一个为结论,可构成三个命题,写出你认为正确的一个命题__________.
三、解答题(每小题8分,共16分)
7.(易错题)不共面的三条线段AA1,BB1,CC1交于一点O且被O所平分,求证:平面ABC∥平面A1B1C1.
8.如图是一几何体的直观图,主视图和俯视图.
(1)在主视图右侧,按照画三视图的要求画出该几何体的左视图;
(2)在所给直观图中连接BD,证明:BD∥平面PEC.
【挑战能力】
(10分)如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M,N分别为BC,PA的中点,在线段PD上是否存在一点E,使得NM∥平面ACE;若存在,说明点E的位置;若不存在,说明理由.
答案解析
1.【解析】选C.若直线a与l平行,则a∥β,若直线a与直线l相交,则a与β相交.
2.【解析】选D.对于图①,连接N与MP的中点,则其与AB平行,从而AB∥平面MNP.对于图③,AB∥MP,能得出AB∥平面MNP.图②,④中直线AB与平面MNP相交.
【举一反三】在本题条件下,试判断下面三个正方体图形中,是否有
AB∥平面MNP?
【解析】对于图①,取NP的中点为R,连接MR,则有AB∥MR且AB平面MNP,
所以AB∥平面MNP.
对于图③,AB∥NP,且AB平面MNP,NP平面MNP,
所以AB∥平面MNP.
图②中,AB与平面MNP相交.
所以,①③图中AB∥平面MNP.
3.【解析】选D.如图,设M,N,P,Q为所在棱
的中点,易知平面MNPQ∥平面DBB1D1,则过M,
N,P,Q这四个点中的任意两点的直线与平面DBB1D1
平行,这种情形共有6条;同理,经过BC,CD,B1C1,
C1D1四条棱的中点也有6条,故共有12条.
4.【解析】选B.当点F是BC的中点时,即BF=BC=,有EF∥平面A1C1D.
∵EF∥AC,AC∥A1C1,∴EF∥A1C1,
又∵EF
平面A1C1D,A1C1
平面A1C1D,
∴EF∥平面A1C1D.
5.【解题指南】借助于正方体模型来判断.
【解析】由正方体模型易知α∥β或α与β相交.
答案:平行或相交
6.【解题指南】先列出三个命题,然后判断真假.
【解析】三个命题如下:(1)m∥n,m∥α n∥α;
(2)m∥n,n∥α m∥α;
(3)m∥α,n∥α m∥n.
经验证,(1)(2)正确,(3)中m与n可能相交、平行、异面.
答案:①② ③(或①③ ②)
7.【证明】如图,因AA1∩CC1=O,所以AA1与CC1确定一个平面,
设为平面α.
又∵△AOC≌△A1OC1,
∴∠OAC=∠OA1C1,从而AC∥A1C1.
又A1C1
平面A1B1C1,
AC
平面A1B1C1,由线面平行的判定定
理得AC∥平面A1B1C1.
同理AB∥平面A1B1C1.又AB∩AC=A,AB
平面ABC,AC
平面ABC,
由面面平行的判定定理得平面ABC∥平面A1B1C1.
8.【解析】(1)如图所示:
(2)取PC的中点M,设AC与BD的交点为N,连接MN,ME,
∵PM=CM,AN=CN,
∴MN=PA,MN∥PA,
∴MN=EB,MN∥EB,
故BEMN是平行四边形,
∴EM∥BN.又EM
平面PEC,BD
平面PEC,
∴BD∥平面PEC.
【方法技巧】线面平行证法面面观
在点、线、面的位置关系中,线面平行是重要的位置关系,也是我们学习的重点.在证明线面平行的过程中,关键是如何找线线平行,其方法主要有借助对应线段成比例、中位线、平行四边形等方法.下面主要就线面平行的证法进行归类总结.
(1)借助对应线段成比例
借助对应线段成比例来证明两直线平行,进而证明线面平行.
(2)借助中位线
借助三角形或梯形的中位线可以找到线线平行关系,从而证明线面平行.
(3)借助平行四边形
对于平行四边形我们知道其对边平行,借助此关系可以证明线面平行.
【挑战能力】
【解析】存在.取PD的中点E,连接NE,EC,AE,
因为N,E分别为PA,PD的中点,所以NE∥AD且
NE=AD.又在平行四边形ABCD中,CM∥AD且CM=AD,
所以NE
MC,即四边形MCEN是平行四边形,所以
NM∥EC,又EC
平面ACE,NM
平面ACE,
所以MN∥平面ACE,
即在PD上存在一点E,使得NM∥平面ACE,
此时PE=PD.
