1.5.1 平行关系的判定 学案(含答案)
文档属性
| 名称 | 1.5.1 平行关系的判定 学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 16:40:15 | ||
图片预览



文档简介
1.5.1
平行关系的判定
学案
问题导学
1.对平行关系的理解
活动与探究1
判断下列给出的各种说法是否正确?
(1)如果直线a和平面α不相交,那么a∥α;
(2)如果直线a∥平面α,直线b∥a,那么b∥α;
(3)如果直线a∥平面α,那么经过直线a的平面β∥α;
(4)如果平面α内的两条相交直线a和b与平面β内的两条相交直线a′和b′分别平行,那么α∥β.
迁移与应用
1.下列叙述中,正确的是( ).
A.若直线l平行于平面α内的无数条直线,则l∥α
B.若直线a在平面α外,则a∥α
C.若直线a∥b,直线bα,则a∥α
D.若直线a∥b,bα,那么直线a平行于平面α内的无数条直线
2.两个平面平行的条件是( ).
A.一个平面内的一条直线平行于另一平面
B.一个平面内有两条直线平行于另一平面
C.一个平面内有无数条直线平行于另一个平面
D.一个平面内任何一条直线平行于另一个平面
名师点津
1.要全面、深刻地理解线面平行、面面平行的判定定理,运用这两个定理证明问题或判断分析结论是否正确时,一定要紧扣两个定理的条件,忽视条件,很容易导致判断错误.
2.在判断一些命题的真假时,要善于列举反例来否定一个命题,要充分考虑线线关系、线面关系、面面关系中的各种情形,以对一个命题的真假作出合理的判断.
2.直线与平面平行的判定
活动与探究2
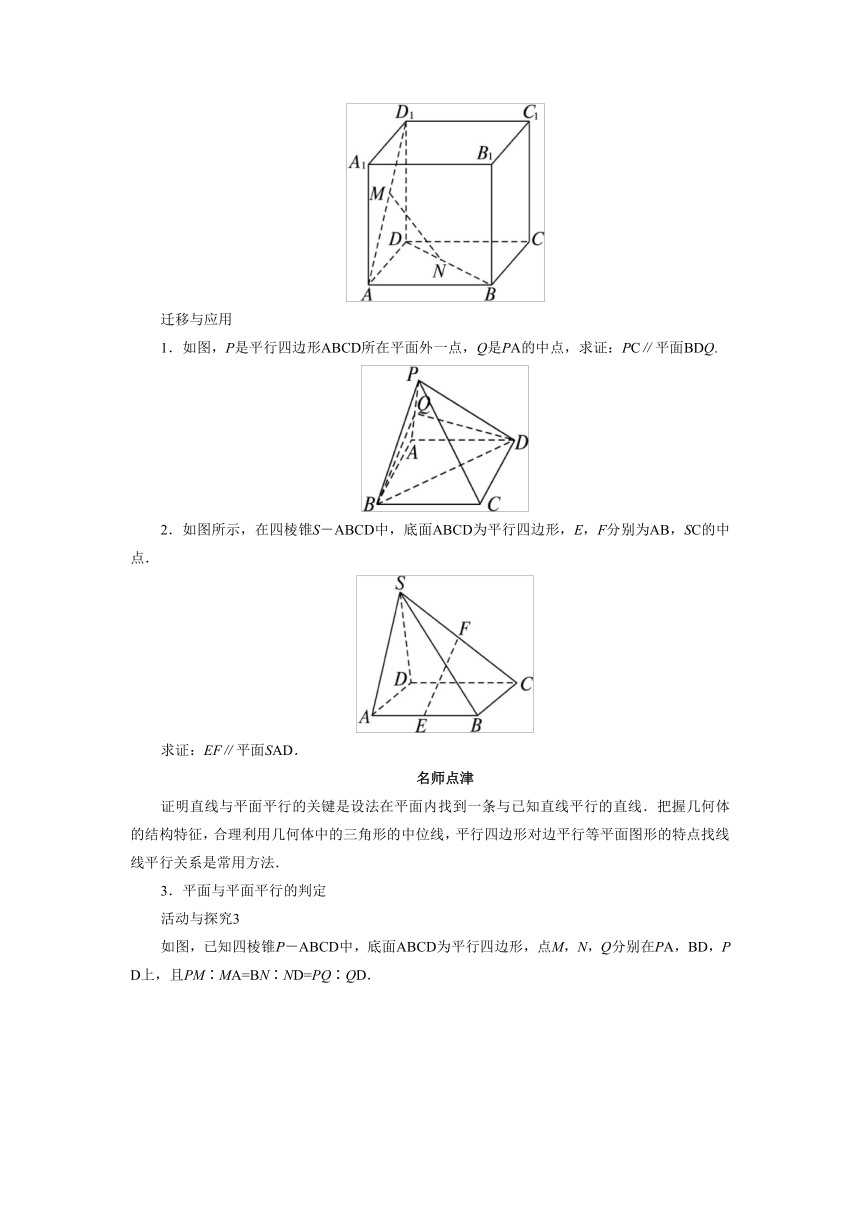
如右图,在正方体ABCD-A1B1C1D1中,M∈AD1,N∈BD,且D1M=DN,求证:MN∥平面CC1D1D.
迁移与应用
1.如图,P是平行四边形ABCD所在平面外一点,Q是PA的中点,求证:PC∥平面BDQ.
2.如图所示,在四棱锥S-ABCD中,底面ABCD为平行四边形,E,F分别为AB,SC的中点.
求证:EF∥平面SAD.
名师点津
证明直线与平面平行的关键是设法在平面内找到一条与已知直线平行的直线.把握几何体的结构特征,合理利用几何体中的三角形的中位线,平行四边形对边平行等平面图形的特点找线线平行关系是常用方法.
3.平面与平面平行的判定
活动与探究3
如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD.
求证:平面MNQ∥平面PBC.
迁移与应用
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,G分别是CB,CD,CC1的中点.
求证:平面AB1D1∥平面EFG.
名师点津
证明面面平行的基本思想是将面面平行转化为线面平行,其基本步骤是:线线平行 线面平行 面面平行.但必须注意的是:在其中一个面内找到的两条直线必须是相交直线,且这两条相交直线都与另一个平面平行时,这两个平面才平行.
当堂检测
1.若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( ).
A.一定平行
B.一定相交
C.平行或相交
D.以上都不对
2.A,B是不在直线l上的两点,则过点A,B且与直线l平行的平面的个数是( ).
A.0
B.1
C.无数
D.以上三种情况均有可能
3.梯形ABCD中,AB∥CD,ABα,CDα,则直线CD与平面α的位置关系是__________.
4.如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F分别是PB,PC的中点.证明EF∥平面PAD.
5.如图所示,在正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点.求证:平面AMN∥平面EFDB.
盘点收获
提示:用最精练的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记.
答案:
课前预习导学
预习导引
1.(1)一条直线平行
预习交流1 提示:直线a平面α是指a∥α或a与α相交.
预习交流2 提示:不正确.不符合线面平行的判定定理,只有当直线l在平面α外,且与平面α内的一条直线平行时,直线l才与平面平行.
预习交流3 提示:(1)线面平行的判定定理表明可以通过直线间的平行,推证直线与平面平行.这是处理空间问题的一种常用方法,即将直线与平面的平行关系转化为直线与直线的平行关系,把空间问题平面化.
(2)线面平行的判定定理在使用时三个条件缺一不可:
①直线a不在平面α内,即aα;
②直线b在平面α内,即bα;
③两条直线a,b平行,即a∥b.
2.(1)两条相交直线
预习交流4 提示:不一定,平面α与平面β相交或平行.
预习交流5 提示:一定平行.由直线与平面平行的判定定理知,平面α内的两条相交直线与平面β都平行,再由面面平行的判定定理可得α∥β.
课堂合作探究
问题导学
活动与探究1 思路分析:按照线面平行、面面平行的定义及判定定理对每个命题进行分析判断,得出其是否正确.
解:(1)不正确.当直线a和平面α不相交时,可能有aα,不一定有a∥α;
(2)不正确.当直线b∥a时,如果bα,则有b∥α,如果bα,则没有b∥α;
(3)不正确.当a∥α时,经过直线a的平面β可能与α平行,也可能与α相交;
(4)正确.由线面平行的判定定理,知a∥β,b∥β,且a,bα,a与b相交,所以必有α∥β.
迁移与应用 1.D 解析:当a∥b,bα时,不论a∥α还是aα,a都平行于平面α内的无数条直线,故选项D正确.
2.D 解析:因一个平面内任何一条直线平行于另一个平面,可在这个平面内选两条相交直线,则这两条相交直线都与另一平面平行,由平面与平面平行的判定定理可得两个平面平行.
活动与探究2 思路分析:要证MN∥平面CC1D1D,只需证明MN平行于平面CC1D1D中的一条直线即可.
证明:方法一:连接AN并延长,交直线CD于E,连接D1E.
∵AB∥CD,
∴= =.
∵BD=AD1,且D1M=DN,
∴=.
在△AD1E中,MN∥D1E,
又MN平面CC1D1D,D1E平面CC1D1D,
∴MN∥平面CC1D1D.
方法二:过点M作MP∥AD,交DD1于P,
过点N作NQ∥AD交CD于点Q,连接PQ,
则MP∥NQ,在△D1AD中,=.
∵NQ∥AD,AD∥BC,
∴NQ∥BC.
在△DBC中,=,
∵D1M=DN,D1A=DB,AD=BC,∴NQ=MP.
∴四边形MNQP为平行四边形,
则MN∥PQ.
而MN平面CC1D1D,PQ平面CC1D1D,
∴MN∥平面CC1D1D.
迁移与应用 1.证明:连接AC交BD于O,连接QO.
∵四边形ABCD是平行四边形,
∴O为AC的中点.
又Q为PA的中点,∴QO∥PC.
显然QO平面BDQ,PC平面BDQ,
∴PC∥平面BDQ.
2.证明:作FG∥DC交SD于点G,则G为SD的中点.
连接AG,FGCD,
又CDAB,且E为AB的中点,
故FGAE,四边形AEFG为平行四边形.∴EF∥AG.
又∵AG平面SAD,EF平面SAD,∴EF∥平面SAD.
活动与探究3 思路分析:在平面MNQ内找到两条相交直线与平面PBC平行,条件中给出了线段比相等,故可利用平行线截线段成比例的性质证得线线平行,再转化为线面平行,然后根据面面平行的判定定理证明.
证明:在△PAD中,
∵PM∶MA=PQ∶QD,
∴MQ∥AD.
又∵AD∥BC,∴MQ∥BC.
∵MQ平面PBC,BC平面PBC,∴MQ∥平面PBC.
在△PBD中,
∵BN∶ND=PQ∶QD,
∴NQ∥PB.∵NQ平面PBC,PB平面PBC,
∴NQ∥平面PBC.
∵MQ∩NQ=Q,
∴平面MNQ∥平面PBC.
迁移与应用 证明:在正方体ABCD-A1B1C1D1中,连接BD,
∵DD1∥B1B,DD1=B1B,
∴四边形DD1B1B为平行四边形,∴D1B1∥DB.
∵E,F分别为BC,CD的中点,
∴EF∥BD,∴EF∥D1B1.
∵EF平面EFG,D1B1平面EFG,∴D1B1∥平面EFG.
同理AB1∥平面EFG.
∵D1B1∩AB1=B1,∴平面AB1D1∥平面EFG.
当堂检测
1.C 2.D 3.平行
4.证明:在△PBC中,
∵E,F分别是PB,PC的中点,
∴EF∥BC.
∵四边形ABCD为矩形,
∴BC∥AD,∴EF∥AD.
又∵AD平面PAD,EF平面PAD,∴EF∥平面PAD.
5.证明:如图所示,连接MF.
∵M,F分别是A1B1,C1D1的中点,且四边形A1B1C1D1为正方形,
∴MF∥A1D1,且MF=A1D1.
又∵A1D1=AD,且AD∥A1D1,
∴MF=AD,且MF∥AD.
∴四边形AMFD是平行四边形,
∴AM∥DF.
又DF平面EFDB,AM平面EFDB,∴AM∥平面EFDB.
同理可证,AN∥平面EFDB.
又AN,AM平面AMN,AM∩AN=A,∴平面AMN∥平面EFDB.
平行关系的判定
学案
问题导学
1.对平行关系的理解
活动与探究1
判断下列给出的各种说法是否正确?
(1)如果直线a和平面α不相交,那么a∥α;
(2)如果直线a∥平面α,直线b∥a,那么b∥α;
(3)如果直线a∥平面α,那么经过直线a的平面β∥α;
(4)如果平面α内的两条相交直线a和b与平面β内的两条相交直线a′和b′分别平行,那么α∥β.
迁移与应用
1.下列叙述中,正确的是( ).
A.若直线l平行于平面α内的无数条直线,则l∥α
B.若直线a在平面α外,则a∥α
C.若直线a∥b,直线bα,则a∥α
D.若直线a∥b,bα,那么直线a平行于平面α内的无数条直线
2.两个平面平行的条件是( ).
A.一个平面内的一条直线平行于另一平面
B.一个平面内有两条直线平行于另一平面
C.一个平面内有无数条直线平行于另一个平面
D.一个平面内任何一条直线平行于另一个平面
名师点津
1.要全面、深刻地理解线面平行、面面平行的判定定理,运用这两个定理证明问题或判断分析结论是否正确时,一定要紧扣两个定理的条件,忽视条件,很容易导致判断错误.
2.在判断一些命题的真假时,要善于列举反例来否定一个命题,要充分考虑线线关系、线面关系、面面关系中的各种情形,以对一个命题的真假作出合理的判断.
2.直线与平面平行的判定
活动与探究2
如右图,在正方体ABCD-A1B1C1D1中,M∈AD1,N∈BD,且D1M=DN,求证:MN∥平面CC1D1D.
迁移与应用
1.如图,P是平行四边形ABCD所在平面外一点,Q是PA的中点,求证:PC∥平面BDQ.
2.如图所示,在四棱锥S-ABCD中,底面ABCD为平行四边形,E,F分别为AB,SC的中点.
求证:EF∥平面SAD.
名师点津
证明直线与平面平行的关键是设法在平面内找到一条与已知直线平行的直线.把握几何体的结构特征,合理利用几何体中的三角形的中位线,平行四边形对边平行等平面图形的特点找线线平行关系是常用方法.
3.平面与平面平行的判定
活动与探究3
如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上,且PM∶MA=BN∶ND=PQ∶QD.
求证:平面MNQ∥平面PBC.
迁移与应用
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E,F,G分别是CB,CD,CC1的中点.
求证:平面AB1D1∥平面EFG.
名师点津
证明面面平行的基本思想是将面面平行转化为线面平行,其基本步骤是:线线平行 线面平行 面面平行.但必须注意的是:在其中一个面内找到的两条直线必须是相交直线,且这两条相交直线都与另一个平面平行时,这两个平面才平行.
当堂检测
1.若一个平面内的两条直线分别平行于另一个平面内的两条直线,则这两个平面的位置关系是( ).
A.一定平行
B.一定相交
C.平行或相交
D.以上都不对
2.A,B是不在直线l上的两点,则过点A,B且与直线l平行的平面的个数是( ).
A.0
B.1
C.无数
D.以上三种情况均有可能
3.梯形ABCD中,AB∥CD,ABα,CDα,则直线CD与平面α的位置关系是__________.
4.如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F分别是PB,PC的中点.证明EF∥平面PAD.
5.如图所示,在正方体ABCD-A1B1C1D1中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点.求证:平面AMN∥平面EFDB.
盘点收获
提示:用最精练的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记.
答案:
课前预习导学
预习导引
1.(1)一条直线平行
预习交流1 提示:直线a平面α是指a∥α或a与α相交.
预习交流2 提示:不正确.不符合线面平行的判定定理,只有当直线l在平面α外,且与平面α内的一条直线平行时,直线l才与平面平行.
预习交流3 提示:(1)线面平行的判定定理表明可以通过直线间的平行,推证直线与平面平行.这是处理空间问题的一种常用方法,即将直线与平面的平行关系转化为直线与直线的平行关系,把空间问题平面化.
(2)线面平行的判定定理在使用时三个条件缺一不可:
①直线a不在平面α内,即aα;
②直线b在平面α内,即bα;
③两条直线a,b平行,即a∥b.
2.(1)两条相交直线
预习交流4 提示:不一定,平面α与平面β相交或平行.
预习交流5 提示:一定平行.由直线与平面平行的判定定理知,平面α内的两条相交直线与平面β都平行,再由面面平行的判定定理可得α∥β.
课堂合作探究
问题导学
活动与探究1 思路分析:按照线面平行、面面平行的定义及判定定理对每个命题进行分析判断,得出其是否正确.
解:(1)不正确.当直线a和平面α不相交时,可能有aα,不一定有a∥α;
(2)不正确.当直线b∥a时,如果bα,则有b∥α,如果bα,则没有b∥α;
(3)不正确.当a∥α时,经过直线a的平面β可能与α平行,也可能与α相交;
(4)正确.由线面平行的判定定理,知a∥β,b∥β,且a,bα,a与b相交,所以必有α∥β.
迁移与应用 1.D 解析:当a∥b,bα时,不论a∥α还是aα,a都平行于平面α内的无数条直线,故选项D正确.
2.D 解析:因一个平面内任何一条直线平行于另一个平面,可在这个平面内选两条相交直线,则这两条相交直线都与另一平面平行,由平面与平面平行的判定定理可得两个平面平行.
活动与探究2 思路分析:要证MN∥平面CC1D1D,只需证明MN平行于平面CC1D1D中的一条直线即可.
证明:方法一:连接AN并延长,交直线CD于E,连接D1E.
∵AB∥CD,
∴= =.
∵BD=AD1,且D1M=DN,
∴=.
在△AD1E中,MN∥D1E,
又MN平面CC1D1D,D1E平面CC1D1D,
∴MN∥平面CC1D1D.
方法二:过点M作MP∥AD,交DD1于P,
过点N作NQ∥AD交CD于点Q,连接PQ,
则MP∥NQ,在△D1AD中,=.
∵NQ∥AD,AD∥BC,
∴NQ∥BC.
在△DBC中,=,
∵D1M=DN,D1A=DB,AD=BC,∴NQ=MP.
∴四边形MNQP为平行四边形,
则MN∥PQ.
而MN平面CC1D1D,PQ平面CC1D1D,
∴MN∥平面CC1D1D.
迁移与应用 1.证明:连接AC交BD于O,连接QO.
∵四边形ABCD是平行四边形,
∴O为AC的中点.
又Q为PA的中点,∴QO∥PC.
显然QO平面BDQ,PC平面BDQ,
∴PC∥平面BDQ.
2.证明:作FG∥DC交SD于点G,则G为SD的中点.
连接AG,FGCD,
又CDAB,且E为AB的中点,
故FGAE,四边形AEFG为平行四边形.∴EF∥AG.
又∵AG平面SAD,EF平面SAD,∴EF∥平面SAD.
活动与探究3 思路分析:在平面MNQ内找到两条相交直线与平面PBC平行,条件中给出了线段比相等,故可利用平行线截线段成比例的性质证得线线平行,再转化为线面平行,然后根据面面平行的判定定理证明.
证明:在△PAD中,
∵PM∶MA=PQ∶QD,
∴MQ∥AD.
又∵AD∥BC,∴MQ∥BC.
∵MQ平面PBC,BC平面PBC,∴MQ∥平面PBC.
在△PBD中,
∵BN∶ND=PQ∶QD,
∴NQ∥PB.∵NQ平面PBC,PB平面PBC,
∴NQ∥平面PBC.
∵MQ∩NQ=Q,
∴平面MNQ∥平面PBC.
迁移与应用 证明:在正方体ABCD-A1B1C1D1中,连接BD,
∵DD1∥B1B,DD1=B1B,
∴四边形DD1B1B为平行四边形,∴D1B1∥DB.
∵E,F分别为BC,CD的中点,
∴EF∥BD,∴EF∥D1B1.
∵EF平面EFG,D1B1平面EFG,∴D1B1∥平面EFG.
同理AB1∥平面EFG.
∵D1B1∩AB1=B1,∴平面AB1D1∥平面EFG.
当堂检测
1.C 2.D 3.平行
4.证明:在△PBC中,
∵E,F分别是PB,PC的中点,
∴EF∥BC.
∵四边形ABCD为矩形,
∴BC∥AD,∴EF∥AD.
又∵AD平面PAD,EF平面PAD,∴EF∥平面PAD.
5.证明:如图所示,连接MF.
∵M,F分别是A1B1,C1D1的中点,且四边形A1B1C1D1为正方形,
∴MF∥A1D1,且MF=A1D1.
又∵A1D1=AD,且AD∥A1D1,
∴MF=AD,且MF∥AD.
∴四边形AMFD是平行四边形,
∴AM∥DF.
又DF平面EFDB,AM平面EFDB,∴AM∥平面EFDB.
同理可证,AN∥平面EFDB.
又AN,AM平面AMN,AM∩AN=A,∴平面AMN∥平面EFDB.
