1.5.2 平行关系的性质 同步练习1(含答案)
文档属性
| 名称 | 1.5.2 平行关系的性质 同步练习1(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 294.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览

文档简介
1.5.2
平行关系的性质
同步练习
一、选择题(每小题4分,共16分)
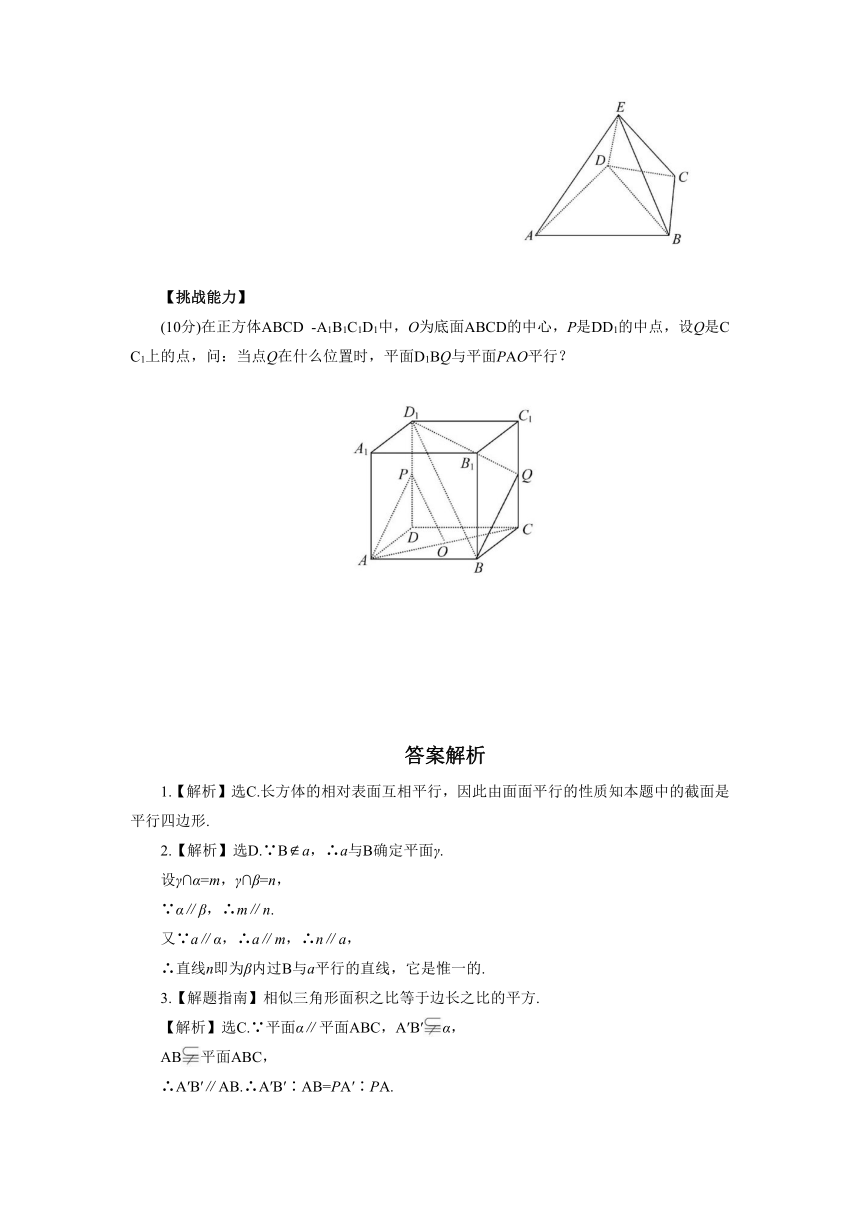
1.(易错题)如图给出的是长方体木料,想象沿图中平面所示位置截长方体,那么截面图形是下面四个图形的(
)
2.若平面α∥平面β,直线a∥α,且aβ,点B∈β,则在β内过点B的所有直线中(
)
(A)不一定存在与a平行的直线
(B)只有两条与a平行的直线
(C)存在无数条与a平行的直线
(D)存在惟一一条与a平行的直线
3.如图所示,P是三角形ABC所在平面外一点,
平面α∥平面ABC,α分别交线段PA,PB,PC于
A′,B′,C′.若PA′∶AA′=2∶5,求
△A′B′C′与△ABC的面积比为(
)
(A)2∶5
(B)2∶7
(C)4∶49
(D)9∶25
二、填空题(每小题4分,共8分)
4.
过正方体ABCD
-A1B1C1D1的顶点A1,C1,B的平面与底面ABCD所在平面的交线为l,则l与A1C1的位置关系是_________.
5.如图,直线a∥平面α,点A在α另一侧,
点B,C,D∈a,线段AB,AC,AD分别交α于
点E,F,G.若BD=4,CF=4,AF=5.则EG=_________.
三、解答题(每小题8分,共16分)
6.如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,
求证:DM∥平面BEC.
7.设平面α,β满足α∥β,A,C∈α,B,D∈β,直线AB与CD交于S,若SA=18,SB=9,CD=34.求SC的长度.
【挑战能力】
(10分)在正方体ABCD
-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?
答案解析
1.【解析】选C.长方体的相对表面互相平行,因此由面面平行的性质知本题中的截面是平行四边形.
2.【解析】选D.∵Ba,∴a与B确定平面γ.
设γ∩α=m,γ∩β=n,
∵α∥β,∴m∥n.
又∵a∥α,∴a∥m,∴n∥a,
∴直线n即为β内过B与a平行的直线,它是惟一的.
3.【解题指南】相似三角形面积之比等于边长之比的平方.
【解析】选C.∵平面α∥平面ABC,A′B′α,
AB平面ABC,
∴A′B′∥AB.∴A′B′∶AB=PA′∶PA.
又PA′∶AA′=2∶5,∴A′B′∶AB=2∶7.
同理B′C′∶BC=2∶7,A′C′∶AC=2∶7,
∴△A′B′C′∽△ABC,
∴S△A′B′C′∶S△ABC=4∶49.
4.【解题指南】用两个平面平行的性质去判断.
【解析】由于平面ABCD∥平面A1B1C1D1,平面A1B1C1D1∩平面A1C1B=A1C1,
平面ABCD∩平面A1C1B=l.由面面平行的性质可知l∥A1C1.
答案:平行
5.【解析】Aa,则点A与直线a确定一个平面,即平面ABD.
因为a∥α,且α∩平面ABD=EG,
故a∥EG,即BD∥EG.所以
答案:
6.【解题指南】(1)先取BD中点O,连接OC,OE,证明OE是BD的垂直平分线即可.
(2)本题考查线面的平行关系,可取AB中点N,连接MN,MD,DN,
利用平面MND∥平面BEC来证.
【证明】(1)设BD中点为O,连接OC,OE,
则由BC=CD知,CO⊥BD.
又已知CE⊥BD,CO∩CE=C,所以BD⊥平面OCE.
所以BD⊥OE,即OE是BD的垂直平分线,
所以BE=DE.
(2)取AB中点为N,连接MN,MD,DN,
∵M是AE的中点,∴MN∥BE.
∵△ABD是等边三角形,∴DN⊥AB.
由∠BCD=120°知,∠CBD=30°,
所以∠ABC=60°+30°=90°,即BC⊥AB,
所以ND∥BC,又因为MN∩DN=N,BE∩BC=B,所以平面MND∥平面BEC,
故DM∥平面BEC.
7.【解析】设相交直线AB,CD确定的平面为γ,
则α∩γ=AC,β∩γ=BD,
由α∥β,得AC∥BD.
S点在两平面同侧时,如图(1).
∵BD∥AC,所以
即∴SC=68.
S点在两平面之间时,如图(2).
∵BD∥AC,所以
即解得
综上知SC的长度为68或
【挑战能力】
【解析】如图,设平面D1BQ∩平面ADD1A1=D1M,
点M在AA1上,由于平面D1BQ∩平面BCC1B1=BQ,
平面ADD1A1∥平面BCC1B1,由面面平行的性质定理可得BQ∥D1M.
假设平面D1BQ∥平面PAO,
由平面D1BQ∩平面ADD1A1=D1M,
平面PAO∩平面ADD1A1=AP,
可得AP∥D1M,所以BQ∥D1M∥AP.
因为P为DD1的中点,所以M为AA1的中点,
所以Q为CC1的中点.
故当Q为CC1的中点时,平面D1BQ与平面PAO平行.
平行关系的性质
同步练习
一、选择题(每小题4分,共16分)
1.(易错题)如图给出的是长方体木料,想象沿图中平面所示位置截长方体,那么截面图形是下面四个图形的(
)
2.若平面α∥平面β,直线a∥α,且aβ,点B∈β,则在β内过点B的所有直线中(
)
(A)不一定存在与a平行的直线
(B)只有两条与a平行的直线
(C)存在无数条与a平行的直线
(D)存在惟一一条与a平行的直线
3.如图所示,P是三角形ABC所在平面外一点,
平面α∥平面ABC,α分别交线段PA,PB,PC于
A′,B′,C′.若PA′∶AA′=2∶5,求
△A′B′C′与△ABC的面积比为(
)
(A)2∶5
(B)2∶7
(C)4∶49
(D)9∶25
二、填空题(每小题4分,共8分)
4.
过正方体ABCD
-A1B1C1D1的顶点A1,C1,B的平面与底面ABCD所在平面的交线为l,则l与A1C1的位置关系是_________.
5.如图,直线a∥平面α,点A在α另一侧,
点B,C,D∈a,线段AB,AC,AD分别交α于
点E,F,G.若BD=4,CF=4,AF=5.则EG=_________.
三、解答题(每小题8分,共16分)
6.如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD.
(1)求证:BE=DE;
(2)若∠BCD=120°,M为线段AE的中点,
求证:DM∥平面BEC.
7.设平面α,β满足α∥β,A,C∈α,B,D∈β,直线AB与CD交于S,若SA=18,SB=9,CD=34.求SC的长度.
【挑战能力】
(10分)在正方体ABCD
-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?
答案解析
1.【解析】选C.长方体的相对表面互相平行,因此由面面平行的性质知本题中的截面是平行四边形.
2.【解析】选D.∵Ba,∴a与B确定平面γ.
设γ∩α=m,γ∩β=n,
∵α∥β,∴m∥n.
又∵a∥α,∴a∥m,∴n∥a,
∴直线n即为β内过B与a平行的直线,它是惟一的.
3.【解题指南】相似三角形面积之比等于边长之比的平方.
【解析】选C.∵平面α∥平面ABC,A′B′α,
AB平面ABC,
∴A′B′∥AB.∴A′B′∶AB=PA′∶PA.
又PA′∶AA′=2∶5,∴A′B′∶AB=2∶7.
同理B′C′∶BC=2∶7,A′C′∶AC=2∶7,
∴△A′B′C′∽△ABC,
∴S△A′B′C′∶S△ABC=4∶49.
4.【解题指南】用两个平面平行的性质去判断.
【解析】由于平面ABCD∥平面A1B1C1D1,平面A1B1C1D1∩平面A1C1B=A1C1,
平面ABCD∩平面A1C1B=l.由面面平行的性质可知l∥A1C1.
答案:平行
5.【解析】Aa,则点A与直线a确定一个平面,即平面ABD.
因为a∥α,且α∩平面ABD=EG,
故a∥EG,即BD∥EG.所以
答案:
6.【解题指南】(1)先取BD中点O,连接OC,OE,证明OE是BD的垂直平分线即可.
(2)本题考查线面的平行关系,可取AB中点N,连接MN,MD,DN,
利用平面MND∥平面BEC来证.
【证明】(1)设BD中点为O,连接OC,OE,
则由BC=CD知,CO⊥BD.
又已知CE⊥BD,CO∩CE=C,所以BD⊥平面OCE.
所以BD⊥OE,即OE是BD的垂直平分线,
所以BE=DE.
(2)取AB中点为N,连接MN,MD,DN,
∵M是AE的中点,∴MN∥BE.
∵△ABD是等边三角形,∴DN⊥AB.
由∠BCD=120°知,∠CBD=30°,
所以∠ABC=60°+30°=90°,即BC⊥AB,
所以ND∥BC,又因为MN∩DN=N,BE∩BC=B,所以平面MND∥平面BEC,
故DM∥平面BEC.
7.【解析】设相交直线AB,CD确定的平面为γ,
则α∩γ=AC,β∩γ=BD,
由α∥β,得AC∥BD.
S点在两平面同侧时,如图(1).
∵BD∥AC,所以
即∴SC=68.
S点在两平面之间时,如图(2).
∵BD∥AC,所以
即解得
综上知SC的长度为68或
【挑战能力】
【解析】如图,设平面D1BQ∩平面ADD1A1=D1M,
点M在AA1上,由于平面D1BQ∩平面BCC1B1=BQ,
平面ADD1A1∥平面BCC1B1,由面面平行的性质定理可得BQ∥D1M.
假设平面D1BQ∥平面PAO,
由平面D1BQ∩平面ADD1A1=D1M,
平面PAO∩平面ADD1A1=AP,
可得AP∥D1M,所以BQ∥D1M∥AP.
因为P为DD1的中点,所以M为AA1的中点,
所以Q为CC1的中点.
故当Q为CC1的中点时,平面D1BQ与平面PAO平行.
