1.5.2 平行关系的性质 同步练习2(含答案)
文档属性
| 名称 | 1.5.2 平行关系的性质 同步练习2(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 254.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 16:59:34 | ||
图片预览

文档简介
1.5.2
平行关系的性质同步练习
一、选择题(每小题4分,共16分)
1.下列说法中正确的是(
)
①若直线a∥b,b
平面α,则有a∥α;
②若直线a∥α,bα,则有a∥b;
③若直线a∥b,直线a∥α,则b∥α;
④若直线a∥α,b∥α,则a∥b.
(A)①④
(B)①③
(C)②
(D)均不正确
2.直线a∥平面α,α内有n条直线交于一点,则这n条直线中与直线a平行的直线有(
)
(A)0条
(B)
1条
(C)0或1条
(D)无数条
3.已知△ABC,△DBC分别在平面α,β内,E∈AB,
F∈AC,M∈DB,N∈DC,且EF∥MN,则EF与BC的位置关系是(
)
(A)平行
(B)相交或平行
(C)平行或异面
(D)平行、相交或异面
4.(易错题)如图,四棱锥S-ABCD的所有的
棱长都等于2,E是SA的中点,过C,D,E三点的
平面与SB交于点F,则四边形DEFC的周长为(
)
(A)2+
(B)3+
(C)3+
(D)2+
二、填空题(每小题4分,共8分)
5.一个面截空间四边形的四边得到四个交点,如果该空间四边形的两条对角线与这个截面平行,那么此四个交点围成的四边形是
________.
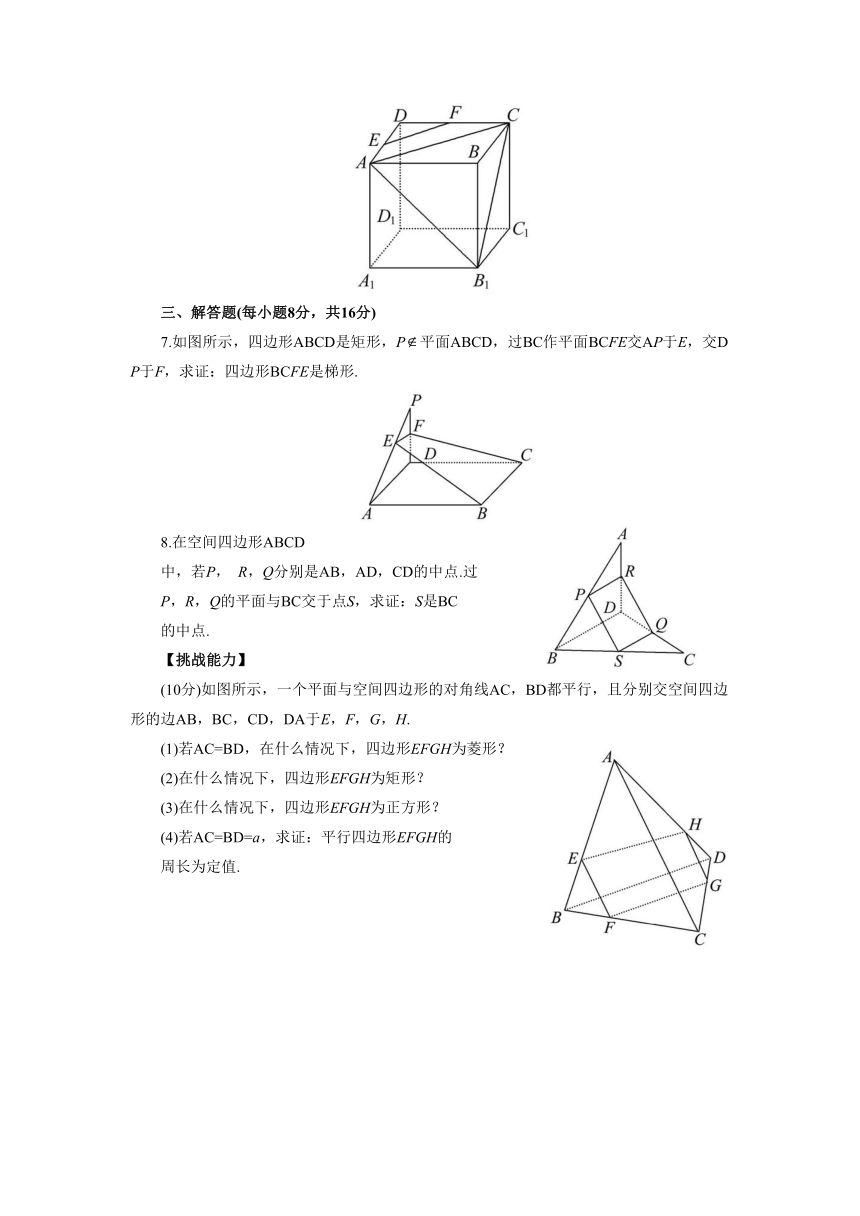
6.如图,正方体ABCD
-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于_________.
三、解答题(每小题8分,共16分)
7.如图所示,四边形ABCD是矩形,P平面ABCD,过BC作平面BCFE交AP于E,交DP于F,求证:四边形BCFE是梯形.
8.在空间四边形ABCD
中,若P,
R,Q分别是AB,AD,CD的中点.过
P,R,Q的平面与BC交于点S,求证:S是BC
的中点.
【挑战能力】
(10分)如图所示,一个平面与空间四边形的对角线AC,BD都平行,且分别交空间四边形的边AB,BC,CD,DA于E,F,G,H.
(1)若AC=BD,在什么情况下,四边形EFGH为菱形?
(2)在什么情况下,四边形EFGH为矩形?
(3)在什么情况下,四边形EFGH为正方形?
(4)若AC=BD=a,求证:平行四边形EFGH的
周长为定值.
答案解析
1.【解析】选D.①中可能aα或a∥α,②a与b可能异面,③中b可能在平面α内,④a与b可能相交、平行或异面.
2.【解析】选C.过直线a与交点作平面β,设平面β与α交于直线b,则a∥b,若所给n条直线中有1条是与b重合的,则此直线与直线a平行,若没有与b重合的,则与直线a平行的直线有0条.
3.【解析】选A.EF∥MN,MNβ,EFβ,
∴EF∥β.又EFα,α∩β=BC,
∴EF∥BC.
4.【解题指南】先证明EF∥AB,再根据三角形中位线等知识求解.
【解析】选C.∵AB=BC=CD=AD=2,
∴四边形ABCD为菱形,∴CD∥AB.
又CD平面SAB,AB平面SAB,
∴CD∥平面SAB.
又CD平面CDEF,
平面CDEF∩平面SAB=EF,
∴CD∥EF,∴EF∥AB.
又∵E为SA的中点,∴EF=AB=1,
又∵△SAD和△SBC都是等边三角形,
∴DE=CF=2×sin60°=
∴四边形DEFC的周长为:DE+EF+CF+CD=+1++2=3+
5.【解析】由线面平行的性质定理知,该四边形的两组对边分别平行,故该四边形为平行四边形.
答案:平行四边形
6.【解析】∵EF∥平面AB1C,EF平面ADC,
平面ADC∩平面AB1C=AC,
由线面平行的性质定理,得EF∥AC.
又∵E为AD的中点,
∴F为CD的中点,即EF为△ADC的中位线,
∴EF=AC.又正方体的棱长为2,
∴AC=,∴EF=AC=×=.
答案:
7.【证明】∵四边形ABCD为矩形,
∴BC∥AD.
∵AD平面PAD,BC平面PAD,
∴BC∥平面PAD.
∵平面BCFE∩平面PAD=EF,
∴BC∥EF.
∵AD=BC,AD≠EF,
∴BC≠EF,
∴四边形BCFE为梯形.
【误区警示】要证一个四边形是梯形,除了要证明一组对边平行外,还应证明它们的长度不相等.
【方法技巧】立体几何证明题的做题思路
立体几何证明题往往从以下三个方面思考
(1)从题目的结论出发去选择相应的证明方法并进行“逆向思维”.
(2)当逆推出现困难时,可根据已知条件联想或推导出有关的性质,使题设和结论逐步靠近.
(3)及时进行条件与结论之间的联系和沟通,找到证明思路.
这种“两头凑”的方法其实是解决数学问题的常用思维方法.
8.【解题指南】由于Q是CD的中点,要证S是BC的中点只需证SQ∥BD.
【证明】在△ABD中,点P、R分别是AB、AD的中点,则PR∥BD.
又PR平面BCD,BD平面BCD.
∴PR∥平面BCD.
又PR平面PRQS,平面PRQS∩平面BCD=SQ.
故PR∥SQ,又PR∥BD,
∴SQ∥BD,
又Q是CD的中点,∴S是BC的中点.
【挑战能力】
【解析】(1)∵AC∥平面EFGH,且AC平面ABC,平面ABC∩平面EFGH=EF,
∴AC∥EF.
同理AC∥GH.
∴EF∥GH,
同理EH∥FG,
∴四边形EFGH为平行四边形.
在△ABD中,
在△ADC中,
∵AC=BD,∴若使四边形EFGH为菱形.
只需EH=HG,即只需AH=DH.
∴当H为AD中点时,四边形EFGH为菱形.
同理当E、F、G分别为对应边中点时,四边形EFGH为菱形.
(2)∵EH∥BD,GH∥AC,
∴当BD⊥AC时,EH⊥GH.
此时四边形EFGH为矩形.
(3)在(1)、(2)的条件下,即AC=BD,BD⊥AC,且H为AD的中点时,四边形EFGH为正方形.
(4)∵
①
②
①+②,得∴EH+GH=a.
∴平行四边形EFGH的周长为定值2a.
平行关系的性质同步练习
一、选择题(每小题4分,共16分)
1.下列说法中正确的是(
)
①若直线a∥b,b
平面α,则有a∥α;
②若直线a∥α,bα,则有a∥b;
③若直线a∥b,直线a∥α,则b∥α;
④若直线a∥α,b∥α,则a∥b.
(A)①④
(B)①③
(C)②
(D)均不正确
2.直线a∥平面α,α内有n条直线交于一点,则这n条直线中与直线a平行的直线有(
)
(A)0条
(B)
1条
(C)0或1条
(D)无数条
3.已知△ABC,△DBC分别在平面α,β内,E∈AB,
F∈AC,M∈DB,N∈DC,且EF∥MN,则EF与BC的位置关系是(
)
(A)平行
(B)相交或平行
(C)平行或异面
(D)平行、相交或异面
4.(易错题)如图,四棱锥S-ABCD的所有的
棱长都等于2,E是SA的中点,过C,D,E三点的
平面与SB交于点F,则四边形DEFC的周长为(
)
(A)2+
(B)3+
(C)3+
(D)2+
二、填空题(每小题4分,共8分)
5.一个面截空间四边形的四边得到四个交点,如果该空间四边形的两条对角线与这个截面平行,那么此四个交点围成的四边形是
________.
6.如图,正方体ABCD
-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于_________.
三、解答题(每小题8分,共16分)
7.如图所示,四边形ABCD是矩形,P平面ABCD,过BC作平面BCFE交AP于E,交DP于F,求证:四边形BCFE是梯形.
8.在空间四边形ABCD
中,若P,
R,Q分别是AB,AD,CD的中点.过
P,R,Q的平面与BC交于点S,求证:S是BC
的中点.
【挑战能力】
(10分)如图所示,一个平面与空间四边形的对角线AC,BD都平行,且分别交空间四边形的边AB,BC,CD,DA于E,F,G,H.
(1)若AC=BD,在什么情况下,四边形EFGH为菱形?
(2)在什么情况下,四边形EFGH为矩形?
(3)在什么情况下,四边形EFGH为正方形?
(4)若AC=BD=a,求证:平行四边形EFGH的
周长为定值.
答案解析
1.【解析】选D.①中可能aα或a∥α,②a与b可能异面,③中b可能在平面α内,④a与b可能相交、平行或异面.
2.【解析】选C.过直线a与交点作平面β,设平面β与α交于直线b,则a∥b,若所给n条直线中有1条是与b重合的,则此直线与直线a平行,若没有与b重合的,则与直线a平行的直线有0条.
3.【解析】选A.EF∥MN,MNβ,EFβ,
∴EF∥β.又EFα,α∩β=BC,
∴EF∥BC.
4.【解题指南】先证明EF∥AB,再根据三角形中位线等知识求解.
【解析】选C.∵AB=BC=CD=AD=2,
∴四边形ABCD为菱形,∴CD∥AB.
又CD平面SAB,AB平面SAB,
∴CD∥平面SAB.
又CD平面CDEF,
平面CDEF∩平面SAB=EF,
∴CD∥EF,∴EF∥AB.
又∵E为SA的中点,∴EF=AB=1,
又∵△SAD和△SBC都是等边三角形,
∴DE=CF=2×sin60°=
∴四边形DEFC的周长为:DE+EF+CF+CD=+1++2=3+
5.【解析】由线面平行的性质定理知,该四边形的两组对边分别平行,故该四边形为平行四边形.
答案:平行四边形
6.【解析】∵EF∥平面AB1C,EF平面ADC,
平面ADC∩平面AB1C=AC,
由线面平行的性质定理,得EF∥AC.
又∵E为AD的中点,
∴F为CD的中点,即EF为△ADC的中位线,
∴EF=AC.又正方体的棱长为2,
∴AC=,∴EF=AC=×=.
答案:
7.【证明】∵四边形ABCD为矩形,
∴BC∥AD.
∵AD平面PAD,BC平面PAD,
∴BC∥平面PAD.
∵平面BCFE∩平面PAD=EF,
∴BC∥EF.
∵AD=BC,AD≠EF,
∴BC≠EF,
∴四边形BCFE为梯形.
【误区警示】要证一个四边形是梯形,除了要证明一组对边平行外,还应证明它们的长度不相等.
【方法技巧】立体几何证明题的做题思路
立体几何证明题往往从以下三个方面思考
(1)从题目的结论出发去选择相应的证明方法并进行“逆向思维”.
(2)当逆推出现困难时,可根据已知条件联想或推导出有关的性质,使题设和结论逐步靠近.
(3)及时进行条件与结论之间的联系和沟通,找到证明思路.
这种“两头凑”的方法其实是解决数学问题的常用思维方法.
8.【解题指南】由于Q是CD的中点,要证S是BC的中点只需证SQ∥BD.
【证明】在△ABD中,点P、R分别是AB、AD的中点,则PR∥BD.
又PR平面BCD,BD平面BCD.
∴PR∥平面BCD.
又PR平面PRQS,平面PRQS∩平面BCD=SQ.
故PR∥SQ,又PR∥BD,
∴SQ∥BD,
又Q是CD的中点,∴S是BC的中点.
【挑战能力】
【解析】(1)∵AC∥平面EFGH,且AC平面ABC,平面ABC∩平面EFGH=EF,
∴AC∥EF.
同理AC∥GH.
∴EF∥GH,
同理EH∥FG,
∴四边形EFGH为平行四边形.
在△ABD中,
在△ADC中,
∵AC=BD,∴若使四边形EFGH为菱形.
只需EH=HG,即只需AH=DH.
∴当H为AD中点时,四边形EFGH为菱形.
同理当E、F、G分别为对应边中点时,四边形EFGH为菱形.
(2)∵EH∥BD,GH∥AC,
∴当BD⊥AC时,EH⊥GH.
此时四边形EFGH为矩形.
(3)在(1)、(2)的条件下,即AC=BD,BD⊥AC,且H为AD的中点时,四边形EFGH为正方形.
(4)∵
①
②
①+②,得∴EH+GH=a.
∴平行四边形EFGH的周长为定值2a.
