1.6.1 垂直关系的判定 同步练习2(含答案)
文档属性
| 名称 | 1.6.1 垂直关系的判定 同步练习2(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 17:07:57 | ||
图片预览

文档简介
1.6.1
垂直关系的判定
同步练习
课后训练
1.若三条直线OA,OB,
OC两两垂直,则直线OA垂直于( ).
A.平面OAB
B.平面OAC
C.平面OBC
D.平面ABC
2.一条直线和三角形的两边同时垂直,则这条直线和三角形的第三边的位置关系是( ).
A.平行
B.垂直
C.相交不垂直
D.不确定
3.下列结论正确的是( ).
A.若直线a∥平面α,直线b⊥a,b平面β,则α⊥β
B.若直线a⊥直线b,a⊥平面α,b⊥平面β,则α⊥β
C.过平面外的一条直线有且只有一个平面与已知平面垂直
D.过平面外一点有且只有一个平面与已知平面垂直
4.如图,在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1内运动,并且总保持AP⊥BD1,则动点P在( ).
A.线段B1C上
B.线段BC1上
C.BB1中点与CC1中点的连线上
D.B1C1中点与BC中点的连线上
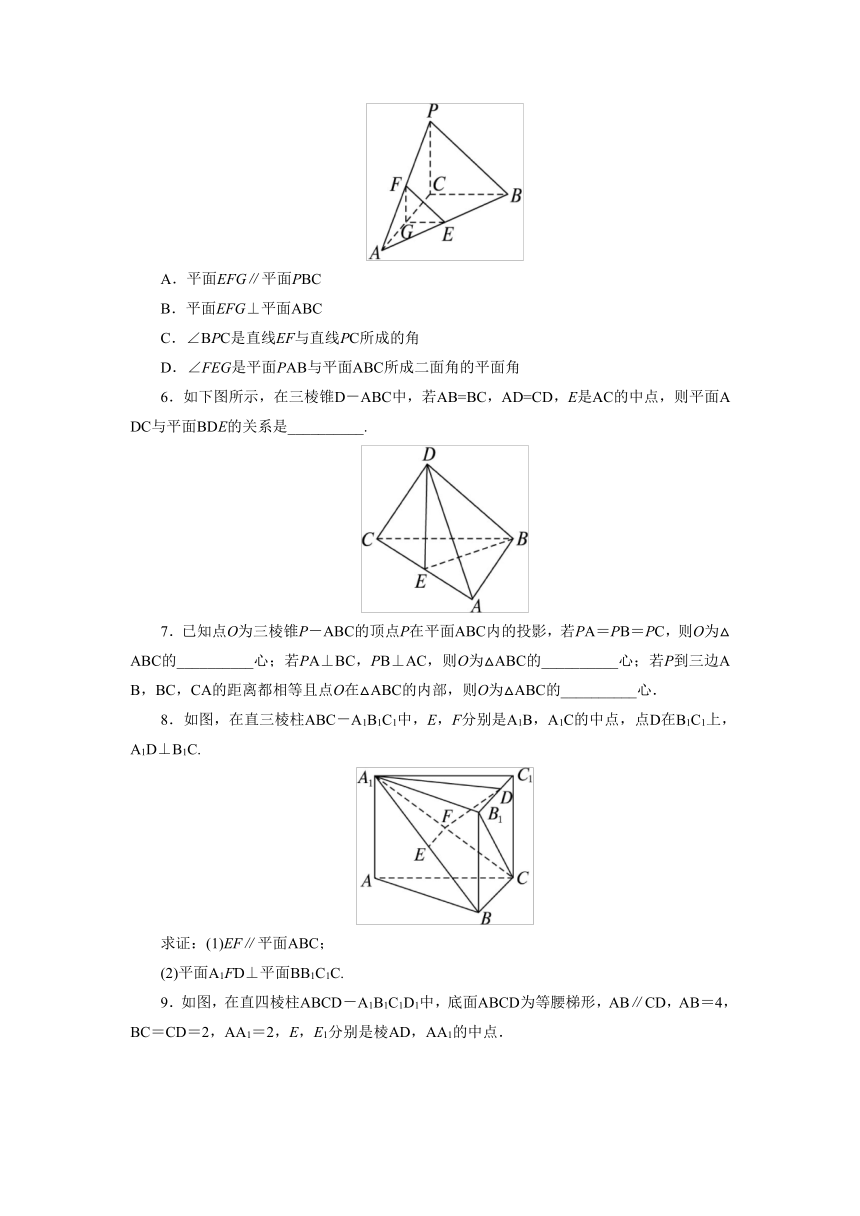
5.如图,在三棱锥P-ABC中,已知PC⊥BC,PC⊥AC,点E,F,G分别是所在棱的中点,则下面结论中错误的是( ).
A.平面EFG∥平面PBC
B.平面EFG⊥平面ABC
C.∠BPC是直线EF与直线PC所成的角
D.∠FEG是平面PAB与平面ABC所成二面角的平面角
6.如下图所示,在三棱锥D-ABC中,若AB=BC,AD=CD,E是AC的中点,则平面ADC与平面BDE的关系是__________.
7.已知点O为三棱锥P-ABC的顶点P在平面ABC内的投影,若PA=PB=PC,则O为△ABC的__________心;若PA⊥BC,PB⊥AC,则O为△ABC的__________心;若P到三边AB,BC,CA的距离都相等且点O在△ABC的内部,则O为△ABC的__________心.
8.如图,在直三棱柱ABC-A1B1C1中,E,F分别是A1B,A1C的中点,点D在B1C1上,A1D⊥B1C.
求证:(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
9.如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
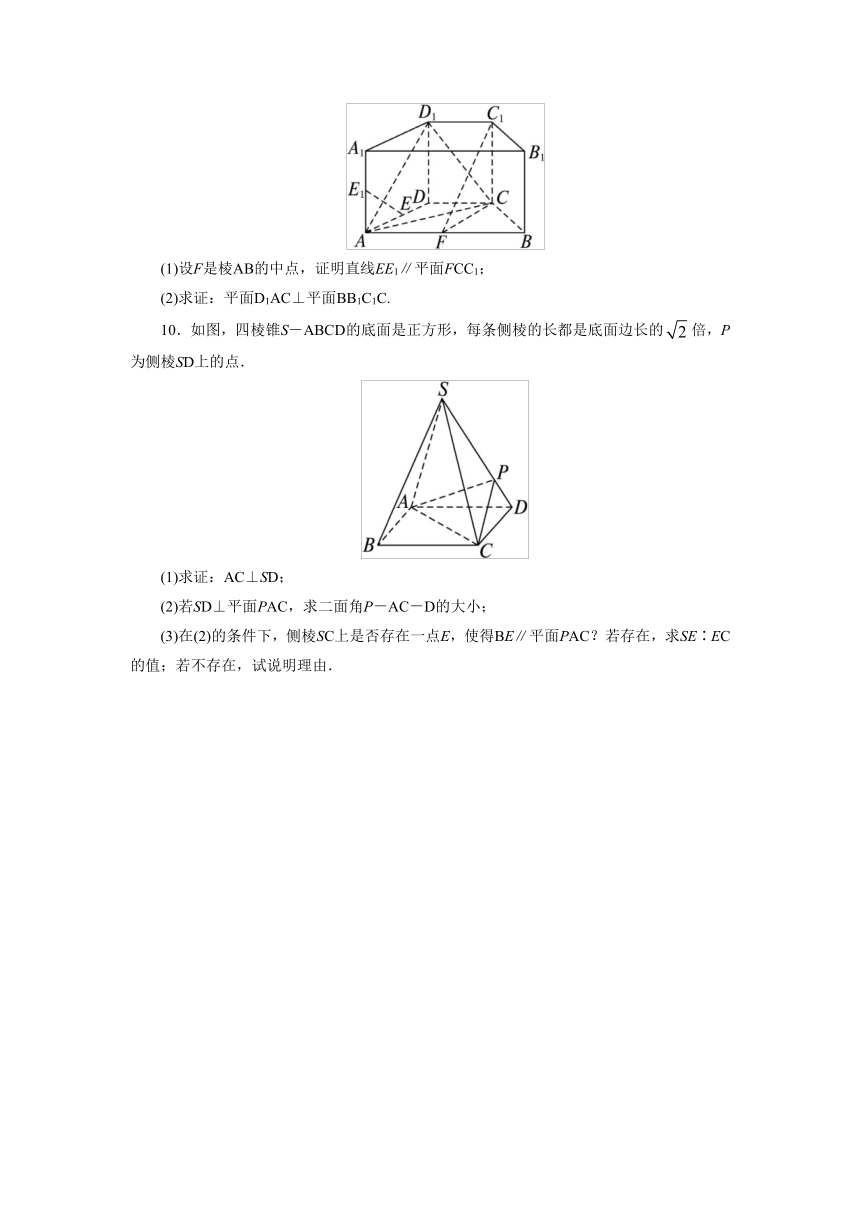
(1)设F是棱AB的中点,证明直线EE1∥平面FCC1;
(2)求证:平面D1AC⊥平面BB1C1C.
10.如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点.
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P-AC-D的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
参考答案
1答案:C 解析:由于OA⊥OB,OA⊥OC,且OB∩OC=O,
所以OA⊥平面OBC.
2答案:B
3答案:B
4答案:A 解析:易知BD1⊥平面AB1C,故P∈B1C.
5答案:D 解析:由已知PC⊥BC,PC⊥AC,
又AC∩BC=C,
∴PC⊥平面ABC.
又FG∥PC,
∴FG⊥平面ABC.
又FG平面EFG,
∴平面EFG⊥平面ABC,
故B正确.
∵FG∥PC,GE∥BC,
∴平面EFG∥平面PBC.
故A正确.
由异面直线所成角的定义知C正确.故选D.
6答案:垂直 解析:易知BE⊥AC,DE⊥AC,∴AC⊥平面BDE.
又AC平面ADC,
∴平面ADC⊥平面BDE.
7答案:外 垂 内 解析:连接OA,OB,OC,由PA=PB=PC,
∴OA=OB=OC,O是△ABC的外心.
若PA⊥BC,又PO⊥平面ABC,∴BC⊥PO.
∴BC⊥平面PAO.∴BC⊥AO.
同理AC⊥OB.
∴O是△ABC的垂心.
若P到AB,BC边的距离相等,则易知O到AB,BC边的距离也相等,从而可判定O是△ABC的内心.
8答案:证明:(1)因为E,F分别是A1B,A1C的中点,21世纪教育网
所以EF∥BC,又EF平面ABC,BC平面ABC,
所以EF∥平面ABC.
(2)因为三棱柱ABC-A1B1C1是直三棱柱,所以BB1⊥平面A1B1C1,BB1⊥A1D,
又A1D⊥B1C,BB1∩B1C=B1,
所以A1D⊥平面BB1C1C,
又A1D平面A1FD,所以平面A1FD⊥平面BB1C1C.
9答案:证明:(1)在直四棱柱ABCD-A1B1C1D1中,
取A1B1的中点F1,连接A1D,C1F1,CF1,
因为AB=4,CD=2,且AB∥CD,所以CD=A1F1,CD∥A1F1,四边形A1F1CD为平行四边形,
所以CF1∥A1D.又因为E,E1分别是棱AD,AA1的中点,所以EE1∥A1D,所以CF1∥EE1.
又因为EE1平面FCC1,CF1平面FCC1,
所以直线EE1∥平面FCC1.
(2)在直棱柱中,CC1⊥平面ABCD,AC平面ABCD,所以CC1⊥AC.
因为底面ABCD为等腰梯形,AB=4,BC=2,F是棱AB的中点,所以CF=CB=BF,△BCF为正三角形,∠BCF=60°,△ACF为等腰三角形,且∠ACF=30°,
所以AC⊥BC.
又因为BC与CC1都在平面BB1C1C内且交于点C,
所以AC⊥平面BB1C1C,而AC平面D1AC,
所以平面D1AC⊥平面BB1C1C.
10答案:(1)证明:连接BD,设AC交BD于O,连接SO.由题意知SO⊥AC.在正方形ABCD中,AC⊥BD,所以AC⊥平面SBD,得AC⊥SD.
(2)解:设正方形边长为a,则SD=a,又OD=a,所以∠SDO=60°.连接OP,由(1)知AC⊥平面SBD,所以AC⊥OP,且AC⊥OD,所以∠POD是二面角P-AC-D的平面角.由SD⊥平面PAC,知SD⊥OP,
所以∠POD=30°,即二面角P-AC-D的大小为30°.
(3)解:在棱SC上存在一点E,使BE∥平面PAC.
由(2)可得PD=a,故可在SP上取一点N,使PN=PD.过N作PC的平行线与SC的交点即为E.连接BN,在△BDN中,知BN∥PO.又由于NE∥PC,故平面BEN∥平面PAC,可得BE∥平面PAC.由于SN∶NP=2∶1,故SE∶EC=2∶1.
垂直关系的判定
同步练习
课后训练
1.若三条直线OA,OB,
OC两两垂直,则直线OA垂直于( ).
A.平面OAB
B.平面OAC
C.平面OBC
D.平面ABC
2.一条直线和三角形的两边同时垂直,则这条直线和三角形的第三边的位置关系是( ).
A.平行
B.垂直
C.相交不垂直
D.不确定
3.下列结论正确的是( ).
A.若直线a∥平面α,直线b⊥a,b平面β,则α⊥β
B.若直线a⊥直线b,a⊥平面α,b⊥平面β,则α⊥β
C.过平面外的一条直线有且只有一个平面与已知平面垂直
D.过平面外一点有且只有一个平面与已知平面垂直
4.如图,在正方体ABCD-A1B1C1D1中,点P在侧面BCC1B1内运动,并且总保持AP⊥BD1,则动点P在( ).
A.线段B1C上
B.线段BC1上
C.BB1中点与CC1中点的连线上
D.B1C1中点与BC中点的连线上
5.如图,在三棱锥P-ABC中,已知PC⊥BC,PC⊥AC,点E,F,G分别是所在棱的中点,则下面结论中错误的是( ).
A.平面EFG∥平面PBC
B.平面EFG⊥平面ABC
C.∠BPC是直线EF与直线PC所成的角
D.∠FEG是平面PAB与平面ABC所成二面角的平面角
6.如下图所示,在三棱锥D-ABC中,若AB=BC,AD=CD,E是AC的中点,则平面ADC与平面BDE的关系是__________.
7.已知点O为三棱锥P-ABC的顶点P在平面ABC内的投影,若PA=PB=PC,则O为△ABC的__________心;若PA⊥BC,PB⊥AC,则O为△ABC的__________心;若P到三边AB,BC,CA的距离都相等且点O在△ABC的内部,则O为△ABC的__________心.
8.如图,在直三棱柱ABC-A1B1C1中,E,F分别是A1B,A1C的中点,点D在B1C1上,A1D⊥B1C.
求证:(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
9.如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.
(1)设F是棱AB的中点,证明直线EE1∥平面FCC1;
(2)求证:平面D1AC⊥平面BB1C1C.
10.如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的倍,P为侧棱SD上的点.
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P-AC-D的大小;
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC?若存在,求SE∶EC的值;若不存在,试说明理由.
参考答案
1答案:C 解析:由于OA⊥OB,OA⊥OC,且OB∩OC=O,
所以OA⊥平面OBC.
2答案:B
3答案:B
4答案:A 解析:易知BD1⊥平面AB1C,故P∈B1C.
5答案:D 解析:由已知PC⊥BC,PC⊥AC,
又AC∩BC=C,
∴PC⊥平面ABC.
又FG∥PC,
∴FG⊥平面ABC.
又FG平面EFG,
∴平面EFG⊥平面ABC,
故B正确.
∵FG∥PC,GE∥BC,
∴平面EFG∥平面PBC.
故A正确.
由异面直线所成角的定义知C正确.故选D.
6答案:垂直 解析:易知BE⊥AC,DE⊥AC,∴AC⊥平面BDE.
又AC平面ADC,
∴平面ADC⊥平面BDE.
7答案:外 垂 内 解析:连接OA,OB,OC,由PA=PB=PC,
∴OA=OB=OC,O是△ABC的外心.
若PA⊥BC,又PO⊥平面ABC,∴BC⊥PO.
∴BC⊥平面PAO.∴BC⊥AO.
同理AC⊥OB.
∴O是△ABC的垂心.
若P到AB,BC边的距离相等,则易知O到AB,BC边的距离也相等,从而可判定O是△ABC的内心.
8答案:证明:(1)因为E,F分别是A1B,A1C的中点,21世纪教育网
所以EF∥BC,又EF平面ABC,BC平面ABC,
所以EF∥平面ABC.
(2)因为三棱柱ABC-A1B1C1是直三棱柱,所以BB1⊥平面A1B1C1,BB1⊥A1D,
又A1D⊥B1C,BB1∩B1C=B1,
所以A1D⊥平面BB1C1C,
又A1D平面A1FD,所以平面A1FD⊥平面BB1C1C.
9答案:证明:(1)在直四棱柱ABCD-A1B1C1D1中,
取A1B1的中点F1,连接A1D,C1F1,CF1,
因为AB=4,CD=2,且AB∥CD,所以CD=A1F1,CD∥A1F1,四边形A1F1CD为平行四边形,
所以CF1∥A1D.又因为E,E1分别是棱AD,AA1的中点,所以EE1∥A1D,所以CF1∥EE1.
又因为EE1平面FCC1,CF1平面FCC1,
所以直线EE1∥平面FCC1.
(2)在直棱柱中,CC1⊥平面ABCD,AC平面ABCD,所以CC1⊥AC.
因为底面ABCD为等腰梯形,AB=4,BC=2,F是棱AB的中点,所以CF=CB=BF,△BCF为正三角形,∠BCF=60°,△ACF为等腰三角形,且∠ACF=30°,
所以AC⊥BC.
又因为BC与CC1都在平面BB1C1C内且交于点C,
所以AC⊥平面BB1C1C,而AC平面D1AC,
所以平面D1AC⊥平面BB1C1C.
10答案:(1)证明:连接BD,设AC交BD于O,连接SO.由题意知SO⊥AC.在正方形ABCD中,AC⊥BD,所以AC⊥平面SBD,得AC⊥SD.
(2)解:设正方形边长为a,则SD=a,又OD=a,所以∠SDO=60°.连接OP,由(1)知AC⊥平面SBD,所以AC⊥OP,且AC⊥OD,所以∠POD是二面角P-AC-D的平面角.由SD⊥平面PAC,知SD⊥OP,
所以∠POD=30°,即二面角P-AC-D的大小为30°.
(3)解:在棱SC上存在一点E,使BE∥平面PAC.
由(2)可得PD=a,故可在SP上取一点N,使PN=PD.过N作PC的平行线与SC的交点即为E.连接BN,在△BDN中,知BN∥PO.又由于NE∥PC,故平面BEN∥平面PAC,可得BE∥平面PAC.由于SN∶NP=2∶1,故SE∶EC=2∶1.
