1.7.1 简单几何体的侧面积 同步练习1(含答案)
文档属性
| 名称 | 1.7.1 简单几何体的侧面积 同步练习1(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览

文档简介
1.7.1
简单几何体的侧面积
同步练习
课后训练
1.轴截面为正方形的圆柱的侧面积与表面积的比是( ).
A.1∶2
B.2∶3
C.1∶3
D.1∶4
2.侧面都是直角三角形的正三棱锥,底面边长为a,则该三棱锥的表面积是( ).
A.
B.
C.
D.
3.一个圆台的母线长等于上、下底面半径和的一半,且侧面积是32π,则母线长为( ).
A.2
B.
C.4
D.8
4.某四棱锥的三视图如图所示,该四棱锥的表面积是( ).
A.32
B.
C.48
D.
5.圆台的上、下底面半径和高的比为1∶4∶4,母线长为10,则圆台的侧面积为( ).
A.81π
B.100π
C.14π
D.169π
6.正四棱台的上、下两底面边长分别是方程x2-9x+18=0的两根,其侧面积等于两底面积之和,则其侧面梯形的高为__________.
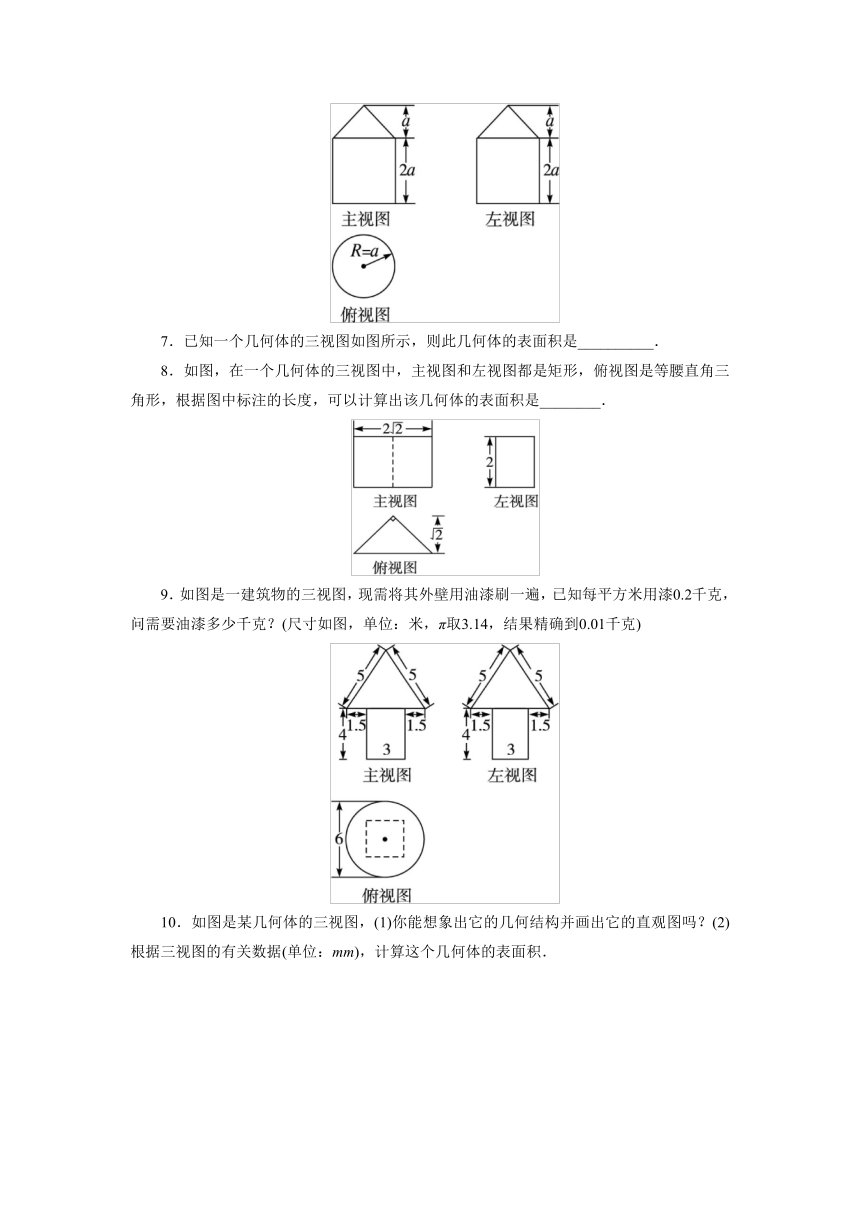
7.已知一个几何体的三视图如图所示,则此几何体的表面积是__________.
8.如图,在一个几何体的三视图中,主视图和左视图都是矩形,俯视图是等腰直角三角形,根据图中标注的长度,可以计算出该几何体的表面积是________.
9.如图是一建筑物的三视图,现需将其外壁用油漆刷一遍,已知每平方米用漆0.2千克,问需要油漆多少千克?(尺寸如图,单位:米,π取3.14,结果精确到0.01千克)
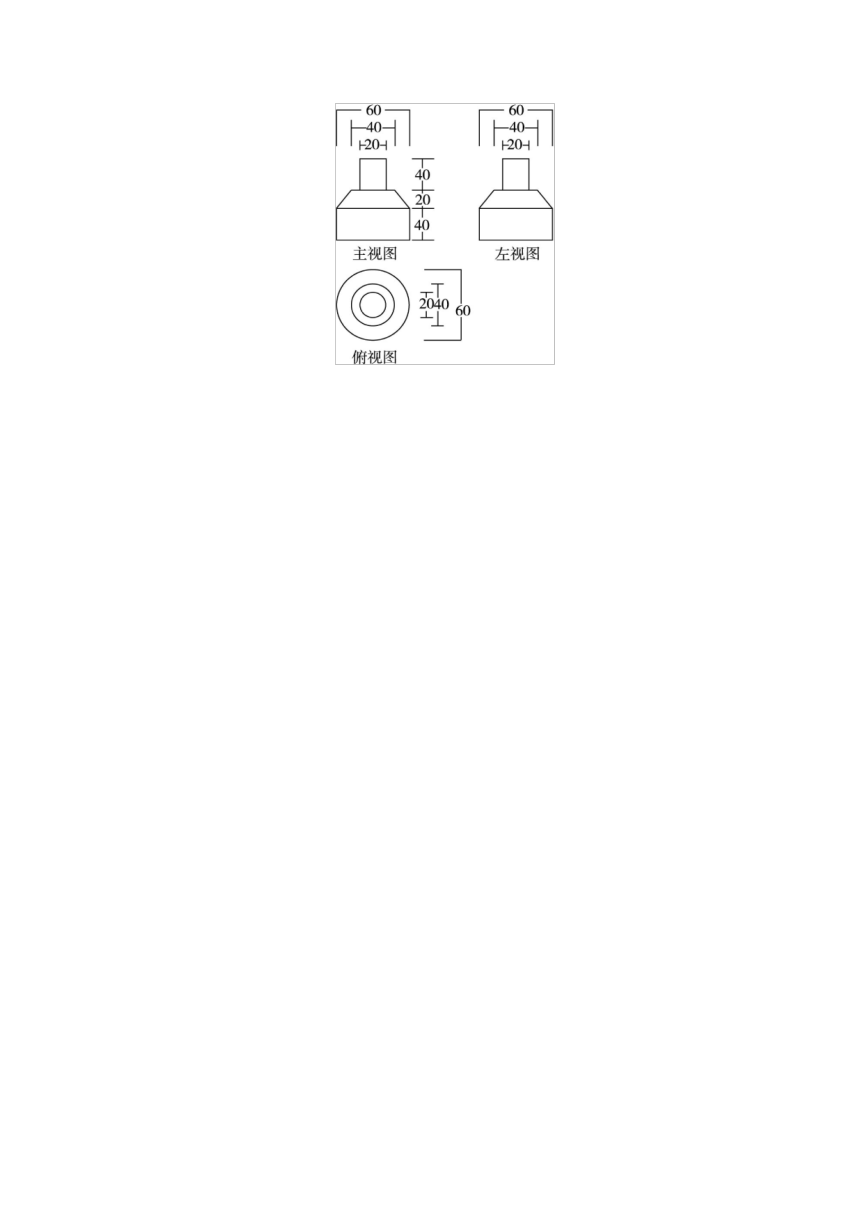
10.如图是某几何体的三视图,(1)你能想象出它的几何结构并画出它的直观图吗?(2)根据三视图的有关数据(单位:mm),计算这个几何体的表面积.
参考答案
1答案:B 解析:设圆柱的底面半径为r,母线长为l,依题意得l=2r,而S侧面积=2πrl,S表面积=2πr2+2πrl,∴S侧面积∶S表面积=2πrl∶(2πr2+2πrl)=2∶3,故选B.
2答案:A 解析:因为底面边长为a,则斜高为,
故.
而,故.
3答案:C 解析:设圆台的母线长为l,上、下底面半径分别为r,R,
则l=(r+R),
又32π=π(r+R)l=2πl2,
∴l2=16,∴l=4.
4答案:B 解析:由三视图知原几何体是一个底面边长为4,高是2的正四棱锥.如图:
∵AO=2,OB=2,
∴AB=.
又∵S侧=4××4×=,S底=4×4=16,
∴S表=S侧+S底=16+.
5答案:B 解析:设上底面半径为r,则下底面半径为4r,高为4r,于是可得母线长为=5r,依题意,5r=10,∴r=2.因此圆台侧面积S=π(2+8)×10=100π.
6答案: 解析:方程x2-9x+18=0的两个根为x1=3,x2=6,
设侧面梯形的高为h,则由题意得×(3+6)·h×4=32+62,h=.
7答案:(5+)πa2 解析:S圆锥侧=π×a×=πa2,
S圆柱侧=2π×a×2a=4πa2,S底面=πa2,
∴S表=S圆锥侧+S圆柱侧+S底面
=5πa2+πa2=(5+)πa2.
8答案: 解析:如图,该几何体为底面为等腰直角三角形的直棱柱.由图知AB=AC,BC=,AB⊥AC.
∴S表=+2×2×2+2×=12+.
9答案:解:建筑物为一组合体,上面是底面半径为3米,母线长为5米的圆锥,下面是底面边长为3米,高为4米的正四棱柱.
圆锥的表面积=πr2+πrl
≈3.14×32+3.14×3×5
=28.26+47.1=75.36.
四棱柱的一个底面积=32=9,
四棱柱的侧面积=4×4×3=48.
所以外壁面积S≈75.36-9+48=114.36(平方米).
故需油漆114.36×0.2=22.872≈22.88(千克).
答:共需约22.88千克油漆.
10答案:解:(1)由三视图可知这个几何体是由两个圆柱夹一个圆台组成的,其中下面圆柱底面直径为60
mm,母线长40
mm,中间圆台上、下底直径分别为40
mm,60
mm,高为20
mm,上面圆柱的底面直径为20
mm,高为40
mm,其直观图如图所示.
(2)由三视图可知圆台母线长
(mm).
∴所求的表面积S=S下圆柱下底+S下圆柱侧+S圆台侧+(S圆台上底-S上圆柱下底)+S上圆柱侧+S上圆柱上底
=
=900π+2
400π+π+400π+800π
=(4
500π+π)(mm2)
=(45π+π)(cm2).
简单几何体的侧面积
同步练习
课后训练
1.轴截面为正方形的圆柱的侧面积与表面积的比是( ).
A.1∶2
B.2∶3
C.1∶3
D.1∶4
2.侧面都是直角三角形的正三棱锥,底面边长为a,则该三棱锥的表面积是( ).
A.
B.
C.
D.
3.一个圆台的母线长等于上、下底面半径和的一半,且侧面积是32π,则母线长为( ).
A.2
B.
C.4
D.8
4.某四棱锥的三视图如图所示,该四棱锥的表面积是( ).
A.32
B.
C.48
D.
5.圆台的上、下底面半径和高的比为1∶4∶4,母线长为10,则圆台的侧面积为( ).
A.81π
B.100π
C.14π
D.169π
6.正四棱台的上、下两底面边长分别是方程x2-9x+18=0的两根,其侧面积等于两底面积之和,则其侧面梯形的高为__________.
7.已知一个几何体的三视图如图所示,则此几何体的表面积是__________.
8.如图,在一个几何体的三视图中,主视图和左视图都是矩形,俯视图是等腰直角三角形,根据图中标注的长度,可以计算出该几何体的表面积是________.
9.如图是一建筑物的三视图,现需将其外壁用油漆刷一遍,已知每平方米用漆0.2千克,问需要油漆多少千克?(尺寸如图,单位:米,π取3.14,结果精确到0.01千克)
10.如图是某几何体的三视图,(1)你能想象出它的几何结构并画出它的直观图吗?(2)根据三视图的有关数据(单位:mm),计算这个几何体的表面积.
参考答案
1答案:B 解析:设圆柱的底面半径为r,母线长为l,依题意得l=2r,而S侧面积=2πrl,S表面积=2πr2+2πrl,∴S侧面积∶S表面积=2πrl∶(2πr2+2πrl)=2∶3,故选B.
2答案:A 解析:因为底面边长为a,则斜高为,
故.
而,故.
3答案:C 解析:设圆台的母线长为l,上、下底面半径分别为r,R,
则l=(r+R),
又32π=π(r+R)l=2πl2,
∴l2=16,∴l=4.
4答案:B 解析:由三视图知原几何体是一个底面边长为4,高是2的正四棱锥.如图:
∵AO=2,OB=2,
∴AB=.
又∵S侧=4××4×=,S底=4×4=16,
∴S表=S侧+S底=16+.
5答案:B 解析:设上底面半径为r,则下底面半径为4r,高为4r,于是可得母线长为=5r,依题意,5r=10,∴r=2.因此圆台侧面积S=π(2+8)×10=100π.
6答案: 解析:方程x2-9x+18=0的两个根为x1=3,x2=6,
设侧面梯形的高为h,则由题意得×(3+6)·h×4=32+62,h=.
7答案:(5+)πa2 解析:S圆锥侧=π×a×=πa2,
S圆柱侧=2π×a×2a=4πa2,S底面=πa2,
∴S表=S圆锥侧+S圆柱侧+S底面
=5πa2+πa2=(5+)πa2.
8答案: 解析:如图,该几何体为底面为等腰直角三角形的直棱柱.由图知AB=AC,BC=,AB⊥AC.
∴S表=+2×2×2+2×=12+.
9答案:解:建筑物为一组合体,上面是底面半径为3米,母线长为5米的圆锥,下面是底面边长为3米,高为4米的正四棱柱.
圆锥的表面积=πr2+πrl
≈3.14×32+3.14×3×5
=28.26+47.1=75.36.
四棱柱的一个底面积=32=9,
四棱柱的侧面积=4×4×3=48.
所以外壁面积S≈75.36-9+48=114.36(平方米).
故需油漆114.36×0.2=22.872≈22.88(千克).
答:共需约22.88千克油漆.
10答案:解:(1)由三视图可知这个几何体是由两个圆柱夹一个圆台组成的,其中下面圆柱底面直径为60
mm,母线长40
mm,中间圆台上、下底直径分别为40
mm,60
mm,高为20
mm,上面圆柱的底面直径为20
mm,高为40
mm,其直观图如图所示.
(2)由三视图可知圆台母线长
(mm).
∴所求的表面积S=S下圆柱下底+S下圆柱侧+S圆台侧+(S圆台上底-S上圆柱下底)+S上圆柱侧+S上圆柱上底
=
=900π+2
400π+π+400π+800π
=(4
500π+π)(mm2)
=(45π+π)(cm2).
