1.7.2-1.7.3 棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积和球的表面积、体积 学案(含答案)
文档属性
| 名称 | 1.7.2-1.7.3 棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积和球的表面积、体积 学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览



文档简介
1.7.2 棱柱、棱锥、棱台和圆柱、圆锥、圆台的体积
1.7.3 球的表面积和体积
学案
课前预习导学
目标导航
学习目标
重点难点
1.在上一节学习的基础上,会用公式求柱、锥、台体的体积.了解柱、锥、台体的体积之间的关系.2.记住球的表面积和体积公式,并进行有关计算.3.通过学习,提高空间思维能力和空间想象能力,增强了探索问题和解决问题的信心.
重点:柱体、锥体、台体的体积的计算.会用公式求球的表面积和体积.难点:与球有关的组合体的体积计算.疑点:已知几何体的三视图,首先转化为直观图,再求它体积.
预习导引
1.柱、锥、台体的体积
V柱体=Sh(S为柱体的底面积,h为柱体的高).
V锥体=Sh(S为锥体的底面积,
h为锥体的高).
V台体=(S上+S下+)h(S上,S下分别为棱台的上,下底面积,h为高).
预习交流1
柱体、锥体、台体的体积公式有何联系?
提示:台体的体积公式中,如果设S上=S下,就得到柱体的体积公式V柱体=Sh;如果设S上=0,就得到锥体的体积公式V锥体=Sh.因此,柱体、锥体、台体的体积公式之间的关系,可表示如下.
由上可见,柱体、锥体的体积公式是台体的体积公式的特例.
预习交流2
(1)正棱锥的高和底面边长都缩小为原来的,则它的体积是原来的( ).
A. B.
C.
D.
(2)已知正六棱台的上、下底面边长分别为2和4,高为2,则其体积为________.
提示:(1)B (2)28
2.球的表面积和体积
S球面=4πR2,V球=πR3(其中R为球的半径).
预习交流3
(1)若球的半径由R增加为2R,则这个球的表面积变为原来的________倍,体积变为原来的________倍.
(2)若一个球的体积为4π,则它的表面积为______.
提示:(1)4 8 (2)12π
课堂合作探究
问题导学
1.柱体的体积
活动与探究1
如图①是一个水平放置的正三棱柱ABC A1B1C1,D是棱BC的中点.正三棱柱的主视图如图②.
求正三棱柱ABC A1B1C1的体积.
思路分析:由三视图可以得到正三棱柱的底面三角形的高和侧棱长.
解:由三视图可知:在正三棱柱中,AD=,AA1=3,从而在底面即等边△ABC中,AB===2,
所以正三棱柱的体积
V=Sh=×BC×AD×AA1=×2××3=3.
迁移与应用
1.圆柱的底面积是S,侧面展开图是一个正方形,则这个圆柱的体积是________.
解析:设圆柱的底面半径为r,
则S=πr2,∴r=,
则圆柱的母线长l=2πr=2,
即圆柱的高h=2,
∴V圆柱=S·h=2S.
答案:2S
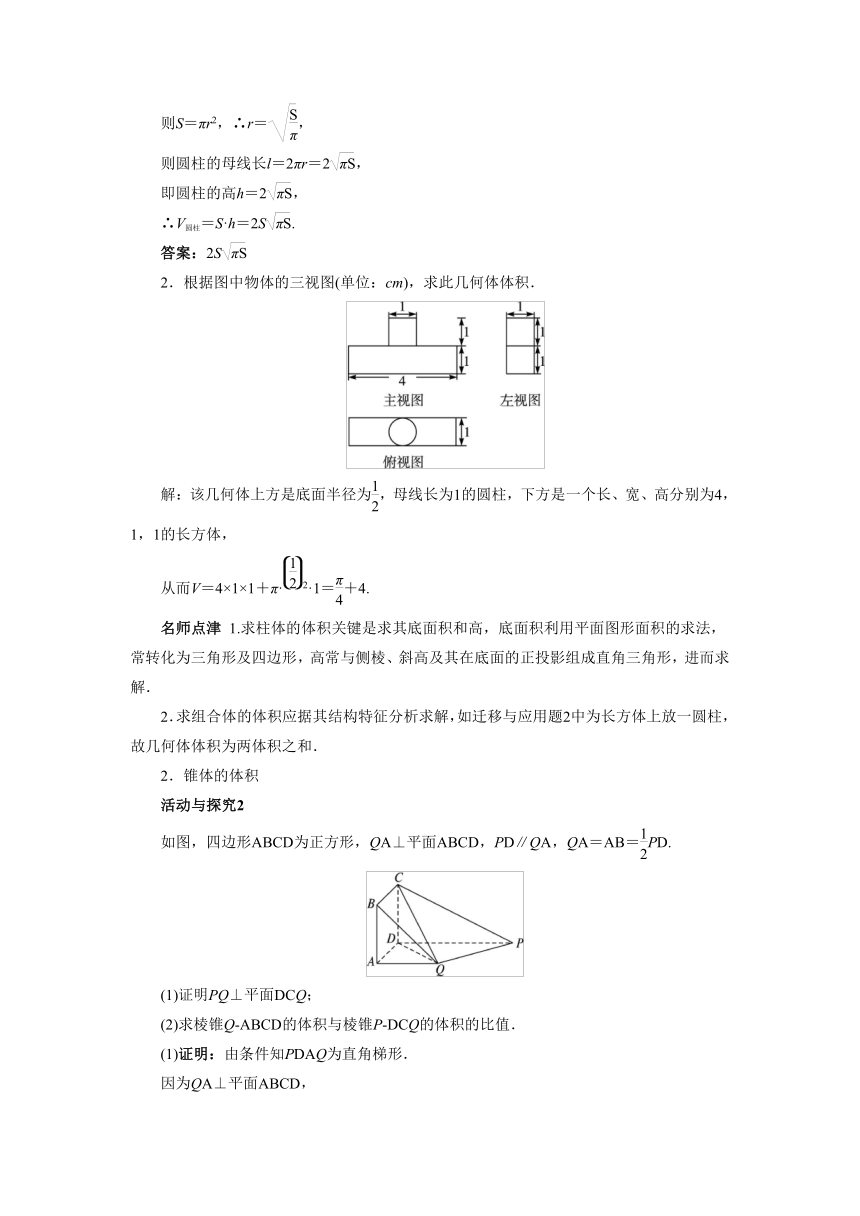
2.根据图中物体的三视图(单位:cm),求此几何体体积.
解:该几何体上方是底面半径为,母线长为1的圆柱,下方是一个长、宽、高分别为4,1,1的长方体,
从而V=4×1×1+π·2·1=+4.
名师点津
1.求柱体的体积关键是求其底面积和高,底面积利用平面图形面积的求法,常转化为三角形及四边形,高常与侧棱、斜高及其在底面的正投影组成直角三角形,进而求解.
2.求组合体的体积应据其结构特征分析求解,如迁移与应用题2中为长方体上放一圆柱,故几何体体积为两体积之和.
2.锥体的体积
活动与探究2
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD.
(1)证明PQ⊥平面DCQ;
(2)求棱锥Q ABCD的体积与棱锥P DCQ的体积的比值.
(1)证明:由条件知PDAQ为直角梯形.
因为QA⊥平面ABCD,
所以平面PDAQ⊥平面ABCD,交线为AD.
又四边形ABCD为正方形,DC⊥AD,
所以DC⊥平面PDAQ,可得PQ⊥DC.
在直角梯形PDAQ中可得DQ=PQ=PD,则PQ⊥QD.
所以PQ⊥平面DCQ.
(2)解:设AB=a.
由题设知AQ为棱锥Q ABCD的高,
所以棱锥Q ABCD的体积V1=a3.
由(1)知PQ为棱锥P DCQ的高.
而PQ=a,△DCQ的面积为a2,
所以棱锥P DCQ的体积V2=a3.
故棱锥Q ABCD的体积与棱锥P DCQ的体积的比值为1.
迁移与应用
1.某几何体的三视图如图所示,则它的体积为( ).
A.8-
B.8-
C.8-2π
D.
解析:由几何体的三视图可知,原几何体是一个棱长为2的正方体且内部去掉一个底面与正方体上底面内切,高等于正方体棱长的圆锥.正方体的体积为8,圆锥的体积为πr2h=,∴所求几何体的体积为8-.
答案:A
2.下图是一个正方体,H,G,F分别是棱AB,AD,AA1的中点.现在沿△GFH所在平面锯掉正方体的一个角,问锯掉的部分的体积是原正方体体积的几分之几?
解:设正方体的棱长为a,则正方体的体积为a3.三棱锥的底面是Rt△AGF,而∠FAG为90°,G,F分别为AD,AA1的中点,所以AF=AG=a.
所以△AGF的面积为×a×a=a2.
又AH是三棱锥的高,H又是AB的中点,
所以AH=a.
所以锯掉的部分的体积为×a×a2=a3.
又a3÷a3=,所以锯掉的部分的体积是原正方体体积的.
名师点津
(1)锥体的体积公式V=Sh既适合棱锥,也适合圆锥,其中棱锥可以是正棱锥,也可以不是正棱锥.
(2)三棱锥的体积求解具有较多的灵活性,因为三棱锥的任何一个面都可以作为底面,所以常常需要根据题目条件对其顶点和底面进行转换,这一方法叫做等积法.
3.台体的体积
活动与探究3
如图,三棱柱ABC A1B1C1中,若E,F分别为AB,AC的中点,平面EB1C1F将三棱柱分成体积为V1,V2的两部分,那么V1∶V2=__________.
思路分析:V1对应的几何体AEF A1B1C1是一个棱台,一个底面的面积与棱柱的底面积相等,另一个底面的面积等于棱柱底面积的;V2对应的是一个不规则几何体,显然V2无法直接表示,可以考虑间接的办法,用三棱柱的体积减去V1来表示.
解析:设三棱柱的高为h,底面的面积为S,体积为V,则V=V1+V2=Sh.
因为E,F分别为AB,AC的中点,
所以S△AEF=S,
V2=Sh-V1=Sh,故V1∶V2=7∶5.
答案:7∶5
迁移与应用
四边形ABCD中,A(0,0),B(1,0),C(2,1),D(0,3),绕y轴旋转一周,求所得旋转体的体积.
解:∵C(2,1),D(0,3),
∴圆锥的底面半径r=2,高h=2.
∴V圆锥=πr2h=×22×2=.
∵B(1,0),C(2,1),
∴圆台的两个底面半径R=2,R′=1,高h′=1.
∴V圆台=
(R2+R′2+RR′)
=×1×(22+12+2×1)=
,
∴V=V圆锥+V圆台=5π.
名师点津
求不规则几何体的体积可通过对几何体分割,使每部分能够易求得其体积,也可将其“补”成规则几何体,使所求体积等于整体几何体的体积减去部分几何体的体积,这就是我们常说的割补法,是解决此类问题的常用方法,还要注意不同的割补方式会得到不同的几何体,做题时要仔细观察.
4.球的表面积和体积
活动与探究4
(1)设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( ).
A.3πa2
B.6πa2
C.12πa2
D.24πa2
(2)如果三个球的半径之比是1∶2∶3,那么最大球的体积是其余两个球的体积之和的( ).
A.1倍
B.2倍
C.3倍
D.4倍
思路分析:(1)该球的直径等于长方体的体对角线长.
(2)可设出球的半径,计算出三个球的体积,然后求得结论.
解析:(1)由于长方体的长、宽、高分别为2a,a,
a,则长方体的体对角线长为=a.又长方体外接球的直径2R等于长方体的体对角线,∴2R=a.
∴S球=4πR2=6πa2.
(2)半径大的球的体积也大,设三个球的半径分别为x,2x,3x,则最大球的半径为3x,其体积为π×(3x)3,其余两个球的体积之和为πx3+π×(2x)3,
∴π×(3x)3÷=3.
答案:(1)B (2)C
迁移与应用
1.如图是某几何体的三视图,则该几何体的体积为( ).
A.π+12
B.π+18
C.9π+42
D.36π+18
分析:由题意知该几何体上部为直径为3的球,下部为长、宽、高分别为3,3,2的长方体
答案:B
2.请用所学知识探求表面积相等的球和正方体,哪个体积更大.
解:设球的半径为r,正方体的棱长为a,依题意得4πr2=6a2,所以r=a.所以V球=π3=a3.
又因为V正方体=a3,且>1,所以V球>V正方体,
即球的体积大于正方体的体积.
名师点津
计算球的表面积和体积时要注意的问题:
(1)关键是计算球的半径,而计算半径的关键是寻找球心的位置.因此,在解题过程中要特别关注题目中所揭示的球心位置,球面上的点等信息.
(2)当球的半径增加为原来的2倍时,球的表面积增加为原来的4倍,球的体积增加为原来的8倍.
(3)注意公式的“双向”应用,也就是说当知道球的表面积或体积时,也可以求出球的半径.
当堂检测
1.
已知高为3的直三棱柱ABC A′B′C′的底面是边长为1的正三角形,则三棱锥B′ ABC的体积为( ).
A.
B.
C.
D.
解析:由题意知S△ABC=×12=,
∴VB′ ABC=S△ABC×3=.
答案:D
2.已知两个球的半径之比为1∶2,则这两个球的表面积之比为( ).
A.1∶2
B.1∶4
C.1∶6
D.1∶8
解析:由S=4πr2知,若半径之比为1∶2,则表面积之比为1∶4.
答案:B
3.圆台的上、下底面的面积分别为π,4π,侧面积是6π,这个圆台的体积是( ).
A.
B.2π
C.
D.
解析:设上、下底面半径为r′,r,母线长为l,
则∴
圆台的高h==,
∴V圆台=(π++4π)·=.
答案:D
4.一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是( ).
A.4
B.2
C.2
D.
解析:由题意可设棱柱的底面边长为a,
则其体积为a2·a=2,得a=2.
由俯视图易知,三棱柱的左视图是以2为长,为宽的矩形.∴其面积为2.故选B.
答案:B
5.如图,一个底面直径为20
cm的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6
cm,高为20
cm的一个圆锥形铅锤,当铅锤从水中取出后,杯里的水将下降几厘米?(π≈3.14)
解:设水面下降的高度为x
cm,因为圆锥形铅锤的体积为×20=60π(cm3),
则小圆柱的体积为π×(20÷2)2×x=100πx(cm3).
所以60π=100πx,解得x=0.6(cm).
则铅锤取出后,杯中水面下降了0.6
cm.
1.7.3 球的表面积和体积
学案
课前预习导学
目标导航
学习目标
重点难点
1.在上一节学习的基础上,会用公式求柱、锥、台体的体积.了解柱、锥、台体的体积之间的关系.2.记住球的表面积和体积公式,并进行有关计算.3.通过学习,提高空间思维能力和空间想象能力,增强了探索问题和解决问题的信心.
重点:柱体、锥体、台体的体积的计算.会用公式求球的表面积和体积.难点:与球有关的组合体的体积计算.疑点:已知几何体的三视图,首先转化为直观图,再求它体积.
预习导引
1.柱、锥、台体的体积
V柱体=Sh(S为柱体的底面积,h为柱体的高).
V锥体=Sh(S为锥体的底面积,
h为锥体的高).
V台体=(S上+S下+)h(S上,S下分别为棱台的上,下底面积,h为高).
预习交流1
柱体、锥体、台体的体积公式有何联系?
提示:台体的体积公式中,如果设S上=S下,就得到柱体的体积公式V柱体=Sh;如果设S上=0,就得到锥体的体积公式V锥体=Sh.因此,柱体、锥体、台体的体积公式之间的关系,可表示如下.
由上可见,柱体、锥体的体积公式是台体的体积公式的特例.
预习交流2
(1)正棱锥的高和底面边长都缩小为原来的,则它的体积是原来的( ).
A. B.
C.
D.
(2)已知正六棱台的上、下底面边长分别为2和4,高为2,则其体积为________.
提示:(1)B (2)28
2.球的表面积和体积
S球面=4πR2,V球=πR3(其中R为球的半径).
预习交流3
(1)若球的半径由R增加为2R,则这个球的表面积变为原来的________倍,体积变为原来的________倍.
(2)若一个球的体积为4π,则它的表面积为______.
提示:(1)4 8 (2)12π
课堂合作探究
问题导学
1.柱体的体积
活动与探究1
如图①是一个水平放置的正三棱柱ABC A1B1C1,D是棱BC的中点.正三棱柱的主视图如图②.
求正三棱柱ABC A1B1C1的体积.
思路分析:由三视图可以得到正三棱柱的底面三角形的高和侧棱长.
解:由三视图可知:在正三棱柱中,AD=,AA1=3,从而在底面即等边△ABC中,AB===2,
所以正三棱柱的体积
V=Sh=×BC×AD×AA1=×2××3=3.
迁移与应用
1.圆柱的底面积是S,侧面展开图是一个正方形,则这个圆柱的体积是________.
解析:设圆柱的底面半径为r,
则S=πr2,∴r=,
则圆柱的母线长l=2πr=2,
即圆柱的高h=2,
∴V圆柱=S·h=2S.
答案:2S
2.根据图中物体的三视图(单位:cm),求此几何体体积.
解:该几何体上方是底面半径为,母线长为1的圆柱,下方是一个长、宽、高分别为4,1,1的长方体,
从而V=4×1×1+π·2·1=+4.
名师点津
1.求柱体的体积关键是求其底面积和高,底面积利用平面图形面积的求法,常转化为三角形及四边形,高常与侧棱、斜高及其在底面的正投影组成直角三角形,进而求解.
2.求组合体的体积应据其结构特征分析求解,如迁移与应用题2中为长方体上放一圆柱,故几何体体积为两体积之和.
2.锥体的体积
活动与探究2
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD.
(1)证明PQ⊥平面DCQ;
(2)求棱锥Q ABCD的体积与棱锥P DCQ的体积的比值.
(1)证明:由条件知PDAQ为直角梯形.
因为QA⊥平面ABCD,
所以平面PDAQ⊥平面ABCD,交线为AD.
又四边形ABCD为正方形,DC⊥AD,
所以DC⊥平面PDAQ,可得PQ⊥DC.
在直角梯形PDAQ中可得DQ=PQ=PD,则PQ⊥QD.
所以PQ⊥平面DCQ.
(2)解:设AB=a.
由题设知AQ为棱锥Q ABCD的高,
所以棱锥Q ABCD的体积V1=a3.
由(1)知PQ为棱锥P DCQ的高.
而PQ=a,△DCQ的面积为a2,
所以棱锥P DCQ的体积V2=a3.
故棱锥Q ABCD的体积与棱锥P DCQ的体积的比值为1.
迁移与应用
1.某几何体的三视图如图所示,则它的体积为( ).
A.8-
B.8-
C.8-2π
D.
解析:由几何体的三视图可知,原几何体是一个棱长为2的正方体且内部去掉一个底面与正方体上底面内切,高等于正方体棱长的圆锥.正方体的体积为8,圆锥的体积为πr2h=,∴所求几何体的体积为8-.
答案:A
2.下图是一个正方体,H,G,F分别是棱AB,AD,AA1的中点.现在沿△GFH所在平面锯掉正方体的一个角,问锯掉的部分的体积是原正方体体积的几分之几?
解:设正方体的棱长为a,则正方体的体积为a3.三棱锥的底面是Rt△AGF,而∠FAG为90°,G,F分别为AD,AA1的中点,所以AF=AG=a.
所以△AGF的面积为×a×a=a2.
又AH是三棱锥的高,H又是AB的中点,
所以AH=a.
所以锯掉的部分的体积为×a×a2=a3.
又a3÷a3=,所以锯掉的部分的体积是原正方体体积的.
名师点津
(1)锥体的体积公式V=Sh既适合棱锥,也适合圆锥,其中棱锥可以是正棱锥,也可以不是正棱锥.
(2)三棱锥的体积求解具有较多的灵活性,因为三棱锥的任何一个面都可以作为底面,所以常常需要根据题目条件对其顶点和底面进行转换,这一方法叫做等积法.
3.台体的体积
活动与探究3
如图,三棱柱ABC A1B1C1中,若E,F分别为AB,AC的中点,平面EB1C1F将三棱柱分成体积为V1,V2的两部分,那么V1∶V2=__________.
思路分析:V1对应的几何体AEF A1B1C1是一个棱台,一个底面的面积与棱柱的底面积相等,另一个底面的面积等于棱柱底面积的;V2对应的是一个不规则几何体,显然V2无法直接表示,可以考虑间接的办法,用三棱柱的体积减去V1来表示.
解析:设三棱柱的高为h,底面的面积为S,体积为V,则V=V1+V2=Sh.
因为E,F分别为AB,AC的中点,
所以S△AEF=S,
V2=Sh-V1=Sh,故V1∶V2=7∶5.
答案:7∶5
迁移与应用
四边形ABCD中,A(0,0),B(1,0),C(2,1),D(0,3),绕y轴旋转一周,求所得旋转体的体积.
解:∵C(2,1),D(0,3),
∴圆锥的底面半径r=2,高h=2.
∴V圆锥=πr2h=×22×2=.
∵B(1,0),C(2,1),
∴圆台的两个底面半径R=2,R′=1,高h′=1.
∴V圆台=
(R2+R′2+RR′)
=×1×(22+12+2×1)=
,
∴V=V圆锥+V圆台=5π.
名师点津
求不规则几何体的体积可通过对几何体分割,使每部分能够易求得其体积,也可将其“补”成规则几何体,使所求体积等于整体几何体的体积减去部分几何体的体积,这就是我们常说的割补法,是解决此类问题的常用方法,还要注意不同的割补方式会得到不同的几何体,做题时要仔细观察.
4.球的表面积和体积
活动与探究4
(1)设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( ).
A.3πa2
B.6πa2
C.12πa2
D.24πa2
(2)如果三个球的半径之比是1∶2∶3,那么最大球的体积是其余两个球的体积之和的( ).
A.1倍
B.2倍
C.3倍
D.4倍
思路分析:(1)该球的直径等于长方体的体对角线长.
(2)可设出球的半径,计算出三个球的体积,然后求得结论.
解析:(1)由于长方体的长、宽、高分别为2a,a,
a,则长方体的体对角线长为=a.又长方体外接球的直径2R等于长方体的体对角线,∴2R=a.
∴S球=4πR2=6πa2.
(2)半径大的球的体积也大,设三个球的半径分别为x,2x,3x,则最大球的半径为3x,其体积为π×(3x)3,其余两个球的体积之和为πx3+π×(2x)3,
∴π×(3x)3÷=3.
答案:(1)B (2)C
迁移与应用
1.如图是某几何体的三视图,则该几何体的体积为( ).
A.π+12
B.π+18
C.9π+42
D.36π+18
分析:由题意知该几何体上部为直径为3的球,下部为长、宽、高分别为3,3,2的长方体
答案:B
2.请用所学知识探求表面积相等的球和正方体,哪个体积更大.
解:设球的半径为r,正方体的棱长为a,依题意得4πr2=6a2,所以r=a.所以V球=π3=a3.
又因为V正方体=a3,且>1,所以V球>V正方体,
即球的体积大于正方体的体积.
名师点津
计算球的表面积和体积时要注意的问题:
(1)关键是计算球的半径,而计算半径的关键是寻找球心的位置.因此,在解题过程中要特别关注题目中所揭示的球心位置,球面上的点等信息.
(2)当球的半径增加为原来的2倍时,球的表面积增加为原来的4倍,球的体积增加为原来的8倍.
(3)注意公式的“双向”应用,也就是说当知道球的表面积或体积时,也可以求出球的半径.
当堂检测
1.
已知高为3的直三棱柱ABC A′B′C′的底面是边长为1的正三角形,则三棱锥B′ ABC的体积为( ).
A.
B.
C.
D.
解析:由题意知S△ABC=×12=,
∴VB′ ABC=S△ABC×3=.
答案:D
2.已知两个球的半径之比为1∶2,则这两个球的表面积之比为( ).
A.1∶2
B.1∶4
C.1∶6
D.1∶8
解析:由S=4πr2知,若半径之比为1∶2,则表面积之比为1∶4.
答案:B
3.圆台的上、下底面的面积分别为π,4π,侧面积是6π,这个圆台的体积是( ).
A.
B.2π
C.
D.
解析:设上、下底面半径为r′,r,母线长为l,
则∴
圆台的高h==,
∴V圆台=(π++4π)·=.
答案:D
4.一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是( ).
A.4
B.2
C.2
D.
解析:由题意可设棱柱的底面边长为a,
则其体积为a2·a=2,得a=2.
由俯视图易知,三棱柱的左视图是以2为长,为宽的矩形.∴其面积为2.故选B.
答案:B
5.如图,一个底面直径为20
cm的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6
cm,高为20
cm的一个圆锥形铅锤,当铅锤从水中取出后,杯里的水将下降几厘米?(π≈3.14)
解:设水面下降的高度为x
cm,因为圆锥形铅锤的体积为×20=60π(cm3),
则小圆柱的体积为π×(20÷2)2×x=100πx(cm3).
所以60π=100πx,解得x=0.6(cm).
则铅锤取出后,杯中水面下降了0.6
cm.
