1.7.3 球的表面积和体积 同步练习2(含答案)
文档属性
| 名称 | 1.7.3 球的表面积和体积 同步练习2(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览

文档简介
1.7.3
球的表面积和体积
同步练习
课后训练
1.用与球心距离为1的平面去截球,所得截面面积为π,则球的表面积为( ).
A.π
B.2π
C.4π
D.8π
2.把3个半径为R的铁球熔成一个底面半径为R的圆柱,则圆柱的高为( ).
A.R
B.2R
C.3R
D.4R
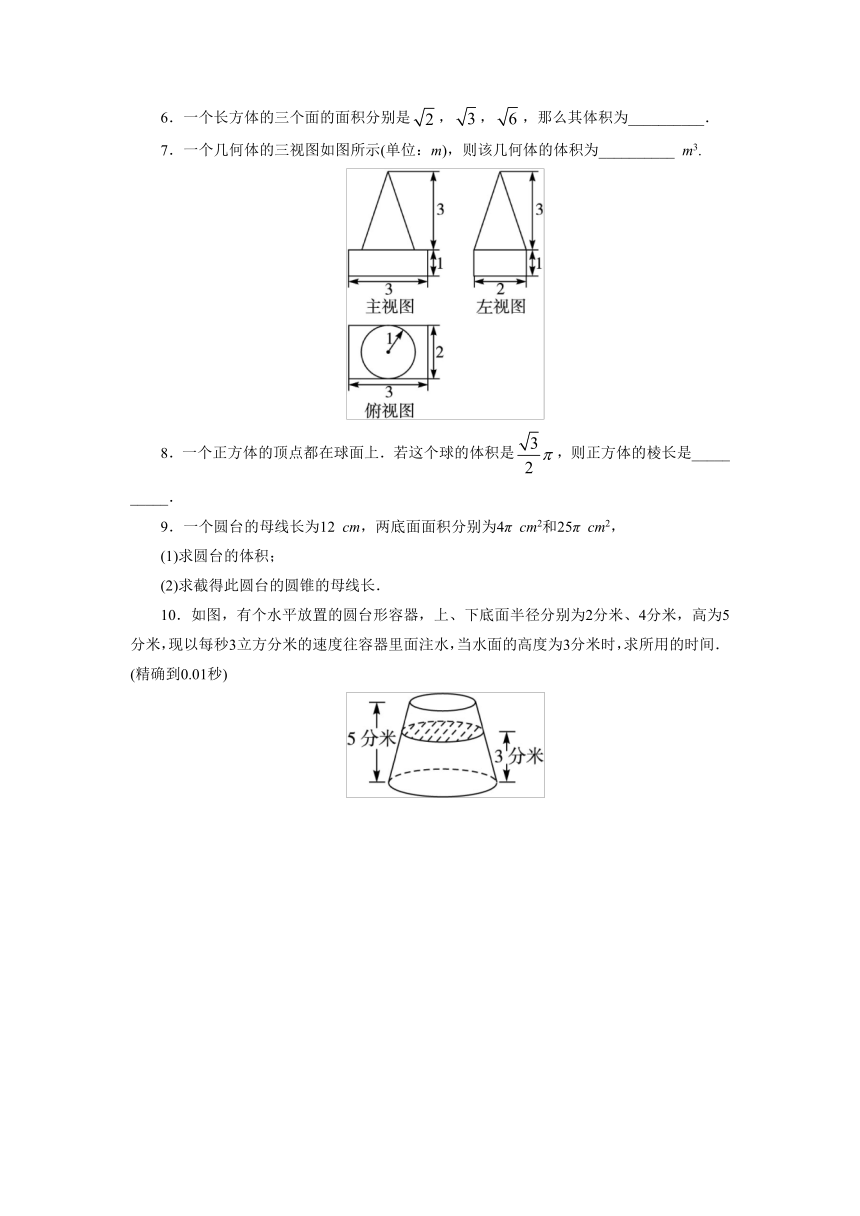
3.如图,在棱长为4的正方体ABCD-A1B1C1D1中,P是A1B1上一点,且PB1=A1B1,则四棱锥P-BCC1B1的体积为( ).
A.
B.
C.
4
D.16
4.长方体一个顶点上的三条棱长分别是3,4,5,且它的8个顶点都在同一个球面上,则这个球的表面积是( ).
A.π
B.π
C.50π
D.200π
5.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( ).
A.cm3
B.144
cm3
C.cm3
D.cm3
6.一个长方体的三个面的面积分别是,,,那么其体积为__________.
7.一个几何体的三视图如图所示(单位:m),则该几何体的体积为__________
m3.
8.一个正方体的顶点都在球面上.若这个球的体积是,则正方体的棱长是__________.
9.一个圆台的母线长为12
cm,两底面面积分别为4π
cm2和25π
cm2,
(1)求圆台的体积;
(2)求截得此圆台的圆锥的母线长.
10.如图,有个水平放置的圆台形容器,上、下底面半径分别为2分米、4分米,高为5分米,现以每秒3立方分米的速度往容器里面注水,当水面的高度为3分米时,求所用的时间.
(精确到0.01秒)
参考答案
1答案:D 解析:所得截面圆的半径为r=1,因此球的半径,球的表面积为.
2答案:D 解析:设圆柱的高为h,则,∴h=4R.
3答案:B 解析:四棱锥P-BCC1B1的底面是正方体的侧面,高PB1=A1B1=1,则VP-BCC1B1=×42×1=.
4答案:C 解析:设球的半径为R,则.
∴S球=4πR2=π·(2R)2=50π.
5答案:B 解析:该几何体是一个组合体,上面是一个正四棱柱,其底面是边长为4的正方形,且高为2,下面是一个正四棱台,其高为3,下底面是边长为8的正方形,所以V=4×4×2+×3×(64+16+)=144(cm3).
6答案: 解析:设长方体的长、宽、高分别为a,b,c,则不妨令ab=,ac=,bc=,于是(abc)2==6,因此V=abc=.
7答案:6+π 解析:由几何体的三视图可知,原几何体是一个长方体和一个圆锥的组合体.下面的长方体的长、宽、高分别是3
m,2
m,1
m,∴体积为3×2×1=6(m3).
上面的圆锥底面圆半径为1
m,高为3
m,∴圆锥的体积为π×12×3=π(m3).∴该几何体的体积为(6+π)
m3.
8答案:1 解析:设球的半径为r,则,所以,,球的直径为,设正方体的棱长为a,因为正方体内接于球,故3a2=()2,所以a=1.
9答案:解:(1)如图,圆台的轴截面是等腰梯形ABCD,由上、下底面面积分别为4π
cm2,25π
cm2得,上底半径O1A=2
cm,下底半径OB=5
cm,
又∵腰长为12
cm,∴圆台的高AM==
(cm),
∴圆台的体积=(S上++S下)h=(4π++25π)·=π(cm3).
(2)设截得此圆台的圆锥母线长为l
cm,则由△SAO1∽△SBO得,∴l=20(cm),即截得此圆台的圆锥母线长为20
cm.
10答案:解:如图,设水面的半径为r分米,则EH=(r-2)分米,BG=2分米,在△ABG中,
∵EH∥BG,∴.
∵AH=2分米,∴.
∴r=(分米).
∴当水面的高度为3分米时,容器中水的体积为
(分米3).
∴所用的时间为≈36.
69(秒).
∴所用的时间约为36.69秒.
球的表面积和体积
同步练习
课后训练
1.用与球心距离为1的平面去截球,所得截面面积为π,则球的表面积为( ).
A.π
B.2π
C.4π
D.8π
2.把3个半径为R的铁球熔成一个底面半径为R的圆柱,则圆柱的高为( ).
A.R
B.2R
C.3R
D.4R
3.如图,在棱长为4的正方体ABCD-A1B1C1D1中,P是A1B1上一点,且PB1=A1B1,则四棱锥P-BCC1B1的体积为( ).
A.
B.
C.
4
D.16
4.长方体一个顶点上的三条棱长分别是3,4,5,且它的8个顶点都在同一个球面上,则这个球的表面积是( ).
A.π
B.π
C.50π
D.200π
5.若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( ).
A.cm3
B.144
cm3
C.cm3
D.cm3
6.一个长方体的三个面的面积分别是,,,那么其体积为__________.
7.一个几何体的三视图如图所示(单位:m),则该几何体的体积为__________
m3.
8.一个正方体的顶点都在球面上.若这个球的体积是,则正方体的棱长是__________.
9.一个圆台的母线长为12
cm,两底面面积分别为4π
cm2和25π
cm2,
(1)求圆台的体积;
(2)求截得此圆台的圆锥的母线长.
10.如图,有个水平放置的圆台形容器,上、下底面半径分别为2分米、4分米,高为5分米,现以每秒3立方分米的速度往容器里面注水,当水面的高度为3分米时,求所用的时间.
(精确到0.01秒)
参考答案
1答案:D 解析:所得截面圆的半径为r=1,因此球的半径,球的表面积为.
2答案:D 解析:设圆柱的高为h,则,∴h=4R.
3答案:B 解析:四棱锥P-BCC1B1的底面是正方体的侧面,高PB1=A1B1=1,则VP-BCC1B1=×42×1=.
4答案:C 解析:设球的半径为R,则.
∴S球=4πR2=π·(2R)2=50π.
5答案:B 解析:该几何体是一个组合体,上面是一个正四棱柱,其底面是边长为4的正方形,且高为2,下面是一个正四棱台,其高为3,下底面是边长为8的正方形,所以V=4×4×2+×3×(64+16+)=144(cm3).
6答案: 解析:设长方体的长、宽、高分别为a,b,c,则不妨令ab=,ac=,bc=,于是(abc)2==6,因此V=abc=.
7答案:6+π 解析:由几何体的三视图可知,原几何体是一个长方体和一个圆锥的组合体.下面的长方体的长、宽、高分别是3
m,2
m,1
m,∴体积为3×2×1=6(m3).
上面的圆锥底面圆半径为1
m,高为3
m,∴圆锥的体积为π×12×3=π(m3).∴该几何体的体积为(6+π)
m3.
8答案:1 解析:设球的半径为r,则,所以,,球的直径为,设正方体的棱长为a,因为正方体内接于球,故3a2=()2,所以a=1.
9答案:解:(1)如图,圆台的轴截面是等腰梯形ABCD,由上、下底面面积分别为4π
cm2,25π
cm2得,上底半径O1A=2
cm,下底半径OB=5
cm,
又∵腰长为12
cm,∴圆台的高AM==
(cm),
∴圆台的体积=(S上++S下)h=(4π++25π)·=π(cm3).
(2)设截得此圆台的圆锥母线长为l
cm,则由△SAO1∽△SBO得,∴l=20(cm),即截得此圆台的圆锥母线长为20
cm.
10答案:解:如图,设水面的半径为r分米,则EH=(r-2)分米,BG=2分米,在△ABG中,
∵EH∥BG,∴.
∵AH=2分米,∴.
∴r=(分米).
∴当水面的高度为3分米时,容器中水的体积为
(分米3).
∴所用的时间为≈36.
69(秒).
∴所用的时间约为36.69秒.
