1.7.3 球的表面积和体积 学案2(含答案)
文档属性
| 名称 | 1.7.3 球的表面积和体积 学案2(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览



文档简介
1.7.3 球的表面积和体积
学案
问题导学
1.柱体的体积
活动与探究1
如图①是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的主视图如图②.
求正三棱柱ABC-A1B1C1的体积.
迁移与应用
1.一个圆柱的侧面展开图是一个边长为4π的正方形,则这个圆柱的体积为__________.
2.根据图中物体的三视图(单位:cm),求此几何体体积.
名师点津
1.求柱体的体积关键是求其底面积和高,底面积利用平面图形面积的求法,常转化为三角形及四边形,高常与侧棱、斜高及其在底面的正投影组成直角三角形,进而求解.
2.求组合体的体积应据其结构特征分析求解,如迁移与应用题2中为长方体上放一圆柱,故几何体体积为两体积之和.
2.锥体的体积
活动与探究2
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD.
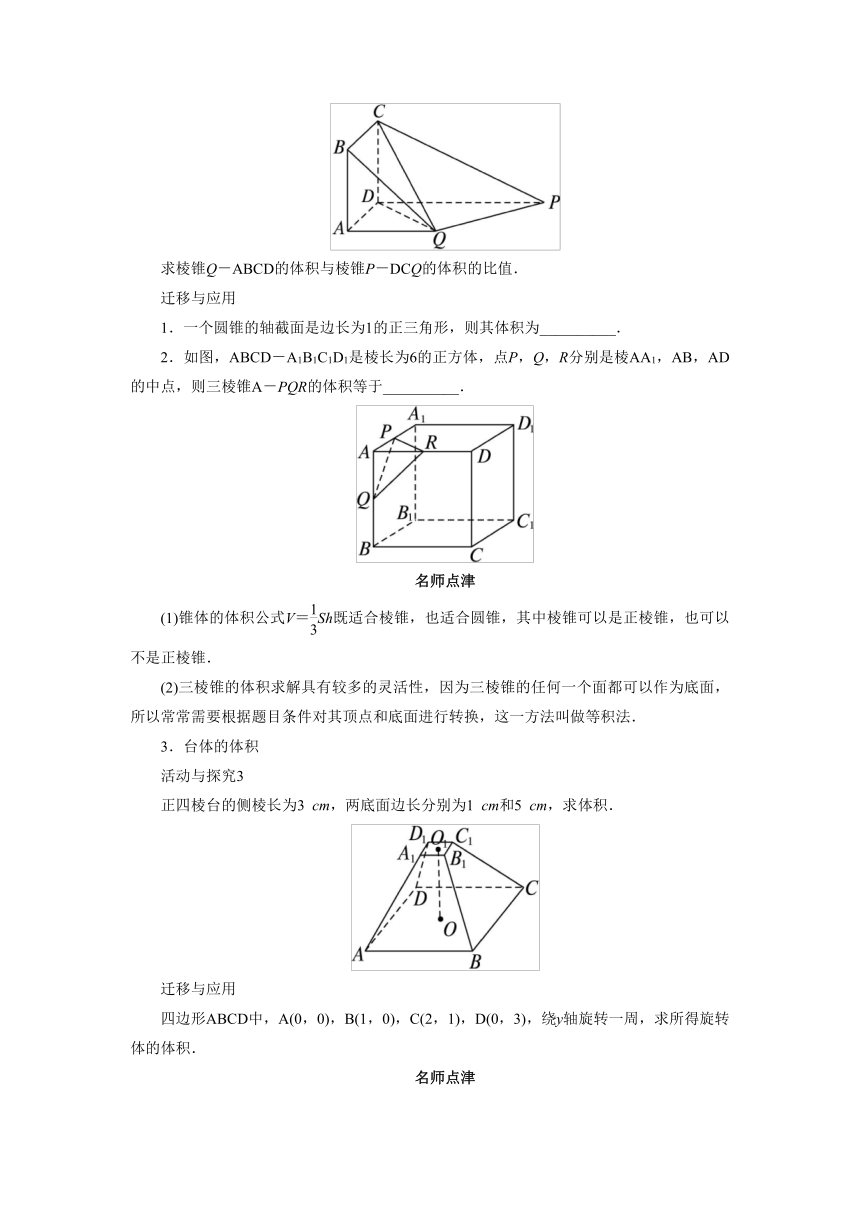
求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.
迁移与应用
1.一个圆锥的轴截面是边长为1的正三角形,则其体积为__________.
2.如图,ABCD-A1B1C1D1是棱长为6的正方体,点P,Q,R分别是棱AA1,AB,AD的中点,则三棱锥A-PQR的体积等于__________.
名师点津
(1)锥体的体积公式V=Sh既适合棱锥,也适合圆锥,其中棱锥可以是正棱锥,也可以不是正棱锥.
(2)三棱锥的体积求解具有较多的灵活性,因为三棱锥的任何一个面都可以作为底面,所以常常需要根据题目条件对其顶点和底面进行转换,这一方法叫做等积法.
3.台体的体积
活动与探究3
正四棱台的侧棱长为3
cm,两底面边长分别为1
cm和5
cm,求体积.
迁移与应用
四边形ABCD中,A(0,0),B(1,0),C(2,1),D(0,3),绕y轴旋转一周,求所得旋转体的体积.
名师点津
1.求台体的体积的一般方法是求出台体的上、下底面的面积和高,然后套用公式V=(S′++S)h计算求解.
2.由于台体可以看作是由一个平行于锥体底面的平面截去小锥体后剩余的部分,因此台体的体积也可以由大锥体的体积减去小锥体的体积来计算得到.
4.球的表面积和体积
活动与探究4
(1)设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( ).
A.3πa2
B.6πa2
C.12πa2
D.24πa2
(2)如果三个球的半径之比是1∶2∶3,那么最大球的体积是其余两个球的体积之和的( ).
A.1倍
B.2倍
C.3倍
D.4倍
迁移与应用
1.若一个球的体积为4π,则它的表面积为________.
2.如图是某几何体的三视图,则该几何体的体积为( ).
A.π+12
B.π+18
C.9π+42
D.36π+18
名师点津
计算球的表面积和体积时要注意的问题:
(1)关键是计算球的半径,而计算半径的关键是寻找球心的位置.因此,在解题过程中要特别关注题目中所揭示的球心位置,球面上的点等信息.
(2)当球的半径增加为原来的2倍时,球的表面积增加为原来的4倍,球的体积增加为原来的8倍.
(3)注意公式的“双向”应用,也就是说当知道球的表面积或体积时,也可以求出球的半径.
当堂检测
1.已知高为3的直三棱柱ABC-A′B′C′的底面是边长为1的正三角形,则三棱锥B′-ABC的体积为( ).
A.
B.
C.
D.
2.已知两个球的半径之比为1∶2,则这两个球的表面积之比为( ).
A.1∶2
B.1∶4
C.1∶6
D.1∶8
3.圆台的上、下底面的面积分别为π,4π,侧面积是6π,这个圆台的体积是( ).
A.
B.2π
C.
D.
4.将两个棱长为10
cm的正方体铜块熔化后铸成底面边长为5
cm的正四棱柱,则该四棱柱的高为( ).
A.8
cm
B.80
cm
C.40
cm
D.
cm
5.如图,一个底面直径为20
cm的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6
cm,高为20
cm的一个圆锥形铅锤,当铅锤从水中取出后,杯里的水将下降几厘米?(π≈3.14)
盘点收获
提示:用最精练的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记.
答案:
课前预习导学
预习导引
预习交流1 提示:台体的体积公式中,如果S上=S下,就得到柱体的体积公式V柱体=Sh;如果S上=0,就得到锥体的体积公式V锥体=Sh.因此,柱体、锥体、台体的体积公式之间的关系,可表示如下.
由上图可见,柱体、锥体的体积公式是台体的体积公式的特例.
预习交流2 提示:体积相等,都等于Sh.
预习交流3 提示:V圆柱=πR2h,V圆锥=πR2h.
预习交流4 提示:表面积扩大为原来的4倍,体积扩大为原来的8倍.
课堂合作探究
问题导学
活动与探究1 思路分析:由三视图可以得到正三棱柱的底面三角形的高和侧棱长,从而可求出正三棱柱的底面边长与高,然后套用体积公式计算.
解:由三视图可知:在正三棱柱中,AD=,AA1=3,从而在底面即等边△ABC中,AB===2,所以正三棱柱的体积V=Sh=×BC×AD×AA1=×2××3=3.
迁移与应用 1.16π2 解析:设圆柱的底面半径为r,高为h,依题意有2πr=4π,h=4π,所以r=2,于是体积V=Sh=πr2h=π·22·4π=16π2.
2.解:该几何体上方是底面半径为,母线长为1的圆柱,下方是一个长、宽、高分别为4,1,1的长方体,
从而V=4×1×1+π·2·1=+4.
活动与探究2 思路分析:对于棱锥Q-ABCD,其底面为正方形ABCD,高即为QA,易求体积;对于三棱锥P-DCQ,若以△DCQ为底面,则应证明PQ是其高,然后再计算,也可将三角形CDP作为底面,这时其高易证即为AD,从而可求体积.
解:设AB=a.由题意知AQ即为棱锥Q-ABCD的高,
所以棱锥Q-ABCD的体积V1=Sh=×a2×a=a3.
方法1:由于棱锥P-DCQ与棱锥Q-CDP是同一个棱锥,其体积相等,
而其底面是Rt△CDP,面积为S1=×a×2a=a2.
取DP中点N,连接QN,则QN∥AD,
又AD⊥DC,AD⊥DP,
所以AD⊥平面CDP,
故QN⊥平面CDP.
因此QN就是三棱锥Q-CDP的高,且QN=AD=a.
于是棱锥P-DCQ的体积V2=VQ-CDP=×a×a2=a3.
于是V1∶V2=1.
方法2:因为QA⊥平面ABCD,
所以平面PDAQ⊥平面ABCD,交线为AD.
又四边形ABCD为正方形,DC⊥AD,
所以DC⊥平面PDAQ.于是得PQ⊥DC.
在直角梯形PDAQ中,可得DQ=PQ=PD,则PQ⊥QD,所以PQ⊥平面DCQ.
即PQ为三棱锥P-DCQ的高,且PQ=a,
而△DCQ的面积为·a·a=a2,
所以三棱锥P-DCQ的体积V2=·a2·a=a3,
于是V1∶V2=1.
迁移与应用 1.π 解析:依题意,圆锥的底面半径为,高为,于是体积V=π·2·=π.
2. 解析:VA-PQR=VQ-APR=S△APR·AQ=××3×3×3=.
活动与探究3 思路分析:解答本题的关键是利用侧棱与高构成的直角梯形求出台体的高,进而求出正四棱台的体积.
解:正四棱台ABCD-A1B1C1D1中O1,O分别是两底面的中心.
∵A1C1=,AC=5,
∴A1O1=,AO=,
∴O1O==1,
V=×1×(12+52+)
=(1+25+5)=(cm3).
迁移与应用 解:∵C(2,1),D(0,3),
∴圆锥的底面半径r=2,高h=2.
∴V圆锥=πr2h=π×22×2=π.
∵B(1,0),C(2,1),
∴圆台的两个底面半径R=2,R′=1,高h′=1.
∴V圆台=πh′(R2+R′2+RR′)
=π×1×(22+12+2×1)=π,
∴V=V圆锥+V圆台=5π.
活动与探究4 思路分析:(1)该球的直径等于长方体的体对角线长.
(2)可设出球的半径,计算出三个球的体积,然后求得结论.
(1)B
(2)C 解析:(1)由于长方体的长、宽、高分别为2a,a,a,则长方体的体对角线长为=a.又长方体外接球的直径2R等于长方体的体对角线,∴2R=a.
∴S球=4πR2=6πa2.
(2)半径大的球的体积也大,设三个球的半径分别为x,2x,3x,则最大球的半径为3x,其体积为π×(3x)3,其余两个球的体积之和为πx3+π×(2x)3,
∴π×(3x)3÷=3.
迁移与应用 1.12π 解析:设球的半径为
R,由R3=4π,得R=,所以S=4πR2=12π.
2.B 解析:由题意知该几何体上部为直径为3的球,下部为长、宽、高分别为3,3,2的长方体,∴该几何体的体积为V=π×2+3×3×2=+18.
当堂检测
1.D 2.B 3.D 4.B
5.解:设水面下降的高度为x
cm,因为圆锥形铅锤的体积为×π×2×20=60π(cm3),
小圆柱的体积为π×(20÷2)2×x=100πx(cm3).
所以60π=100πx,解得x=0.6(cm).则铅锤取出后,杯中水面下降了0.6
cm.
学案
问题导学
1.柱体的体积
活动与探究1
如图①是一个水平放置的正三棱柱ABC-A1B1C1,D是棱BC的中点.正三棱柱的主视图如图②.
求正三棱柱ABC-A1B1C1的体积.
迁移与应用
1.一个圆柱的侧面展开图是一个边长为4π的正方形,则这个圆柱的体积为__________.
2.根据图中物体的三视图(单位:cm),求此几何体体积.
名师点津
1.求柱体的体积关键是求其底面积和高,底面积利用平面图形面积的求法,常转化为三角形及四边形,高常与侧棱、斜高及其在底面的正投影组成直角三角形,进而求解.
2.求组合体的体积应据其结构特征分析求解,如迁移与应用题2中为长方体上放一圆柱,故几何体体积为两体积之和.
2.锥体的体积
活动与探究2
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=PD.
求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.
迁移与应用
1.一个圆锥的轴截面是边长为1的正三角形,则其体积为__________.
2.如图,ABCD-A1B1C1D1是棱长为6的正方体,点P,Q,R分别是棱AA1,AB,AD的中点,则三棱锥A-PQR的体积等于__________.
名师点津
(1)锥体的体积公式V=Sh既适合棱锥,也适合圆锥,其中棱锥可以是正棱锥,也可以不是正棱锥.
(2)三棱锥的体积求解具有较多的灵活性,因为三棱锥的任何一个面都可以作为底面,所以常常需要根据题目条件对其顶点和底面进行转换,这一方法叫做等积法.
3.台体的体积
活动与探究3
正四棱台的侧棱长为3
cm,两底面边长分别为1
cm和5
cm,求体积.
迁移与应用
四边形ABCD中,A(0,0),B(1,0),C(2,1),D(0,3),绕y轴旋转一周,求所得旋转体的体积.
名师点津
1.求台体的体积的一般方法是求出台体的上、下底面的面积和高,然后套用公式V=(S′++S)h计算求解.
2.由于台体可以看作是由一个平行于锥体底面的平面截去小锥体后剩余的部分,因此台体的体积也可以由大锥体的体积减去小锥体的体积来计算得到.
4.球的表面积和体积
活动与探究4
(1)设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( ).
A.3πa2
B.6πa2
C.12πa2
D.24πa2
(2)如果三个球的半径之比是1∶2∶3,那么最大球的体积是其余两个球的体积之和的( ).
A.1倍
B.2倍
C.3倍
D.4倍
迁移与应用
1.若一个球的体积为4π,则它的表面积为________.
2.如图是某几何体的三视图,则该几何体的体积为( ).
A.π+12
B.π+18
C.9π+42
D.36π+18
名师点津
计算球的表面积和体积时要注意的问题:
(1)关键是计算球的半径,而计算半径的关键是寻找球心的位置.因此,在解题过程中要特别关注题目中所揭示的球心位置,球面上的点等信息.
(2)当球的半径增加为原来的2倍时,球的表面积增加为原来的4倍,球的体积增加为原来的8倍.
(3)注意公式的“双向”应用,也就是说当知道球的表面积或体积时,也可以求出球的半径.
当堂检测
1.已知高为3的直三棱柱ABC-A′B′C′的底面是边长为1的正三角形,则三棱锥B′-ABC的体积为( ).
A.
B.
C.
D.
2.已知两个球的半径之比为1∶2,则这两个球的表面积之比为( ).
A.1∶2
B.1∶4
C.1∶6
D.1∶8
3.圆台的上、下底面的面积分别为π,4π,侧面积是6π,这个圆台的体积是( ).
A.
B.2π
C.
D.
4.将两个棱长为10
cm的正方体铜块熔化后铸成底面边长为5
cm的正四棱柱,则该四棱柱的高为( ).
A.8
cm
B.80
cm
C.40
cm
D.
cm
5.如图,一个底面直径为20
cm的装有一部分水的圆柱形玻璃杯,水中放着一个底面直径为6
cm,高为20
cm的一个圆锥形铅锤,当铅锤从水中取出后,杯里的水将下降几厘米?(π≈3.14)
盘点收获
提示:用最精练的语言把你当堂掌握的核心知识的精华部分和基本技能的要领部分写下来并进行识记.
答案:
课前预习导学
预习导引
预习交流1 提示:台体的体积公式中,如果S上=S下,就得到柱体的体积公式V柱体=Sh;如果S上=0,就得到锥体的体积公式V锥体=Sh.因此,柱体、锥体、台体的体积公式之间的关系,可表示如下.
由上图可见,柱体、锥体的体积公式是台体的体积公式的特例.
预习交流2 提示:体积相等,都等于Sh.
预习交流3 提示:V圆柱=πR2h,V圆锥=πR2h.
预习交流4 提示:表面积扩大为原来的4倍,体积扩大为原来的8倍.
课堂合作探究
问题导学
活动与探究1 思路分析:由三视图可以得到正三棱柱的底面三角形的高和侧棱长,从而可求出正三棱柱的底面边长与高,然后套用体积公式计算.
解:由三视图可知:在正三棱柱中,AD=,AA1=3,从而在底面即等边△ABC中,AB===2,所以正三棱柱的体积V=Sh=×BC×AD×AA1=×2××3=3.
迁移与应用 1.16π2 解析:设圆柱的底面半径为r,高为h,依题意有2πr=4π,h=4π,所以r=2,于是体积V=Sh=πr2h=π·22·4π=16π2.
2.解:该几何体上方是底面半径为,母线长为1的圆柱,下方是一个长、宽、高分别为4,1,1的长方体,
从而V=4×1×1+π·2·1=+4.
活动与探究2 思路分析:对于棱锥Q-ABCD,其底面为正方形ABCD,高即为QA,易求体积;对于三棱锥P-DCQ,若以△DCQ为底面,则应证明PQ是其高,然后再计算,也可将三角形CDP作为底面,这时其高易证即为AD,从而可求体积.
解:设AB=a.由题意知AQ即为棱锥Q-ABCD的高,
所以棱锥Q-ABCD的体积V1=Sh=×a2×a=a3.
方法1:由于棱锥P-DCQ与棱锥Q-CDP是同一个棱锥,其体积相等,
而其底面是Rt△CDP,面积为S1=×a×2a=a2.
取DP中点N,连接QN,则QN∥AD,
又AD⊥DC,AD⊥DP,
所以AD⊥平面CDP,
故QN⊥平面CDP.
因此QN就是三棱锥Q-CDP的高,且QN=AD=a.
于是棱锥P-DCQ的体积V2=VQ-CDP=×a×a2=a3.
于是V1∶V2=1.
方法2:因为QA⊥平面ABCD,
所以平面PDAQ⊥平面ABCD,交线为AD.
又四边形ABCD为正方形,DC⊥AD,
所以DC⊥平面PDAQ.于是得PQ⊥DC.
在直角梯形PDAQ中,可得DQ=PQ=PD,则PQ⊥QD,所以PQ⊥平面DCQ.
即PQ为三棱锥P-DCQ的高,且PQ=a,
而△DCQ的面积为·a·a=a2,
所以三棱锥P-DCQ的体积V2=·a2·a=a3,
于是V1∶V2=1.
迁移与应用 1.π 解析:依题意,圆锥的底面半径为,高为,于是体积V=π·2·=π.
2. 解析:VA-PQR=VQ-APR=S△APR·AQ=××3×3×3=.
活动与探究3 思路分析:解答本题的关键是利用侧棱与高构成的直角梯形求出台体的高,进而求出正四棱台的体积.
解:正四棱台ABCD-A1B1C1D1中O1,O分别是两底面的中心.
∵A1C1=,AC=5,
∴A1O1=,AO=,
∴O1O==1,
V=×1×(12+52+)
=(1+25+5)=(cm3).
迁移与应用 解:∵C(2,1),D(0,3),
∴圆锥的底面半径r=2,高h=2.
∴V圆锥=πr2h=π×22×2=π.
∵B(1,0),C(2,1),
∴圆台的两个底面半径R=2,R′=1,高h′=1.
∴V圆台=πh′(R2+R′2+RR′)
=π×1×(22+12+2×1)=π,
∴V=V圆锥+V圆台=5π.
活动与探究4 思路分析:(1)该球的直径等于长方体的体对角线长.
(2)可设出球的半径,计算出三个球的体积,然后求得结论.
(1)B
(2)C 解析:(1)由于长方体的长、宽、高分别为2a,a,a,则长方体的体对角线长为=a.又长方体外接球的直径2R等于长方体的体对角线,∴2R=a.
∴S球=4πR2=6πa2.
(2)半径大的球的体积也大,设三个球的半径分别为x,2x,3x,则最大球的半径为3x,其体积为π×(3x)3,其余两个球的体积之和为πx3+π×(2x)3,
∴π×(3x)3÷=3.
迁移与应用 1.12π 解析:设球的半径为
R,由R3=4π,得R=,所以S=4πR2=12π.
2.B 解析:由题意知该几何体上部为直径为3的球,下部为长、宽、高分别为3,3,2的长方体,∴该几何体的体积为V=π×2+3×3×2=+18.
当堂检测
1.D 2.B 3.D 4.B
5.解:设水面下降的高度为x
cm,因为圆锥形铅锤的体积为×π×2×20=60π(cm3),
小圆柱的体积为π×(20÷2)2×x=100πx(cm3).
所以60π=100πx,解得x=0.6(cm).则铅锤取出后,杯中水面下降了0.6
cm.
