2.3.1 空间直角坐标系的建立 同步练习(含答案)
文档属性
| 名称 | 2.3.1 空间直角坐标系的建立 同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 00:00:00 | ||
图片预览

文档简介
2.3.1
空间直角坐标系的建立
同步练习
课后训练
1.点M所在的位置是( ).
A.x轴上
B.xOz平面内
C.xOy平面内
D.yOz平面内
2.xOy平面内点的坐标的特点是( ).
A.z坐标是0
B.x坐标和y坐标都是0
C.x坐标是0
D.x坐标,y坐标和z坐标不可能都是0
3.在空间直角坐标系中,点P(1,3,-5)关于xOz平面对称的点的坐标是( ).
A.(-1,3,-5)
B.(1,-3,5)
C.
(1,-3,-5)
D.(-1,-3,5)
4.在空间直角坐标系中,已知点P(1,,),过P作yOz平面的垂线PQ,则垂足Q的坐标是( ).
A.(0,,0)
B.(0,,)
C.(1,0,)
D.(1,
,0)
5.在空间直角坐标系中,已知M(-1,2,3),过该点作x轴的垂线,垂足为H,则H点的坐标是( ).
A.(-1,2,0)
B.(-1,0,3)
C.(-1,0,0)
D.(0,2,3)
6.设x为任意实数,相应的点(3,x,3)的集合是( ).
A.一个平行于y轴的平面
B.一条平行于y轴的直线
C.一个垂直于y轴的平面
D.一条垂直于y轴的直线
7.点P(-4,2,-3)关于xOy平面的对称点是________;关于yOz平面的对称点是________;关于xOz平面的对称点是________;关于x轴的对称点是________;关于y轴的对称点是________;关于z轴的对称点是________.
8.如图,以棱长为1的正方体ABCD-A1B1C1D1的棱AD,AB,AA1所在直线为坐标轴,建立空间直角坐标系,则面AA1B1B对角线的交点的坐标为__________.
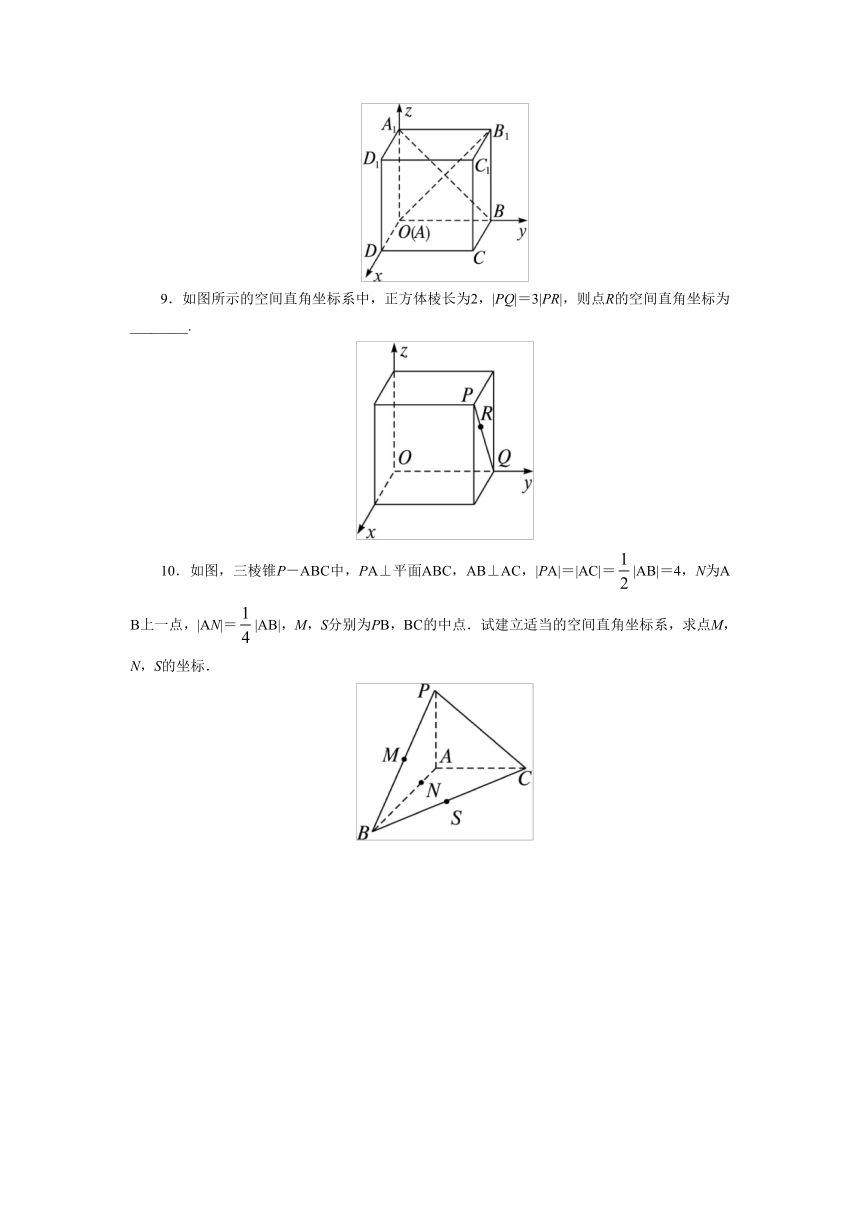
9.如图所示的空间直角坐标系中,正方体棱长为2,|PQ|=3|PR|,则点R的空间直角坐标为________.
10.如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,|PA|=|AC|=|AB|=4,N为AB上一点,|AN|=|AB|,M,S分别为PB,BC的中点.试建立适当的空间直角坐标系,求点M,N,S的坐标.
参考答案
1答案:D
2答案:A
3答案:C
4答案:B 解析:根据空间直角坐标系的概念知yOz平面上的点Q的x坐标为0,y坐标,z坐标分别等于点P的y坐标,z坐标,∴垂足Q的坐标为(0,,).
5答案:C 解析:因为垂足H在x轴上,故点H与M的x坐标相等,其余两个坐标均为0.
6答案:B
7答案:(-4,2,3) (4,2,-3) (-4,-2,-3) (-4,-2,3) (4,2,3) (4,-2,-3)
8答案:
9答案: 解析:设P,R在xOy面上的射影分别是S,M,过M作MN⊥x轴.
由于△QRM∽△QPS,
则,可得,,
因此R点坐标为.
10答案:解:由线面垂直的性质可知AB,AC,AP三条直线两两垂直,如图,分别以AB,AC,AP所在直线为x轴,y轴,z轴建立空间直角坐标系,则B(8,0,0),C(0,4,0),P(0,0,4),因为M,S分别为PB,BC的中点,由中点坐标公式可得,M(4,0,2),S(4,2,0).因为N在x轴上,|AN|=2,
所以N(2,0,0).
空间直角坐标系的建立
同步练习
课后训练
1.点M所在的位置是( ).
A.x轴上
B.xOz平面内
C.xOy平面内
D.yOz平面内
2.xOy平面内点的坐标的特点是( ).
A.z坐标是0
B.x坐标和y坐标都是0
C.x坐标是0
D.x坐标,y坐标和z坐标不可能都是0
3.在空间直角坐标系中,点P(1,3,-5)关于xOz平面对称的点的坐标是( ).
A.(-1,3,-5)
B.(1,-3,5)
C.
(1,-3,-5)
D.(-1,-3,5)
4.在空间直角坐标系中,已知点P(1,,),过P作yOz平面的垂线PQ,则垂足Q的坐标是( ).
A.(0,,0)
B.(0,,)
C.(1,0,)
D.(1,
,0)
5.在空间直角坐标系中,已知M(-1,2,3),过该点作x轴的垂线,垂足为H,则H点的坐标是( ).
A.(-1,2,0)
B.(-1,0,3)
C.(-1,0,0)
D.(0,2,3)
6.设x为任意实数,相应的点(3,x,3)的集合是( ).
A.一个平行于y轴的平面
B.一条平行于y轴的直线
C.一个垂直于y轴的平面
D.一条垂直于y轴的直线
7.点P(-4,2,-3)关于xOy平面的对称点是________;关于yOz平面的对称点是________;关于xOz平面的对称点是________;关于x轴的对称点是________;关于y轴的对称点是________;关于z轴的对称点是________.
8.如图,以棱长为1的正方体ABCD-A1B1C1D1的棱AD,AB,AA1所在直线为坐标轴,建立空间直角坐标系,则面AA1B1B对角线的交点的坐标为__________.
9.如图所示的空间直角坐标系中,正方体棱长为2,|PQ|=3|PR|,则点R的空间直角坐标为________.
10.如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,|PA|=|AC|=|AB|=4,N为AB上一点,|AN|=|AB|,M,S分别为PB,BC的中点.试建立适当的空间直角坐标系,求点M,N,S的坐标.
参考答案
1答案:D
2答案:A
3答案:C
4答案:B 解析:根据空间直角坐标系的概念知yOz平面上的点Q的x坐标为0,y坐标,z坐标分别等于点P的y坐标,z坐标,∴垂足Q的坐标为(0,,).
5答案:C 解析:因为垂足H在x轴上,故点H与M的x坐标相等,其余两个坐标均为0.
6答案:B
7答案:(-4,2,3) (4,2,-3) (-4,-2,-3) (-4,-2,3) (4,2,3) (4,-2,-3)
8答案:
9答案: 解析:设P,R在xOy面上的射影分别是S,M,过M作MN⊥x轴.
由于△QRM∽△QPS,
则,可得,,
因此R点坐标为.
10答案:解:由线面垂直的性质可知AB,AC,AP三条直线两两垂直,如图,分别以AB,AC,AP所在直线为x轴,y轴,z轴建立空间直角坐标系,则B(8,0,0),C(0,4,0),P(0,0,4),因为M,S分别为PB,BC的中点,由中点坐标公式可得,M(4,0,2),S(4,2,0).因为N在x轴上,|AN|=2,
所以N(2,0,0).
