2.3.1-2.3.2 空间直角坐标系的建立和空间直角坐标系中点的坐标 同步练习2(含答案)
文档属性
| 名称 | 2.3.1-2.3.2 空间直角坐标系的建立和空间直角坐标系中点的坐标 同步练习2(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 201.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 18:57:15 | ||
图片预览

文档简介
2.3.1-2.3.2
空间直角坐标系的建立和空间直角坐标系中点的坐标
同步练习
一、选择题(每小题4分,共16分)
1.点A(-3,0,0)位于(
)
(A)x轴上
(B)y轴上
(C)xOz平面内
(D)xOy平面内
2.点P(-3,6,-
2)与Q(3,6,-2)的位置关系为
(
)
(A)关于x轴对称
(B)关于y轴对称
(C)关于yOz平面对称
(D)关于xOz平面对称
3.点A(-1,
,2)在xOz平面的投影点的坐标为(
)
(A)(-1,
-,
2)
(B)(-1,
0,
2)
(C)(1,
,
-2)
(D)(0,
,
0)
4.以正方体ABCD-A1B1C1D1的棱AB,AD,AA1所在的直线为坐标轴建立空间直角坐标系,且正方体的棱长为一个单位长度,则棱CC1中点坐标为(
)
(A)(,1,1)
(B)(1,,1)
(C)(1,1,)
(D)(,,1)
二、填空题(每小题4分,共8分)
5.在空间直角坐标系中,点P(1,2,3)关于yOz平面的对称点的坐标是__________.
6.空间直角坐标系中,点A(a,3,4)和点B(-1,b,c)关于点C(1,-3,2)对称,则a+b+c=_________.
三、解答题(每小题8分,共16分)
7.如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标是(),点D在平面yOz上,且∠BDC=90°,∠DCB=30°,求点D的坐标.
8.(易错题)如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,|PA|=|AC|=|AB|=4,N为AB上一点,|AN|=|AB|,M,S分别为PB,BC的中点.试建立适当的空间直角坐标系,求点M,N,S的坐标.
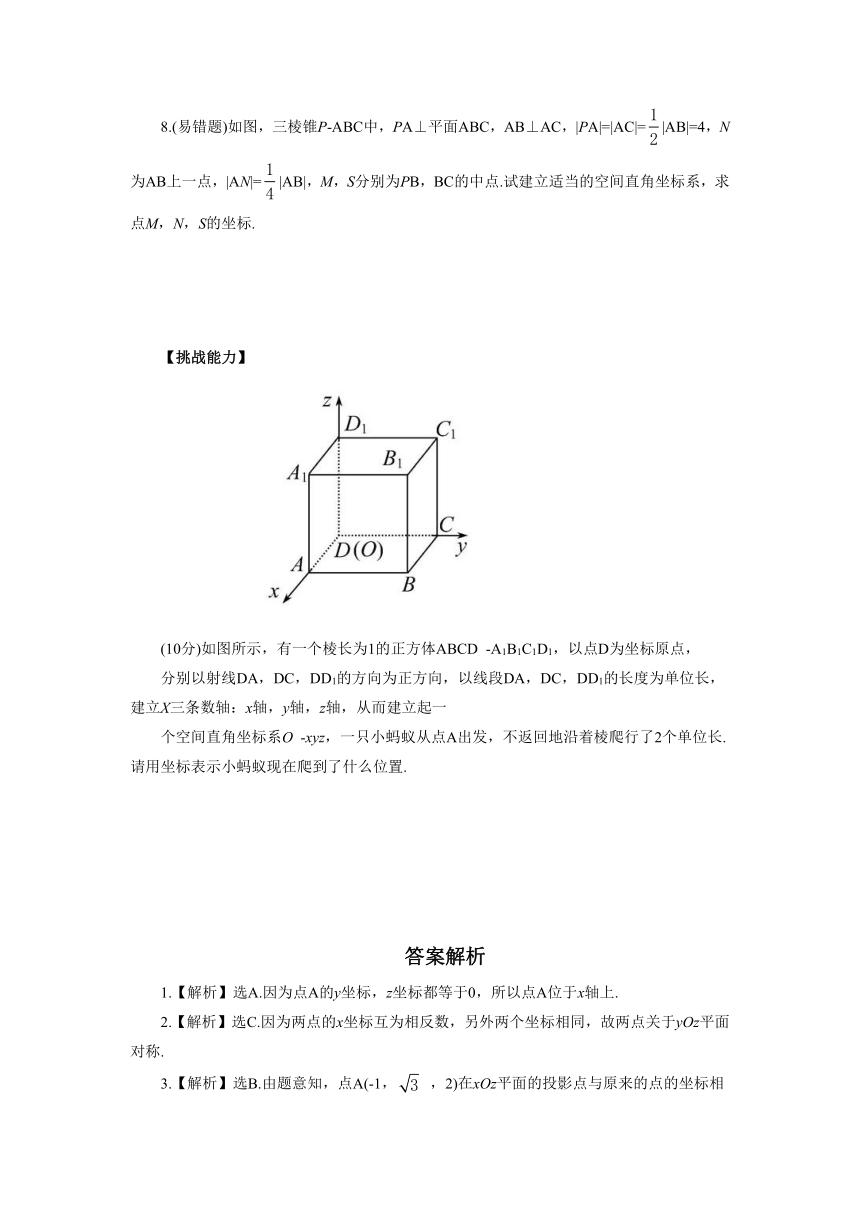
【挑战能力】
(10分)如图所示,有一个棱长为1的正方体ABCD
-A1B1C1D1,以点D为坐标原点,
分别以射线DA,DC,DD1的方向为正方向,以线段DA,DC,DD1的长度为单位长,建立X三条数轴:x轴,y轴,z轴,从而建立起一
个空间直角坐标系O
-xyz,一只小蚂蚁从点A出发,不返回地沿着棱爬行了2个单位长.请用坐标表示小蚂蚁现在爬到了什么位置.
答案解析
1.【解析】选A.因为点A的y坐标,z坐标都等于0,所以点A位于x轴上.
2.【解析】选C.因为两点的x坐标互为相反数,另外两个坐标相同,故两点关于yOz平面对称.
3.【解析】选B.由题意知,点A(-1,
,2)在xOz平面的投影点与原来的点的坐标相比,x坐标与z坐标不变,y坐标变为0.故选B.
4.【解题指南】先写出点C,C1的坐标,然后利用中点坐标公式求解即可.
【解析】选C.由题可知点C(1,1,0),C1(1,1,1),
∴棱CC1中点坐标为(1,1,).
5.【解析】点关于yOz平面的对称点的坐标只需让x坐标变为原来的相反数,y,z坐标不变,故P(1,2,3)关于yOz平面的对称点的坐标为(1,-2,-
3).
答案:(-1,2,3)
【变式训练】求点P(1,2,3)关于x轴的对称点的坐标.
【解析】点关于x轴的对称点的坐标只需保持x坐标不变,y,z坐标变为原来的相反数即可,故点P(1,2,3)关于x轴的对称点的坐标为(1,-2,-3).
6.【解析】由中点坐标公式,得
故a+b+c=-6.
答案:-6
7.【解析】过点D作DE⊥BC,垂足为E.
在Rt△BCD中,由∠BDC=90°,
∠DCB=30°,BC=2,得BD=1,CD=,
∴DE=CDsin30°=,
OE=OB-BE=OB-BDcos60°=1-=,
∴点D的坐标为(0,-,).
8.【解析】由线面垂直的性质可知AB,AC,AP三条直线两两垂直,
如图,分别以AB,AC,AP所在直线为x轴,y轴,
z轴建立空间直角坐标系,则B(8,0,0),
C(0,4,0),P(0,0,4).因为M,
S分别为PB,BC的中点,由中点坐标公式可
得,M(4,0,2),S(4,2,0).因为N在
x轴上,|AN|=2,所以N(2,0,
0).
【方法技巧】巧建坐标系轻松解题
(1)建立空间直角坐标系时,要考虑如何建系才能使点的坐标简单,便于计算,一般是要使尽量多的点在坐标轴上.
(2)对长方体或正方体,一般取相邻的三条棱所在直线为x,y,z轴建立空间直角坐标系;确定点的坐标时,最常用的方法就是求某些与轴平行的线段的长度,即将坐标转化为与轴平行的线段长度,同时要注意坐标的符号,这也是求空间点的坐标的关键.
【挑战能力】
【解题指南】小蚂蚁爬行的方向不同,位置也不同,故要分类讨论.
【解析】小蚂蚁由点A出发可从六条路线中任选一条前进,最后到达点C或点B1或点D1中某一个点的位置.
小蚂蚁沿着A-B-C或A-B-B1或A-D-C或A-D-D1或A-A1-B1或A-A1-D1任一条路线爬行,其终点为点C或B1或D1.点C在y轴上,且DC=1,则其纵坐标为1,横坐标与竖坐标均为0,所以点C的坐标是(0,1,0);点B1在xOy平面上的投影是点B,点B在xOy平面上的坐标是(1,1,0),且|B1B|=1,则B1的竖坐标为1,所以点B1的坐标是(1,1,1);仿照点C的求法,可知点D1的坐标是(0,0,1).
空间直角坐标系的建立和空间直角坐标系中点的坐标
同步练习
一、选择题(每小题4分,共16分)
1.点A(-3,0,0)位于(
)
(A)x轴上
(B)y轴上
(C)xOz平面内
(D)xOy平面内
2.点P(-3,6,-
2)与Q(3,6,-2)的位置关系为
(
)
(A)关于x轴对称
(B)关于y轴对称
(C)关于yOz平面对称
(D)关于xOz平面对称
3.点A(-1,
,2)在xOz平面的投影点的坐标为(
)
(A)(-1,
-,
2)
(B)(-1,
0,
2)
(C)(1,
,
-2)
(D)(0,
,
0)
4.以正方体ABCD-A1B1C1D1的棱AB,AD,AA1所在的直线为坐标轴建立空间直角坐标系,且正方体的棱长为一个单位长度,则棱CC1中点坐标为(
)
(A)(,1,1)
(B)(1,,1)
(C)(1,1,)
(D)(,,1)
二、填空题(每小题4分,共8分)
5.在空间直角坐标系中,点P(1,2,3)关于yOz平面的对称点的坐标是__________.
6.空间直角坐标系中,点A(a,3,4)和点B(-1,b,c)关于点C(1,-3,2)对称,则a+b+c=_________.
三、解答题(每小题8分,共16分)
7.如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标是(),点D在平面yOz上,且∠BDC=90°,∠DCB=30°,求点D的坐标.
8.(易错题)如图,三棱锥P-ABC中,PA⊥平面ABC,AB⊥AC,|PA|=|AC|=|AB|=4,N为AB上一点,|AN|=|AB|,M,S分别为PB,BC的中点.试建立适当的空间直角坐标系,求点M,N,S的坐标.
【挑战能力】
(10分)如图所示,有一个棱长为1的正方体ABCD
-A1B1C1D1,以点D为坐标原点,
分别以射线DA,DC,DD1的方向为正方向,以线段DA,DC,DD1的长度为单位长,建立X三条数轴:x轴,y轴,z轴,从而建立起一
个空间直角坐标系O
-xyz,一只小蚂蚁从点A出发,不返回地沿着棱爬行了2个单位长.请用坐标表示小蚂蚁现在爬到了什么位置.
答案解析
1.【解析】选A.因为点A的y坐标,z坐标都等于0,所以点A位于x轴上.
2.【解析】选C.因为两点的x坐标互为相反数,另外两个坐标相同,故两点关于yOz平面对称.
3.【解析】选B.由题意知,点A(-1,
,2)在xOz平面的投影点与原来的点的坐标相比,x坐标与z坐标不变,y坐标变为0.故选B.
4.【解题指南】先写出点C,C1的坐标,然后利用中点坐标公式求解即可.
【解析】选C.由题可知点C(1,1,0),C1(1,1,1),
∴棱CC1中点坐标为(1,1,).
5.【解析】点关于yOz平面的对称点的坐标只需让x坐标变为原来的相反数,y,z坐标不变,故P(1,2,3)关于yOz平面的对称点的坐标为(1,-2,-
3).
答案:(-1,2,3)
【变式训练】求点P(1,2,3)关于x轴的对称点的坐标.
【解析】点关于x轴的对称点的坐标只需保持x坐标不变,y,z坐标变为原来的相反数即可,故点P(1,2,3)关于x轴的对称点的坐标为(1,-2,-3).
6.【解析】由中点坐标公式,得
故a+b+c=-6.
答案:-6
7.【解析】过点D作DE⊥BC,垂足为E.
在Rt△BCD中,由∠BDC=90°,
∠DCB=30°,BC=2,得BD=1,CD=,
∴DE=CDsin30°=,
OE=OB-BE=OB-BDcos60°=1-=,
∴点D的坐标为(0,-,).
8.【解析】由线面垂直的性质可知AB,AC,AP三条直线两两垂直,
如图,分别以AB,AC,AP所在直线为x轴,y轴,
z轴建立空间直角坐标系,则B(8,0,0),
C(0,4,0),P(0,0,4).因为M,
S分别为PB,BC的中点,由中点坐标公式可
得,M(4,0,2),S(4,2,0).因为N在
x轴上,|AN|=2,所以N(2,0,
0).
【方法技巧】巧建坐标系轻松解题
(1)建立空间直角坐标系时,要考虑如何建系才能使点的坐标简单,便于计算,一般是要使尽量多的点在坐标轴上.
(2)对长方体或正方体,一般取相邻的三条棱所在直线为x,y,z轴建立空间直角坐标系;确定点的坐标时,最常用的方法就是求某些与轴平行的线段的长度,即将坐标转化为与轴平行的线段长度,同时要注意坐标的符号,这也是求空间点的坐标的关键.
【挑战能力】
【解题指南】小蚂蚁爬行的方向不同,位置也不同,故要分类讨论.
【解析】小蚂蚁由点A出发可从六条路线中任选一条前进,最后到达点C或点B1或点D1中某一个点的位置.
小蚂蚁沿着A-B-C或A-B-B1或A-D-C或A-D-D1或A-A1-B1或A-A1-D1任一条路线爬行,其终点为点C或B1或D1.点C在y轴上,且DC=1,则其纵坐标为1,横坐标与竖坐标均为0,所以点C的坐标是(0,1,0);点B1在xOy平面上的投影是点B,点B在xOy平面上的坐标是(1,1,0),且|B1B|=1,则B1的竖坐标为1,所以点B1的坐标是(1,1,1);仿照点C的求法,可知点D1的坐标是(0,0,1).
