2.3.3 空间两点间的距离公式 同步练习1(含答案)
文档属性
| 名称 | 2.3.3 空间两点间的距离公式 同步练习1(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 293.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-23 19:01:14 | ||
图片预览

文档简介
2.3.3
空间两点间的距离公式
同步练习
一、选择题(每小题4分,共16分)
1.点A(3,5,-6)在z轴上的投影为B,则|AB|=(
)
(A)5
(B)6
(C)
(D)
2.点P(x,2,1)到Q(1,1,2),R(2,1,1)的距离相等,则x=(
)
(A)
(B)1
(C)
(D)2
3.设A(3,3,1),B(1,0,5),C(0,1,0),则AB中点M到点C的距离为(
)
(A)
(B)
(C)
(D)
4.在空间直角坐标系中,正方体ABCD
-A1B1C1D1的顶点A(3,-1,2),其中心M的坐标为(0,1,2),则该正方体的棱长为(
)
(A)10
(B)
(C)
(D)
二、填空题(每小题4分,共8分)
5.在空间直角坐标系O-xyz中,满足条件x2+y2+z2≤1的点(x,y,z)构成的空间区域的体积为V,则V=________.
6.(易错题)点M(4,-3,5)到x轴的距离为m,到xOy平面的距离为n,则m2+n=
_________.
三、解答题(每小题8分,共16分)
7.如图所示,正方体ABCD-A′B′C′D′的棱长为a,P,Q分别是D′B,B′C的中点,求PQ的长.
8.如图,正方形ABCD,ABEF的边长都是1,
且平面ABCD,ABEF互相垂直,点M在AC上移
动,点N在BF上移动,若CM=BN=a(0<a<).
(1)求MN的长;
(2)当a为何值时,MN的长最小.
【挑战能力】
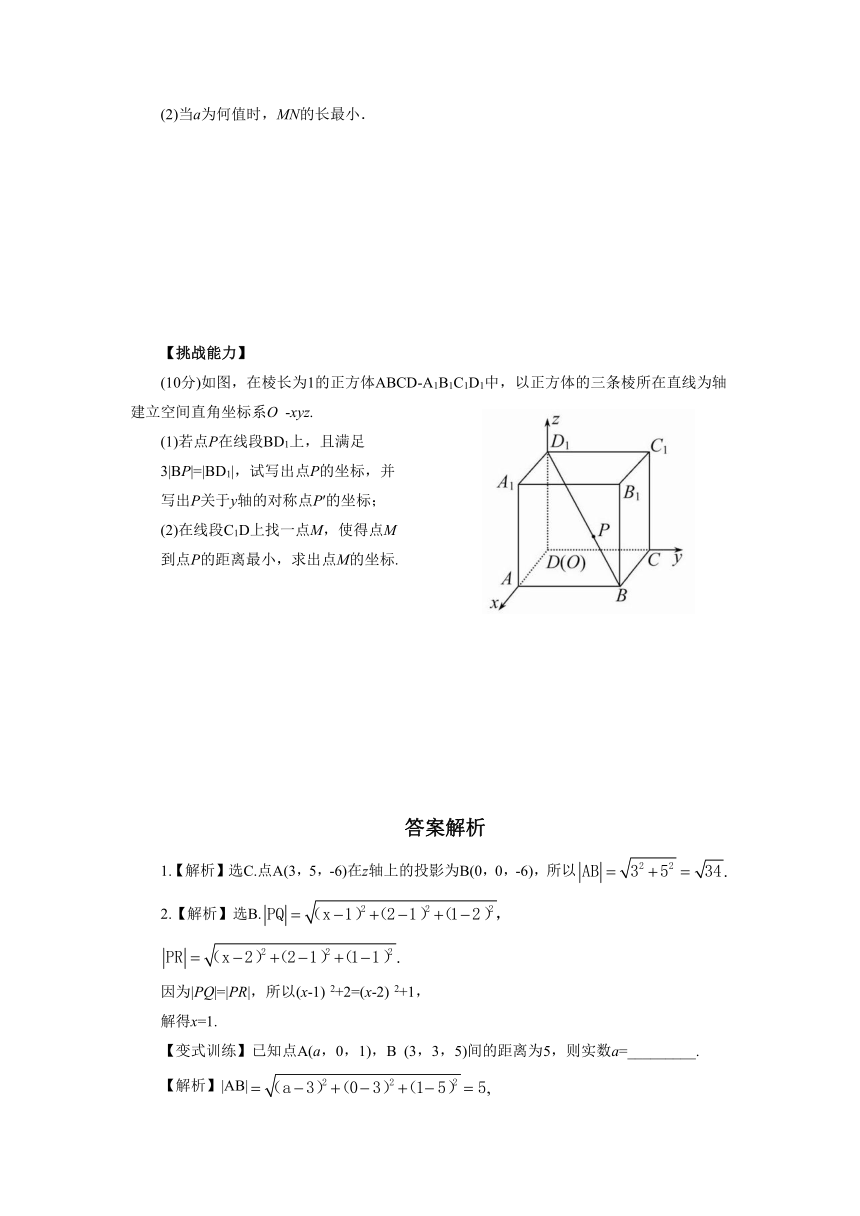
(10分)如图,在棱长为1的正方体ABCD-A1B1C1D1中,以正方体的三条棱所在直线为轴建立空间直角坐标系O
-xyz.
(1)若点P在线段BD1上,且满足
3|BP|=|BD1|,试写出点P的坐标,并
写出P关于y轴的对称点P′的坐标;
(2)在线段C1D上找一点M,使得点M
到点P的距离最小,求出点M的坐标.
答案解析
1.【解析】选C.点A(3,5,-6)在z轴上的投影为B(0,0,-6),所以
2.【解析】选B.
因为|PQ|=|PR|,所以(x-1)
2+2=(x-2)
2+1,
解得x=1.
【变式训练】已知点A(a,0,1),B
(3,3,5)间的距离为5,则实数a=_________.
【解析】|AB|
解得a=3.
答案:3
3.【解析】选C.由中点坐标公式可得M(2,,3),再由两点间的距离公式可得
4.【解析】选B.由A(3,-1,2),中心M(0,1,2),所以C1(-3,
3,2).正方体的对角线长为AC1=
所以正方体棱长为
5.【解析】由题意知,
满足条件x2+y2+z2≤1的点(x,y,z)构成的空间区域为半径为1的一个球,V=π.
答案:
π
6.【解析】由题意n=5,
所以m2+n=34+5=39.
答案:39
【误区警示】解决此类问题容易把点到坐标轴的距离与点到坐标平面的距离混淆,导致出现计算错误.
7.【解析】以D为坐标原点,DA,DC,DD′分别为x轴,y轴,z轴建立空间直角坐标系,由题意得,B(a,a,0),
D′(0,0,a),
∴P(,,).
又∵C(0,a,0),B′(a,a,a),
∴Q(,a,
).
∴|PQ|=
8.【解析】(1)如图,以点B为原点,BA,BE,BC所在直线分别为x轴,y轴,
z轴,建立空间直角坐标系.
可求得M(),
N().
∴
(2)由(1)知
∴当时,|MN|=
,即M,N分别移动到AC,BF的中点时,MN的长最小,最小值为.
【挑战能力】
【解题指南】第(1)问借助3|BP|=|BD1|及平面几何的知识求点P的坐标,利用对称关系求点P′的坐标;第(2)问利用空间两点间的距离公式建立点M到点P的距离的函数,并用函数的思想求其最小值,即此时的点M的坐标.
【解析】(1)由题意知P的坐标为(),
P关于y轴的对称点P′的坐标为().
(2)设线段C1D上一点M的坐标为(0,m,m),则有
当m=时|MP|取到最小值,
所以点M为(0,,).
空间两点间的距离公式
同步练习
一、选择题(每小题4分,共16分)
1.点A(3,5,-6)在z轴上的投影为B,则|AB|=(
)
(A)5
(B)6
(C)
(D)
2.点P(x,2,1)到Q(1,1,2),R(2,1,1)的距离相等,则x=(
)
(A)
(B)1
(C)
(D)2
3.设A(3,3,1),B(1,0,5),C(0,1,0),则AB中点M到点C的距离为(
)
(A)
(B)
(C)
(D)
4.在空间直角坐标系中,正方体ABCD
-A1B1C1D1的顶点A(3,-1,2),其中心M的坐标为(0,1,2),则该正方体的棱长为(
)
(A)10
(B)
(C)
(D)
二、填空题(每小题4分,共8分)
5.在空间直角坐标系O-xyz中,满足条件x2+y2+z2≤1的点(x,y,z)构成的空间区域的体积为V,则V=________.
6.(易错题)点M(4,-3,5)到x轴的距离为m,到xOy平面的距离为n,则m2+n=
_________.
三、解答题(每小题8分,共16分)
7.如图所示,正方体ABCD-A′B′C′D′的棱长为a,P,Q分别是D′B,B′C的中点,求PQ的长.
8.如图,正方形ABCD,ABEF的边长都是1,
且平面ABCD,ABEF互相垂直,点M在AC上移
动,点N在BF上移动,若CM=BN=a(0<a<).
(1)求MN的长;
(2)当a为何值时,MN的长最小.
【挑战能力】
(10分)如图,在棱长为1的正方体ABCD-A1B1C1D1中,以正方体的三条棱所在直线为轴建立空间直角坐标系O
-xyz.
(1)若点P在线段BD1上,且满足
3|BP|=|BD1|,试写出点P的坐标,并
写出P关于y轴的对称点P′的坐标;
(2)在线段C1D上找一点M,使得点M
到点P的距离最小,求出点M的坐标.
答案解析
1.【解析】选C.点A(3,5,-6)在z轴上的投影为B(0,0,-6),所以
2.【解析】选B.
因为|PQ|=|PR|,所以(x-1)
2+2=(x-2)
2+1,
解得x=1.
【变式训练】已知点A(a,0,1),B
(3,3,5)间的距离为5,则实数a=_________.
【解析】|AB|
解得a=3.
答案:3
3.【解析】选C.由中点坐标公式可得M(2,,3),再由两点间的距离公式可得
4.【解析】选B.由A(3,-1,2),中心M(0,1,2),所以C1(-3,
3,2).正方体的对角线长为AC1=
所以正方体棱长为
5.【解析】由题意知,
满足条件x2+y2+z2≤1的点(x,y,z)构成的空间区域为半径为1的一个球,V=π.
答案:
π
6.【解析】由题意n=5,
所以m2+n=34+5=39.
答案:39
【误区警示】解决此类问题容易把点到坐标轴的距离与点到坐标平面的距离混淆,导致出现计算错误.
7.【解析】以D为坐标原点,DA,DC,DD′分别为x轴,y轴,z轴建立空间直角坐标系,由题意得,B(a,a,0),
D′(0,0,a),
∴P(,,).
又∵C(0,a,0),B′(a,a,a),
∴Q(,a,
).
∴|PQ|=
8.【解析】(1)如图,以点B为原点,BA,BE,BC所在直线分别为x轴,y轴,
z轴,建立空间直角坐标系.
可求得M(),
N().
∴
(2)由(1)知
∴当时,|MN|=
,即M,N分别移动到AC,BF的中点时,MN的长最小,最小值为.
【挑战能力】
【解题指南】第(1)问借助3|BP|=|BD1|及平面几何的知识求点P的坐标,利用对称关系求点P′的坐标;第(2)问利用空间两点间的距离公式建立点M到点P的距离的函数,并用函数的思想求其最小值,即此时的点M的坐标.
【解析】(1)由题意知P的坐标为(),
P关于y轴的对称点P′的坐标为().
(2)设线段C1D上一点M的坐标为(0,m,m),则有
当m=时|MP|取到最小值,
所以点M为(0,,).
