3.6直线和圆的关系(第二课时)优质课件(共18张PPT)
文档属性
| 名称 | 3.6直线和圆的关系(第二课时)优质课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-25 14:15:55 | ||
图片预览





文档简介
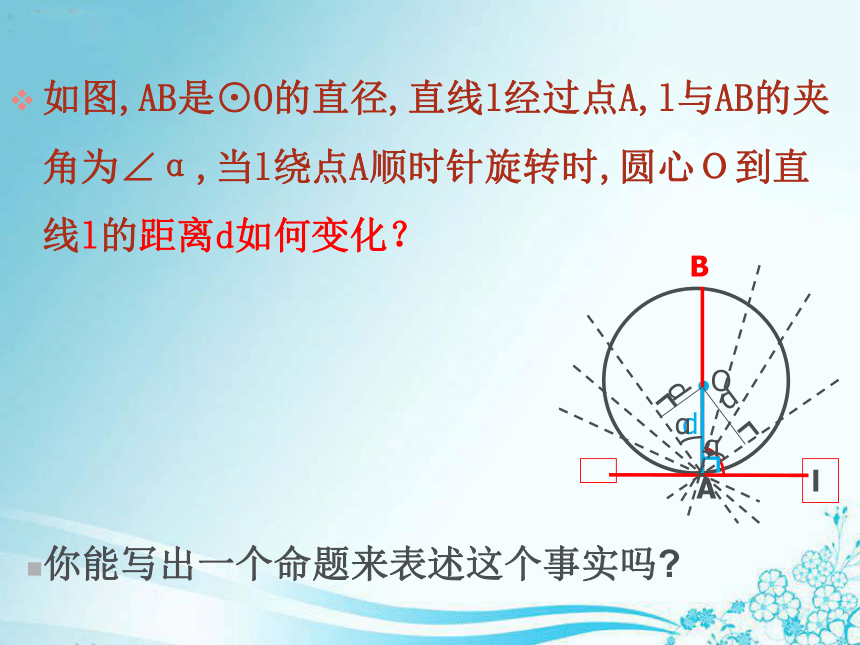
课件18张PPT。北师大版九年级下册第三章《圆》 3.6直线和圆的位置关系(第二课时)直线和圆相交d rd r 直线和圆相切直线和圆相离d r●O相交相切 相离┐dd┐d┐<=>如图,AB是⊙O的直径,直线l经过点A,l与AB的夹角为∠α,当l绕点A顺时针旋转时,圆心O到直线l的距离d如何变化?
你能写出一个命题来表述这个事实吗?经过直径的一端,并且垂直于这条直径的直线是圆的切线.∵AB是⊙O的直径,直线CD经过A点,且CD⊥AB,
∴ CD是⊙O的切线.这个定理实际上就是:
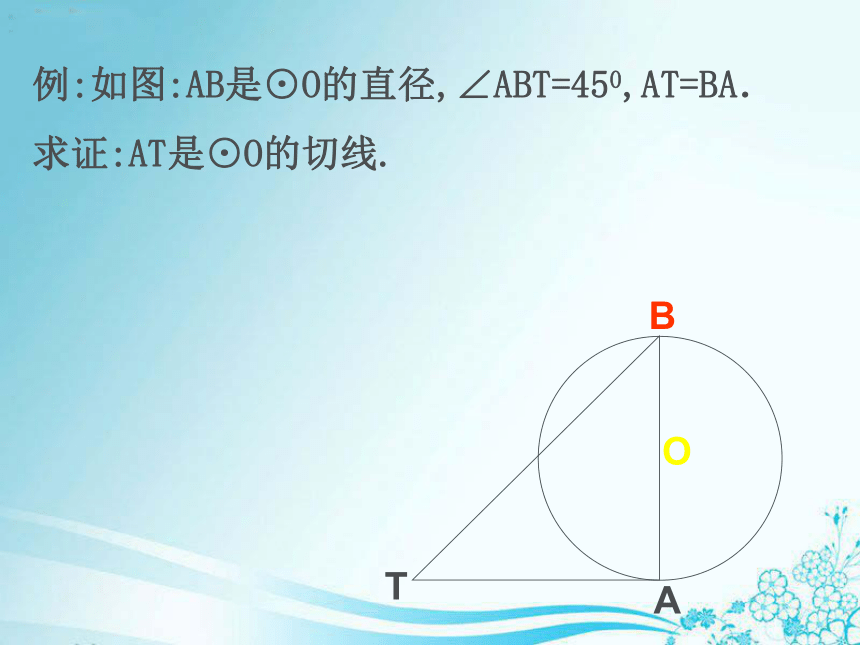
d=r 直线和圆相切的另一种说法。例:如图:AB是⊙O的直径,∠ABT=450,AT=BA.
求证:AT是⊙O的切线. 1.如图,已知直线AB 经过⊙O 上的点C, 并且OA=OB,CA=CB,那么直线 AB是⊙O 的切线吗? OAB1.由定理可知:经过三角形三个顶点可以作一个圆。
2.经过三角形各顶点的圆叫做
三角形的外接圆。
3.三角形外接圆的圆心叫做
三角形的外心,这个三角形叫做这个圆的内接三角形。三角形与圆的位置关系(回顾)探索:从一块三角形材料中,能否剪下一个圆,使其与各边都相切?I●I●上右图就是三角形的内切圆作法:D (1)作∠ABC、∠ACB的平分线BM和CN,交点为I.
(2)过点I作ID⊥BC,垂足为D.
(3)以I为圆心,ID为半径作⊙I, ⊙I就是所求MN这样的圆可以作出几个呢?为什么?∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),因此和△ABC三边都相切的圆可以作出一个,并且只能作一个. 定义:
与三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点. 分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?提示:先确定圆心和半径,尺规作图要保留作图痕迹. 判断题:
1.三角形的内心到三角形各个顶点的距离相等。( )
2.三角形的外心到三角形各边的距离相等。( )
3.等边三角形的内心和外心重( )错错对4、三角形的内心一定在三角形的内部( )
5、菱形一定有内切圆( )
6、矩形一定有内切圆( )
对 错 对
例2:如图,在△ABC中,点O是内心,
(1)若∠ABC=50°,∠ACB=70°,求∠BOC的度数(2)若∠A=80度,则∠BOC=
(3)若∠BOC=110度,则∠A= 130401。已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,∠AC=3,BC=4.
求⊙O的半径r. ABC●┏O Rt△的三边长与其内切圆半径间的关系bac已知:如图,△ABC的面积S=4cm2,周长等于10cm.
求内切圆⊙O的半径r.斜△的三边长及面积与其内切圆半径间的关系思考题:
如图,某乡镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑,以树立起文明古镇的形象。已知雕塑中心M到道路三边AC、BC、AB的距离相等,AC⊥BC,BC=30米,AC=40米。请你帮助计算一下,镇标雕塑中心M离道路三边的距离有多远?谢谢
你能写出一个命题来表述这个事实吗?经过直径的一端,并且垂直于这条直径的直线是圆的切线.∵AB是⊙O的直径,直线CD经过A点,且CD⊥AB,
∴ CD是⊙O的切线.这个定理实际上就是:
d=r 直线和圆相切的另一种说法。例:如图:AB是⊙O的直径,∠ABT=450,AT=BA.
求证:AT是⊙O的切线. 1.如图,已知直线AB 经过⊙O 上的点C, 并且OA=OB,CA=CB,那么直线 AB是⊙O 的切线吗? OAB1.由定理可知:经过三角形三个顶点可以作一个圆。
2.经过三角形各顶点的圆叫做
三角形的外接圆。
3.三角形外接圆的圆心叫做
三角形的外心,这个三角形叫做这个圆的内接三角形。三角形与圆的位置关系(回顾)探索:从一块三角形材料中,能否剪下一个圆,使其与各边都相切?I●I●上右图就是三角形的内切圆作法:D (1)作∠ABC、∠ACB的平分线BM和CN,交点为I.
(2)过点I作ID⊥BC,垂足为D.
(3)以I为圆心,ID为半径作⊙I, ⊙I就是所求MN这样的圆可以作出几个呢?为什么?∵直线BE和CF只有一个交点I,并且点I到△ABC三边的距离相等(为什么?),因此和△ABC三边都相切的圆可以作出一个,并且只能作一个. 定义:
与三角形三边都相切的圆叫做三角形的内切圆.这个三角形叫做圆的外切三角形.
内切圆的圆心叫做三角形的内心,是三角形三条角平分线的交点. 分别作出锐角三角形,直角三角形,钝角三角形的内切圆,并说明与它们内心的位置情况?提示:先确定圆心和半径,尺规作图要保留作图痕迹. 判断题:
1.三角形的内心到三角形各个顶点的距离相等。( )
2.三角形的外心到三角形各边的距离相等。( )
3.等边三角形的内心和外心重( )错错对4、三角形的内心一定在三角形的内部( )
5、菱形一定有内切圆( )
6、矩形一定有内切圆( )
对 错 对
例2:如图,在△ABC中,点O是内心,
(1)若∠ABC=50°,∠ACB=70°,求∠BOC的度数(2)若∠A=80度,则∠BOC=
(3)若∠BOC=110度,则∠A= 130401。已知:如图,⊙O是Rt△ABC的内切圆,∠C是直角,∠AC=3,BC=4.
求⊙O的半径r. ABC●┏O Rt△的三边长与其内切圆半径间的关系bac已知:如图,△ABC的面积S=4cm2,周长等于10cm.
求内切圆⊙O的半径r.斜△的三边长及面积与其内切圆半径间的关系思考题:
如图,某乡镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑,以树立起文明古镇的形象。已知雕塑中心M到道路三边AC、BC、AB的距离相等,AC⊥BC,BC=30米,AC=40米。请你帮助计算一下,镇标雕塑中心M离道路三边的距离有多远?谢谢
