1.2二次函数的图象与性质(第1课时)课件(共13张ppt)
文档属性
| 名称 | 1.2二次函数的图象与性质(第1课时)课件(共13张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 507.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-24 00:00:00 | ||
图片预览


文档简介
课件10张PPT。一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函
数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表
达式的二次项系数、一次项系数和常数项.2、二次函数满足的条件
(1)自变量x的最高次数为二次
(2)二次项系数不等于0
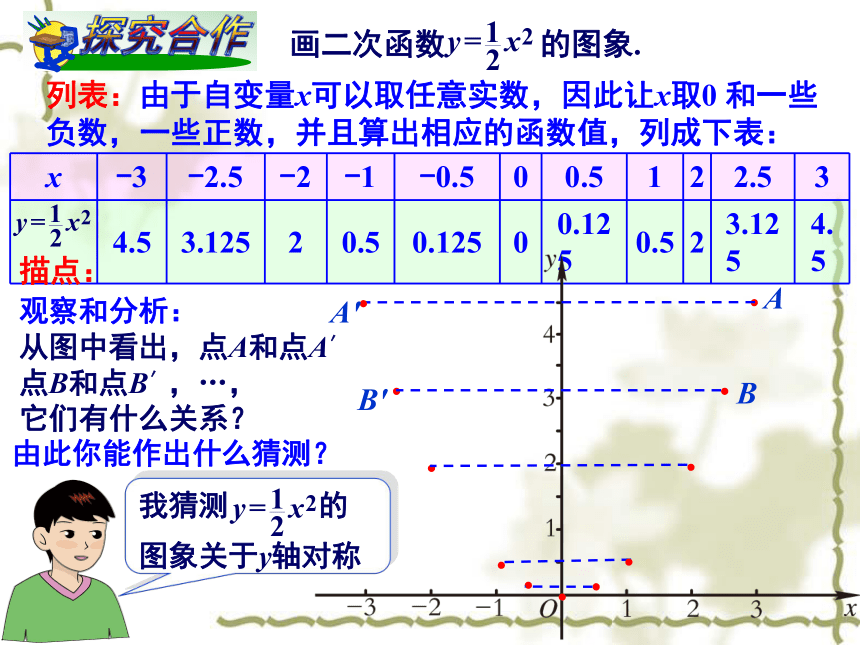
(3)函数的右边是一个整式1、二次函数的定义:3、描点法画函数图像的步骤:列表:根据函数的解析式,把自变量取值和对应的
函数值列一个表。描点:把自变量取值和对应的函数值看作一个点的坐标。连线:把所描出的点,用平滑的直线(曲线)连起来。列表:由于自变量x可以取任意实数,因此让x取0 和一些负数,一些正数,并且算出相应的函数值,列成下表:描点:观察和分析:
从图中看出,点A和点A′
点B和点B′,…,
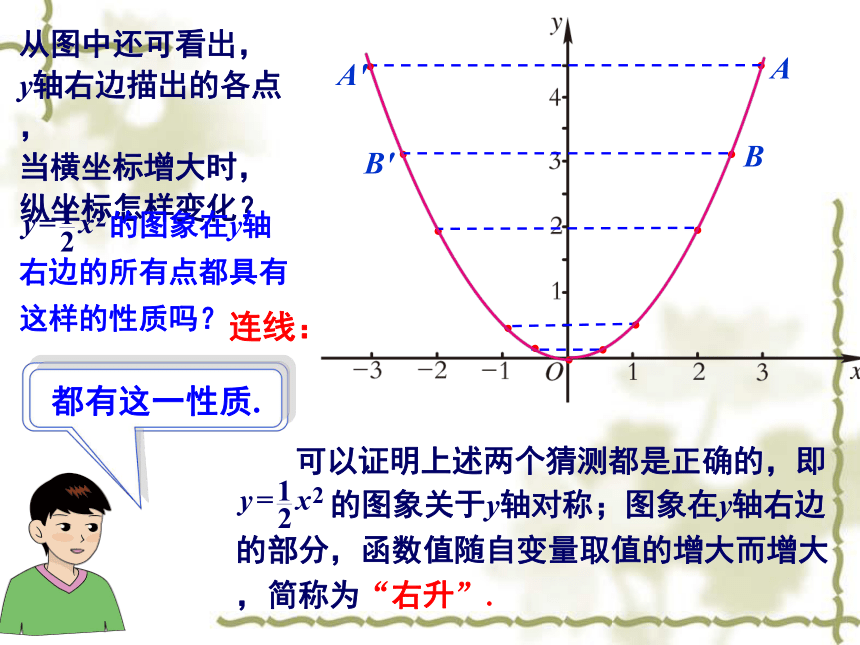
它们有什么关系?AA'BB'由此你能作出什么猜测?AA'BB'从图中还可看出,
y轴右边描出的各点,
当横坐标增大时,
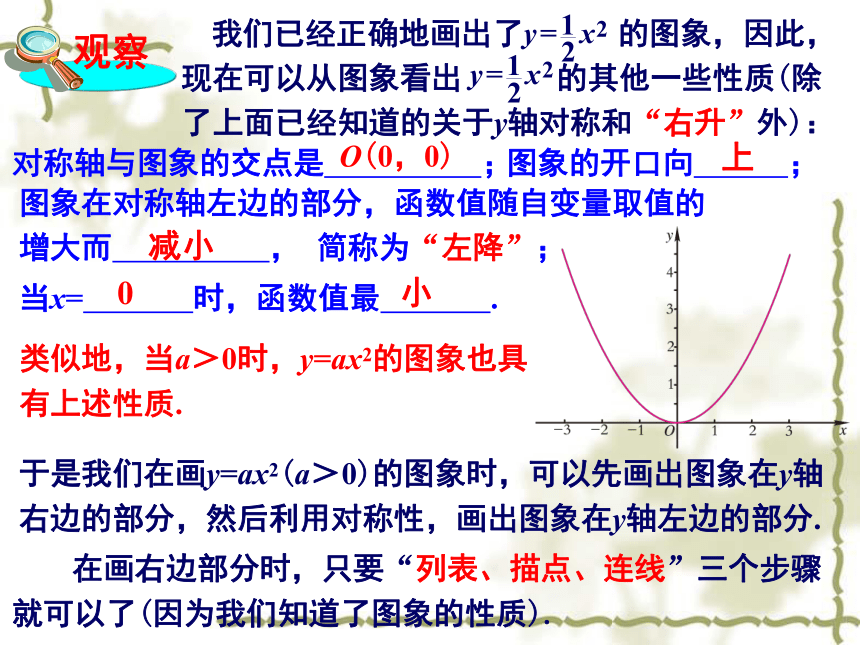
纵坐标怎样变化?纵坐标随着增大.都有这一性质.连线:对称轴与图象的交点是 ;图象的开口向 ;图象在对称轴左边的部分,函数值随自变量取值的增大而 , 简称为“左降”;当x= 时,函数值最 .O(0,0)上减小0小类似地,当a>0时,y=ax2的图象也具有上述性质.于是我们在画y=ax2(a>0)的图象时,可以先画出图象在y轴右边的部分,然后利用对称性,画出图象在y轴左边的部分. 在画右边部分时,只要“列表、描点、连线”三个步骤就可以了(因为我们知道了图象的性质).例1 画二次函数y=x2的图象.列表:描点和连线:画出图象在y轴右边的部分. 如图 利用对称性,画出图象在y轴左边的部分.这样我们得到了y=x2的图象.如图1. 二次函数y=6x2的性质有:(1)对称轴是 ;(2)图象的开口向 ;(3)图象在对称轴右边的部分,函数值随自变量取值的增大而 ;在对称轴左边的部分,函数值随自变量取值的增大而 .x = 0上增大减小k=2y=4x2对称轴是y轴。或:直线x=0(0,0)5、已知二次函数y=ax2的图像经过点A(2,8)
(1)求此函数解析式;
(2)判断点B(1,4)是否在此函数图像上;
(3)求出此函数图像上纵坐标为18的点的坐标。解:(1)把A(2,8)代人y=ax2∴ a=2∴ y=2x2(2) 当x=1时,y=2 ≠ 4∴ B(1,4)不在y=2x2的图像上。(3) 当y=18时,即2x2=18,x=3或x=-3∴ 纵坐标是18的点是:(3,18)和(-3,18)对称轴与图象的交点是 ;图象的开口向 ;图象在对称轴右边的部分,函数值随自变量取值的增大而 , 简称为“右升”;当x= 时,函数值最 .O(0,0)上减小0小对于y=ax2(当a>0时)的图象也具有上述性质.图象是轴对称图形,对称轴是_______图象在对称轴左边的部分,函数值随
自变量取值的增大而 ,
简称为“左降”;y轴增大x=0
数叫做x的二次函数.其中,是x自变量,a,b,c分别是函数表
达式的二次项系数、一次项系数和常数项.2、二次函数满足的条件
(1)自变量x的最高次数为二次
(2)二次项系数不等于0
(3)函数的右边是一个整式1、二次函数的定义:3、描点法画函数图像的步骤:列表:根据函数的解析式,把自变量取值和对应的
函数值列一个表。描点:把自变量取值和对应的函数值看作一个点的坐标。连线:把所描出的点,用平滑的直线(曲线)连起来。列表:由于自变量x可以取任意实数,因此让x取0 和一些负数,一些正数,并且算出相应的函数值,列成下表:描点:观察和分析:
从图中看出,点A和点A′
点B和点B′,…,
它们有什么关系?AA'BB'由此你能作出什么猜测?AA'BB'从图中还可看出,
y轴右边描出的各点,
当横坐标增大时,
纵坐标怎样变化?纵坐标随着增大.都有这一性质.连线:对称轴与图象的交点是 ;图象的开口向 ;图象在对称轴左边的部分,函数值随自变量取值的增大而 , 简称为“左降”;当x= 时,函数值最 .O(0,0)上减小0小类似地,当a>0时,y=ax2的图象也具有上述性质.于是我们在画y=ax2(a>0)的图象时,可以先画出图象在y轴右边的部分,然后利用对称性,画出图象在y轴左边的部分. 在画右边部分时,只要“列表、描点、连线”三个步骤就可以了(因为我们知道了图象的性质).例1 画二次函数y=x2的图象.列表:描点和连线:画出图象在y轴右边的部分. 如图 利用对称性,画出图象在y轴左边的部分.这样我们得到了y=x2的图象.如图1. 二次函数y=6x2的性质有:(1)对称轴是 ;(2)图象的开口向 ;(3)图象在对称轴右边的部分,函数值随自变量取值的增大而 ;在对称轴左边的部分,函数值随自变量取值的增大而 .x = 0上增大减小k=2y=4x2对称轴是y轴。或:直线x=0(0,0)5、已知二次函数y=ax2的图像经过点A(2,8)
(1)求此函数解析式;
(2)判断点B(1,4)是否在此函数图像上;
(3)求出此函数图像上纵坐标为18的点的坐标。解:(1)把A(2,8)代人y=ax2∴ a=2∴ y=2x2(2) 当x=1时,y=2 ≠ 4∴ B(1,4)不在y=2x2的图像上。(3) 当y=18时,即2x2=18,x=3或x=-3∴ 纵坐标是18的点是:(3,18)和(-3,18)对称轴与图象的交点是 ;图象的开口向 ;图象在对称轴右边的部分,函数值随自变量取值的增大而 , 简称为“右升”;当x= 时,函数值最 .O(0,0)上减小0小对于y=ax2(当a>0时)的图象也具有上述性质.图象是轴对称图形,对称轴是_______图象在对称轴左边的部分,函数值随
自变量取值的增大而 ,
简称为“左降”;y轴增大x=0
