1.2二次函数的图象与性质(第2课时)课件(共11张ppt)
文档属性
| 名称 | 1.2二次函数的图象与性质(第2课时)课件(共11张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-25 00:00:00 | ||
图片预览

文档简介
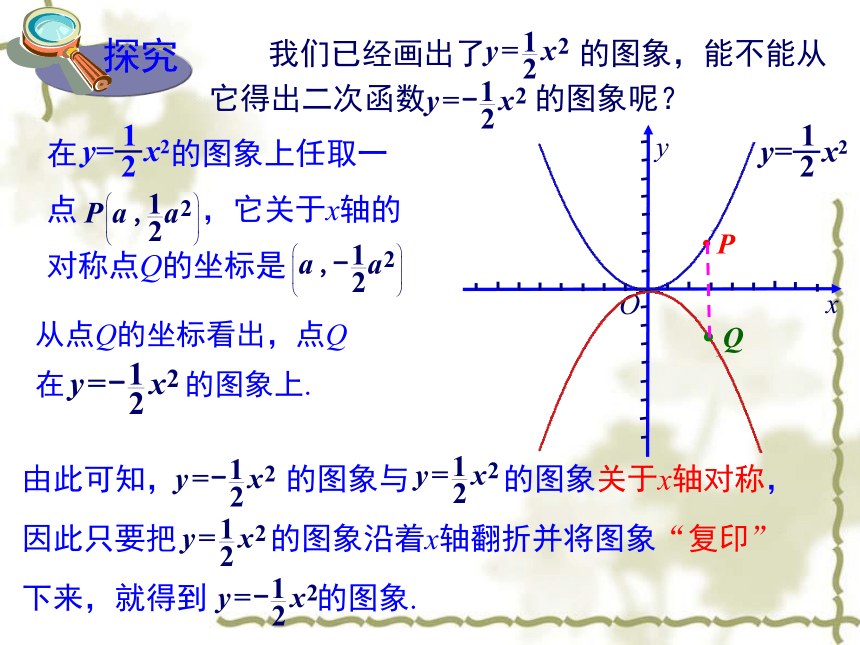
课件11张PPT。湘教版SHUXUE九年级下二次函数的图像与性质(2)对称轴与图象的交点是 ;图象的开口向 ;图象在对称轴右边的部分,函数值随自变量取值的增大而 , 简称为“右升”;当x= 时,函数值最 .O(0,0)上减小0小对于y=ax2(当a>0时)的图象也具有上述性质.图象是轴对称图形,对称轴是_______图象在对称轴左边的部分,函数值随
自变量取值的增大而 ,
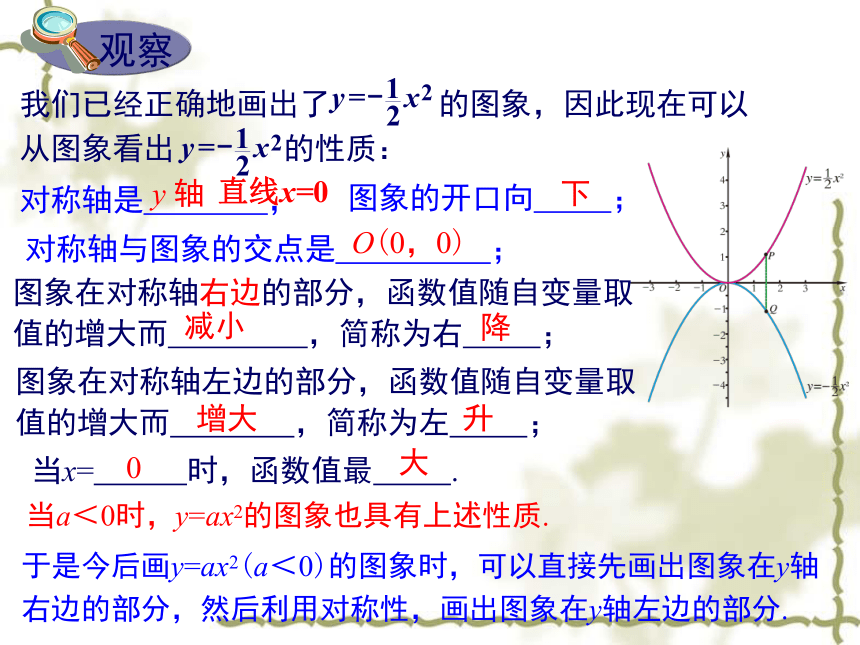
简称为“左降”;y轴增大x=0 我们已经画出了 的图象,能不能从它得出二次函数 的图象呢?从点Q的坐标看出,点Q在 的图象上.由此可知, 的图象与 的图象关于x轴对称,因此只要把 的图象沿着x轴翻折并将图象“复印”下来,就得到 的图象. 我们已经正确地画出了 的图象,因此现在可以从图象看出 的性质:对称轴是 ,对称轴与图象的交点是 ;图象的开口向 ;y 轴O(0,0)下直线x=0图象在对称轴右边的部分,函数值随自变量取值的增大而 ,简称为右 ;减小降图象在对称轴左边的部分,函数值随自变量取值的增大而 ,简称为左 ;增大升当x= 时,函数值最 .0大当a<0时,y=ax2的图象也具有上述性质.于是今后画y=ax2(a<0)的图象时,可以直接先画出图象在y轴右边的部分,然后利用对称性,画出图象在y轴左边的部分.举
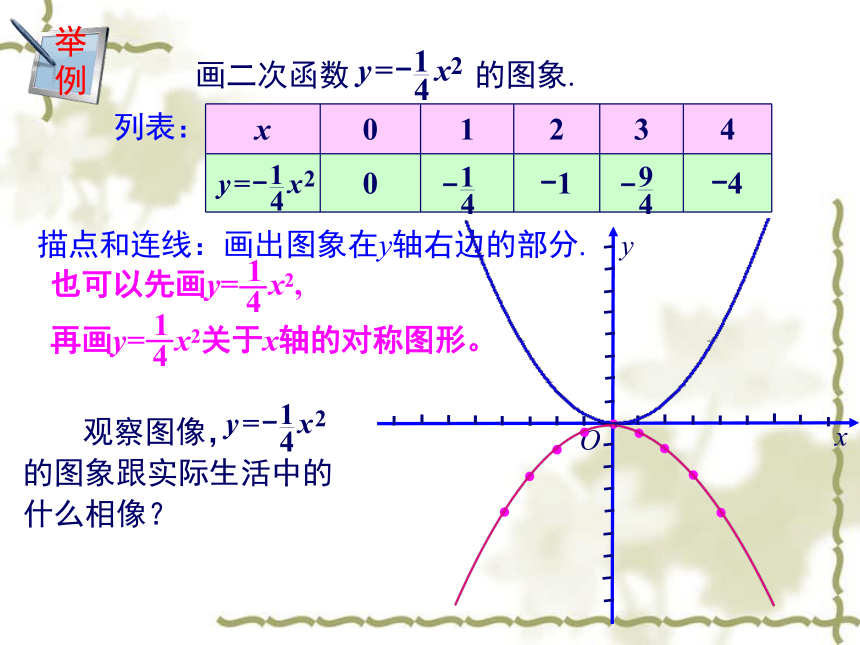
例 画二次函数 的图象. 列表:描点和连线:画出图象在y轴右边的部分. 观察图像, 的图象跟实际生活中的什么相像? 的图象很像掷铅球时,铅球在空中经过的路线.以铅球在空中经过的路线的最高点
为原点建立直角坐标系,x轴的正向水平向右,y轴的正向竖直向上,则可以求出铅球在空中经过的路线是形式为y=ax2(a<0)的图象的一段,由此受到启发,我们引进下述概念: 一般地,二次函数y=ax2的图象叫做抛物线. 二次函数y=ax2的图象关于y轴对称. 抛物线与它的对称轴的交点叫做抛物线的顶点. 抛物线y=ax2的顶点是原点.1. 画出二次函数y=-x2 的图象.2. 二次函数y=-10x2的性质有:(1)对称轴是 ,
顶点是 ;y轴原点O(0,0)(2)图象的开口向 ;下(3)抛物线在对称轴右边的部分,函数值随自变量取值的增大而 ;在对称轴左边的部分,函数值随自变量取值的增大而 .减小增大直线x=0与上节课y=x2比较它们有什么相同和不同?3、物体从某一高度落下,已知下落的高度h(m)和下落的时间t(s)的关系是:h=4.9t2,h是t的 函数,它的图象的顶点坐标是 .(0,0)二次4.若抛物线y=ax2 (a ≠ 0),过点(-1,3)。
(1)则a的值是 ;
(2)对称轴是 ,开口 。
(3)顶点坐标是 ,顶点是抛物线上的 。抛物线在x轴的 方(除顶点外)。3y轴向上(0,0)最低点上︱a︱越大,函数图像的开口越窄,函数图象越陡6. 在同一直角坐标系中,分别画出函数 y=-0.3x2与
y=-8x2的图象,并分别说出 它们的共同点和不同点.C②③⑥①④⑤⑤9、求抛物线y=x2与直线y=x-6的交点坐标。10、已知二次函数y=-x2
利用图像解答下列问题:
(1)当-2 (2)当-4(除顶点外)向上向下当x=0时,
最小值为0。二次函数y=ax2的性质y轴(直线x=0)(0,0)在x轴的下方
(除顶点外)当x=0时,
最大值为0。
自变量取值的增大而 ,
简称为“左降”;y轴增大x=0 我们已经画出了 的图象,能不能从它得出二次函数 的图象呢?从点Q的坐标看出,点Q在 的图象上.由此可知, 的图象与 的图象关于x轴对称,因此只要把 的图象沿着x轴翻折并将图象“复印”下来,就得到 的图象. 我们已经正确地画出了 的图象,因此现在可以从图象看出 的性质:对称轴是 ,对称轴与图象的交点是 ;图象的开口向 ;y 轴O(0,0)下直线x=0图象在对称轴右边的部分,函数值随自变量取值的增大而 ,简称为右 ;减小降图象在对称轴左边的部分,函数值随自变量取值的增大而 ,简称为左 ;增大升当x= 时,函数值最 .0大当a<0时,y=ax2的图象也具有上述性质.于是今后画y=ax2(a<0)的图象时,可以直接先画出图象在y轴右边的部分,然后利用对称性,画出图象在y轴左边的部分.举
例 画二次函数 的图象. 列表:描点和连线:画出图象在y轴右边的部分. 观察图像, 的图象跟实际生活中的什么相像? 的图象很像掷铅球时,铅球在空中经过的路线.以铅球在空中经过的路线的最高点
为原点建立直角坐标系,x轴的正向水平向右,y轴的正向竖直向上,则可以求出铅球在空中经过的路线是形式为y=ax2(a<0)的图象的一段,由此受到启发,我们引进下述概念: 一般地,二次函数y=ax2的图象叫做抛物线. 二次函数y=ax2的图象关于y轴对称. 抛物线与它的对称轴的交点叫做抛物线的顶点. 抛物线y=ax2的顶点是原点.1. 画出二次函数y=-x2 的图象.2. 二次函数y=-10x2的性质有:(1)对称轴是 ,
顶点是 ;y轴原点O(0,0)(2)图象的开口向 ;下(3)抛物线在对称轴右边的部分,函数值随自变量取值的增大而 ;在对称轴左边的部分,函数值随自变量取值的增大而 .减小增大直线x=0与上节课y=x2比较它们有什么相同和不同?3、物体从某一高度落下,已知下落的高度h(m)和下落的时间t(s)的关系是:h=4.9t2,h是t的 函数,它的图象的顶点坐标是 .(0,0)二次4.若抛物线y=ax2 (a ≠ 0),过点(-1,3)。
(1)则a的值是 ;
(2)对称轴是 ,开口 。
(3)顶点坐标是 ,顶点是抛物线上的 。抛物线在x轴的 方(除顶点外)。3y轴向上(0,0)最低点上︱a︱越大,函数图像的开口越窄,函数图象越陡6. 在同一直角坐标系中,分别画出函数 y=-0.3x2与
y=-8x2的图象,并分别说出 它们的共同点和不同点.C②③⑥①④⑤⑤9、求抛物线y=x2与直线y=x-6的交点坐标。10、已知二次函数y=-x2
利用图像解答下列问题:
(1)当-2
最小值为0。二次函数y=ax2的性质y轴(直线x=0)(0,0)在x轴的下方
(除顶点外)当x=0时,
最大值为0。
