第一章二次函数(第1课时)复习课件(共12张ppt)
文档属性
| 名称 | 第一章二次函数(第1课时)复习课件(共12张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 101.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-25 00:00:00 | ||
图片预览




文档简介
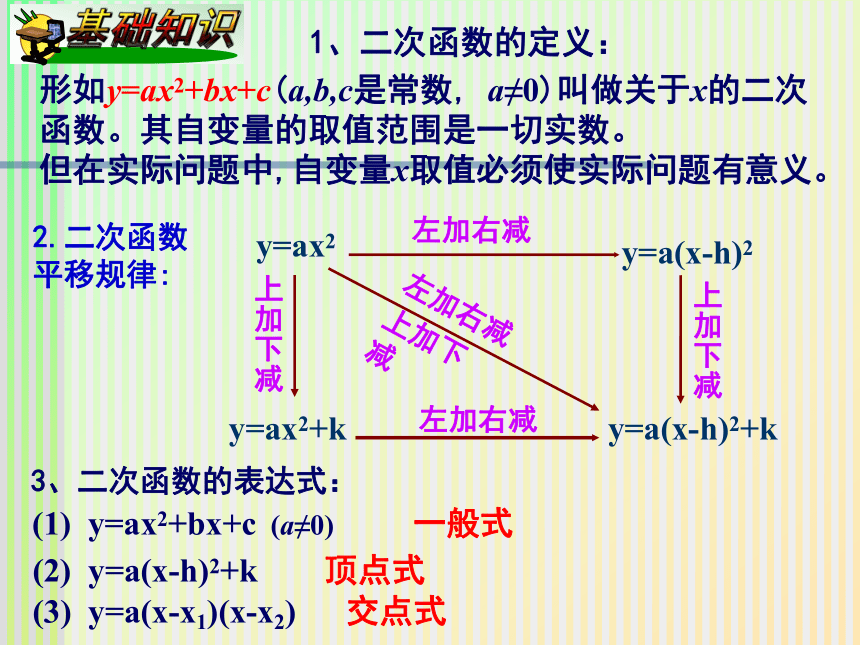
课件12张PPT。形如y=ax2+bx+c(a,b,c是常数, a≠0)叫做关于x的二次函数。其自变量的取值范围是一切实数。
但在实际问题中,自变量x取值必须使实际问题有意义。2.二次函数平移规律: y=ax2y=ax2+ky=a(x-h)2y=a(x-h)2+k1、二次函数的定义:3、二次函数的表达式:(1) y=ax2+bx+c (a≠0) 一般式(2) y=a(x-h)2+k 顶点式(3) y=a(x-x1)(x-x2) 交点式y=ax2+bx+c的性质向上向下y有最小值y有最大值左降右升左升右降将解析式配方得:y=a(x-h)2+k的形式,叙述其性质:1.当y=-x2+3x+m-1的图像过原点,m值为( )
A -1 B 3 C 1 D -32.若y=ax2+bx的图像经过原点和第二,三,四象限,则( )
A a>0,b<0 B a>0,b>0
C a<0 ,b>0 D a<0 , b<0 CDD一、选择题4.若点(3,6),(7,6)是二次函数y=ax2+bx+c(a≠0)图像上两个点,则它的对称轴是( )
A x=-4 B x=4 C x=5 D x=6C5.若二次函数的对称轴是y 轴,且在y轴上的截距是c(c≠0) 则解析式是( )
A. y=ax2+bx+c(a≠0, b≠0) B. y=ax2+c(a≠0)
C .y=ax2+bx(a≠0 b≠0) D. y=ax2(a≠0) B6.已知抛物线y=ax2+bx+c与x轴的负半轴有两个交点,且a<0,那么抛物线的顶点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限B7.若把抛物线y=x2+bx+c向左平移2个单位,再向上平
移3个单位,得抛物线y = x2 - 2x+1,则( )
A. b=2 B. b= -6 , c= 6
C. b=-8 D. b=-8 , c= 18 B8.抛物线y=2x2+8x-11的顶点在 ( )
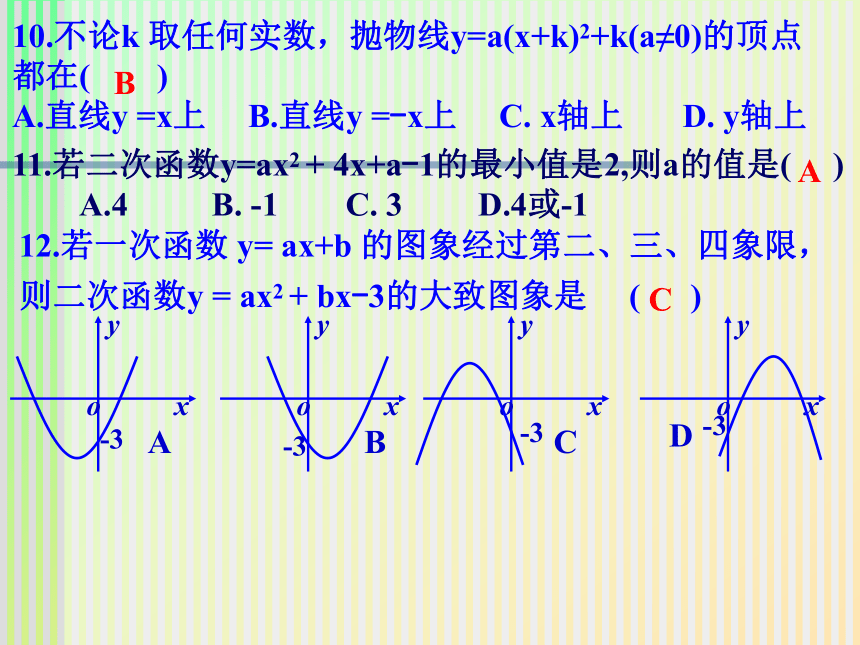
A.第一象限 B.第二象限 C.第三象限 D.第四象限CD9.在同一直角坐标系内,函数y=ax2+bx与y=ax+b(a,b≠0) 的大致图像( )10.不论k 取任何实数,抛物线y=a(x+k)2+k(a≠0)的顶点都在( )
A.直线y =x上 B.直线y =-x上 C. x轴上 D. y轴上B11.若二次函数y=ax2 + 4x+a-1的最小值是2,则a的值是( )
A.4 B. -1 C. 3 D.4或-1AC1.抛物线y=-x2-2x+3的开口向 ,对称轴是 ,
顶点坐标是 ,当x= 时,y有最 值
是 。当x 时,y随x的增大而增大,当x 时,y随x的增大而减小。下x=-1(-1,4)-1大4<-1>-12.二次函数y=(m-2)x2-3x+4-m2的图象经过原点,
则m= ____。-23.已知二次函数y=-3(x-2)2+4的图像绕顶点旋转180°,再向上平移2个单位后所得图像的函数解析式____________.y=3(x-2)2+64.已知抛物线y=x2-8x+c 的顶点在 x轴上,则c=____.165.若y=ax2+bx+c(a ? 0)与轴交于点A(2,0), B(4,0),
则对称轴是_____ ,顶点纵坐标是4,则抛物线的
解析式是 。 直线x=3y=-4x2+24x-32二、填空题6.二次函数y=x2-4x-5的图像与x轴的交点A(m,0),B(n,0)
(m0,c>0,则它的图像顶点在第________象限一10.已知二次函数图像顶点(1,-2),且形状与抛物线
y=-x2+2相同,则二次函数解析式___________y=-(x-1)2-2(4).已知二次函数的图象的对称轴是直线x=3,并且经过点(6,0),和(2,12)(2).已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2)。三、解答题:(6).已知二次函数的图象与x轴交于(-1,0)和(6,0),
并且经过点(2,12)(3).抛物线的顶点坐标是(6,-2),且与x轴的一个
交点的横坐标是8。 (5).抛物线经过点(4,-3),且x=3时y的最大值是4。1.确定下列函数表达式: (1).抛物线经过(2,0)(0,-2)(-2,3)三点。3、如图直线l经过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图像在第一象限内相交于P点,若△AOP的
面积为6,求二次函数的解析式.A(4,0),B(0,4)得直线AB的解析式为 y=-x+4,作PE⊥OA于E, 则 0.5OA×PE=6,
可得PE=3∴ P(1,3)∴ y=3x2 x1+x2=1m=-2y=5x2-5x-2提示:由对称轴和A(-1,0),得B(3,0)设解析式为:y=a(x+1)(x-3)AB=4=-(m-1)2+4当P(1,2),△ABP的最大面积是4提示:在Rt△AOC中,由条件得:OC=3,OA=4
在Rt△AOB中,OB=1 ∴ A(0,4)、B(-1,0)、C(3,0)设函数解析式是y=ax2+bx+c抛物线开口向下,当x<1时,
y随x增大而增大。(2)求经过A,B,C三点的二次函数解析式(3)写出二次函数的对称轴,顶点坐标(4)当y随x的增大而增大时,x的取值范围
但在实际问题中,自变量x取值必须使实际问题有意义。2.二次函数平移规律: y=ax2y=ax2+ky=a(x-h)2y=a(x-h)2+k1、二次函数的定义:3、二次函数的表达式:(1) y=ax2+bx+c (a≠0) 一般式(2) y=a(x-h)2+k 顶点式(3) y=a(x-x1)(x-x2) 交点式y=ax2+bx+c的性质向上向下y有最小值y有最大值左降右升左升右降将解析式配方得:y=a(x-h)2+k的形式,叙述其性质:1.当y=-x2+3x+m-1的图像过原点,m值为( )
A -1 B 3 C 1 D -32.若y=ax2+bx的图像经过原点和第二,三,四象限,则( )
A a>0,b<0 B a>0,b>0
C a<0 ,b>0 D a<0 , b<0 CDD一、选择题4.若点(3,6),(7,6)是二次函数y=ax2+bx+c(a≠0)图像上两个点,则它的对称轴是( )
A x=-4 B x=4 C x=5 D x=6C5.若二次函数的对称轴是y 轴,且在y轴上的截距是c(c≠0) 则解析式是( )
A. y=ax2+bx+c(a≠0, b≠0) B. y=ax2+c(a≠0)
C .y=ax2+bx(a≠0 b≠0) D. y=ax2(a≠0) B6.已知抛物线y=ax2+bx+c与x轴的负半轴有两个交点,且a<0,那么抛物线的顶点在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限B7.若把抛物线y=x2+bx+c向左平移2个单位,再向上平
移3个单位,得抛物线y = x2 - 2x+1,则( )
A. b=2 B. b= -6 , c= 6
C. b=-8 D. b=-8 , c= 18 B8.抛物线y=2x2+8x-11的顶点在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限CD9.在同一直角坐标系内,函数y=ax2+bx与y=ax+b(a,b≠0) 的大致图像( )10.不论k 取任何实数,抛物线y=a(x+k)2+k(a≠0)的顶点都在( )
A.直线y =x上 B.直线y =-x上 C. x轴上 D. y轴上B11.若二次函数y=ax2 + 4x+a-1的最小值是2,则a的值是( )
A.4 B. -1 C. 3 D.4或-1AC1.抛物线y=-x2-2x+3的开口向 ,对称轴是 ,
顶点坐标是 ,当x= 时,y有最 值
是 。当x 时,y随x的增大而增大,当x 时,y随x的增大而减小。下x=-1(-1,4)-1大4<-1>-12.二次函数y=(m-2)x2-3x+4-m2的图象经过原点,
则m= ____。-23.已知二次函数y=-3(x-2)2+4的图像绕顶点旋转180°,再向上平移2个单位后所得图像的函数解析式____________.y=3(x-2)2+64.已知抛物线y=x2-8x+c 的顶点在 x轴上,则c=____.165.若y=ax2+bx+c(a ? 0)与轴交于点A(2,0), B(4,0),
则对称轴是_____ ,顶点纵坐标是4,则抛物线的
解析式是 。 直线x=3y=-4x2+24x-32二、填空题6.二次函数y=x2-4x-5的图像与x轴的交点A(m,0),B(n,0)
(m
y=-x2+2相同,则二次函数解析式___________y=-(x-1)2-2(4).已知二次函数的图象的对称轴是直线x=3,并且经过点(6,0),和(2,12)(2).已知二次函数的图象的顶点坐标为(-2,-3),且图象过点(-3,-2)。三、解答题:(6).已知二次函数的图象与x轴交于(-1,0)和(6,0),
并且经过点(2,12)(3).抛物线的顶点坐标是(6,-2),且与x轴的一个
交点的横坐标是8。 (5).抛物线经过点(4,-3),且x=3时y的最大值是4。1.确定下列函数表达式: (1).抛物线经过(2,0)(0,-2)(-2,3)三点。3、如图直线l经过点A(4,0)和B(0,4)两点,它与二次函数y=ax2的图像在第一象限内相交于P点,若△AOP的
面积为6,求二次函数的解析式.A(4,0),B(0,4)得直线AB的解析式为 y=-x+4,作PE⊥OA于E, 则 0.5OA×PE=6,
可得PE=3∴ P(1,3)∴ y=3x2 x1+x2=1m=-2y=5x2-5x-2提示:由对称轴和A(-1,0),得B(3,0)设解析式为:y=a(x+1)(x-3)AB=4=-(m-1)2+4当P(1,2),△ABP的最大面积是4提示:在Rt△AOC中,由条件得:OC=3,OA=4
在Rt△AOB中,OB=1 ∴ A(0,4)、B(-1,0)、C(3,0)设函数解析式是y=ax2+bx+c抛物线开口向下,当x<1时,
y随x增大而增大。(2)求经过A,B,C三点的二次函数解析式(3)写出二次函数的对称轴,顶点坐标(4)当y随x的增大而增大时,x的取值范围
