九年级下2.3垂径定理(第1课时)课件
图片预览


文档简介
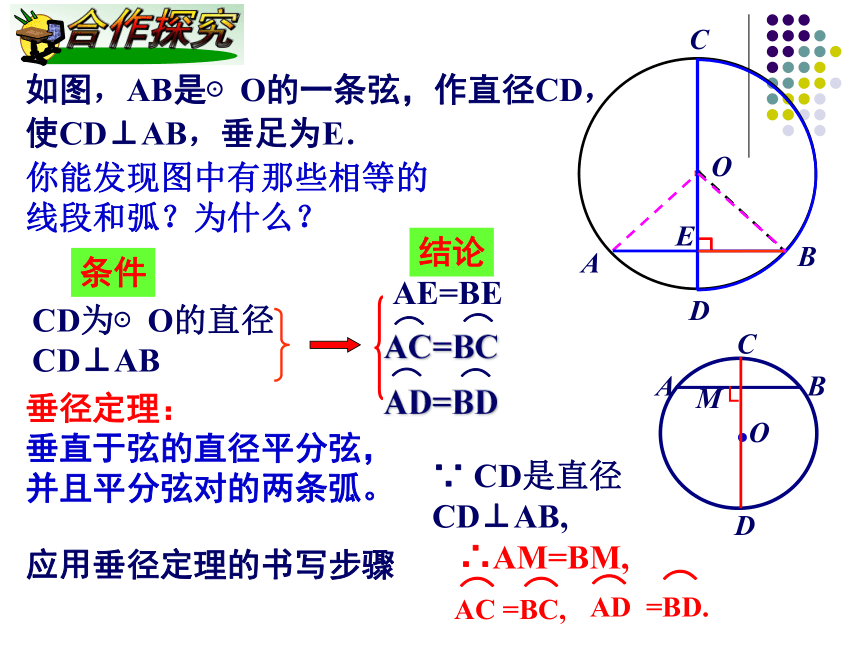
课件9张PPT。垂径定理(1)垂直于弦的直径-------1、什么叫轴对称图形?2、圆是轴对称图形吗?如果是,它的对称轴是什么?圆是轴对称图形,其对称轴是任意一条直径(过圆心的直线)。 1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).如图,AB是⊙O的一条弦,作直径CD,
使CD⊥AB,垂足为E.你能发现图中有那些相等的
线段和弧?为什么?CD为⊙O的直径
CD⊥AB 条件结论AE=BE垂径定理:
垂直于弦的直径平分弦,
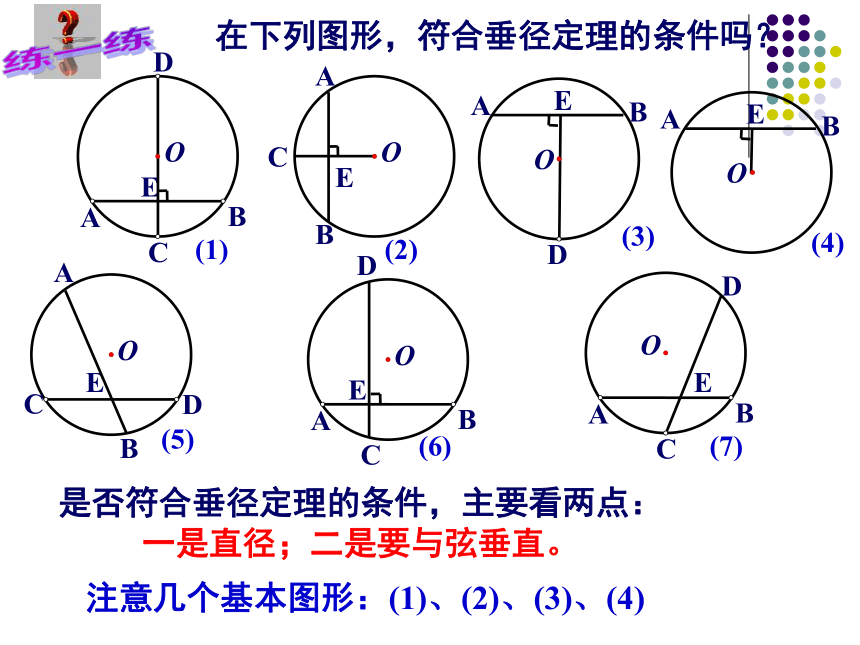
并且平分弦对的两条弧。应用垂径定理的书写步骤∵ CD是直径 CD⊥AB,∴AM=BM,在下列图形,符合垂径定理的条件吗?是否符合垂径定理的条件,主要看两点:
一是直径;二是要与弦垂直。注意几个基本图形:(1)、(2)、(3)、(4) 例1 如图,已知在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。解:连结OA由勾股定理得:圆心到弦的距离、半径、弦的一半构成直角
三角形,便将问题转化为直角三角形的问题。
18.7R-7.2R解决“赵州桥”问题:如图,OA=OC=R,
OD=OC-CD=R-7.2 AB=18.7AD2+OD2=OA2即:18.72+(R-7.2)2=R2R≈27.9(m)答:赵州桥的主桥拱半径约为27.9m.3、已知:如图所示,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。求证:AC=BD.∴AE=BE,CE=DEAE-CE=BE-DE∴AC=BD4、已知⊙O的半径为13cm,该圆的弦AB∥CD,且AB=10cm,CD=24cm,求弦AB和弦CD之间的距离。∴AB∥CD在Rt?OCE中,OE=5cm在Rt?OAF中,OF=12cm∴EF=OF-OE=7cm弦AB、CD在圆心两侧时,EF=OE+OF=17cm1.半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是 。2.⊙O的直径为10cm,圆心O到弦AB的
距离为3cm,则弦AB的长是 。8cm3.半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是 。4.弓形的弦长AB为24cm,弓形的高CD为8cm,则这弓形所在圆的半径为 . 13cm5、如图,AC⊥BO,AC=8cm,BA=5cm,
则⊙O的半径为 ,AC的弦心距为 。6、如图,AB是⊙O的弦,P是AB上一点,若AB=10cm,PB=4cm,OP=5cm,则⊙O的半径等于 cm。7、已知,M是⊙O内一点,已知过点M的
⊙O最长的弦为10cm,最短的弦长为8cm,
则OM=_____ cm. 8、在直径为650毫米的圆柱形油槽内装入一些油后,截面如图所示。若油面宽AB=600毫米,求油的最大深度。9、求证:同圆中,两平行弦所夹得弧相等。73请围绕以下两个方面小结本节课:1、从知识上学习了什么?垂径定理:垂直于弦的直径平分弦,并且平分弦对的两条弧。2、从方法上学习了什么?(1)垂径定理是圆中一个重要的结论,叙述语言要准确,一条直线只要满足①过圆心;②垂直于弦;则可得
③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧。(2)、垂径定理和勾股定理有机结合计算弦长、半径、弦心距等问题的方法,构造直角三角形 (3)解决有关弦的问题时,经常
①连结半径;
②过圆心作一条与弦垂直的线段等辅助线,为应用垂径定理创造条件。
使CD⊥AB,垂足为E.你能发现图中有那些相等的
线段和弧?为什么?CD为⊙O的直径
CD⊥AB 条件结论AE=BE垂径定理:
垂直于弦的直径平分弦,
并且平分弦对的两条弧。应用垂径定理的书写步骤∵ CD是直径 CD⊥AB,∴AM=BM,在下列图形,符合垂径定理的条件吗?是否符合垂径定理的条件,主要看两点:
一是直径;二是要与弦垂直。注意几个基本图形:(1)、(2)、(3)、(4) 例1 如图,已知在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径。解:连结OA由勾股定理得:圆心到弦的距离、半径、弦的一半构成直角
三角形,便将问题转化为直角三角形的问题。
18.7R-7.2R解决“赵州桥”问题:如图,OA=OC=R,
OD=OC-CD=R-7.2 AB=18.7AD2+OD2=OA2即:18.72+(R-7.2)2=R2R≈27.9(m)答:赵州桥的主桥拱半径约为27.9m.3、已知:如图所示,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D两点。求证:AC=BD.∴AE=BE,CE=DEAE-CE=BE-DE∴AC=BD4、已知⊙O的半径为13cm,该圆的弦AB∥CD,且AB=10cm,CD=24cm,求弦AB和弦CD之间的距离。∴AB∥CD在Rt?OCE中,OE=5cm在Rt?OAF中,OF=12cm∴EF=OF-OE=7cm弦AB、CD在圆心两侧时,EF=OE+OF=17cm1.半径为4cm的⊙O中,弦AB=4cm,
那么圆心O到弦AB的距离是 。2.⊙O的直径为10cm,圆心O到弦AB的
距离为3cm,则弦AB的长是 。8cm3.半径为2cm的圆中,过半径中点且
垂直于这条半径的弦长是 。4.弓形的弦长AB为24cm,弓形的高CD为8cm,则这弓形所在圆的半径为 . 13cm5、如图,AC⊥BO,AC=8cm,BA=5cm,
则⊙O的半径为 ,AC的弦心距为 。6、如图,AB是⊙O的弦,P是AB上一点,若AB=10cm,PB=4cm,OP=5cm,则⊙O的半径等于 cm。7、已知,M是⊙O内一点,已知过点M的
⊙O最长的弦为10cm,最短的弦长为8cm,
则OM=_____ cm. 8、在直径为650毫米的圆柱形油槽内装入一些油后,截面如图所示。若油面宽AB=600毫米,求油的最大深度。9、求证:同圆中,两平行弦所夹得弧相等。73请围绕以下两个方面小结本节课:1、从知识上学习了什么?垂径定理:垂直于弦的直径平分弦,并且平分弦对的两条弧。2、从方法上学习了什么?(1)垂径定理是圆中一个重要的结论,叙述语言要准确,一条直线只要满足①过圆心;②垂直于弦;则可得
③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧。(2)、垂径定理和勾股定理有机结合计算弦长、半径、弦心距等问题的方法,构造直角三角形 (3)解决有关弦的问题时,经常
①连结半径;
②过圆心作一条与弦垂直的线段等辅助线,为应用垂径定理创造条件。
