九年级数学下2.3垂径定理(第2课时)课件
文档属性
| 名称 | 九年级数学下2.3垂径定理(第2课时)课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 251.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-12-25 13:51:44 | ||
图片预览



文档简介
课件12张PPT。湘教版SHUXUE九年级下垂径定理(2)垂直于弦的直径-------垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。 探究一、AB是⊙O的一条弦(非直径),
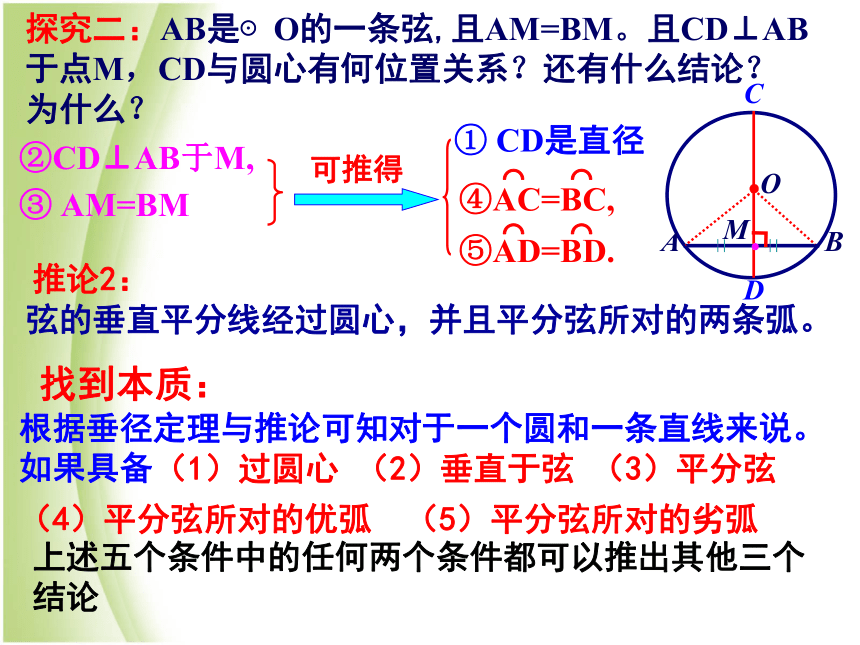
且AM=BM,过点M作直径CD.你发现图中有哪些等量关系?说说你的想法和理由.②CD⊥AB,由 ① CD是直径③ AM=BM·OABDC(E)(不是直径)连接OA,OB,则OA=OB.∴△OAM≌△OBM.∴∠AMO= ∠ BMO.∴CD⊥AB∵⊙O关于直径CD对称,探究二:AB是⊙O的一条弦,且AM=BM。且CD⊥AB
于点M,CD与圆心有何位置关系?还有什么结论?
为什么?②CD⊥AB于M, ① CD是直径③ AM=BM根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备 (1)过圆心 (2)垂直于弦 (3)平分弦
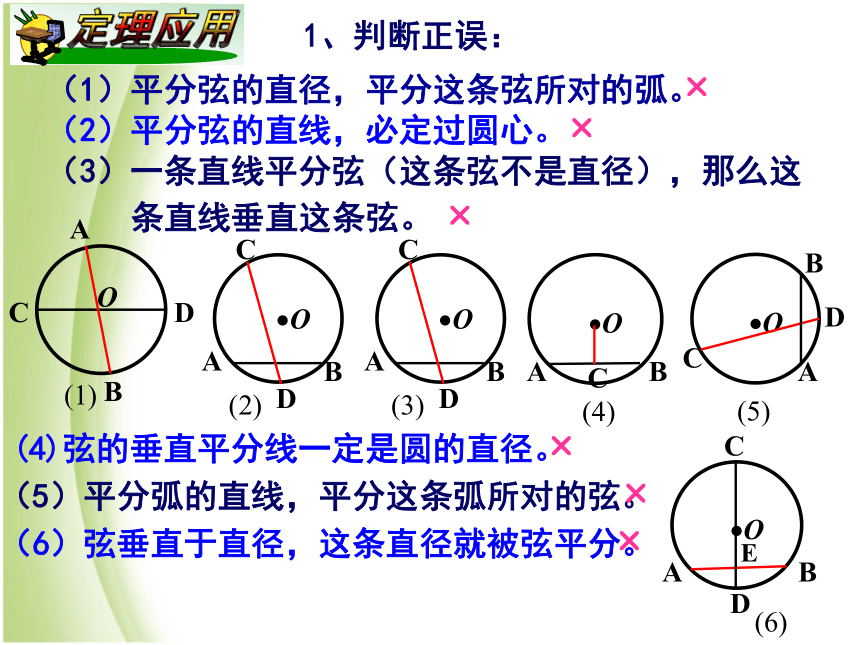
(4)平分弦所对的优弧 (5)平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论找到本质:1、判断正误:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。???(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的弦。(6)弦垂直于直径,这条直径就被弦平分。???2.已知A、B、C是⊙O上三点,且AB=AC,圆心O到
BC的距离为3厘米,圆的半径为5厘米,求AB长。3.如图,已知圆O的直径AB与弦CD相交于G,AE⊥CD于E,BF⊥CD于F,且圆O的半径为10㎝,CD=16 ㎝,求AE-BF的长。OD=3
OB=5BD=4AD=8解:连结OC,过点O作OM⊥CD于M,
则CM=MD∵CD=16,CM=8,
在Rt△OMC中,因OC=10∴OM=6∵AE⊥CD,BF⊥CD,OM⊥CD,∴AE∥OM∥BFAE-BF=2OM=124 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,
拱顶高出水面2.4米。现有一艘宽3米、船舱顶部为
长方形并高出水面2米的货船要经过这里,此货船能
顺利通过这座拱桥吗?如图,将问题转化为数学问题。AB=7.2,CD=2.4由垂径定理:AD=3.6HN=1.5设圆弧的半径OA为r,OD=r-2.4在Rt△OAD中,由勾股定理,得: r≈3.9(m)∴ DH=OH-OD=3.6-1.5=2.1>2∴此货船能顺利通过这座拱桥.1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的
两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所
对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦. ( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行.
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )2.已知:如图,⊙O 中,弦AB∥CD,AB<CD,
直径MN⊥AB,垂足为E,交弦CD于点F.
图中相等的线段有 : .
图中相等的劣弧有: .?√√?√AE=EBCF=FD3、如图,点P是半径为5cm的⊙O内一点,且OP=3cm,
则过P点的弦中,
(1)最长的弦= cm
(2)最短的弦= cm
(3)弦的长度为整数的共有( )
A、2条 B、3条 C、4条 D、5条C4、如图,⊙O的直径为10,弦AB=8,
P为AB上的一个动点,那么OP长
的取值范围是 。3cm≤OP≤5cm5、如图,点A、B是⊙O上两点,AB=8,
点P是⊙O上的动点(P与A、B不重合),
连接AP、BP,过点O分别作OE⊥AP于E,
OF⊥BP于F,EF= 。41086、已知⊙O的半径为5cm,弦AB的长
为8cm,求此弦的中点到这条弦所对
的弧的中点的距离。8、如图,CD为圆O的直径,弦AB交
CD于E,∠ CEB=30°,DE=9㎝,
CE=3㎝,求弦AB的长。DE=2cm8cm∠APC=∠COF=60°由条件:DC=12,OC=6,OE=OC-EC=3∠ CEB=30°=∠ FEO OF=1.59.如图,圆O与矩形ABCD交
于E、F、G、H,EF=10,
HG=6,AH=4,求BE的长.10、如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD求证:△OCD为等腰三角形。11、已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD,求证:EC=DFBE=2作OE⊥CD,AE=BE∵AC=BD∴CE=BE∴△OCE≌△ODE.∴OC=OD作OM⊥CD,∵AE⊥CD,BF⊥CD∴AE∥OM∥BF∵OA=OB,∴EM=MF∵CM=MD,∴EC=DF1、垂径定理及推论:对于一个圆和一条直线来说,如果具备 (1)过圆心 (2)垂直于弦 (3)平分弦
(4)平分弦所对的优弧 (5)平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论2、垂径定理及其推论和勾股定理相结合,方程的思想
来解决问题。drh对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:(1)r=d+h
且AM=BM,过点M作直径CD.你发现图中有哪些等量关系?说说你的想法和理由.②CD⊥AB,由 ① CD是直径③ AM=BM·OABDC(E)(不是直径)连接OA,OB,则OA=OB.∴△OAM≌△OBM.∴∠AMO= ∠ BMO.∴CD⊥AB∵⊙O关于直径CD对称,探究二:AB是⊙O的一条弦,且AM=BM。且CD⊥AB
于点M,CD与圆心有何位置关系?还有什么结论?
为什么?②CD⊥AB于M, ① CD是直径③ AM=BM根据垂径定理与推论可知对于一个圆和一条直线来说。如果具备 (1)过圆心 (2)垂直于弦 (3)平分弦
(4)平分弦所对的优弧 (5)平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论找到本质:1、判断正误:(1)平分弦的直径,平分这条弦所对的弧。(2)平分弦的直线,必定过圆心。(3)一条直线平分弦(这条弦不是直径),那么这
条直线垂直这条弦。???(4)弦的垂直平分线一定是圆的直径。(5)平分弧的直线,平分这条弧所对的弦。(6)弦垂直于直径,这条直径就被弦平分。???2.已知A、B、C是⊙O上三点,且AB=AC,圆心O到
BC的距离为3厘米,圆的半径为5厘米,求AB长。3.如图,已知圆O的直径AB与弦CD相交于G,AE⊥CD于E,BF⊥CD于F,且圆O的半径为10㎝,CD=16 ㎝,求AE-BF的长。OD=3
OB=5BD=4AD=8解:连结OC,过点O作OM⊥CD于M,
则CM=MD∵CD=16,CM=8,
在Rt△OMC中,因OC=10∴OM=6∵AE⊥CD,BF⊥CD,OM⊥CD,∴AE∥OM∥BFAE-BF=2OM=124 . 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,
拱顶高出水面2.4米。现有一艘宽3米、船舱顶部为
长方形并高出水面2米的货船要经过这里,此货船能
顺利通过这座拱桥吗?如图,将问题转化为数学问题。AB=7.2,CD=2.4由垂径定理:AD=3.6HN=1.5设圆弧的半径OA为r,OD=r-2.4在Rt△OAD中,由勾股定理,得: r≈3.9(m)∴ DH=OH-OD=3.6-1.5=2.1>2∴此货船能顺利通过这座拱桥.1、判断:
⑴垂直于弦的直线平分这条弦,并且平分弦所对的
两条弧. ( )
⑵平分弦所对的一条弧的直径一定平分这条弦所
对的另一条弧. ( )
⑶经过弦的中点的直径一定垂直于弦. ( )
⑷圆的两条弦所夹的弧相等,则这两条弦平行.
⑸弦的垂直平分线一定平分这条弦所对的弧. ( )2.已知:如图,⊙O 中,弦AB∥CD,AB<CD,
直径MN⊥AB,垂足为E,交弦CD于点F.
图中相等的线段有 : .
图中相等的劣弧有: .?√√?√AE=EBCF=FD3、如图,点P是半径为5cm的⊙O内一点,且OP=3cm,
则过P点的弦中,
(1)最长的弦= cm
(2)最短的弦= cm
(3)弦的长度为整数的共有( )
A、2条 B、3条 C、4条 D、5条C4、如图,⊙O的直径为10,弦AB=8,
P为AB上的一个动点,那么OP长
的取值范围是 。3cm≤OP≤5cm5、如图,点A、B是⊙O上两点,AB=8,
点P是⊙O上的动点(P与A、B不重合),
连接AP、BP,过点O分别作OE⊥AP于E,
OF⊥BP于F,EF= 。41086、已知⊙O的半径为5cm,弦AB的长
为8cm,求此弦的中点到这条弦所对
的弧的中点的距离。8、如图,CD为圆O的直径,弦AB交
CD于E,∠ CEB=30°,DE=9㎝,
CE=3㎝,求弦AB的长。DE=2cm8cm∠APC=∠COF=60°由条件:DC=12,OC=6,OE=OC-EC=3∠ CEB=30°=∠ FEO OF=1.59.如图,圆O与矩形ABCD交
于E、F、G、H,EF=10,
HG=6,AH=4,求BE的长.10、如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD求证:△OCD为等腰三角形。11、已知:AB是⊙O直径,CD是弦,AE⊥CD,BF⊥CD,求证:EC=DFBE=2作OE⊥CD,AE=BE∵AC=BD∴CE=BE∴△OCE≌△ODE.∴OC=OD作OM⊥CD,∵AE⊥CD,BF⊥CD∴AE∥OM∥BF∵OA=OB,∴EM=MF∵CM=MD,∴EC=DF1、垂径定理及推论:对于一个圆和一条直线来说,如果具备 (1)过圆心 (2)垂直于弦 (3)平分弦
(4)平分弦所对的优弧 (5)平分弦所对的劣弧上述五个条件中的任何两个条件都可以推出其他三个结论2、垂径定理及其推论和勾股定理相结合,方程的思想
来解决问题。drh对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:(1)r=d+h
